1. Introduction. In his set theory Zermelo uses the variables “x”, “y”, etc. for the representation of “things” generally. Among these things he includes sets, or, as I shall say henceforth, classes. He adopts the connective “ϵ” of membership as his sole special primitive; thus the elementary formulae of his system are describable simply as expressions of the form “xϵy”, with any thing-variables ”x”, “y”, “z”, etc. supplanting “x” and “y”. The postulates of his system are so fashioned as to avoid the logical paradoxes without use of the theory of types. One of the postulates, the so-called Aussonderungsaxiom, may be stated in familiar logical notation as

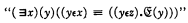
where 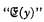is understood as any statement about y which is definite in a certain sense which Zermelo introduces informally for the purpose. Skolem has pointed out that it is adequate here to construe “definite” statements as embracing just the elementary formulae and all formulae thence constructible by the truth functions and by quantification with respect to thing-variables. A second of Zermelo's postulates is the principle of extensionality; this asserts that mutually inclusive classes are identical, i.e. are members of just the same classes. There are further postulates which provide for the existence of the null class, the class of all subclasses of any given class, the class of all members of members of any given class, the unit class of any given thing, and the class whose sole members are any two given things. Finally the multiplicative axiom (Auswahlprinzip) and the axiom of infinity are adopted.