We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
This journal utilises an Online Peer Review Service (OPRS) for submissions. By clicking "Continue" you will be taken to our partner site https://ef.msp.org/submit/asl_jsl. Please be aware that your Cambridge account is not valid for this OPRS and registration is required. We strongly advise you to read all "Author instructions" in the "Journal information" area prior to submitting.
Martin has shown that the notions of ancestral and class-inclusion are sufficient to develop the theory of natural numbers in a system containing variables of only one type.
The purpose of the present paper is to show that an analogous construction is possible in a system containing, beyond the quantificational level, only the ancestral and the ordered pair.
The formulae of our system comprise quantificational schemata and anything which can be obtained therefrom by writing pairs (e.g. (x; y), ((x; y); (x; (y; y))) etc.) for free variables, or by writing ancestral abstracts (e.g. (*xyFxy) etc.) for schematic letters, or both.
The ancestral abstract (*xyFxy) means what is usually meant by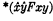 
; and the formula (*xyFxy)zw answers to Martin's (zw; xy)(Fxy).
The system presupposes a non-simple applied functional calculus of the first order, with a rule of substitution for predicate letters; over and above this it has three axioms for the ancestral and two for the ordered pair.