A topology on a set X is defined by specifying a family 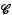 of its subsets which has the properties (i) arbitrary set intersections of members of
of its subsets which has the properties (i) arbitrary set intersections of members of 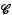 belong to
belong to 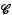 , (ii) finite set unions of members of
, (ii) finite set unions of members of 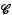 belong to
belong to 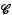 and (iii) the empty set □ and the set X each belong to
and (iii) the empty set □ and the set X each belong to 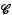 . The members of
. The members of 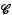 are called the closed subsets of X. If X is any subset of X then
are called the closed subsets of X. If X is any subset of X then 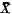 denotes the closure of X, that is, the set intersection of all closed subsets which contain X, however when X = {x} contains one point only we will denote
denotes the closure of X, that is, the set intersection of all closed subsets which contain X, however when X = {x} contains one point only we will denote 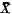 by
by 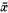 . The pair (X,
. The pair (X, 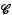 ) is called a topological space or, in what follows, a T-space. By a T-lattice we mean a complete distributive lattice of sets in which arbitrary g.l.b. means arbitrary set intersection, finite l.u.b. means finite set union and which contains the empty set □ It is well-known, for example Birkhoff [1], that if (X,
) is called a topological space or, in what follows, a T-space. By a T-lattice we mean a complete distributive lattice of sets in which arbitrary g.l.b. means arbitrary set intersection, finite l.u.b. means finite set union and which contains the empty set □ It is well-known, for example Birkhoff [1], that if (X, 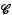 ) is a T-space and the members of
) is a T-space and the members of 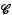 are partially ordered by set inclusion then
are partially ordered by set inclusion then 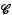 is a T-lattice.
is a T-lattice.