Published online by Cambridge University Press: 24 October 2008
A rubber molecule containing n + 1 carbon atoms may be represented by a chain of n links of equal length such that successive links are at a fixed angle to each other but are otherwise at random. The statistical distribution of the length of the molecule, that is, the distance between the first and last carbon atoms, has been considered by various authors (Treloar (1) gives references). In particular, if the first atom is kept fixed at the origin of a system of coordinates and the chain is otherwise at random, it has been conjectured that the distribution of the (n + 1)th atom will tend, as n increases, towards a three-dimensional normal distribution of the form
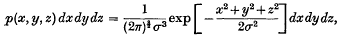
where σ depends on n. Thus r2 (= x2 + y2 + z2) will be approximately distributed as σ2χ2 with three degrees of freedom.