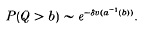During the course of some investigations on the distribution of stress in an elastic solid it was noticed by the senior author that a systematic application of the method of integral transforms to the problem of the indentation of the plane surface of a semi-infinite elastic solid by a rigid punch reduced the problem essentially to one of solving a pair of integral equations belonging to a class which has been studied by Titchmarsh and by Busbridge (4,5). This procedure allows one to obtain the solution for an arbitrary shape of punch by a general method which leads automatically to the solution and avoids the troublesome procedure, adopted by Love (2) in the case of a conical punch, of being obliged to guess appropriate combinations of solutions which will satisfy the prescribed boundary conditions in any special case. Moreover, it can easily be seen that an attempt to apply Love's method to more complicated shapes of punch will lead to considerable analytical difficulties.

In a recent paper Al-Salam(1) has denned a fractional q-integral operator by the basic integral

(1) Where α ≠ 0, −1, −2, …. Using the series definition of the basic integrals, (1·1) is written as

valid for all α

A Hamiltonian structure is presented, which generalizes classical Hamiltonian structure, by assigning a distinct symplectic operator for each unbounded space direction and time, of a Hamiltonian evolution equation on one or more space dimensions. This generalization, called multi-symplectic structures, is shown to be natural for dispersive wave propagation problems. Application of the abstract properties of the multi-symplectic structures framework leads to a new variational principle for space-time periodic states reminiscent of the variational principle for invariant tori, a geometric reformulation of the concepts of action and action flux, a rigorous proof of the instability criterion predicted by the Whitham modulation equations, a new symplectic decomposition of the Noether theory, generalization of the concept of reversibility to space-time and a proof of Lighthill's geometric criterion for instability of periodic waves travelling in one space dimension. The nonlinear Schrödinger equation and the water-wave problem are characterized as Hamiltonian systems on a multi-symplectic structure for example. Further ramifications of the generalized symplectic structure of theoretical and practical interest are also discussed.

This paper is mainly concerned with the distribution of stress near a flat elliptical crack in a body of infinite extent under a uniform tension at infinity perpendicular to the plane of the crack. After an analytical solution of this problem was found the authors received a copy of a paper by Sadowsky and Sternberg (3) in which they solved the more general problem of the stress concentration around a tri-axial ellipsoidal cavity in an elastic body of infinite extent, the body at infinity being in a uniform state of stress whose principal axes are parallel to the axes of the cavity. The method of solution adopted by the present writers for the special case of the elliptical crack is somewhat different from the more general work of Sadowsky and Sternberg, and is, moreover, surprisingly simple, so it seems to be of value to present this solution here.

We consider queueing systems where the workload process is assumed to have an associated large deviation principle with arbitrary scaling: there exist increasing scaling functions (at, vt, t∈R+) and a rate function I such that if (Wt, t∈R+) denotes the workload process, then

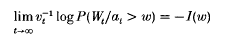
on the continuity set of I. In the case that at = vt = t it has been argued heuristically, and recently proved in a fairly general context (for discrete time models) by Glynn and Whitt[8], that the queue-length distribution (that is, the distribution of supremum of the workload process Q = supt≥0Wt) decays exponentially:

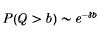
and the decay rate δ is directly related to the rate function I. We establish conditions for a more general result to hold, where the scaling functions are not necessarily linear in t: we find that the queue-length distribution has an exponential tail only if limt→∞at/vt is finite and strictly positive; otherwise, provided our conditions are satisfied, the tail probabilities decay like

As is well illustrated by photographs of their tracks, the majority of β-particles of given initial velocity bave approximately the same range, measured along the path. When the track shows a visible branch, indicating that an exceptionally close encounter has resulted in the ejection of an electron with kinetic energy amounting to an appreciable fraction of that of tbe primary particle, the main track is naturally of less tban tbe average range. A diminution of range may also be expected to follow such of the nuclear deflections as result in the emission of X radiation; this decrease in range indeed affords a possible method of measuring the energy of the radiation emitted in individuai cases and so testing theories such as that of Kramers as to the nature and origin of the continuous X-ray spectrum.

An electron, according to relativity quantum theory, has two different kinds of states of motion, those for which the kinetic energy is positive and those for which it is negative. Only the former, of course, can correspond to actual electrons as observed in the laboratory. The latter, however, must also have a physical meaning, since the theory predicts that transitions will take place from one kind to the other. It has recently been proposed that one should assume that nearly all the possible states of negative energy are occupied, with just one electron in each state in accordance with Pauli's exclusion principle, and that the unoccupied states or ‘holes’ in the negative-energy distribution should be regarded as protons. According to these ideas, when an electron of positive energy makes a transition into one of the unoccupied negative-energy states, we have an electron and proton disappearing simultaneously, their energy being emitted in the form of electromagnetic radiation. The object of the present paper is to calculate the frequency of occurrence of these processes of annihilation of electrons and protons.

The theory of long waves in shallow water under gravity employs two different approaches, which have given rise to a well-known paradox remarked by Stokes, but hitherto not fully resolved. On the one hand it was shown by Airy (1) that, if the pressure at any point in the fluid is equal to the hydrostatic head due to the column of water above it, then no wave form can be propagated without change hi shallow water of uniform depth; on the other hand, it was shown by Rayleigh's theory (8) of the solitary wave that this conclusion may be incorrect. In the present paper an attempt is made to elucidate the paradox. Waves of small amplitude η0 and large horizontal wave-length λ (compared with the depth h of the water) are studied, and it is shown that Airy's conclusion is valid if η0λ2/h3 ia large, whereas the solitary wave has η0λ2/h3 of order unity. Equations of motion are derived corresponding to large, moderate and small values of η0λ2/h3; these can be summarized in a single equation for the profile η(x, t):

due to Boussinesq (3).

It is also shown that the linearized theory of surface waves is valid only if η0/λ and η0λ2/h3 are both small. Some remarks are made on the generation of the solitary wave, and on the breaking of waves on a shelving beach.

In a recent paper we have discussed certain general principles underlying the determination of the most efficient tests of statistical hypotheses, but the method of approach did not involve any detailed consideration of the question of a priori probability. We propose now to consider more fully the bearing of the earlier results on this question and in particular to discuss what statements of value to the statistician in reaching his final judgment can be made from an analysis of observed data, which would not be modified by any change in the probabilities a priori. In dealing with the problem of statistical estimation, R. A. Fisher has shown how, under certain conditions, what may be described as rules of behaviour can be employed which will lead to results independent of these probabilities; in this connection he has discussed the important conception of what he terms fiducial limits. But the testing of statistical hypotheses cannot be treated as a problem in estimation, and it is necessary to discuss afresh in what sense tests can be employed which are independent of a priori probability laws.

It often happens that when two sets of data obtained by observation give slightly different estimates of the true value we wish to know whether the difference is significant. The usual procedure is to say that it is significant if it exceeds a certain rather arbitrary multiple of the standard error; but this is not very satisfactory, and it seems worth while to see whether any precise criterion can be obtained by a thorough application of the theory of probability.

The conditions for equilibrium in an elastically stressed hexagonal aeolotropic medium (transversely isotropic) are formulated, and solutions are found in terms of two ‘harmonic’ functions ø1, ø2, which are solutions of

ν1, ν2 being the roots of a certain quadratic equation.

It is also shown that in the case of axially symmetrical stress systems the solution may be expressed in terms of the third-order differential coefficients of a single stress function Φ.

The solutions for an isotropic medium may be deduced as a special case.

The problems of nuclei of strain in such a hexagonal solid are solved, and the results for zinc and magnesium contrasted with those for an isotropic solid.

Consider bounded sets of points in a Euclidean space Rq of q dimensions. Let h(t) be a continuous increasing function, positive for t>0, and such that h(0) = 0. Then the Hausdroff measure h–mE of a set E in Rq, relative to the function h(t), is defined as follows. Let ε be a small positive number and suppose E is covered by a finite or enumerably infinite sequence of convex sets {Ui} (open or closed) of diameters di less than or equal to ε. Write h–mεE = greatest lower bound for any such sequence {Ui}. Then h–mεE is non-decreasing as ε tends to zero. We define

We show that determining the Jones polynomial of an alternating link is #P-hard. This is a special case of a wide range of results on the general intractability of the evaluation of the Tutte polynomial T(M; x, y) of a matroid M except for a few listed special points and curves of the (x, y)-plane. In particular the problem of evaluating the Tutte polynomial of a graph at a point in the (x, y)-plane is #P-hard except when (x − 1)(y − 1) = 1 or when (x, y) equals (1, 1), (−1, −1), (0, −1), (−1, 0), (i, −i), (−i, i), (j, j2), (j2, j) where j = e2πi/3

In this paper the two-dimensional reflection of surface waves from a vertical barrier in deep water is studied theoretically.

It can be shown that when the normal velocity is prescribed at each point of an infinite vertical plane extending from the surface, the motion on each side of the plane is completely determined, apart from a motion consisting of simple standing waves. In the cases considered here the normal velocity is prescribed on a part of the vertical plane and is taken to be unknown elsewhere. From the condition of continuity of the motion above and below the barrier an integral equation for the normal velocity can be derived, which is of a simple type, in the case of deep water. We begin by considering in detail the reflection from a fixed vertical barrier extending from depth a to some point above the mean surface.

Traced monoidal categories are introduced, a structure theorem is proved for them, and an example is provided where the structure theorem has application.

1. As is well known, the electrical resistance of a metal is very greatly in-creased by the addition of a second metal with which it forms a solid solution. The increase Δρ in the resistivity due to the addition of a small percentage of the second metal is in general independent of the temperature (Matthiessen's rule), though there are oertain exceptions (e.g. Cr in Au). The quaritum-mechanical explanation of both these facts was first given by Nordheim, and may be expressed as follows: the electrical conductivity of any metal may be written in the form

where τ is the “time of relaxation”, equal to half the time between collisions, and N is the effective number of free electrons per unit volume: hence, for the resistivity, we have

Let S be n dimensional Euclidean space and let T be a division of S into cells. Assume that each cell must be either white or black at any time t. At time 0 the cell at the origin, α0, is black and all other cells are white. Let G be some stochastic growth process which tends to change white cells with black neighbours into black cells. Let C(t) be the black shape at time t. For a family, F, of such growth processes we prove the following theorem.

The production of a ‘wake’ behind solid bodies has been treated by different authors. S. Goldstein (1) and S. H. Hollingdale (2) have discussed the laminar wake behind a flat plate, while the wake of a two-dimensional grid has been treated for the turbulent case alone using L. Prandtl's ‘Mischungsweg’ theory by E. Anderlik and Gran Olsson (3), (4).

In this paper we are concerned with a material which can support a finite stress elastically without flow and which flows with constant mobility(1) (or plastic fluidity) when the stresses are sufficiently great. Following Bingham(1) and Houwink(2), such a material is called a Bingham solid and the type of flow (purely) plastic. The transition from elastic to plastic behaviour takes place at the yield point.