The law of large numbers for the empirical density for the pairs of uniformly distributed integers with a given greatest common divisor is a classic result in number theory. We study the large deviations of the empirical density. We will also obtain a rate of convergence to the normal distribution for the central limit theorem. Some generalisations are provided.

A celebrated result of Halász describes the asymptotic behavior of the arithmetic mean of an arbitrary multiplicative function with values on the unit disc. We extend this result to multilinear averages of multiplicative functions providing similar asymptotics, thus verifying a two dimensional variant of a conjecture of Elliott. As a consequence, we get several convergence results for such multilinear expressions, one of which generalises a well known convergence result of Wirsing. The key ingredients are a recent structural result for multiplicative functions with values on the unit disc proved by the authors and the mean value theorem of Halász.

We study transformations of finite modules over Noetherian local rings that attach to a module M a graded module H(x)(M) defined via partial systems of parameters x of M. Despite the generality of the process, which are called j-transforms, in numerous cases they have interesting cohomological properties. We focus on deriving the Hilbert functions of j-transforms and studying the significance of the vanishing of some of its coefficients.

We consider Fell bundles over discrete groups, and the C*-algebra which is universal for representations of the bundle. We define deformations of Fell bundles, which are new Fell bundles with the same underlying Banach bundle but with the multiplication deformed by a two-cocycle on the group. Every graph algebra can be viewed as the C*-algebra of a Fell bundle, and there are many cocycles of interest with which to deform them. We thus obtain many of the twisted graph algebras of Kumjian, Pask and Sims. We demonstate the utility of our approach to these twisted graph algebras by proving that the deformations associated to different cocycles can be assembled as the fibres of a C*-bundle.

Recent workers [1, 3] have proved density theorems about the rational points on K3 surfaces of the form

$$ V:\;X_0^4+cX_1^4=X_2^4+cX_3^4 $$

Let F(z) be a Hecke–Maass form for SL(m, ℤ) with m ⩽ 3, or be the symmetric power lift of a Hecke–Maass form for SL(2, ℤ) if m = 4, 5 and let AF (n, 1, . . ., 1) be the coefficients of L-function attached to F. We establish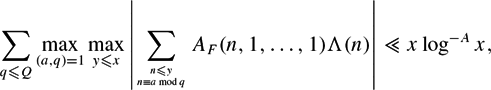

$$\sum_{q\leq Q}\max_{(a,q)=1}\max_{y\leq x}\left|\sum_{n\leq y \atop n\equiv a\bmod q}A_F(n,1, \dots, 1)\Lambda(n)\right| \ll x\log^{-A}x,$$

We show that a positive braid knot has maximal topological 4-genus exactly if it has maximal signature invariant. As an application, we determine all positive braid knots with maximal topological 4-genus and compute the topological 4-genus for all positive braid knots with up to 12 crossings.

In this paper we lift Pestov's Identity on the tangent bundle of a Riemannian manifold M to the bundle of k-tuples of tangent vectors. We also derive an integrated version and a restriction to the frame bundle PkM of k-frames. Finally, we discuss a dynamical application for the parallel transport on $\cal{G}_{or}^{k} (M)$, the Grassmannian of oriented k-planes of M.

In this paper we study the following question: given a semigroup ${\mathcal S}$ of partial isometries acting on a complex separable Hilbert space, when does the selfadjoint semigroup ${\mathcal T}$ generated by ${\mathcal S}$ again consist of partial isometries? It has been shown by Bernik, Marcoux, Popov and Radjavi that the answer is positive if the von Neumann algebra generated by the initial and final projections corresponding to the members of ${\mathcal S}$ is abelian and has finite multiplicity. In this paper we study the remaining case of when this von Neumann algebra has infinite multiplicity and show that, in a sense, the answer in this case is generically negative.

Proposition 2ċ5 of [5] states that a full coaction of a locally compact group on a C*-algebra is nondegenerate if and only if its normalisation is. Unfortunately, the proof there only addresses the forward implication, and we have not been able to find a proof of the opposite implication. This issue is important because the theory of crossed-product duality for coactions requires implicitly that the coactions involved be nondegenerate. Moreover, each type of coaction — full, reduced, normal, maximal, and (most recently) exotic — has its own distinctive properties with respect to duality, making it crucial to be able to convert from one to the other without losing nondegeneracy.

In this paper, we prove a Tb theorem on product spaces $\mathbb{R}$n × $\mathbb{R}$m, where b(x1, x2) = b1(x1)b2(x2), b1 and b2 are para-accretive functions on $\mathbb{R}$n and $\mathbb{R}$m, respectively.

By considering the Bredon analogue of complete cohomology of a group, we show that every group in the class $\cll\clh^{\mathfrak F}{\mathfrak F}$ of type Bredon-FP∞ admits a finite dimensional model for $E_{\frak F}G$.

We also show that abelian-by-infinite cyclic groups admit a 3-dimensional model for the classifying space for the family of virtually nilpotent subgroups. This allows us to prove that for $\mathfrak {F}$, the class of virtually cyclic groups, the class of $\cll\clh^{\mathfrak F}{\mathfrak F}$-groups contains all locally virtually soluble groups and all linear groups over ${\mathbb{C}}$ of integral characteristic.

Assuming CH, the continuum hypothesis, holds we show, by completing an attack first discovered by Roy Davies, that for each α between 0 and 1 there is a subring, in fact a subfield, of R with Hausdorff dimension α.

The category of rational SO(2)–equivariant spectra admits an algebraic model. That is, there is an abelian category ${\mathcal A}$(SO(2)) whose derived category is equivalent to the homotopy category of rational SO(2)–equivariant spectra. An important question is: does this algebraic model capture the smash product of spectra?

The category ${\mathcal A}$(SO(2)) is known as Greenlees' standard model, it is an abelian category that has no projective objects and is constructed from modules over a non–Noetherian ring. As a consequence, the standard techniques for constructing a monoidal model structure cannot be applied. In this paper a monoidal model structure on ${\mathcal A}$(SO(2)) is constructed and the derived tensor product on the homotopy category is shown to be compatible with the smash product of spectra. The method used is related to techniques developed by the author in earlier joint work with Roitzheim. That work constructed a monoidal model structure on Franke's exotic model for the K(p)–local stable homotopy category.

A monoidal Quillen equivalence to a simpler monoidal model category R•-mod that has explicit generating sets is also given. Having monoidal model structures on ${\mathcal A}$(SO(2)) and R•-mod removes a serious obstruction to constructing a series of monoidal Quillen equivalences between the algebraic model and rational SO(2)–equivariant spectra.