In a note (3) published jointly with E. A. Maxwell in 1937, a set of relations was obtained connecting the arithmetic genera Ωi of the i-dimensional characteristic systems of the canonical system on an algebraic Vd. When d is odd these relations are

and when d is even they are

The following ‘partial’ integral equation arises in the quantum theory of fields:

where f(x1x2) = f(x2x1), K(x1x2, y) = K(x2x1, y), and a symmetric solution of the equation is desired. The solution of (1) will be obtained as a special case of the solution of the following equation:

1. The problem considered in this paper arose during an investigation of what Chabauty has called the ‘anomaly’ of convex bodies.

Throughout the paper denotes a closed bounded convex body in three-dimensional Euclidean space , which is symmetric in the origin O and which contains O as an interior point. Such a body determines uniquely a distance-function f(x, y, z) which is defined and finite for each point (x, y, z) of and possesses the following properties

The following work was undertaken in connexion with a device for counting blood cells electronically, which has been developed in the Clinical Pathology Department of the Radcliffe Infirmary with financial assistance from the Medical Research Council and the Nuffield Foundation. Although the results will apply to other types of counter, it will help to fix the ideas if we consider the problem for this specific device. A large number of blood cells, contained in a shallow chamber, are scanned by a photoelectric cell. The depth of the chamber and the concentration of blood cells in solution therein allow blood cells (supposed distributed at random throughout the chamber) to overlap when viewed from above by the scanner. The field of view of the scanner at any instant is somewhat larger than the size of a blood cell, but is, nevertheless, of much the same order of magnitude. With passage of time the chamber moves underneath the photocell so that the field of view traces out a long narrow path not crossing or overlapping itself and only embracing a portion of. the whole chamber. The blood cells have no motion relative to the chamber. As each blood cell comes under the photocell it produces an electrical impulse, whose duration depends upon the size and shape and orientation of the blood cell. These impulses go to a counter, which counts them except that it will not count any impulse which is overlapped by a previous impulse. The problem is to determine the number of blood cells in the chamber from a knowledge of the recorded count and the distribution of the lengths of individual impulses. A further complication arises because it is inadvisable to count two impulses separated only by a very short interval of time, and therefore the counter itself generates some self-paralysing impulses additional to the blood-cell impulses and in a manner which is correlated with them. Until § 3, however, we shall neglect paralysis, because a proper understanding of its effects cannot be reached unless we first know how the system behaves in the absence of paralysis.

This note contains two counter-examples which have a bearing on work published in earlier papers (1, 2, 3) of the sequence. It has been shown that the Parseval formulae for Fourier cosine and sine transforms,

hold in a number of cases when two of the functions concerned are monotonic, and that there are corresponding results for Fourier series. In some of these theorems, the existence of one side of the relevant equation (in the ordinary finite sense) is postulated; others contain no such existence condition, and show that either both sides are finite and equal, or both sides are ‘ + ∞’. In the case of sine transforms, we always obtain theorems of the second type (which is clearly the stronger); but cosine transforms are more troublesome. The first of the examples which we shall give is designed to show that the cosine formula is not always true in the ‘finite or infinite’ sense when two of the functions are monotonic.

1. Let Λ denote any plane lattice of determinant Δ ╪ 0. Then it is well known that the region

contains a pair of generating points of Λ; and that, unless the lattice Λ is of the special form

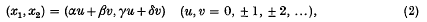
where both α│β, γ│δ are rational, there are an infinity of such pairs in the interior of the region. Minkowski (4) obtained this result by considering the ‘tangent’ parallelogram Пλ,

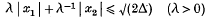
inscribed in the region (1). With simple geometrical arguments, he showed that

(i) Пλ always contains a point of Λ, other than 0,

(ii) if Пλ contains two primitive points of Λ then these generate Λ, except possibly when Λ has points, other than 0, on both coordinate axes.

I write X for the point (x1, x2, …, xn) of n-dimensional Euclidean space Rn. The coordinates x1, x2, …, xn are real numbers. The origin (0, 0,…, 0) is denoted by O. If t is a real number, tX denotes the point (tx1, tx2, …, txn); in particular, − X is the point (−x1, −x2,…, −xn). Also X + Y denotes the point {x1 + y1, x2 + y2, …, xn + yn).

Modifications to the Feynman propagation functions Sp and Dp are suggested in order to deal with field theoretic problems involving the presence in the initial and the final states, of free fermions or bosons, having all values of momentum (and energy) within a certain specified range.

It is shown that for the quantized φ3 field the series expansions for intermediate representation field operators are convergent for summation over all graphs except those containing self-energy and vertex parts. The method used does not permit an investigation of the self-energy and vertex parts.

Let

be n linear forms with real coefficients and determinant Δ = ∥ aij∥ ≠ 0; and denote by M(X) the lower bound of | X1X2 … Xn| over all integer sets (u) ≠ (0). It is well known that γn, the upper bound of M(X)/|Δ| over all sets of forms Xi, is finite, and the value of γn has been determined when n = 2 and n = 3.

In this paper we consider algebraic integers, θ, such that θ and θ¯ (θ ╪ θ¯) are the only algebraic conjugates of θ that lie outside the unit circle.

Let S1 be the set of algebraic integers, ρ, necessarily real, all of whose conjugates, except ρ, satisfy | z < 1.

Experience has shown that the sections of an electronic digital computer which are easiest to maintain are those which have a simple logical structure. Not only can this structure be readily borne in mind by a maintenance engineer when looking for a fault, but it makes it possible to use fault-locating programmes and to test the equipment without the use of elaborate test gear. It is in the control section of electronic computers that the greatest degree of complexity generally arises. This is particularly so if the machine has a comprehensive order code designed to make it simple and fast in operation. In general, for each different order in the code some special equipment must be provided, and the more complicated the function of the order the more complex this equipment. In the past, fear of complicating unduly the control circuits of the machines has prevented the designers of electronic machines from providing such facilities as orders for floating-point operations, although experience with relay machines and with interpretive subroutines has shown how valuable such orders are.

The values of a free-electron eigenfunotion at the carbon nuclei of a conjugated hydrocarbon are found to satisfy a system of algebraic equations. These equations are similar in form to those obtained in the method known as the linear combination of atomic orbitale but only coincide with them for linear polyenes and benzene. The symmetry, degeneracy and energy of the eigenvectors of these free-electron equations correspond exactly to those of the free-electron wave functions found by the usual methods. From this correspondence, a theorem is deduced about the free-electron charge density in alternant hydrocarbons.

In fundamental papers Bernstein (3) and Loève(8) have proved central limit theorems for wide classes of dependent variables. Their theorems are stated in terms of conditional distributions. In the case of dn-dependent variables (see § 3) they assume the existence, as the ‘conditioning’ variates vary, of finite upper bounds for certain conditional absolute moments higher than the second. More recently, Hoeffding and Robbins (7) have proved central limit theorems for m-dependent variables with finite third absolute moments, and Moran(10) has given a direct generalization of the Lindeberg-Lévy theorem for stationary discrete linear scalar processes.

In this paper I find the critical lattices of the region Kt defined by the inequalities | xy | ≤ 1, x2 + y2 ≤ t (t > 0). I deduce in §9 the arithmetic minima of a pair of binary quadratic forms

where f1 is indefinite, f2 is positive definite, and f1, f2 are harmonically related, that is to say

and

Let Em and En be orthogonal Euclidean spaces of dimensions m and n respectively and with the origin of each as their only common point. In a previous paper (3) I gave what was intended to be a proof of the relation

where the dimension of A, dim A, is the Besicovitch dimension, i.e. the number s such that the Hausdorff measure in any dimension greater than s is zero whilst that in any dimension less than s is infinite, where A and B are subsets of En and Em respectively and where A × B is the Cartesian product of A with B.

An exact solution is obtained for the diffraction of a plane harmonic electromagnetic wave incident on a semi-infinite open-ended perfectly conducting circular wave guide.

1. In statistical mechanics, we usually deal with assemblies containing a fixed number of particles in which energy is the only conserved quantity. Recently, Fermi (1) has shown that the angular distribution of the pions produced in high-energy nuclear collisions can be explained if one takes into account the conservation of angular momentum in addition to the conservation of energy. We are, therefore, led to discuss the thermodynamical properties of assemblies characterized by the conservation of two or more parameters. The simplest assumption of this type that we can make is that there are two parameters, say E and P, which are conserved, and that each particle of the assembly can occupy the levels (r, s) (r, s are non-negative integers), where the contribution of the level (r, s) to E is rε0 and to P is sη0. In order to find the entropy, and hence other thermodynamical properties of the system, we have to enumerate the distinct number of ways, p(m, n), in which an assembly of particles corresponding to given values of E = mε0 and P = nη0 can be realized. In this paper we find asymptotic expressions for p(m, n) in the following cases: (a) m is a fixed number, (b) m and n are of the same order. It is assumed here that the number of particles is greater than m and n. We deal with the case (a) in §2 and the case (b) in §4. §3 deals with the asymptotic expansions of the generating function for p(m, n) which are used in §4.

About twenty years ago a number of results were given expressing the sum of n terms of an ordinary hypergeometric series with unit argument in terms of an infinite series of the type 3F2. The interest in the subject was aroused by a theorem due to Ramanujan, who stated that

Let pik (s, t) (i, k = 1, 2, …; s ≤ t) be the transition probabilities of a Markov process in a system with an enumerable set of states. The states are labelled by positive integers, and pik (s, t) is the conditional probability that the system be in state k at time t, given that it was in state i at an earlier time s. If certain regularity conditions are imposed on the pik, they can be shown to satisfy the well-known Kolmogorov equations§