Statement of results. Let g(x) be a given real finite function of a real variable x. Let F(g) denote the class of all real Lebesgue-measurable and finite (though possibly unbounded) functions f(x) which satisfy where η may depend upon f Let F* denote the class of all real f(x) such that exists and satisfies − ∞ ≤l<+∞.

It is shown that the problem of the diffraction of an arbitrary electromagnetic wave by a circular disk can be reduced to the solution of independent scalar problems. These latter problems are of a type which can be reduced to the solution of a Fredholm integral equation of the second kind and are particularly suitable for solution by approximate means at low frequencies.

The propagation of plane waves in a thermo-elastic body placed in a magnetic field has been investigated. It is shown that the problem can be reduced to one of pure thermo-elasticity, provided that the longitudinal elastic wave velocity is suitably increased in the case of infinite electrical conductivity. For finite electrical conductivity and low frequency, however, the thermo-elastic coupling factor is to be increased.

Møller's theory on the concept of energy and its localization in general relativity is applied to calculate the energy of the interior and exterior Schwarzschild fields. It is found that the energy is equal to the (Newtonian) gravitational mass of the material system associated with the fields and that all the energy resides wholly in the material system.

The electromagnetic energy & of the field of a charged particle is calculated, using Møller's theory summarized in the previous paper. The contribution of & to the gravitational mass of the charged particle is discussed, by studying the behaviour of a neutral test particle in its field. The conclusion is that & gives rise to an ‘effective’ gravitational mass of the charged particle, which is equal to the (Newtonian) gravitational mass of the charged particle, plus the mass-equivalence of &. This is contrary to the currently accepted theory, that what we have called the ‘effective’ gravitational mass is equal to the ‘Newtonian’ gravitational mass of the charged particle.

We consider the propagation of thermo-elastic Rayleigh waves in a half space, which has been subjected to large uniform extensions, at constant temperature, in three mutually perpendicular directions, one being perpendicular to the surface, and the extension ratios in the other two directions being equal. Rayleigh waves, assuming (a) isentropic conditions and (b) isothermal conditions, are studied, and the relation of the approximation (a) to the exact thermo-elastic theory is considered.

In a previous paper (l) in this journal L. J. Slater gave expansions of the generalized Whittaker functions . She gave this name to the generalized hypergeometric function in the sense that it is a generalization of the well-known Whittaker function . In this paper series of products of generalized Whittaker functions will be evaluated in terms of such functions or in terms of generalized hypergeometric functions pFp(x). These expansions are These formulae will be proved in § 2 and particular cases will be given in § 3.

The solutions of the equation

obtained by the author in (3) are applied to determine the Kirchhoff-Helmholtz flow past a wedge in which the free stream Mach number has any value from 0 to 1 inclusive. For small wedge angles the results are developed further and expressions are found for the drag coefficient and for the asymptotic shape of the free streamlines far downstream. While general formulae are obtained for an arbitrary functionk(σ) more detailed results are given for the particular function k(σ) which corresponds to the case of a polytropic gas.

It has been shown by Landau(8) that in a uniform plasma with a Maxwelliau velocity distribution longitudinal waves are damped. Penrose(9) has considered more general distributions and developed stability criteria. In particular, if the velocity distribution function has only one maximum, then the plasma is stable. In this paper the values of the Landau damping for some stable single maximum distributions are compared in order to assess the sensitivity of Landau damping to the form of the distribution function, and to investigate the usefulness of approximating to the Landau damping in a Maxwellian plasma by using an algebraically simpler velocity distribution function.

It is shown also that, for at least some velocity distributions having a maximum particle velocity, the behaviour of the plasma can no longer be described in terms of exponential damping, since there will be longer lasting perturbations with phase velocity equal to the maximum particle velocity.

For a gas with a general equation of state the stream function for the flow past a flat plate is determined when the plate is held at an angle ½π–α to the stream. At infinity the Mach number M1 = 1 and free streamlines, on which M1 = 1, extend from the edges of the plate to infinity downstream. The method of solution requires the determination of the correct singularity corresponding to the free stream and the subsequent satisfying of the boundary conditions. The drag coefficient is determined in the form of a contour integral and the computational problems in evaluating the drag are discussed. The integral is evaluated for small values of α for a gas with an equation of state as given by Tomotika and Tamada(6).

In this note we consider the axially symmetric indentation of a transversely isotropic layer resting on a rigid foundation. The corresponding half-space problems both for isotropic and transversely isotropic materials have been solved previously (see (l), (2), (3), p. 455) and, more recently, the present problem has been solved for isotropic materials in (4) and (5) using methods different from that given in this paper. In § 2 the problem is reduced to the solution of a Fredholm integral equation of the second kind. In § 3 and subsequently the case of incomplete penetration by the punch, when the radius of the circle of contact is less than that of the end face of the punch, is considered. Finally, in §4 the results are illustrated by considering a hemispherically ended punch.

The general Tchebysheffian approximation problem is the following: Given a real continuous function g(x) in the interval a ≤ x ≤ b, and a real function f(x; Pj) of prescribed form, continuous in the variable x and the parameters Pj, determine the values of the parameters so that the measure of absolute error or ‘deviation’ of f, shall be as small as possible.

Let {kr} (r = 0, 1, 2, …; 1 ≤ kr ≤ h) be a positively regular, finite Markov chain with transition matrix P = (pjk). For each possible transition j → k let gjk(x)(− ∞ ≤ x ≤ ∞) be a given distribution function. The sequence of random variables {ξr} is defined where ξr has the distribution gjk(x) if the rth transition takes the chain from state j to state k. It is supposed that each distribution gjk(x) admits a two-sided Laplace-Stieltjes transform in a real t-interval surrounding t = 0. Let P(t) denote the matrix {Pjkmjk(t)}. It is shown, using probability arguments, that I − sP(t) admits a Wiener-Hopf type of factorization in two ways for suitable values of s where the plus-factors are non-singular, bounded and have regular elements in a right half of the complex t-plane and the minus-factors have similar properties in an overlapping left half-plane (Theorem 1).

In an earlier paper (Cohen and Coulson(3), referred to hereafter as I), it was shown that satisfactory energy eigenvalues and eigenfunctions for various even σ-states of may be obtained using a single-centre expansion, provided that the radial functions are properly determined. In particular, the ground-state energy at the equilibrium internuclear separation of 2 a.u. was found to be within 0·25% of the exact value (Bates, Ledsham and Stewart (2)), and the eigenfunction reproduced all the characteristics of the exact wave-function. The method has now been extended to the odd σ-states, as well as to the two lowest π-states (2pπu, 3dπg), and the results are in good agreement with the calculations of Bates et al.

Some aspects of generation of water waves by wind and of turbulence in a heterogeneous fluid may be described by the theory of hydrodynamic stability. The technical difficulties of these problems of instability have led to obscurities in the literature, some of which are elucidated in this paper. The stability equation for a basic steady parallel horizontal flow under the influence of gravity is derived carefully, the undisturbed fluid having vertical variations of density and viscosity. Methods of solution of the equation for large Reynolds numbers and for long-wave disturbances are described. These methods are applied to simple models of wind blowing over water and of fresh water flowing over salt water.

Series which behave rather like Taylor's series at more than, one point are described and their convergence is discussed briefly.

Let

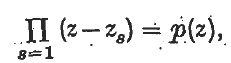
where z, zs are complex numbers and zs are the points, (the base points)about which a function is to be expanded. They need not be distinct. p{z) is a polynomial of degree n. in z. Assume first that z, zs are real and the zs are distinct. Then polynomials pn-1,t(z) may be chosen so that the series

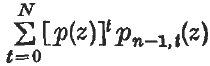
has contact of order N at the points zs with any specified real function which has N derivatives at these points. This is proved merely by rearranging the simplest polynomial in z which has contact of order N with/(z) at z = zs. The term given by t = 0 in (2) allows the series to have the values f(zs) at z = zs; adding the term for t = 1 does not alter the values of the series at z = zs; it allows the series to have a derivative with values f′(zs) at z = z; similarly adding the term for t = 2 does not alter the value of the series or its first derivative at z = zs, it allows the series to have a second derivative with values f″{zs) at z = zs; and so on. If m of the zs coincide then f(z) has mN + m− 1 derivatives there and contact is of order mN + m− 1. If z, zs are complex the result is seen to be valid subject to the obvious generalization of ‘ contact of the ith order’ to complex variables and functions.

The diffraction of a high-frequency plane sound wave by a circular cylinder is investigated when the boundary condition on the cylinder is expressed by means of an equation of the form The special feature of this investigation is that an extended form of the Kirchhoff-Fresnel theory of diffraction is used to find an integral representation for the scattering coefficient. In order to avoid the complicated analysis which would be necessary to evaluate the integrals concerned, the more natural geometrical acoustics approach is used to find the first correction term in the scattering coefficient. Numerical results are given for large and small values of the impedance Z.

This paper is essentially a continuation of the previous one (5) and the notation established therein will be freely repeated. The sequence {ξr} of random variables is defined on a positively regular finite Markov chain {kr} as in (5) and the partial sums and are considered. Let ζn be the first positive ζr and let πjk(y), the ‘ruin’ function or absorption probability, be defined by The main result (Theorem 1) is an asymptotic expression for πjk(y) for large y in the case when , the expectation of ξ1 being computed under the unique stationary distribution for k0, the initial state of the chain, and unconditional on k1.

Using Newtonian theory of gravitation and postulating the existence of informational waves of gravitation, a time-varying gravitational potential is obtained. When a point mass is submitted to such a potential a precession of its orbit, of the right order of magnitude, is obtained. The correct value of the angle of deflexion of light by massive bodies can also be calculated.

An approximate solution of the two-dimensional problem of reflexion of plane harmonic P and S V waves by an irregular boundary is obtained using a modification of Rice's perturbation method of approximation on the assumption that the curvature of the surface is everywhere small. The case of a periodic surface is treated in more detail. It is found that the reflected waves are composed of specularly reflected waves and various diffracted waves, propagating in both horizontal directions if the wavelength of the incident waves is long compared with that of the surface. If the wavelength of incident distortional waves is long compared with that of the surface, the amplitudes of some of the scattered waves decrease exponentially with depth. In general the phases of the waves change on reflexion and the phase angles of the reflected waves are functions of the wavelength of the corrugation and the angle of incidence. It is verified, in the case of zero angle of incidence, that the energy going into the scattered radiation is obtained at the expense of the energy of the specularly reflected waves.