In this paper we determine the complete system of combinantal line-complexes associated with a pencil of quadric surfaces. The method employed is that already used in (I) and (II) to obtain the complete systems of combinantal covariants and contravariants.

The conditions for equilibrium in an elastically stressed hexagonal aeolotropic medium (transversely isotropic) are formulated, and solutions are found in terms of two ‘harmonic’ functions ø1, ø2, which are solutions of

ν1, ν2 being the roots of a certain quadratic equation.

It is also shown that in the case of axially symmetrical stress systems the solution may be expressed in terms of the third-order differential coefficients of a single stress function Φ.

The solutions for an isotropic medium may be deduced as a special case.

The problems of nuclei of strain in such a hexagonal solid are solved, and the results for zinc and magnesium contrasted with those for an isotropic solid.

In my book The Theory and Applications of Harmonic Integrals (hereinafter referred to as H. I.), Chapter iv is devoted to the application of the theory to algebraic varieties. In order to introduce harmonic integrals on an algebraic variety I have to assign a metric to the variety; this metric is not related to the variety in any invariant sense, and indeed its introduction is extremely artificial. Nevertheless it turns out that we can deduce from the properties of the harmonic integrals a number of properties of the variety which are birationally invariant, that is, do not depend on the choice of metric. This remarkable fact seems to indicate either that the invariant properties in question should be obtainable directly without the introduction of the harmonic integrals, or that the metric introduced is not so artificial as it first appeared to be. This note is intended to examine this question.

It has been noticed by various authors that the use of the hodograph transformation for problems of compressible fluid flow leads to flows having singularities where the acceleration becomes infinite, streamlines have cusps and the solution of the equations of motion in the hodograph plane ceases to represent any possible physical flow. In this paper we investigate the nature of the singularities which can occur in the representation of one plane upon another and apply our results to the hodograph transformation. Finally, we discuss the significance for practical purposes of such singularities and in particular their connexion with the occurrence of shock waves.

Recent studies by Debye (1), Bloch (2), Stoner (3) and Guggenheim (4) expressing somewhat divergent views suggest that there is still some confusion and uncertainty in the method of application of the thermodynamic argument to magnetic phenomena. The first effective contribution to the subject was made by Larmor (5) over fifty years ago, and developing this further he finally proposed in 1929 a sufficient basis for a general theory of the whole range of phenomena. At about the same time (1927), and apparently in ignorance of Larmor's earlier work, Debye(1) also gave a brief outline of the thermodynamic aspects of the subject, starting, however, from much more tentative magnetic ideas and formulae which are now known to be without adequate physical justification. In 1933, Bloch (2) elaborated the argument still further, using, however, basic ideas more akin to those employed by Larmor, but derived by a very specialized argument. Then in 1935, using the same fundamental equation as Debye, Stoner revived the discussion with a systematic survey of the theoretical results bearing on the thermodynamic aspects of the subject, attempting later (6) to justify the basic magnetic ideas by a discussion which he now admits is not entirely satisfactory.

It is apparent from the two previous papers of the same main title (1, 2) that velocity distributions in steady rectilinear plastic flow of a Bingham solid between moving boundaries are not easy to determine, even when the boundaries are of simple shape. In the familiar case of a Newtonian liquid (which can be regarded as a special case of a Bingham solid with zero yield value) the velocity ω is a harmonic function and can be obtained by a conformal transformation of the region of flow of the type

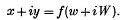
In order to generalize and include materials of finite yield value, in which ω is not harmonic, one must first regard the Newtonian case from a slightly different point of view. The transformation

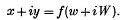
must be regarded as defining a change of coordinates, from Cartesian coordinates x, y to the natural curvilinear coordinates for a particular problem ω, W, one of which is the velocity. For a Bingham solid in general, it is shown in the present paper that natural coordinates ω, W exist, but are not obtainable by a conformal transformation from Cartesian coordinates, except in the limit when the yield value tends to zero. In practice it may be difficult to determine the natural coordinate system in a given problem, but when it is found the velocity distribution is automatically known.

1. In this paper we find explicitly the base for the prime ideal associated with any irreducible Vd−1 on a Segre variety, or a Veronesean variety, Vd. This work extends that of an earlier paper (1) in which the base was found when the Vd−1 is a complete intersection of Vd with one primal. As particular examples we can write down the base for any irreducible curve on a quadric surface, a Veronese surface or a Del Pezzo surface. We also show how the base for any prime ideal changes under a Veronesean transformation.

The problem of the propagation of steady disturbance in a semi-infinite supersonic stream moving parallel to and bounded on one side by a subsonic stream is discussed and the complete solution obtained for any assumed form of incident disturbance. It is shown that a local initial disturbance generally produces a reflected wave extending to infinity both upstream and downstream of the initial disturbance. A (positive) pressure pulse as an incident wave produces pressure upstream and rarefaction downstream and the magnitude of the effects is calculated in a particular case. Conditions along the axis of symmetry are calculated for the subsonic region in this case.

1. The general problem. In the first three papers under the same main title (1, 2, 3), attention has been confined almost entirely to a discussion of steady flow. The equations to be solved in order to determine velocity distributions in non-steady rectilinear plastic flow were given in § 1 of the third paper (3). On the assumptions of isotropy and incompressibility, the conditions of the general problem are as follows.

Heisenberg and Pauli (1) have shown how to quantize field theories derived from a Lagrangian containing first derivatives of the field quantities only. The present paper extends the theory of quantization of fields to the case of higher order Lagrangians, i.e. Lagrangians in which higher derivatives than the first appear. It is shown how such field equations can be put into Hamiltonian form and how the quantization can subsequently be carried out. Both the cases of Einstein-Bose and Fermi-Dirac quantization are discussed. It is established that the quantization is relativistically invariant and consistent with the field equations. An interesting feature of the present theory is that the Hamiltonian proves to be different, in general, from the integral of the 4–4 component of the energy momentum tensor.

It is known as a result of various experiments on slow neutrons (1) that a heavy nucleus possesses an enormous number of energy levels which are very closely spaced if the nucleus is highly excited. Strong theoretical reasons for the existence of this great number of levels were given by Bohr (2) and since then various attempts have been made to calculate the number of energy levels of a heavy nucleus. In the first of these, due to Bethe(3), it was assumed that the interaction between the nucleons was small so that the nucleus could be treated as a gas. The alternative assumption, that we may consider the interaction to be large in comparison with the kinetic energy of the nucleons, was proposed by Bohr and Kalckar(4). In the present note we assume as our model a nucleus consisting of neutrons and protons independent of one another; we then have a neutron-gas in equilibrium with a proton-gas, Fermi-Dirac statistics being applied to both.

If the probability differential of a set of stochastic variates contains k unknown parameters, the statistical hypotheses concerning them may be simple or composite. The hypothesis leading to a complete specification of the values of the k parameters is called a simple hypothesis, and the one leading to a collection of admissible sets a composite hypothesis. In this paper we shall be concerned with the testing of these two types of hypotheses on the basis of a large number of observations from any probability distribution satisfying some mild restrictions and their use in problems of estimation.

The secondary emission electron multiplier is chosen to illustrate the phenomenon of ‘cascade multiplication’. A method is given for deriving the semi-invariants of the probability distribution for the number of output electrons after any number of identical stages of multiplication, in terms of the corresponding semi-invariants for a single stage. The output distribution is not, in general, either of the Poisson or Gaussian types, though it tends to a limiting shape as the number of stages becomes very large. The special case in which each stage replaces a single primary electron by a Poisson distribution of secondaries is considered. The overall output distribution after many stages is still not Gaussian unless the mean amplification per stage is large compared with unity.

Some new measurements of isotropic turbulence produced behind a biplane grid have been made at high Reynolds numbers, and these results are compared with the predictions of the theory of local isotropy developed by A. N. Kolmogoroff. The transverse double-velocity correlation has been measured at mesh Reynolds numbers up to 3·2 × 105, and the observed form agrees well with the predicted form. Measurements of the skewness factor of velocity differences over finite intervals have also been made, and the factor is nearly constant and equal to −0·38, if the interval is small compared with the integral scale. The invariance of dimensionless functions of the velocity derivatives has been confirmed for the flattening factor of ∂u/∂x, namely,

which is nearly constant over a wide range of conditions. It is concluded that the theory of local isotropy is substantially correct for isotropic turbulence of high Reynolds number.

Several authors (1, 2, 3) have discussed the formulation of quantum electrodynamics in the configuration space of the light quanta; they conclude that no meaning can be given to the position of a light quantum, but it is not made clear whether this situation is due to the vanishing of the charge or of the rest mass. However, since the previous discussion (2, 3), various neutral particles of non-vanishing rest mass have been postulated, and it is of interest to consider what meaning can be given to the position of such particles. We shall at first consider integral spin and Bose statistics; the case of spin ½ and Fermi statistics is simpler and is briefly discussed in the last section.

The production of a ‘wake’ behind solid bodies has been treated by different authors. S. Goldstein (1) and S. H. Hollingdale (2) have discussed the laminar wake behind a flat plate, while the wake of a two-dimensional grid has been treated for the turbulent case alone using L. Prandtl's ‘Mischungsweg’ theory by E. Anderlik and Gran Olsson (3), (4).

In the following I discuss the properties, in particular the completeness of the set of eigenfunctions, of an eigenvalue problem which differs from the well-known Sturm-Liouville problem by the boundary condition being of a rather unusual type.

The problem arises in the theory of nuclear collisions, and for our present purpose we take it in the simplified form

where 0 ≤ x ≤ 1. V(x) is a given real function, which we assume to be integrable and to remain between the bounds ± M, and W is an eigenvalue. The eigenfunction ψ(x) is subject to the boundary conditions

and

When impact occurs between clean metal surfaces, plastic flow of the metal usually takes place at the points of real contact, so that the pressures developed are as high as the dynamic yield pressure of the metal concerned. Early experiment show that if the surfaces are covered with a thin film of a highly viscous liquid, the pressures developed and transmitted through the liquid film may be sufficiently great to produce plastic deformation of the metal, even though no metallic contact occurs through the film (1). The existence of these high pressures in the liquid layer means that extremely high rates of flow and shear may be developed in the liquid film, and that the energy dissipated in overcoming viscous flow may lead to an appreciable temperature rise in the liquid. Even in much gentler impacts, where plastic deformation of the metal surfaces does not occur, very high pressures, rates of flow and shear, etc., may be developed in the liquid film. These effects are of great interest in any study of collisions through liquids; they are of particular significance in the study of the mechanism of detonation of liquid explosives by impact.

A method is presented for the accurate numerical treatment of molecular vibration problems in which the potential energy function is of the form

The treatment is carried through in detail for the case V(q) = Aq2 + Bq4, which, in most instances affords an adequate description of the potential. There is no restriction on the relative magnitudes of quadratic and quartic terms so that the method is equally applicable to the purely anharmonic oscillations occurring in types of ring bending (1), where V(q) = aq4.

An approximate formula is derived for the energy levels in the general case. The case V = aq4 affords an illustration of the accurate treatment; the first five eigen-values and eigen-functions are computed and from them the associated transitionprobabilities. Numerical results are presented in a form convenient for further application. On comparison the approximate formula is found to yield results in error by approximately 1 %, the error decreasing for the higher levels for which the formula tends to a B.W.K. expression. In conclusion a ground-state eigen-function of simple analytical form is found to approximate remarkably well to the case of purely quartic vibrations.

In three papers (1, 2, 3) Bhabha has set up a new theory for relativistic particles of any spin, and has suggested that a particular wave equation of half-odd spin, classified as (, ½), may be applicable to the proton. It is therefore of interest to study this equation and to calculate results which could perhaps be compared with experiment; since in the non-relativistic limit the particle obeys Dirac's equation, it is sufficient to consider the behaviour at energies large compared to the rest mass. Here the important problem is the calculation of scattering cross-sections for cosmic-ray processes.