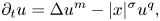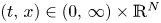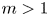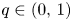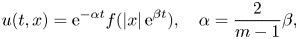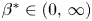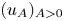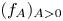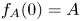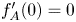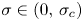1. Introduction and main results
The goal of the present paper (and also of its second part [Reference Iagar, Laurençot and Sánchez22]) is to address the problem of existence and classification of some specific solutions to the following porous medium equation with strong absorption
in the range of exponents
On the one hand, equation (1.1) features, in the range of exponents given in (1.2), a competition between the degenerate diffusion term, which tends to conserve the total mass of the solutions while expanding their supports, and the absorption term which leads to a loss of mass. As it has been established and will be explained below, absorption becomes stronger as its exponent $q$![]() decreases and dominant in the range we are dealing with, leading to specific, although sometimes surprising phenomena such as finite time extinction, instantaneous shrinking and localization of the supports of the solutions. On the other hand, the weight $|x|^{\sigma }$
decreases and dominant in the range we are dealing with, leading to specific, although sometimes surprising phenomena such as finite time extinction, instantaneous shrinking and localization of the supports of the solutions. On the other hand, the weight $|x|^{\sigma }$![]() with $\sigma >0$
with $\sigma >0$![]() affects the absorption in the sense of enhancing its effect over regions far away from the origin, where $|x|$
affects the absorption in the sense of enhancing its effect over regions far away from the origin, where $|x|$![]() is large, while reducing its strength near $x=0$
is large, while reducing its strength near $x=0$![]() , where $|x|^{\sigma }$
, where $|x|^{\sigma }$![]() is almost zero (and formally there is even no absorption at $x=0$
is almost zero (and formally there is even no absorption at $x=0$![]() ).
).
The balance between these two effects has been best understood in the spatially homogeneous case $\sigma =0$![]() of equation (1.1). A lot of development has been done several decades ago in the range $q>m>1$
of equation (1.1). A lot of development has been done several decades ago in the range $q>m>1$![]() where the diffusion is strong and the absorption is not leading the dynamics of the equations, see for example [Reference Kamin and Peletier27–Reference Leoni32, Reference Peletier and Terman34] and references therein. In this range, the previous knowledge of the porous medium equation and its self-similar behaviour had a strong influence in developing the theory. The intermediate range $1< q\leq m$
where the diffusion is strong and the absorption is not leading the dynamics of the equations, see for example [Reference Kamin and Peletier27–Reference Leoni32, Reference Peletier and Terman34] and references therein. In this range, the previous knowledge of the porous medium equation and its self-similar behaviour had a strong influence in developing the theory. The intermediate range $1< q\leq m$![]() is not yet totally understood in higher space dimensions. In dimension $N=1$
is not yet totally understood in higher space dimensions. In dimension $N=1$![]() it has been shown that solutions are global in time but their supports are localized if the initial condition is compactly supported; that is, there exists a radius $R>0$
it has been shown that solutions are global in time but their supports are localized if the initial condition is compactly supported; that is, there exists a radius $R>0$![]() not depending on time such that ${\rm supp}\,u(t)\subseteq B(0,\,R)$
not depending on time such that ${\rm supp}\,u(t)\subseteq B(0,\,R)$![]() for any $t>0$
for any $t>0$![]() . Self-similar solutions might become unbounded [Reference Chaves, Vázquez and Walias12, Reference McLeod, Peletier and Vázquez33] and thus a delicate analysis of the large time behaviour, involving the formation of boundary layers, is needed, see [Reference Chaves and Vázquez11]. Such descriptions are still lacking in dimension $N\geq 2$
. Self-similar solutions might become unbounded [Reference Chaves, Vázquez and Walias12, Reference McLeod, Peletier and Vázquez33] and thus a delicate analysis of the large time behaviour, involving the formation of boundary layers, is needed, see [Reference Chaves and Vázquez11]. Such descriptions are still lacking in dimension $N\geq 2$![]() .
.
More related to our study, still assuming that $\sigma =0$![]() , the range $q\in (0,\,1)$
, the range $q\in (0,\,1)$![]() is the most striking one, where the absorption term dominates the diffusion and leads to two new mathematical phenomena. On the one hand, the finite time extinction stemming from the ordinary differential equation $\partial _t u=-u^q$
is the most striking one, where the absorption term dominates the diffusion and leads to two new mathematical phenomena. On the one hand, the finite time extinction stemming from the ordinary differential equation $\partial _t u=-u^q$![]() obtained by neglecting the diffusion has been established by Kalashnikov [Reference Kalasnikov25, Reference Kalashnikov26], emphasizing the dominance of the absorption term. On the other hand, instantaneous shrinking of supports of solutions to equation (1.1) (with $\sigma =0$
obtained by neglecting the diffusion has been established by Kalashnikov [Reference Kalasnikov25, Reference Kalashnikov26], emphasizing the dominance of the absorption term. On the other hand, instantaneous shrinking of supports of solutions to equation (1.1) (with $\sigma =0$![]() ) emanating from a bounded initial condition $u_0$
) emanating from a bounded initial condition $u_0$![]() such that $u_0(x)\to 0$
such that $u_0(x)\to 0$![]() as $|x|\to \infty$
as $|x|\to \infty$![]() takes place; that is, for any non-negative initial condition $u_0\in L^{\infty }(\mathbb {R}^N)$
takes place; that is, for any non-negative initial condition $u_0\in L^{\infty }(\mathbb {R}^N)$![]() such that $u_0(x)\to 0$
such that $u_0(x)\to 0$![]() as $|x|\to \infty$
as $|x|\to \infty$![]() and $\tau >0$
and $\tau >0$![]() , there is $R(\tau )>0$
, there is $R(\tau )>0$![]() such that ${\rm supp}\,u(t)\subseteq B(0,\,R(\tau ))$
such that ${\rm supp}\,u(t)\subseteq B(0,\,R(\tau ))$![]() for all $t\ge \tau$
for all $t\ge \tau$![]() . This rather unexpected behaviour is once more due to the strength of the absorption, which involves a very quick loss of mass and has been proved in [Reference Abdullaev1] after borrowing ideas from previous works [Reference Evans and Knerr14, Reference Kalashnikov26] devoted to the semilinear case. Finer properties of the dynamics of equation (1.1) for $\sigma =0$
. This rather unexpected behaviour is once more due to the strength of the absorption, which involves a very quick loss of mass and has been proved in [Reference Abdullaev1] after borrowing ideas from previous works [Reference Evans and Knerr14, Reference Kalashnikov26] devoted to the semilinear case. Finer properties of the dynamics of equation (1.1) for $\sigma =0$![]() in this range, such as the behaviour near the extinction time or even the extinction rates, are still lacking in a number of cases and seem (up to our knowledge) to be available only when $m+q=2$
in this range, such as the behaviour near the extinction time or even the extinction rates, are still lacking in a number of cases and seem (up to our knowledge) to be available only when $m+q=2$![]() in [Reference Galaktionov and Vázquez16], revealing a case of asymptotic simplification. Completing this picture with the cases when $m+q\neq 2$
in [Reference Galaktionov and Vázquez16], revealing a case of asymptotic simplification. Completing this picture with the cases when $m+q\neq 2$![]() appears to be a rather complicated open problem.
appears to be a rather complicated open problem.
Drawing our attention now to the spatially inhomogeneous equation (1.1) when $\sigma >0$![]() , recent results have shown that the magnitude of $\sigma$
, recent results have shown that the magnitude of $\sigma$![]() has a very strong influence on the dynamics of equation (1.1) and, in some cases, the weight actually allows for a better understanding of the dynamics. More precisely, the analysis performed by Belaud and coworkers [Reference Belaud3–Reference Belaud and Shishkov5], along with the instantaneous shrinking of supports for bounded solutions to equation (1.1) proved in [Reference Iagar, Laurençot and Sánchez21], shows that, for $0<\sigma <\sigma _c$
has a very strong influence on the dynamics of equation (1.1) and, in some cases, the weight actually allows for a better understanding of the dynamics. More precisely, the analysis performed by Belaud and coworkers [Reference Belaud3–Reference Belaud and Shishkov5], along with the instantaneous shrinking of supports for bounded solutions to equation (1.1) proved in [Reference Iagar, Laurençot and Sánchez21], shows that, for $0<\sigma <\sigma _c$![]() , any non-negative solution to equation (1.1) with bounded initial condition vanishes in finite time. A more direct proof of this result is given by the authors in the recent short note [Reference Iagar and Laurençot20]. On the contrary, after developing the general theory of well-posedness for equation (1.1), we have focussed on the range $\sigma >\sigma _c$
, any non-negative solution to equation (1.1) with bounded initial condition vanishes in finite time. A more direct proof of this result is given by the authors in the recent short note [Reference Iagar and Laurençot20]. On the contrary, after developing the general theory of well-posedness for equation (1.1), we have focussed on the range $\sigma >\sigma _c$![]() in our previous work [Reference Iagar, Laurençot and Sánchez21] and proved that, in the latter, finite time extinction depends strongly on how concentrated is the initial condition in a neighbourhood of the origin. More precisely, initial data which are positive in a ball $B(0,\,\delta )$
in our previous work [Reference Iagar, Laurençot and Sánchez21] and proved that, in the latter, finite time extinction depends strongly on how concentrated is the initial condition in a neighbourhood of the origin. More precisely, initial data which are positive in a ball $B(0,\,\delta )$![]() give rise to solutions with a non-empty positivity set for all times,
give rise to solutions with a non-empty positivity set for all times,
when $\sigma >\sigma _c$![]() , while initial data which vanish in a suitable way as $x\to 0$
, while initial data which vanish in a suitable way as $x\to 0$![]() and with a sufficiently small $L^{\infty }$
and with a sufficiently small $L^{\infty }$![]() norm lead to solutions vanishing in finite time, as proved in [Reference Iagar and Laurençot20] where optimal conditions are given. All these cases of different dynamics are consequences of the two types of competitions explained in the previous paragraphs.
norm lead to solutions vanishing in finite time, as proved in [Reference Iagar and Laurençot20] where optimal conditions are given. All these cases of different dynamics are consequences of the two types of competitions explained in the previous paragraphs.
The exponent $\sigma _c=2(1-q)/(m-1)$![]() thus appears to separate the onset of extinction in finite time for arbitrary non-negative and bounded initial conditions which occurs for lower values of $\sigma$
thus appears to separate the onset of extinction in finite time for arbitrary non-negative and bounded initial conditions which occurs for lower values of $\sigma$![]() and the positivity property (1.3) which is known to take place for higher values of $\sigma$
and the positivity property (1.3) which is known to take place for higher values of $\sigma$![]() , in particular for initial conditions which are positive in a ball $B(0,\,\delta )$
, in particular for initial conditions which are positive in a ball $B(0,\,\delta )$![]() . According to [Reference Iagar and Laurençot20], when $\sigma =\sigma _c$
. According to [Reference Iagar and Laurençot20], when $\sigma =\sigma _c$![]() , there are non-negative solutions to equation (1.1) vanishing in finite time, their initial conditions having a sufficiently small $L^\infty$
, there are non-negative solutions to equation (1.1) vanishing in finite time, their initial conditions having a sufficiently small $L^\infty$![]() -norm and decaying to zero in a suitable way as $x\to 0$
-norm and decaying to zero in a suitable way as $x\to 0$![]() , and the issue we address here is whether the positivity property (1.3) also holds true for some solutions to equation (1.1) when $\sigma =\sigma _c$
, and the issue we address here is whether the positivity property (1.3) also holds true for some solutions to equation (1.1) when $\sigma =\sigma _c$![]() . We actually construct specific solutions to equation (1.1) with $\sigma =\sigma _c$
. We actually construct specific solutions to equation (1.1) with $\sigma =\sigma _c$![]() featuring this property and these solutions turn out to have an exponential self-similar form as explained in detail below. In particular, they are defined for all $t\in \mathbb {R}$
featuring this property and these solutions turn out to have an exponential self-similar form as explained in detail below. In particular, they are defined for all $t\in \mathbb {R}$![]() .
.
Main results. We are looking in this paper for some special solutions to equation (1.1) with $m$![]() , $q$
, $q$![]() and $\sigma =\sigma _c$
and $\sigma =\sigma _c$![]() as in (1.2) having an exponential self-similar form; that is,
as in (1.2) having an exponential self-similar form; that is,
Notice that solutions as in (1.4) are actually defined for all $t\in (-\infty,\,\infty )$![]() ; that is, they are not only global in time but eternal. Even if solutions of form (1.4) are rather unexpected for parabolic equations due to the irreversibility of time, several equations are known to have such solutions but usually in critical cases separating different behaviours. Parabolic equations featuring this property include the two-dimensional Ricci flow [Reference Daskalopoulos and Sesum13, Reference Hamilton18], the fast diffusion equation with critical exponent $m_c=(N-2)/N$
; that is, they are not only global in time but eternal. Even if solutions of form (1.4) are rather unexpected for parabolic equations due to the irreversibility of time, several equations are known to have such solutions but usually in critical cases separating different behaviours. Parabolic equations featuring this property include the two-dimensional Ricci flow [Reference Daskalopoulos and Sesum13, Reference Hamilton18], the fast diffusion equation with critical exponent $m_c=(N-2)/N$![]() in space dimension $N\geq 3$
in space dimension $N\geq 3$![]() [Reference Galaktionov, Peletier and Vázquez15], a viscous Hamilton–Jacobi equation featuring singular diffusion of $p$
[Reference Galaktionov, Peletier and Vázquez15], a viscous Hamilton–Jacobi equation featuring singular diffusion of $p$![]() -Laplacian type, $p\in (2N/(N+1),\,2)$
-Laplacian type, $p\in (2N/(N+1),\,2)$![]() and critical gradient absorption [Reference Iagar and Laurençot19], and the related reaction-diffusion equation $\partial _t u - \Delta u^m - |x|^\sigma u^q=0$
and critical gradient absorption [Reference Iagar and Laurençot19], and the related reaction-diffusion equation $\partial _t u - \Delta u^m - |x|^\sigma u^q=0$![]() [Reference Iagar and Sánchez23, Reference Iagar and Sánchez24]. Concerning the latter, the critical value of $\sigma$
[Reference Iagar and Sánchez23, Reference Iagar and Sánchez24]. Concerning the latter, the critical value of $\sigma$![]() is exactly the same as in (1.2), but the dynamic properties of the solutions strongly differ from the present work, since the spatially inhomogeneous part is a source term, introducing mass to the equation. Eternal solutions are also available for kinetic equations, such as the spatially homogeneous Boltzmann equation for Maxwell molecules [Reference Bobylev and Cercignani7, Reference Cabannes9] or Smoluchowski's coagulation equation with coagulation kernel of homogeneity one [Reference Bertoin6, Reference Bonacini, Niethammer and Velázquez8]. Let us finally mention that, besides solutions of the form (1.4), another important class of self-similar eternal solutions of evolution problems is that of travelling wave solutions of form $(t,\,x)\mapsto u(x-ct)$
is exactly the same as in (1.2), but the dynamic properties of the solutions strongly differ from the present work, since the spatially inhomogeneous part is a source term, introducing mass to the equation. Eternal solutions are also available for kinetic equations, such as the spatially homogeneous Boltzmann equation for Maxwell molecules [Reference Bobylev and Cercignani7, Reference Cabannes9] or Smoluchowski's coagulation equation with coagulation kernel of homogeneity one [Reference Bertoin6, Reference Bonacini, Niethammer and Velázquez8]. Let us finally mention that, besides solutions of the form (1.4), another important class of self-similar eternal solutions of evolution problems is that of travelling wave solutions of form $(t,\,x)\mapsto u(x-ct)$![]() in space dimension $N=1$
in space dimension $N=1$![]() , which are available for scalar conservation laws and parabolic equations such as the celebrated Fisher-KPP equation, see [Reference Cantrell and Cosner10, Reference Gilding and Kersner17, Reference Serre35] and the references therein.
, which are available for scalar conservation laws and parabolic equations such as the celebrated Fisher-KPP equation, see [Reference Cantrell and Cosner10, Reference Gilding and Kersner17, Reference Serre35] and the references therein.
Returning to ansatz (1.4), setting $\xi =|x|{\rm e}^{\beta t}$![]() and performing some direct calculations, we readily find that the self-similar exponents must satisfy the condition
and performing some direct calculations, we readily find that the self-similar exponents must satisfy the condition
where $\beta$![]() becomes a free parameter for our analysis, while the profile $f$
becomes a free parameter for our analysis, while the profile $f$![]() solves the differential equation
solves the differential equation
The solutions to equation (1.6) we are looking for in this first part of a two-part work are solutions taking positive values at $\xi =0$![]() . To this end, let us observe that we can fix, without loss of generality, the initial condition as
. To this end, let us observe that we can fix, without loss of generality, the initial condition as
Indeed, given $a>0$![]() and a solution $f$
and a solution $f$![]() to (1.6)–(1.7), we can readily obtain by direct calculations that the rescaled function
to (1.6)–(1.7), we can readily obtain by direct calculations that the rescaled function
solves (1.6) with initial conditions $g(0;a)=a$![]() , $g'(0;a)=0$
, $g'(0;a)=0$![]() . This leaves us with the task of solving the Cauchy problem (1.6)–(1.7), which is performed in the next result.
. This leaves us with the task of solving the Cauchy problem (1.6)–(1.7), which is performed in the next result.
Theorem 1.1 Let $m$![]() , $q$
, $q$![]() and $\sigma =\sigma _c$
and $\sigma =\sigma _c$![]() as in (1.2). There exists a unique exponent $\beta ^*>0$
as in (1.2). There exists a unique exponent $\beta ^*>0$![]() $($
$($![]() and corresponding $\alpha ^*=2\beta ^*/(m-1))$
and corresponding $\alpha ^*=2\beta ^*/(m-1))$![]() such that, for $\alpha =\alpha ^*$
such that, for $\alpha =\alpha ^*$![]() and $\beta =\beta ^*$
and $\beta =\beta ^*$![]() , the Cauchy problem (1.6)–(1.7) has a compactly supported, non-negative and non-increasing solution $f^*\in C^1([0,\,\infty ))$
, the Cauchy problem (1.6)–(1.7) has a compactly supported, non-negative and non-increasing solution $f^*\in C^1([0,\,\infty ))$![]() with $(f^*)^m\in C^2([0,\,\infty ))$
with $(f^*)^m\in C^2([0,\,\infty ))$![]() . The function $U^*$
. The function $U^*$![]() defined by
defined by
is then a self-similar solution to equation (1.1) in exponential form (1.4).
Let us point out that, in strong contrast with the range $\sigma >2(1-q)/(m-1)$![]() analysed in [Reference Iagar, Laurençot and Sánchez21] and where the self-similarity exponents were uniquely determined, in the present case we have two free parameters for the shooting technique: both the initial value of the solution at $x=0$
analysed in [Reference Iagar, Laurençot and Sánchez21] and where the self-similarity exponents were uniquely determined, in the present case we have two free parameters for the shooting technique: both the initial value of the solution at $x=0$![]() and the self-similar exponent $\beta$
and the self-similar exponent $\beta$![]() . Thus, in order to have uniqueness, we need to fix this initial value in view of rescaling (1.8), as explained above.
. Thus, in order to have uniqueness, we need to fix this initial value in view of rescaling (1.8), as explained above.
One of the interesting features of this work is the fact that the proof of theorem 1.1 is based on a mix between various techniques. We employ mainly a shooting technique with respect to the free parameter $\beta$![]() , but in order to study the interface behaviour and establish the uniqueness in theorem 1.1, we transform (1.6) into a quadratic three-dimensional autonomous dynamical system and study a specific local behaviour and critical point in the associated phase space. Let us stress here that we have to go deeper than the analogous study of the interface behaviour in [Reference Iagar, Laurençot and Sánchez21, § 4], since in some cases we need a second order local expansion near the interface point.
, but in order to study the interface behaviour and establish the uniqueness in theorem 1.1, we transform (1.6) into a quadratic three-dimensional autonomous dynamical system and study a specific local behaviour and critical point in the associated phase space. Let us stress here that we have to go deeper than the analogous study of the interface behaviour in [Reference Iagar, Laurençot and Sánchez21, § 4], since in some cases we need a second order local expansion near the interface point.
We end up this presentation by mentioning that the present work is the first part of a two-part analysis of eternal solutions to equation (1.1) and will be followed by a companion work [Reference Iagar, Laurençot and Sánchez22] in which a second and rather surprising type of profiles, presenting a dead-core, is identified and classified, by employing a quite different bunch of techniques based on the complete analysis of an auxiliary dynamical system. Altogether, the existence of such a variety of self-similar solutions in exponential form shows that the dynamics of equation (1.1) in the critical case $\sigma =\sigma _c$![]() is expected to be rather complex and to depend on many features of the initial conditions (such as concentration near $x=0$
is expected to be rather complex and to depend on many features of the initial conditions (such as concentration near $x=0$![]() , magnitude of $\|u_0\|_{\infty }$
, magnitude of $\|u_0\|_{\infty }$![]() and location of the points where the maximum is attained, to name but a few) and is definitely a challenging problem.
and location of the points where the maximum is attained, to name but a few) and is definitely a challenging problem.
2. Proof of theorem 1.1
The proof of theorem 1.1 is based on a shooting method with respect to the free exponent $\beta$![]() and follows the same strategy as [Reference Iagar, Laurençot and Sánchez21, § 4]. However, a number of preparatory results are proved in a different way and the analysis near the interface requires to be improved in some cases with the help of a phase space analysis. We divide this section into several subsections containing the main steps of the proof.
and follows the same strategy as [Reference Iagar, Laurençot and Sánchez21, § 4]. However, a number of preparatory results are proved in a different way and the analysis near the interface requires to be improved in some cases with the help of a phase space analysis. We divide this section into several subsections containing the main steps of the proof.
2.1 Existence of a compactly supported self-similar solution
Let $\beta >0$![]() and $\alpha = 2\beta /(m-1)$
and $\alpha = 2\beta /(m-1)$![]() . Recalling the differential equation (1.6) satisfied by the self-similar profiles $f$
. Recalling the differential equation (1.6) satisfied by the self-similar profiles $f$![]() and setting for simplicity $F=f^m$
and setting for simplicity $F=f^m$![]() , we study, as explained in the Introduction, the Cauchy problem
, we study, as explained in the Introduction, the Cauchy problem
We obtain from the Cauchy–Lipschitz theorem that problem (2.1) has a unique positive solution $F(\cdot ;\beta )\in C^2([0,\,\xi _{\max }(\beta )))$![]() defined on a maximal existence interval for which we have the following alternative: either $\xi _{\max }(\beta )=\infty$
defined on a maximal existence interval for which we have the following alternative: either $\xi _{\max }(\beta )=\infty$![]() or
or
We next define
and
We readily notice from (2.1a) and the $C^2$![]() -regularity of $F$
-regularity of $F$![]() that
that
so that $\xi _1(\beta )>0$![]() . Let us now study more precisely the behaviour of $F(\cdot ;\beta )$
. Let us now study more precisely the behaviour of $F(\cdot ;\beta )$![]() near $\xi _0(\beta )$
near $\xi _0(\beta )$![]() when $\xi _0(\beta )$
when $\xi _0(\beta )$![]() is finite.
is finite.
Lemma 2.1 Consider $\beta >0$![]() such that $\xi _0(\beta )<\infty$
such that $\xi _0(\beta )<\infty$![]() . Then $\xi _{\max }(\beta )=\xi _0(\beta )$
. Then $\xi _{\max }(\beta )=\xi _0(\beta )$![]() and $F=F(\cdot ;\beta )\in C^1([0,\,\xi _0(\beta )])$
and $F=F(\cdot ;\beta )\in C^1([0,\,\xi _0(\beta )])$![]() satisfies $F(\xi _0(\beta ))=0$
satisfies $F(\xi _0(\beta ))=0$![]() and
and
recalling that $f=F^{1/m}$![]() . Furthermore, if $\xi _0(\beta )=\xi _1(\beta )$
. Furthermore, if $\xi _0(\beta )=\xi _1(\beta )$![]() and $F'(\xi _0(\beta ))=0$
and $F'(\xi _0(\beta ))=0$![]() , then the extension of $F$
, then the extension of $F$![]() by zero on $(\xi _0(\beta ),\,\infty )$
by zero on $(\xi _0(\beta ),\,\infty )$![]() belongs to $C^2([0,\,\infty ))$
belongs to $C^2([0,\,\infty ))$![]() and is a solution to (2.1) on $[0,\,\infty )$
and is a solution to (2.1) on $[0,\,\infty )$![]() with
with
Also, the extension of $f$![]() by zero on $(\xi _0(\beta ),\,\infty )$
by zero on $(\xi _0(\beta ),\,\infty )$![]() belongs to $C^1([0,\,\infty ))$
belongs to $C^1([0,\,\infty ))$![]() .
.
Proof. As $\xi _0(\beta )<\infty$![]() , then the above alternative implies that $\xi _{\max }(\beta )=\xi _0(\beta )$
, then the above alternative implies that $\xi _{\max }(\beta )=\xi _0(\beta )$![]() and
and
Moreover, it follows from (2.1a) that
for $\xi \in [0,\,\xi _0(\beta ))$![]() ; hence, after integration over $(0,\,\xi )$
; hence, after integration over $(0,\,\xi )$![]() ,
,
Since we have already established in (2.5) that $F$![]() and $f$
and $f$![]() have a continuous extension on $[0,\,\xi _0(\beta )]$
have a continuous extension on $[0,\,\xi _0(\beta )]$![]() , we may take the limit $\xi \to \xi _0(\beta )$
, we may take the limit $\xi \to \xi _0(\beta )$![]() in the above identity and complete the proof of the first statement of lemma 2.1.
in the above identity and complete the proof of the first statement of lemma 2.1.
Now, assuming that $\xi _0(\beta )=\xi _1(\beta )$![]() and $F'(\xi _0(\beta ))=0$
and $F'(\xi _0(\beta ))=0$![]() , we integrate identity (2.6) over $(\xi,\,\xi _0(\beta ))$
, we integrate identity (2.6) over $(\xi,\,\xi _0(\beta ))$![]() and find
and find

for $\xi \in (0,\,\xi _0(\beta ))$![]() . Owing to the non-negativity of $f$
. Owing to the non-negativity of $f$![]() and $-F'$
and $-F'$![]() on $(0,\,\xi _0(\beta ))$
on $(0,\,\xi _0(\beta ))$![]() , we further obtain
, we further obtain

for $\xi \in (0,\,\xi _0(\beta ))$![]() . Since $f(\xi _0(\beta ))=0$
. Since $f(\xi _0(\beta ))=0$![]() , the right-hand side of the above inequality converges to zero as $\xi \nearrow \xi _0(\beta )$
, the right-hand side of the above inequality converges to zero as $\xi \nearrow \xi _0(\beta )$![]() and we conclude that $F''(\xi _0(\beta ))$
and we conclude that $F''(\xi _0(\beta ))$![]() is well-defined and equal to zero. Therefore, the extension of $F$
is well-defined and equal to zero. Therefore, the extension of $F$![]() by zero on $(\xi _0(\beta ),\,\infty )$
by zero on $(\xi _0(\beta ),\,\infty )$![]() is a $C^2$
is a $C^2$![]() -smooth function on $[0,\,\infty )$
-smooth function on $[0,\,\infty )$![]() , as claimed. Similarly, for $\xi \in (0,\,\xi _0(\beta ))$
, as claimed. Similarly, for $\xi \in (0,\,\xi _0(\beta ))$![]() ,
,

from which we deduce that $f'(\xi _0(\beta ))$![]() is well-defined and equal to zero. Hence, the extension of $f$
is well-defined and equal to zero. Hence, the extension of $f$![]() by zero on $(\xi _0(\beta ),\,\infty )$
by zero on $(\xi _0(\beta ),\,\infty )$![]() belongs to $C^1([0,\,\infty ))$
belongs to $C^1([0,\,\infty ))$![]() .
.
We now introduce the following three sets:

and observe that $\mathcal {A}\cap \mathrm {C}=\emptyset$![]() . Let us first show that the sets $\mathcal {A}$
. Let us first show that the sets $\mathcal {A}$![]() and $\mathcal {C}$
and $\mathcal {C}$![]() are non-empty and open.
are non-empty and open.
Lemma 2.2 The set $\mathcal {A}$![]() is non-empty and open and there exists $\beta _u>0$
is non-empty and open and there exists $\beta _u>0$![]() such that $(\beta _u,\,\infty )\subseteq \mathcal {A}$
such that $(\beta _u,\,\infty )\subseteq \mathcal {A}$![]() .
.
Proof. Set $g(\xi ;\beta )=f(\xi /\sqrt {\beta };\beta )$![]() for $\xi \in [0,\,\sqrt {\beta } \xi _0(\beta )]$
for $\xi \in [0,\,\sqrt {\beta } \xi _0(\beta )]$![]() , or equivalently $f(\xi ;\beta )=g(\xi \sqrt {\beta };\beta )$
, or equivalently $f(\xi ;\beta )=g(\xi \sqrt {\beta };\beta )$![]() for $\xi \in [0,\,\xi _0(\beta )]$
for $\xi \in [0,\,\xi _0(\beta )]$![]() . Setting also $G:=g^m$
. Setting also $G:=g^m$![]() , we obtain by straightforward calculations that $g$
, we obtain by straightforward calculations that $g$![]() (and thus $G$
(and thus $G$![]() ) solves the Cauchy problem
) solves the Cauchy problem
where $\zeta =\xi \sqrt {\beta }$![]() . Noticing that in the limit $\beta \to \infty$
. Noticing that in the limit $\beta \to \infty$![]() the last term in (2.7a) vanishes, we proceed exactly as in the proof of [Reference Iagar, Laurençot and Sánchez21, lemma 4.4] (see also the proof of [Reference Shi36, theorem 2] from where the idea comes) to conclude that there exists $\beta _u>0$
the last term in (2.7a) vanishes, we proceed exactly as in the proof of [Reference Iagar, Laurençot and Sánchez21, lemma 4.4] (see also the proof of [Reference Shi36, theorem 2] from where the idea comes) to conclude that there exists $\beta _u>0$![]() such that $(\beta _u,\,\infty )\subseteq \mathcal {A}$
such that $(\beta _u,\,\infty )\subseteq \mathcal {A}$![]() . We omit here the details as they are totally similar to the ones in the quoted references. That $\mathcal {A}$
. We omit here the details as they are totally similar to the ones in the quoted references. That $\mathcal {A}$![]() is open is an immediate consequence of the continuous dependence of $f(\cdot ;\beta )$
is open is an immediate consequence of the continuous dependence of $f(\cdot ;\beta )$![]() on $\beta$
on $\beta$![]() .
.
As for the set $\mathcal {C}$![]() , we do not need a rescaling in order to prove that it is non-empty.
, we do not need a rescaling in order to prove that it is non-empty.
Lemma 2.3 The set $\mathcal {C}$![]() is non-empty and open and there exists $\beta _l>0$
is non-empty and open and there exists $\beta _l>0$![]() such that $(0,\,\beta _l)\subseteq \mathcal {C}$
such that $(0,\,\beta _l)\subseteq \mathcal {C}$![]() .
.
Proof. We obtain by letting $\beta \to 0$![]() in (2.1) that the limit equation is
in (2.1) that the limit equation is
with initial conditions
By the Cauchy–Lipschitz theorem, problem (2.8) has a unique positive solution $H\in C^2([0,\,\xi _H))$![]() defined on a maximal existence interval for which we have the following alternative: either $\xi _H=\infty$
defined on a maximal existence interval for which we have the following alternative: either $\xi _H=\infty$![]() or
or
It follows from (2.8) that
Hence $\xi ^{N-1}H'(\xi )>0$![]() and thus $H'(\xi )>0$
and thus $H'(\xi )>0$![]() for any $\xi \in (0,\,\xi _H)$
for any $\xi \in (0,\,\xi _H)$![]() . Given $\delta \in (0,\,\xi _H)$
. Given $\delta \in (0,\,\xi _H)$![]() fixed, we have $H'(\delta )>0$
fixed, we have $H'(\delta )>0$![]() and $H(\xi )>1$
and $H(\xi )>1$![]() for any $\xi \in (0,\,\delta )$
for any $\xi \in (0,\,\delta )$![]() . The continuous dependence with respect to the parameter $\beta$
. The continuous dependence with respect to the parameter $\beta$![]() in (2.1) ensures that there exists $\beta _l>0$
in (2.1) ensures that there exists $\beta _l>0$![]() such that
such that
for any $\beta \in (0,\,\beta _l)$![]() . Recalling (2.2) and (2.3), we conclude that $\xi _1(\beta )\in (0,\,\delta )$
. Recalling (2.2) and (2.3), we conclude that $\xi _1(\beta )\in (0,\,\delta )$![]() and $\xi _0(\beta )>\delta$
and $\xi _0(\beta )>\delta$![]() for any $\beta \in (0,\,\beta _l)$
for any $\beta \in (0,\,\beta _l)$![]() ; that is, $\xi _1(\beta )<\xi _0(\beta )$
; that is, $\xi _1(\beta )<\xi _0(\beta )$![]() for $\beta \in (0,\,\beta _l)$
for $\beta \in (0,\,\beta _l)$![]() and $(0,\,\beta _l)\subseteq \mathcal {C}$
and $(0,\,\beta _l)\subseteq \mathcal {C}$![]() . We use once more the continuous dependence with respect to the parameter $\beta$
. We use once more the continuous dependence with respect to the parameter $\beta$![]() of $F(\cdot ;\beta )$
of $F(\cdot ;\beta )$![]() to conclude that $\mathcal {C}$
to conclude that $\mathcal {C}$![]() is open.
is open.
We infer from lemmas 2.2 and 2.3 that the set $\mathcal {B}$![]() is non-empty and closed. The instantaneous shrinking of supports of bounded solutions to equation (1.1) proved in [Reference Iagar, Laurençot and Sánchez21, theorem 1.1], together with the definition of the set $\mathcal {A}$
is non-empty and closed. The instantaneous shrinking of supports of bounded solutions to equation (1.1) proved in [Reference Iagar, Laurençot and Sánchez21, theorem 1.1], together with the definition of the set $\mathcal {A}$![]() , readily gives the following characterization of the elements in the set $\mathcal {B}$
, readily gives the following characterization of the elements in the set $\mathcal {B}$![]() .
.
Lemma 2.4 Let $\beta \in \mathcal {B}$![]() . Then $\xi _0(\beta )=\xi _1(\beta )<\infty$
. Then $\xi _0(\beta )=\xi _1(\beta )<\infty$![]() and $(f^m)'(\xi _0(\beta );\beta )=0$
and $(f^m)'(\xi _0(\beta );\beta )=0$![]() .
.
The proof is immediate and is given with details in [Reference Iagar, Laurençot and Sánchez21, lemma 4.6]. We thus conclude that, for any element $\beta \in \mathcal {B}$![]() , we have an eternal self-similar solution to equation (1.1) in form (1.4) with profile $f(\cdot ;\beta )$
, we have an eternal self-similar solution to equation (1.1) in form (1.4) with profile $f(\cdot ;\beta )$![]() as in lemma 2.4.
as in lemma 2.4.
2.2 Monotonicity
In this section, we prove the following general monotonicity property of the profiles $f(\cdot ;\beta )$![]() solving (2.1) with respect to the parameter $\beta$
solving (2.1) with respect to the parameter $\beta$![]() .
.
Lemma 2.5 Let $0<\beta _1<\beta _2<\infty$![]() . Then
. Then
Proof. Consider $\beta _2>\beta _1>0$![]() and pick $X\in (0,\,\min \{\xi _1(\beta _1),\, \xi _1(\beta _2)\})$
and pick $X\in (0,\,\min \{\xi _1(\beta _1),\, \xi _1(\beta _2)\})$![]() . Then
. Then
Since $\beta _2>\beta _1$![]() and $F_1(0)=F_2(0)=1$
and $F_1(0)=F_2(0)=1$![]() , $F_1'(0)=F_2'(0)=0$
, $F_1'(0)=F_2'(0)=0$![]() , we infer from (2.4) that $F_2< F_1$
, we infer from (2.4) that $F_2< F_1$![]() in a right-neighbourhood of $\xi =0$
in a right-neighbourhood of $\xi =0$![]() . We may thus define
. We may thus define
and notice that $F_2(\xi )< F_1(\xi )$![]() for any $\xi \in (0,\,\xi _*)$
for any $\xi \in (0,\,\xi _*)$![]() . Assume for contradiction that $\xi _*< X$
. Assume for contradiction that $\xi _*< X$![]() . Then $F_2(\xi _*)=F_1(\xi _*)$
. Then $F_2(\xi _*)=F_1(\xi _*)$![]() . We introduce for any $\lambda \geq 1$
. We introduce for any $\lambda \geq 1$![]() the following family of rescaled functions
the following family of rescaled functions
which are also solutions to (2.1a) with $\beta =\beta _2$![]() , and adapt an optimal barrier argument from [Reference Ye and Yin37] (see also [Reference Iagar, Laurençot and Sánchez21, lemma 4.12]). Owing to the monotonicity of $F_1$
, and adapt an optimal barrier argument from [Reference Ye and Yin37] (see also [Reference Iagar, Laurençot and Sánchez21, lemma 4.12]). Owing to the monotonicity of $F_1$![]() and $F_2$
and $F_2$![]() on $[0,\,X]$
on $[0,\,X]$![]() , we first note that
, we first note that
whence
while $F_1(\xi )\leq 1$![]() for $\xi \in [0,\,\xi _*]$
for $\xi \in [0,\,\xi _*]$![]() . Consequently, the optimal parameter
. Consequently, the optimal parameter
is well defined and finite. Since $F_2< F_1$![]() on $(0,\,\xi _*)$
on $(0,\,\xi _*)$![]() , we also deduce that $\lambda _0>1$
, we also deduce that $\lambda _0>1$![]() . The definition of $\lambda _0$
. The definition of $\lambda _0$![]() guarantees that there exists $\eta \in [0,\,\xi _*]$
guarantees that there exists $\eta \in [0,\,\xi _*]$![]() such that
such that
On the one hand, we infer from the monotonicity of $F_2$![]() and the property $\lambda _0>1$
and the property $\lambda _0>1$![]() that
that
which rules out the possibility that $\eta =\xi _*$![]() . On the other hand,
. On the other hand,
so that $\eta >0$![]() . Consequently, $\eta \in (0,\,\xi _*)$
. Consequently, $\eta \in (0,\,\xi _*)$![]() and we derive from (2.11) that $G_{\lambda _0}-F_1$
and we derive from (2.11) that $G_{\lambda _0}-F_1$![]() attains a strict minimum at $\xi =\eta$
attains a strict minimum at $\xi =\eta$![]() , which, together with the definition of $\eta$
, which, together with the definition of $\eta$![]() , implies that
, implies that
Since both $G_{\lambda _0}$![]() and $F_1$
and $F_1$![]() are solutions to (2.1a) with parameters $\beta _2$
are solutions to (2.1a) with parameters $\beta _2$![]() and $\beta _1$
and $\beta _1$![]() , respectively, we infer from (2.12) that
, respectively, we infer from (2.12) that

which leads to a contradiction. We have thus established that $F_2< F_1$![]() on $(0,\,X)$
on $(0,\,X)$![]() and the proof is complete due to the arbitrary choice of $X\in (0,\,\xi _1(\beta _2))\cap (0,\,\xi _1(\beta _1))$
and the proof is complete due to the arbitrary choice of $X\in (0,\,\xi _1(\beta _2))\cap (0,\,\xi _1(\beta _1))$![]() .
.
Let us remark that, in contrast to the range $\sigma >\sigma _c$![]() studied in [Reference Iagar, Laurençot and Sánchez21, § 3], in our case the profiles $f(\cdot ;\beta )$
studied in [Reference Iagar, Laurençot and Sánchez21, § 3], in our case the profiles $f(\cdot ;\beta )$![]() are ordered in a decreasing way with respect to the shooting parameter $\beta$
are ordered in a decreasing way with respect to the shooting parameter $\beta$![]() .
.
2.3 Interface behaviour
The goal of this section is deriving the local behaviour near the interface point $\xi _0(\beta )$![]() for profiles $f(\cdot ;\beta )$
for profiles $f(\cdot ;\beta )$![]() with $\beta \in \mathcal {B}$
with $\beta \in \mathcal {B}$![]() . We begin with a formal calculation. Let us drop for simplicity $\beta$
. We begin with a formal calculation. Let us drop for simplicity $\beta$![]() from the notation and assume that, at the interface, we have
from the notation and assume that, at the interface, we have
for some $A>0$![]() and $\theta >0$
and $\theta >0$![]() to be determined. We also obtain formally that
to be determined. We also obtain formally that
both equivalences holding true as $\xi \to \xi _0$![]() . Inserting this ansatz in (1.6) gives, as $\xi \to \xi _0$
. Inserting this ansatz in (1.6) gives, as $\xi \to \xi _0$![]() ,
,

We thus have four possibilities of balancing the dominating powers.
• $m\theta -2=\theta -1< q\theta$
 . This implies $\theta =1/(m-1)$
. This implies $\theta =1/(m-1)$ , but in this case $m\theta -1=\theta >0$
, but in this case $m\theta -1=\theta >0$ and thus this choice leads to $A=0$
and thus this choice leads to $A=0$ .
.• $\theta -1=q\theta < m\theta -2$
 . This implies $\theta =1/(1-q)$
. This implies $\theta =1/(1-q)$ and $m\theta -2>q\theta$
and $m\theta -2>q\theta$ leads straightforwardly to $m+q>2$
leads straightforwardly to $m+q>2$ .
.• $m\theta -2=q\theta <\theta -1$
 . This implies $\theta =2/(m-q)$
. This implies $\theta =2/(m-q)$ and the inequality $\theta -1>q\theta$
and the inequality $\theta -1>q\theta$ easily gives $m+q<2$
easily gives $m+q<2$ .
.• $m\theta -2=q\theta =\theta -1$
 . This implies that $\theta =1/(m-1)=1/(1-q)$
. This implies that $\theta =1/(m-1)=1/(1-q)$ and ${m+q=2}$
and ${m+q=2}$ .
.
Looking now at the constant $A$![]() in front of the previous ansatz, we find the following three cases:
in front of the previous ansatz, we find the following three cases:
Case 1. $m+q>2$![]() . According to the formal calculation, we expect $\theta =1/(1-q)$
. According to the formal calculation, we expect $\theta =1/(1-q)$![]() and then $\beta \xi _0 A\theta =A^q\xi _0^{\sigma }$
and then $\beta \xi _0 A\theta =A^q\xi _0^{\sigma }$![]() , which leads to
, which leads to
Case 2. $m+q=2$![]() . We expect $\theta =1/(1-q)=2/(m-q)$
. We expect $\theta =1/(1-q)=2/(m-q)$![]() and
and
that is, $A=A_*$![]() with $A_*$
with $A_*$![]() being the unique positive solution to
being the unique positive solution to
Since $m+q=2$![]() and $\sigma =2$
and $\sigma =2$![]() in that case, the above equation simplifies to
in that case, the above equation simplifies to
Case 3. $m+q<2$![]() . We expect $\theta =2/(m-q)$
. We expect $\theta =2/(m-q)$![]() and $m\theta (m\theta -1)A^m=A^q\xi _0^{\sigma }$
and $m\theta (m\theta -1)A^m=A^q\xi _0^{\sigma }$![]() , hence
, hence
In order to prove in a rigorous way all these estimates near the interface, we proceed as in [Reference Iagar, Laurençot and Sánchez21]. We start with some general upper bounds at the interface, but omit the proof, as it is totally similar to that of [Reference Iagar, Laurençot and Sánchez21, lemma 4.7].
Lemma 2.6 Assume that $\beta \in \mathcal {B}$![]() and set $f=f(\cdot ;\beta )$
and set $f=f(\cdot ;\beta )$![]() and $\xi _0=\xi _0(\beta )$
and $\xi _0=\xi _0(\beta )$![]() . Then
. Then
and
Moreover, there exists $C_1>0$![]() depending only on $N$
depending only on $N$![]() , $m$
, $m$![]() and $q$
and $q$![]() such that
such that
The following consequences of lemma 2.6 are drawn in the same way as in [Reference Iagar, Laurençot and Sánchez21, lemmas 4.8 and 4.9].
Corollary 2.7 Let $\beta \in \mathcal {B}$![]() and set $f=f(\cdot ;\beta )$
and set $f=f(\cdot ;\beta )$![]() and $\xi _0=\xi _0(\beta )$
and $\xi _0=\xi _0(\beta )$![]() . Then
. Then
In addition, if $m+q>2$![]() then
then
The estimates given in corollary 2.7 allow us to proceed as in [Reference Iagar, Laurençot and Sánchez21, propositions 4.10 and 4.11] in order to identify the precise algebraic rate at which $f(\cdot ;\beta )$![]() vanishes at the interface, which depends on the sign of $m+q-2$
vanishes at the interface, which depends on the sign of $m+q-2$![]() as follows.
as follows.
Proposition 2.8 Let $\beta \in \mathcal {B}$![]() and set $f=f(\cdot ;\beta )$
and set $f=f(\cdot ;\beta )$![]() and $\xi _0=\xi _0(\beta )$
and $\xi _0=\xi _0(\beta )$![]() .
.
(a) If $m+q<2$![]() , then, as $\xi \to \xi _0$
, then, as $\xi \to \xi _0$![]() ,
,
where

(b) If $m+q=2$![]() , then $\sigma =2$
, then $\sigma =2$![]() and, as $\xi \to \xi _0$
and, as $\xi \to \xi _0$![]() ,
,
where $K_1$![]() is defined in part (a) and
is defined in part (a) and

(c) If $m+q>2$![]() , then, as $\xi \to \xi _0$
, then, as $\xi \to \xi _0$![]() ,
,
where

Let us notice here that the values of $K_1$![]() , $K_2(\beta )$
, $K_2(\beta )$![]() and $K_3(\beta )$
and $K_3(\beta )$![]() in (2.19), (2.20) and (2.21) correspond to the values of $A$
in (2.19), (2.20) and (2.21) correspond to the values of $A$![]() obtained through the formal deduction in (2.15), (2.14) and (2.13), respectively. It is now worth pointing out that there is no explicit dependence on $\beta$
obtained through the formal deduction in (2.15), (2.14) and (2.13), respectively. It is now worth pointing out that there is no explicit dependence on $\beta$![]() in the behaviour (2.19) when $m+q<2$
in the behaviour (2.19) when $m+q<2$![]() . This is why we need to perform some rather serious extra work in order to identify the second order of the expansion at the interface when $m+q\in (1,\,2)$
. This is why we need to perform some rather serious extra work in order to identify the second order of the expansion at the interface when $m+q\in (1,\,2)$![]() , as formal computations (which are rather tedious and we do not give here) reveal that $\beta$
, as formal computations (which are rather tedious and we do not give here) reveal that $\beta$![]() shows up in an explicit way in this next order, a feature that will be very helpful in the proof of the uniqueness issue. More precisely, we have the following asymptotic expansions.
shows up in an explicit way in this next order, a feature that will be very helpful in the proof of the uniqueness issue. More precisely, we have the following asymptotic expansions.
Proposition 2.9 Let $m+q<2$![]() , $\beta \in \mathcal {B}$
, $\beta \in \mathcal {B}$![]() and set $f=f(\cdot ;\beta )$
and set $f=f(\cdot ;\beta )$![]() and $\xi _0=\xi _0(\beta )$
and $\xi _0=\xi _0(\beta )$![]() . Then, as $\xi \to \xi _0$
. Then, as $\xi \to \xi _0$![]() ,
,

where $K_1$![]() is defined in (2.19) and
is defined in (2.19) and
Proof. As in the proof of [Reference Iagar, Laurençot and Sánchez21, proposition 4.10], we introduce the new dependent variables

as well as a new independent variable $\eta$![]() via the integral representation
via the integral representation
Introducing $(X,\,Y,\,Z)$![]() defined by $(\mathcal {X},\,\mathcal {Y},\,\mathcal {Z})=(X\circ \eta,\,Y\circ \eta,\,Z\circ \eta )$
defined by $(\mathcal {X},\,\mathcal {Y},\,\mathcal {Z})=(X\circ \eta,\,Y\circ \eta,\,Z\circ \eta )$![]() , we see that $(X,\,Y,\,Z)$
, we see that $(X,\,Y,\,Z)$![]() solves the quadratic autonomous dynamical system
solves the quadratic autonomous dynamical system

Observe that, owing to (2.19),
so that studying the behaviour of $(\mathcal {X},\,\mathcal {Y},\,\mathcal {Z})(\xi )$![]() as $\xi \to \xi _0$
as $\xi \to \xi _0$![]() amounts to that of $(X,\,Y,\,Z)(\eta )$
amounts to that of $(X,\,Y,\,Z)(\eta )$![]() as $\eta \to \infty$
as $\eta \to \infty$![]() . Furthermore, we argue as in [Reference Iagar, Laurençot and Sánchez21, proposition 4.10] to deduce from (2.19) and corollary 2.7 that
. Furthermore, we argue as in [Reference Iagar, Laurençot and Sánchez21, proposition 4.10] to deduce from (2.19) and corollary 2.7 that
and
We are thus interested in the behaviour near the critical point $(0,\,-\sqrt {2/(m+q)},\,0)$![]() . We translate this point to the origin of coordinates by setting
. We translate this point to the origin of coordinates by setting
We then find by direct calculation that system (2.26) becomes

Introducing $\mathbf {F}(\mathbf {V}) = (F_1,\,F_2,\,F_3)(\mathbf {V})$![]() defined for $\mathbf {V}=(V_1,\,V_2,\,V_3)\in \mathbb {R}^3$
defined for $\mathbf {V}=(V_1,\,V_2,\,V_3)\in \mathbb {R}^3$![]() by
by

and denoting the semiflow associated with the dynamical system
by $\varphi (\cdot ;\mathbf {V}_0)$![]() , we deduce from (2.28) that $\mathbf {V}_* := (X,\,W,\,Z) = \varphi (\cdot ;\mathbf {V}_*(0))$
, we deduce from (2.28) that $\mathbf {V}_* := (X,\,W,\,Z) = \varphi (\cdot ;\mathbf {V}_*(0))$![]() is defined on $[0,\,\infty )$
is defined on $[0,\,\infty )$![]() with
with
The matrix associated with the linearization of system (2.29) at the origin is

having three distinct eigenvalues
with corresponding eigenvectors (not normalized)
Then $\mathbf {0}$![]() is a hyperbolic point of $\varphi$
is a hyperbolic point of $\varphi$![]() and has a two-dimensional stable manifold $\mathcal {W}_s(\mathbf {0})$
and has a two-dimensional stable manifold $\mathcal {W}_s(\mathbf {0})$![]() . According to the proof of the stable manifold theorem (see e.g. [Reference Amann2, theorem 19.11]), there is an open neighbourhood $\mathcal {V}$
. According to the proof of the stable manifold theorem (see e.g. [Reference Amann2, theorem 19.11]), there is an open neighbourhood $\mathcal {V}$![]() of zero in $\mathbb {R}^3$
of zero in $\mathbb {R}^3$![]() , an open neighbourhood $\mathcal {V}_0$
, an open neighbourhood $\mathcal {V}_0$![]() of zero in $\mathbb {R}^2$
of zero in $\mathbb {R}^2$![]() and a $C^2$
and a $C^2$![]() -smooth function $h:\mathcal {V}_0\to \mathbb {R}$
-smooth function $h:\mathcal {V}_0\to \mathbb {R}$![]() such that $h(0,\,0)=\partial _x h(0,\,0)=\partial _z h(0,\,0)=0$
such that $h(0,\,0)=\partial _x h(0,\,0)=\partial _z h(0,\,0)=0$![]() and the local stable manifold
and the local stable manifold
satisfies
its tangent space at $\mathbf {0}$![]() being $\mathbb {R} E_1 \oplus \mathbb {R} E_3$
being $\mathbb {R} E_1 \oplus \mathbb {R} E_3$![]() . Since $\{\varphi (\eta ;\mathbf {V}_*(0))\ : \ \eta \geq \eta _0\}$
. Since $\{\varphi (\eta ;\mathbf {V}_*(0))\ : \ \eta \geq \eta _0\}$![]() is included in $\mathcal {W}_s(\mathbf {0})\cap \mathcal {V}$
is included in $\mathcal {W}_s(\mathbf {0})\cap \mathcal {V}$![]() for $\eta _0$
for $\eta _0$![]() large enough by (2.30), we conclude that $\varphi (\eta ;\mathbf {V}_*(0))$
large enough by (2.30), we conclude that $\varphi (\eta ;\mathbf {V}_*(0))$![]() belongs to $\mathcal {W}_s^{\mathcal {V}}(\mathbf {0})$
belongs to $\mathcal {W}_s^{\mathcal {V}}(\mathbf {0})$![]() for $\eta \ge \eta _0$
for $\eta \ge \eta _0$![]() . Consequently, there are functions $(\overline {x},\,\overline {z}):[\eta _0,\,\infty )\to \mathcal {V}_0$
. Consequently, there are functions $(\overline {x},\,\overline {z}):[\eta _0,\,\infty )\to \mathcal {V}_0$![]() such that
such that
for $\eta \geq \eta _0$![]() . In fact, $\overline {x}(\eta )=X(\eta )$
. In fact, $\overline {x}(\eta )=X(\eta )$![]() , $\overline {z}(\eta )=Z(\eta )$
, $\overline {z}(\eta )=Z(\eta )$![]() and
and
Let us notice from (2.24) that
which implies that $X(\eta )=o(Z(\eta ))$![]() as $\eta \to \infty$
as $\eta \to \infty$![]() , since $(2-m-q)/(m-q)<1$
, since $(2-m-q)/(m-q)<1$![]() . Recalling also that $h$
. Recalling also that $h$![]() is $C^2$
is $C^2$![]() -smooth with $h(0,\,0)=\partial _x h(0,\,0)=\partial _z h(0,\,0)=0$
-smooth with $h(0,\,0)=\partial _x h(0,\,0)=\partial _z h(0,\,0)=0$![]() , we infer from (2.31) that
, we infer from (2.31) that
or equivalently, undoing the change of variable (2.25) and the translation (2.27), we get as $\xi \to \xi _0$![]() ,
,
Moreover, we readily infer from the already obtained local behaviour (2.19) and the definition of $\mathcal {Z}$![]() in (2.24) that, as $\xi \to \xi _0$
in (2.24) that, as $\xi \to \xi _0$![]() ,
,
Inserting the previous expansion into (2.32) and recalling the definition of $\mathcal {Y}$![]() in (2.24), we find
in (2.24), we find

which leads to, since $\alpha =2\beta /(m-1)$![]() ,
,

Recalling that $(2-m-q)/(m-q)<1$![]() , we end up with
, we end up with

Integrating (2.33) over $(\xi,\,\xi _0)$![]() and then taking powers $2/(m-q)$
and then taking powers $2/(m-q)$![]() give
give

as stated.
2.4 Uniqueness
We are now ready to complete the proof of theorem 1.1 by showing that the set $\mathcal {B}$![]() contains at most one element. Taking into account the previous preparations, this proof borrows ideas from the analogous one in [Reference Iagar, Laurençot and Sánchez21, § 4.4].
contains at most one element. Taking into account the previous preparations, this proof borrows ideas from the analogous one in [Reference Iagar, Laurençot and Sánchez21, § 4.4].
Proof. Proof of theorem 1.1: uniqueness
Assume for contradiction that there are $\beta _1\in \mathcal {B}$![]() and $\beta _2\in \mathcal {B}$
and $\beta _2\in \mathcal {B}$![]() such that $0<\beta _1<\beta _2<\infty$
such that $0<\beta _1<\beta _2<\infty$![]() . By lemma 2.4, we have $\xi _0(\beta _1)=\xi _1(\beta _1)$
. By lemma 2.4, we have $\xi _0(\beta _1)=\xi _1(\beta _1)$![]() and $\xi _0(\beta _2)=\xi _1(\beta _2)$
and $\xi _0(\beta _2)=\xi _1(\beta _2)$![]() , so that lemma 2.5 implies that $f_1(\xi )>f_2(\xi )$
, so that lemma 2.5 implies that $f_1(\xi )>f_2(\xi )$![]() and $F_1(\xi )>F_2(\xi )$
and $F_1(\xi )>F_2(\xi )$![]() for any $\xi \in (0,\,\min \{\xi _0(\beta _1),\,\xi _0(\beta _2)\})$
for any $\xi \in (0,\,\min \{\xi _0(\beta _1),\,\xi _0(\beta _2)\})$![]() , with $f_i:=f(\cdot ;\beta _i)$
, with $f_i:=f(\cdot ;\beta _i)$![]() and $F_i:=f_i^m$
and $F_i:=f_i^m$![]() for $i=1,\,2$
for $i=1,\,2$![]() . In particular, $\xi _0(\beta _2)<\xi _0(\beta _1)$
. In particular, $\xi _0(\beta _2)<\xi _0(\beta _1)$![]() .
.
As in the proof of lemma 2.5, see (2.9)–(2.10), we introduce the rescaled version $G_\lambda$![]() of $F_2$
of $F_2$![]() defined by
defined by
recalling that $F_2$![]() is well-defined on $[0,\,\infty )$
is well-defined on $[0,\,\infty )$![]() by lemma 2.1, and define the optimal parameter
by lemma 2.1, and define the optimal parameter
its existence being ensured by the fact that

According to the definition of $\lambda _0$![]() in (2.35) and the compactness of the interval $[0,\,\xi _0(\beta _1)]$
in (2.35) and the compactness of the interval $[0,\,\xi _0(\beta _1)]$![]() , we deduce that there is $\eta \in [0,\,\xi _0(\beta _1)]$
, we deduce that there is $\eta \in [0,\,\xi _0(\beta _1)]$![]() such that $F_1(\eta )=G_{\lambda _0}(\eta )$
such that $F_1(\eta )=G_{\lambda _0}(\eta )$![]() and $F_1\leq G_{\lambda _0}$
and $F_1\leq G_{\lambda _0}$![]() on $[0,\,\xi _0(\beta _1)]$
on $[0,\,\xi _0(\beta _1)]$![]() . Arguments very similar to the ones employed in the proof of lemma 2.5, along with lemma 2.1, then discard the possibility that either $\eta =0$
. Arguments very similar to the ones employed in the proof of lemma 2.5, along with lemma 2.1, then discard the possibility that either $\eta =0$![]() or $\eta \in (0,\,\xi _0(\beta _1))$
or $\eta \in (0,\,\xi _0(\beta _1))$![]() , thus showing that $\eta =\xi _0(\beta _1)$
, thus showing that $\eta =\xi _0(\beta _1)$![]() . Consequently,
. Consequently,
and we also obtain the following equality implied by the equality of the supports in (2.36) and rescaling (2.34)
We now split the analysis into the three cases already set apart at the beginning of § 2.3, according to the sign of $m+q-2$![]() .
.
Case 1. $m+q<2$![]() . We recall that, in this case, proposition 2.9 gives
. We recall that, in this case, proposition 2.9 gives

as $\xi \to \xi _0(\beta _i)$![]() , $i=1,\,2$
, $i=1,\,2$![]() . In order to simplify the calculations, we can work at the level of $f_i$
. In order to simplify the calculations, we can work at the level of $f_i$![]() by noticing that rescaling (2.34) reduces to
by noticing that rescaling (2.34) reduces to
We thus infer from (2.38) and (2.39) that

Noticing that the powers of $\lambda _0$![]() appearing in the (rather tedious) previous calculations cancel out due to the precise value of $\sigma$
appearing in the (rather tedious) previous calculations cancel out due to the precise value of $\sigma$![]() given in (1.2), we further obtain
given in (1.2), we further obtain

Since $\beta _1<\beta _2$![]() , we deduce from (2.23) that $K_0(\beta _1)< K_0(\beta _2)$
, we deduce from (2.23) that $K_0(\beta _1)< K_0(\beta _2)$![]() . Thus, $g_{\lambda _0}(\xi )< f_1(\xi )$
. Thus, $g_{\lambda _0}(\xi )< f_1(\xi )$![]() in a left neighbourhood of $\xi _0(\beta _1)$
in a left neighbourhood of $\xi _0(\beta _1)$![]() , whence (by raising to power $m$
, whence (by raising to power $m$![]() ) $G_{\lambda _0}(\xi )< F_1(\xi )$
) $G_{\lambda _0}(\xi )< F_1(\xi )$![]() in the same left neighbourhood of $\xi _0(\beta _1)$
in the same left neighbourhood of $\xi _0(\beta _1)$![]() , and we have reached a contradiction to (2.36).
, and we have reached a contradiction to (2.36).
Case 2. $m+q=2$![]() . In this case, proposition 2.8 (b) gives
. In this case, proposition 2.8 (b) gives
as $\xi \to \xi _0(\beta _i)$![]() , $i=1,\,2$
, $i=1,\,2$![]() . We thus have
. We thus have

the powers of $\lambda _0$![]() cancelling out due to $m+q=2$
cancelling out due to $m+q=2$![]() . Noticing that we can write
. Noticing that we can write

we easily observe that $K_2$![]() is a decreasing function of $\beta$
is a decreasing function of $\beta$![]() , thus $K_2(\beta _2)< K_2(\beta _1)$
, thus $K_2(\beta _2)< K_2(\beta _1)$![]() since $\beta _2>\beta _1$
since $\beta _2>\beta _1$![]() . Therefore, $G_{\lambda _0}(\xi )< F_1(\xi )$
. Therefore, $G_{\lambda _0}(\xi )< F_1(\xi )$![]() in a left neighbourhood of $\xi _0(\beta _1)$
in a left neighbourhood of $\xi _0(\beta _1)$![]() , which contradicts (2.36).
, which contradicts (2.36).
Case 3. $m+q>2$![]() . We recall that, in this case, proposition 2.8 (c) gives
. We recall that, in this case, proposition 2.8 (c) gives
as $\xi \to \xi _0(\beta _i)$![]() , $i=1,\,2$
, $i=1,\,2$![]() . Using then rescaling (2.34) and identity (2.37), we readily infer that
. Using then rescaling (2.34) and identity (2.37), we readily infer that

Since $K_3(\beta _2)< K_3(\beta _1)$![]() for $\beta _2>\beta _1$
for $\beta _2>\beta _1$![]() , we find that $G_{\lambda _0}(\xi )< F_1(\xi )$
, we find that $G_{\lambda _0}(\xi )< F_1(\xi )$![]() in a left neighbourhood of $\xi _0(\beta _1)$
in a left neighbourhood of $\xi _0(\beta _1)$![]() , which is again a contradiction to (2.36).
, which is again a contradiction to (2.36).
The previous contradictions imply that there cannot be two different values of the exponent $\beta$![]() in the set $\mathcal {B}$
in the set $\mathcal {B}$![]() , completing the proof.
, completing the proof.
Acknowledgements
This work is partially supported by the Spanish project PID2020-115273GB-I00 and by the Grant RED2022-134301-T (Spain). Part of this work has been developed during visits of R. G. I. to Institut de Mathématiques de Toulouse and to Laboratoire de Mathématiques LAMA, Université de Savoie, and of P. L. to Universidad Rey Juan Carlos, and both authors thank these institutions for hospitality and support. The authors wish to thank Ariel Sánchez (Universidad Rey Juan Carlos) for interesting comments and suggestions. We also thank the referees for carefully reading the manuscript.