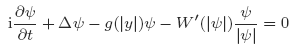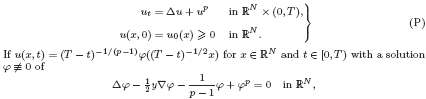Research Article
Motion by anisotropic mean curvature as sharp interface limit of an inhomogeneous and anisotropic Allen–Cahn equation
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 673-706
-
- Article
- Export citation
Nonlinear Schrödinger equations with strongly singular potentials
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 707-721
-
- Article
- Export citation
Characterization of higher-order monotonicity via integral inequalities
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 723-736
-
- Article
- Export citation
Infinitely many solutions for a Dirichlet problem involving the p-Laplacian
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 737-752
-
- Article
- Export citation
Unimodal wavetrains and solitons in convex Fermi–Pasta–Ulam chains
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 753-785
-
- Article
- Export citation
Hodge-Frobenius equations and the Hodge–Bäcklund transformation
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 787-819
-
- Article
- Export citation
On backward self-similar blow-up solutions to a supercritical semilinear heat equation
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 821-831
-
- Article
- Export citation
Large-time behaviour of solutions to non-Newtonian filtration equations with nonlinear boundary sources
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 833-855
-
- Article
- Export citation
Geometric Langlands duality and the equations of Nahm and Bogomolny
-
- Published online by Cambridge University Press:
- 04 August 2010, pp. 857-895
-
- Article
- Export citation