The characteristic properties of quadratic differential forms, involving two or more independent variables, have been investigated from the days of Gauss onwards. Initially, the discussion arose for the case of two variables; and, in its most general trend, it was concerned with a form
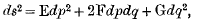
associated with surfaces, E, F, G being integral functions of p and q. But the relation does not, by itself, define a surface completely. When a surface is deformed in any manner, without stretching and without tearing, the quantity ds2 preserves its measure unchanged; the measure is of fundamental importance. Consequently, the measure must remain unchanged whatever changes of the variables are admitted. Further, changes of the variables, of any kind, allow the existence of covariant concomitants which therefore persist through these changes. In particular, there is one function, of E, F, G and of their derivatives up to the second order inclusive, which persists unaltered; it is the Gauss measure of the curvature of the surface.