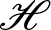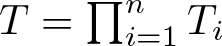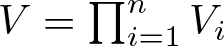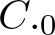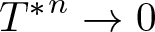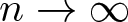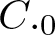1. Introduction
We consider only bounded operators acting on complex Hilbert spaces. A contraction is an operator with norm not greater than 1.
The aim of dilation, roughly speaking, is to realize a given tuple of commuting operators as a compression of an appropriate commuting tuple of normal operators. Let ![]() $(T_1, \dots, T_n)$ be a tuple of commuting contractions acting on a Hilbert space
$(T_1, \dots, T_n)$ be a tuple of commuting contractions acting on a Hilbert space ![]() $\mathscr{H}$. One would like to represent
$\mathscr{H}$. One would like to represent ![]() $(T_1, \dots, T_n)$ as a compression of an n-tuple of commuting unitaries or more precisely as a compression of an n-tuple of commuting isometries, because, every such tuple of commuting isometries extends naturally to a commuting tuple of unitaries. A commuting tuple of isometries
$(T_1, \dots, T_n)$ as a compression of an n-tuple of commuting unitaries or more precisely as a compression of an n-tuple of commuting isometries, because, every such tuple of commuting isometries extends naturally to a commuting tuple of unitaries. A commuting tuple of isometries ![]() $(V_1, \dots, V_n)$ acting on a Hilbert space
$(V_1, \dots, V_n)$ acting on a Hilbert space ![]() $\mathscr{K}$ is said to be an isometric dilation of
$\mathscr{K}$ is said to be an isometric dilation of ![]() $(T_1, \dots, T_n)$ if
$(T_1, \dots, T_n)$ if ![]() $\mathscr{H}$ can be identified as a closed linear subspace of
$\mathscr{H}$ can be identified as a closed linear subspace of ![]() $\mathscr{K}$, i.e.,
$\mathscr{K}$, i.e., ![]() $\mathscr{H} \subseteq \mathscr{K}$ and for any non-negative integers,
$\mathscr{H} \subseteq \mathscr{K}$ and for any non-negative integers, ![]() $k_1, \dots, k_n$
$k_1, \dots, k_n$
 \begin{equation*}
T_1^{k_1} \dots T_n^{k_n}=P_{\mathscr{H}} (V_1^{k_1}\dots V_n^{k_n})|_{\mathscr{H}},
\end{equation*}
\begin{equation*}
T_1^{k_1} \dots T_n^{k_n}=P_{\mathscr{H}} (V_1^{k_1}\dots V_n^{k_n})|_{\mathscr{H}},
\end{equation*} where ![]() $P_{\mathscr{H}}:\mathscr{K} \rightarrow \mathscr{H}$ is the orthogonal projection. Moreover, such an isometric dilation is called minimal if
$P_{\mathscr{H}}:\mathscr{K} \rightarrow \mathscr{H}$ is the orthogonal projection. Moreover, such an isometric dilation is called minimal if
 \begin{equation*}
\mathscr{K} = \overline{Span}\; \{V_1^{k_1}\dots V_n^{k_n}h\;:\; h\in \mathscr{H} , \; k_1, \dots, k_n \in \mathbb N \cup \{0 \} \}.
\end{equation*}
\begin{equation*}
\mathscr{K} = \overline{Span}\; \{V_1^{k_1}\dots V_n^{k_n}h\;:\; h\in \mathscr{H} , \; k_1, \dots, k_n \in \mathbb N \cup \{0 \} \}.
\end{equation*} If ![]() $(V_1, \dots, V_n)$ dilates
$(V_1, \dots, V_n)$ dilates ![]() $(T_1, \dots, T_n)$, then each Ti is a compression of Vi, that is,
$(T_1, \dots, T_n)$, then each Ti is a compression of Vi, that is, ![]() $T_i=P_{\mathscr{H}}V_i|_{\mathscr{H}}$. It is well-known that a contraction admits an isometric dilation (Sz. Nagy, [Reference Sz.-Nagy57]) and that a pair of commuting contractions always dilates to a pair of commuting isometries (Ando, [Reference Ando4]), though a triple of commuting contractions may or may not dilate to a triple of commuting isometries (Parrott, [Reference Parrott48]). In other words, rational dilation succeeds on the closed unit disk
$T_i=P_{\mathscr{H}}V_i|_{\mathscr{H}}$. It is well-known that a contraction admits an isometric dilation (Sz. Nagy, [Reference Sz.-Nagy57]) and that a pair of commuting contractions always dilates to a pair of commuting isometries (Ando, [Reference Ando4]), though a triple of commuting contractions may or may not dilate to a triple of commuting isometries (Parrott, [Reference Parrott48]). In other words, rational dilation succeeds on the closed unit disk ![]() $\overline{\mathbb D}$ and on the closed bidisc
$\overline{\mathbb D}$ and on the closed bidisc ![]() $\overline{\mathbb D}^2$ and fails on the closed polydisc
$\overline{\mathbb D}^2$ and fails on the closed polydisc ![]() $\overline{\mathbb{D}}^n$ when
$\overline{\mathbb{D}}^n$ when ![]() $n \geq 3$. Since a commuting tuple of contractions
$n \geq 3$. Since a commuting tuple of contractions ![]() $(T_1, \dots, T_n)$ does not dilate unconditionally whenever
$(T_1, \dots, T_n)$ does not dilate unconditionally whenever ![]() $n\geq 3$, efforts have been made to find classes of contractions that dilate under certain conditions and some remarkable works have been witnessed, e.g., Agler [Reference Agler1], Arveson [Reference Arveson8], Ball, Li, Timotin, and Trent [Reference Ball, Li, Timotin and Trent13], Ball, Trent, and Vinnikov [Reference Ball, Trent and Vinnikov14], Bhat, Bhattacharyya, and Dey [Reference Bhat, Bhattacharyya and Dey19], Binding, Farenick, and Li [Reference Binding, Farenick and Li22], Brehmer [Reference Brehmer23], Crabb and Davie [Reference Crabb and Davie26], Curto and Vasilescu [Reference Curto and Vasilescu27, Reference Curto and Vasilescu28], Dey [Reference Dey31], Grinshpan, Kaliuzhnyi-Verbovetki, Vinnikov, and Woerdeman [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36], Muller and Vasilescu [Reference Müller and Vasilescu46], Popescu [Reference Popescu53], and many others. See the references therein and also see §2 for further details.
$n\geq 3$, efforts have been made to find classes of contractions that dilate under certain conditions and some remarkable works have been witnessed, e.g., Agler [Reference Agler1], Arveson [Reference Arveson8], Ball, Li, Timotin, and Trent [Reference Ball, Li, Timotin and Trent13], Ball, Trent, and Vinnikov [Reference Ball, Trent and Vinnikov14], Bhat, Bhattacharyya, and Dey [Reference Bhat, Bhattacharyya and Dey19], Binding, Farenick, and Li [Reference Binding, Farenick and Li22], Brehmer [Reference Brehmer23], Crabb and Davie [Reference Crabb and Davie26], Curto and Vasilescu [Reference Curto and Vasilescu27, Reference Curto and Vasilescu28], Dey [Reference Dey31], Grinshpan, Kaliuzhnyi-Verbovetki, Vinnikov, and Woerdeman [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36], Muller and Vasilescu [Reference Müller and Vasilescu46], Popescu [Reference Popescu53], and many others. See the references therein and also see §2 for further details.
In this article, we consider the minimal isometric dilation space ![]() $\mathscr{K}$ (which is always unique up to unitary) of the product
$\mathscr{K}$ (which is always unique up to unitary) of the product ![]() $T=\prod_{i=1}^n T_i$ of a tuple commuting contractions
$T=\prod_{i=1}^n T_i$ of a tuple commuting contractions ![]() $(T_1, \dots, T_n)$ acting on
$(T_1, \dots, T_n)$ acting on ![]() $\mathscr{H}$. We find a necessary and sufficient condition such that
$\mathscr{H}$. We find a necessary and sufficient condition such that ![]() $(T_1, \dots, T_n)$ dilates to a commuting isometric tuple
$(T_1, \dots, T_n)$ dilates to a commuting isometric tuple ![]() $(V_1, \dots, V_n)$ on
$(V_1, \dots, V_n)$ on ![]() $\mathscr{K}$ with the product
$\mathscr{K}$ with the product ![]() $V=\prod_{i=1}^n V_i$ being the minimal isometric dilation of
$V=\prod_{i=1}^n V_i$ being the minimal isometric dilation of ![]() $T=\prod_{i=1}^n T_i$. Note that the space
$T=\prod_{i=1}^n T_i$. Note that the space ![]() $\mathscr{K}$ is unique in the sense that any two minimal isometric dilation spaces of the product T are unitarily equivalent. This is one of the main results in this article and is stated below.
$\mathscr{K}$ is unique in the sense that any two minimal isometric dilation spaces of the product T are unitarily equivalent. This is one of the main results in this article and is stated below.
Theorem 1.1 Let ![]() $T_1,\ldots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions and let
$T_1,\ldots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions and let ![]() $T={\prod_{i=1}^n T_i}$.
$T={\prod_{i=1}^n T_i}$.
(a) If
 $\mathscr{K}$ is the minimal isometric dilation space of T, then
$\mathscr{K}$ is the minimal isometric dilation space of T, then  $(T_1,\ldots,T_n)$ possesses an isometric dilation
$(T_1,\ldots,T_n)$ possesses an isometric dilation  $(V_1,\ldots,V_{n})$ on
$(V_1,\ldots,V_{n})$ on  $\mathscr{K}$ with
$\mathscr{K}$ with  $V=\Pi_{i=1}^nV_i$ being the minimal isometric dilation of T if and only if there are unique orthogonal projections
$V=\Pi_{i=1}^nV_i$ being the minimal isometric dilation of T if and only if there are unique orthogonal projections  $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries  $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in  $\mathscr{B}(\mathscr{D}_T)$ with
$\mathscr{B}(\mathscr{D}_T)$ with  $\prod_{i=1}^n U_i=I_{\mathscr{D}_{T}}$ such that the following conditions are satisfied for each
$\prod_{i=1}^n U_i=I_{\mathscr{D}_{T}}$ such that the following conditions are satisfied for each  $i=1, \dots, n$:
$i=1, \dots, n$:(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_TU_iP_iU_i^*D_T=D_{T_i}^2$,
$D_TU_iP_iU_i^*D_T=D_{T_i}^2$,(5)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
(b) Such an isometric dilation is minimal and unique in the sense that if
 $(W_1, \dots, W_n)$ on
$(W_1, \dots, W_n)$ on  $\mathscr{K}_1$ and
$\mathscr{K}_1$ and  $(Y_1, \dots, Y_n)$ on
$(Y_1, \dots, Y_n)$ on  $\mathscr{K}_2$ are two isometric dilations of
$\mathscr{K}_2$ are two isometric dilations of  $(T_1, \dots, T_n)$ such that
$(T_1, \dots, T_n)$ such that  $W=\prod_{i=1}^nW_i$ and
$W=\prod_{i=1}^nW_i$ and  $Y=\prod_{i=1}^nY_i$ are minimal isometric dilations of T on
$Y=\prod_{i=1}^nY_i$ are minimal isometric dilations of T on  $\mathscr{K}_1$ and
$\mathscr{K}_1$ and  $\mathscr{K}_2$, respectively, then there is a unitary
$\mathscr{K}_2$, respectively, then there is a unitary  $\widetilde{U}:\mathscr{K}_1 \rightarrow \mathscr{K}_2$ such that
$\widetilde{U}:\mathscr{K}_1 \rightarrow \mathscr{K}_2$ such that  $(W_1, \dots, W_n)=(\widetilde{U}^*Y_1\widetilde{U}, \dots, \widetilde{U}^*Y_n\widetilde{U})$.
$(W_1, \dots, W_n)=(\widetilde{U}^*Y_1\widetilde{U}, \dots, \widetilde{U}^*Y_n\widetilde{U})$.
This is Theorem 3.5 in this article and will be proved in §3. We show an explicit construction of a Schäffer-type minimal isometric dilation for ![]() $(T_1, \dots, T_n)$ on the space
$(T_1, \dots, T_n)$ on the space ![]() $\mathscr{K}= \mathscr{H} \oplus l^2(\mathscr{D}_T)$, where
$\mathscr{K}= \mathscr{H} \oplus l^2(\mathscr{D}_T)$, where  $\mathscr{D}_T=\overline{Ran}(I-T^*T)^{\frac{1}{2}}$ (see Theorem 3.5). We also show in Theorem 3.9 that such a dilation can be constructed with the conditions (1)–(4) of Theorem 1.1 only, though we do not have an exact converse part then. A special emphasis is given to the case when the product T is a
$\mathscr{D}_T=\overline{Ran}(I-T^*T)^{\frac{1}{2}}$ (see Theorem 3.5). We also show in Theorem 3.9 that such a dilation can be constructed with the conditions (1)–(4) of Theorem 1.1 only, though we do not have an exact converse part then. A special emphasis is given to the case when the product T is a ![]() $C._0$ contraction, i.e.,
$C._0$ contraction, i.e., ![]() ${T^*}^n\rightarrow 0$ strongly as
${T^*}^n\rightarrow 0$ strongly as ![]() $n\rightarrow \infty$. We show in Theorem 4.1 that an analogue of Theorem 1.1 can be achieved for the
$n\rightarrow \infty$. We show in Theorem 4.1 that an analogue of Theorem 1.1 can be achieved for the ![]() $C._0$ case with a weaker hypothesis. We explicitly construct an isometric dilation in this case too. This leads to a functional model and a factorization of a
$C._0$ case with a weaker hypothesis. We explicitly construct an isometric dilation in this case too. This leads to a functional model and a factorization of a ![]() $C._0$ contraction. A notable fact about this model is that the multipliers involved here are linear analytic functions in one variable. In Theorem 6.1, another main result of this article, we construct explicitly a similar isometric dilation for
$C._0$ contraction. A notable fact about this model is that the multipliers involved here are linear analytic functions in one variable. In Theorem 6.1, another main result of this article, we construct explicitly a similar isometric dilation for ![]() $(T_1, \dots, T_n)$ on the Sz. Nagy–Foias minimal isometric dilation space of T. In §5, we provide several examples describing different classes of commuting contractions that dilate to commuting isometries conditionally. There we show that our classes of commuting contractions admitting isometric dilations are not properly contained in any of the previously determined classes in the literature. Also, none of such classes from the literature is a proper subclass of our classes; however, there are intersections. Finally, we present a model theory for a class of commuting contractions in §7.
$(T_1, \dots, T_n)$ on the Sz. Nagy–Foias minimal isometric dilation space of T. In §5, we provide several examples describing different classes of commuting contractions that dilate to commuting isometries conditionally. There we show that our classes of commuting contractions admitting isometric dilations are not properly contained in any of the previously determined classes in the literature. Also, none of such classes from the literature is a proper subclass of our classes; however, there are intersections. Finally, we present a model theory for a class of commuting contractions in §7.
2. A brief history of dilation on the polydisc
An isometric dilation ![]() $(V_1, \dots, V_n)$ of
$(V_1, \dots, V_n)$ of ![]() $(T_1, \dots, T_n)$ naturally extends to a tuple of commuting unitaries
$(T_1, \dots, T_n)$ naturally extends to a tuple of commuting unitaries ![]() $(U_1, \dots, U_n)$, and consequently,
$(U_1, \dots, U_n)$, and consequently, ![]() $(U_1, \dots, U_n)$ becomes a unitary dilation of
$(U_1, \dots, U_n)$ becomes a unitary dilation of ![]() $(T_1, \dots, T_n)$. Since
$(T_1, \dots, T_n)$. Since ![]() $(U_1, \dots, U_n)$ is a tuple of commuting unitaries having its Taylor joint spectrum on the n-torus
$(U_1, \dots, U_n)$ is a tuple of commuting unitaries having its Taylor joint spectrum on the n-torus ![]() $\mathbb{T}^n$, which is the distinguished boundary of the closed polydisc
$\mathbb{T}^n$, which is the distinguished boundary of the closed polydisc ![]() $\overline{\mathbb{D}}^n$, following Arveson’s terminology (see [Reference Arveson7]), we say that
$\overline{\mathbb{D}}^n$, following Arveson’s terminology (see [Reference Arveson7]), we say that ![]() $\overline{\mathbb{D}}^n$ is a complete spectral set for
$\overline{\mathbb{D}}^n$ is a complete spectral set for ![]() $(T_1, \dots, T_n)$. So, it follows that
$(T_1, \dots, T_n)$. So, it follows that ![]() $\overline{\mathbb{D}}^n$ is a spectral set for
$\overline{\mathbb{D}}^n$ is a spectral set for ![]() $(T_1, \dots, T_n)$. Thus, the n-tuples of commuting contractions that dilate to commuting isometries or unitaries must have
$(T_1, \dots, T_n)$. Thus, the n-tuples of commuting contractions that dilate to commuting isometries or unitaries must have ![]() $\overline{\mathbb{D}}^n$ as a spectral set. In [Reference Halmos37], Halmos constructed a unitary U on a certain larger space for a contraction T acting on a Hilbert space
$\overline{\mathbb{D}}^n$ as a spectral set. In [Reference Halmos37], Halmos constructed a unitary U on a certain larger space for a contraction T acting on a Hilbert space ![]() $\mathscr{H}$ such that
$\mathscr{H}$ such that ![]() $T=P_{\mathscr{H}}U|_{\mathscr{H}}$, which is to say that T is a compression of a unitary U. Existence of an isometry satisfying such a compression relation was proved before it by Julia, e.g., see [Reference Julia41–Reference Julia43]. The unitary dilation of Halmos was missing the compression-vs-dilation frame for positive integral powers of U and T. Later, Sz. Nagy resolved this issue in [Reference Sz.-Nagy58] with an innovative idea, where he proved that there is a Hilbert space
$T=P_{\mathscr{H}}U|_{\mathscr{H}}$, which is to say that T is a compression of a unitary U. Existence of an isometry satisfying such a compression relation was proved before it by Julia, e.g., see [Reference Julia41–Reference Julia43]. The unitary dilation of Halmos was missing the compression-vs-dilation frame for positive integral powers of U and T. Later, Sz. Nagy resolved this issue in [Reference Sz.-Nagy58] with an innovative idea, where he proved that there is a Hilbert space ![]() $\mathscr{K}$ containing
$\mathscr{K}$ containing ![]() $\mathscr{H}$ and a unitary U on
$\mathscr{H}$ and a unitary U on ![]() $\mathscr{K}$ such that
$\mathscr{K}$ such that ![]() $T^n=P_{\mathscr{H}}U^n|_{\mathscr{H}}$ for any non-negative integer n. This is well-known as Sz. Nagy unitary dilation of a contraction. A few years after Sz. Nagy’s famous discovery, Douglas [Reference Douglas32] and Schäffer [Reference Shalit55] produced distinct and explicit constructions of such a unitary dilation (of a contraction). The pioneering works of Sz. Nagy, Douglas, and Schäffer were further generalized by Ando to a pair of commuting contractions. Indeed, in [Reference Ando4], Ando constructed an isometric dilation
$T^n=P_{\mathscr{H}}U^n|_{\mathscr{H}}$ for any non-negative integer n. This is well-known as Sz. Nagy unitary dilation of a contraction. A few years after Sz. Nagy’s famous discovery, Douglas [Reference Douglas32] and Schäffer [Reference Shalit55] produced distinct and explicit constructions of such a unitary dilation (of a contraction). The pioneering works of Sz. Nagy, Douglas, and Schäffer were further generalized by Ando to a pair of commuting contractions. Indeed, in [Reference Ando4], Ando constructed an isometric dilation ![]() $(V_1,V_2)$ for a pair of commuting contractions
$(V_1,V_2)$ for a pair of commuting contractions ![]() $(T_1,T_2)$. Success of dilation for a pair of commuting contractions led to the natural question, whether an arbitrary n-tuple of commuting contractions dilates to some n-tuple of commuting isometries or unitaries for
$(T_1,T_2)$. Success of dilation for a pair of commuting contractions led to the natural question, whether an arbitrary n-tuple of commuting contractions dilates to some n-tuple of commuting isometries or unitaries for ![]() $n\geq 3$. This question was answered negatively by Parrott in [Reference Parrott48] via a counter example. One way of realizing the impact of this dilation result is the celebrated von Neumann inequality.
$n\geq 3$. This question was answered negatively by Parrott in [Reference Parrott48] via a counter example. One way of realizing the impact of this dilation result is the celebrated von Neumann inequality.
Theorem 2.1 [Reference von Neumann62]
Let T be a contraction on some Hilbert space ![]() $\mathscr{H}$. Then, for every polynomial
$\mathscr{H}$. Then, for every polynomial ![]() $p\in \mathbb{C}[z]$,
$p\in \mathbb{C}[z]$,
 \begin{equation*} \|p(T\| \leq \sup_{|z|\leq 1}|p(z)|.\end{equation*}
\begin{equation*} \|p(T\| \leq \sup_{|z|\leq 1}|p(z)|.\end{equation*} It was observed that the existence of a unitary dilation is sufficient for a commuting tuple of contractions to satisfy von Neumann inequality. Using this principle, Crabb and Davie in [Reference Crabb and Davie26] and Varopoulos in [Reference Varopoulos60] produced examples of a triple of commuting contractions, which do not satisfy von Neumann inequality and hence do not admit a unitary dilation. These examples spurred a lot of mathematicians to look into the von Neumann inequality for commuting contractions at least on the finite dimensional spaces, [Reference Choi and Li25, Reference Drury33, Reference Drury34, Reference Holbrook40, Reference Knese44]. In their seminal article [Reference Agler and McCarthy3], Agler and McCarthy proved a sharper version of von Neumann inequality for a pair of commuting and strictly contractive matrices. In [Reference Das and Sarkar29], Das and Sarkar presented a new proof to the result of Agler and McCarthy with a refinement of the class of matrices. The impact of Ando’s dilation is eminent even in the 20th century. In [Reference Bagchi, Bhattacharyya and Misra12], Bagchi, Bhattacharyya, and Misra have presented an elementary proof of Ando’s theorem in a ![]() $C^*$-algebraic setting, within a restricted class of homomorphisms modelled after Parrott’s example. In [Reference Sau54], Sau gave new proofs to Ando’s dilation theorem with Schäffer- and Douglas-type constructions.
$C^*$-algebraic setting, within a restricted class of homomorphisms modelled after Parrott’s example. In [Reference Sau54], Sau gave new proofs to Ando’s dilation theorem with Schäffer- and Douglas-type constructions.
In [Reference Brehmer23], Brehmer introduced the concept of regular unitary dilation and systematically studied the existence of such dilation. For any ![]() $\alpha\in \mathbb{Z}^n$, let
$\alpha\in \mathbb{Z}^n$, let ![]() $ \alpha_{-}=(-\min\{o,\alpha_1\},\ldots, -\min\{0, \alpha_n\})$ and
$ \alpha_{-}=(-\min\{o,\alpha_1\},\ldots, -\min\{0, \alpha_n\})$ and ![]() $\alpha_{+}=(\max\{0,\alpha_1\},\ldots, \max\{0,\alpha_n\})$. For a given commuting n-tuple of contractions
$\alpha_{+}=(\max\{0,\alpha_1\},\ldots, \max\{0,\alpha_n\})$. For a given commuting n-tuple of contractions ![]() $(T_1,\ldots,T_n)$ and a tuple of positive integers
$(T_1,\ldots,T_n)$ and a tuple of positive integers ![]() $m=(m_1,\ldots,m_n)$, the following notation is used in the literature:
$m=(m_1,\ldots,m_n)$, the following notation is used in the literature: ![]() ${T}^m:=\Pi_{i=1}^nT_i^{m_i}$.
${T}^m:=\Pi_{i=1}^nT_i^{m_i}$.
Definition 2.2. § 9, [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]
A commuting n-tuple of unitaries ![]() $U=(U_1,\ldots,U_n)$ on a Hilbert space
$U=(U_1,\ldots,U_n)$ on a Hilbert space ![]() $\mathscr{K}$ is said to be a regular unitary dilation of a commuting n-tuple of contractions
$\mathscr{K}$ is said to be a regular unitary dilation of a commuting n-tuple of contractions ![]() $T=(T_1,\ldots,T_n)$ on
$T=(T_1,\ldots,T_n)$ on ![]() $\mathscr{H}\subseteq \mathscr{K}$, if, for any
$\mathscr{H}\subseteq \mathscr{K}$, if, for any ![]() $\alpha\in \mathbb{Z}^n$,
$\alpha\in \mathbb{Z}^n$,
Brehmer proved in [Reference Brehmer23] that a tuple of commuting contractions, if admits a regular unitary (or isometric) dilation, can be completely characterized by some positivity conditions, which is known as Brehmer’s positivity. A tuple T is said to satisfy Brehmer’s positivity condition if
 \begin{equation}
\sum_{F\subseteq G}(-1)^{|F|}T_{F}^*T_F\geq 0
\end{equation}
\begin{equation}
\sum_{F\subseteq G}(-1)^{|F|}T_{F}^*T_F\geq 0
\end{equation} for all ![]() $G\subseteq\{1,\ldots n \}$. It follows from the definition that the existence of a regular unitary dilation implies the existence of a unitary dilation for a commuting tuple of contractions. The study of Brehmer was further continued by Halperin in [Reference Halperin38] and [Reference Halperin39]. The positivity condition introduced by Brehmer attracted considerable attention, e.g., see the novel works due to Agler [Reference Agler1] and Curto and Vasilescu [Reference Curto and Vasilescu27],[Reference Curto and Vasilescu28]. Indeed, Curto and Vasilescu generalized the original theorem of Brehmer together with Agler’s results on hypercontractivity by general model theory for multi-operators which satisfy certain positivity conditions. An alternative approach to the results due to Agler, Curto, and Vasilescu was provided by Timotin in [Reference Timotin59]. Timotin’s approach had thrown some new light on the geometric and combinatorial parts of the model theory of Agler, Curto, and Vasilescu. In [Reference Binding, Farenick and Li22], Binding, Farenick, and Li proved that for every m-tuple of operators on a Hilbert space, one can simultaneously dilate them to normal operators on the same Hilbert space such that the dilating operators have finite spectrums. On the other hand, there are non-trivial results on dilation of contractive but not necessarily commuting tuples. In [Reference Davis30], Davis started studying such tuples, and then, Bunce [Reference Bunce24] and Frazho [Reference Frazho35] provided a wider and concrete form to this analysis. An extensive research in the direction of non-commuting dilation has been carried out by Popescu in [Reference Popescu49–Reference Popescu53] and also in collaboration with Arias in [Reference Arias and Popescu5, Reference Arias and Popescu6]. In [Reference Bhat, Bhattacharyya and Dey19], Bhat, Bhattacharyya, and Dey proved that for a commuting contractive tuple, the standard commuting dilation is the maximal commuting dilation sitting inside the standard non-commuting dilation.
$G\subseteq\{1,\ldots n \}$. It follows from the definition that the existence of a regular unitary dilation implies the existence of a unitary dilation for a commuting tuple of contractions. The study of Brehmer was further continued by Halperin in [Reference Halperin38] and [Reference Halperin39]. The positivity condition introduced by Brehmer attracted considerable attention, e.g., see the novel works due to Agler [Reference Agler1] and Curto and Vasilescu [Reference Curto and Vasilescu27],[Reference Curto and Vasilescu28]. Indeed, Curto and Vasilescu generalized the original theorem of Brehmer together with Agler’s results on hypercontractivity by general model theory for multi-operators which satisfy certain positivity conditions. An alternative approach to the results due to Agler, Curto, and Vasilescu was provided by Timotin in [Reference Timotin59]. Timotin’s approach had thrown some new light on the geometric and combinatorial parts of the model theory of Agler, Curto, and Vasilescu. In [Reference Binding, Farenick and Li22], Binding, Farenick, and Li proved that for every m-tuple of operators on a Hilbert space, one can simultaneously dilate them to normal operators on the same Hilbert space such that the dilating operators have finite spectrums. On the other hand, there are non-trivial results on dilation of contractive but not necessarily commuting tuples. In [Reference Davis30], Davis started studying such tuples, and then, Bunce [Reference Bunce24] and Frazho [Reference Frazho35] provided a wider and concrete form to this analysis. An extensive research in the direction of non-commuting dilation has been carried out by Popescu in [Reference Popescu49–Reference Popescu53] and also in collaboration with Arias in [Reference Arias and Popescu5, Reference Arias and Popescu6]. In [Reference Bhat, Bhattacharyya and Dey19], Bhat, Bhattacharyya, and Dey proved that for a commuting contractive tuple, the standard commuting dilation is the maximal commuting dilation sitting inside the standard non-commuting dilation.
In [Reference Arveson8], Arveson considered a ![]() $d-$tuple
$d-$tuple ![]() $(T_1,\ldots,T_d)$ of mutually commuting operators acting on a Hilbert space
$(T_1,\ldots,T_d)$ of mutually commuting operators acting on a Hilbert space ![]() $\mathscr{H}$ such that
$\mathscr{H}$ such that
He showed many of the operator-theoretic aspects of function theory of the unit disk generalize to that of the unit ball Bd in complex ![]() $d-$space, including von Neumann inequality and the model theory of contractions. Apart from this, the notable works due to Athavale [Reference Athavale9–Reference Athavale11], Druy [Reference Drury33], and Vasilescu [Reference Vasilescu61] were among the early contributors to the multi-parameter operator theory on the unit ball in
$d-$space, including von Neumann inequality and the model theory of contractions. Apart from this, the notable works due to Athavale [Reference Athavale9–Reference Athavale11], Druy [Reference Drury33], and Vasilescu [Reference Vasilescu61] were among the early contributors to the multi-parameter operator theory on the unit ball in ![]() $\mathbb{C}^n$. In [Reference Müller and Vasilescu46], Muller and Vasilescu analysed some positivity conditions for commuting multi-operators, which ensured the unitary equivalence of these objects to some standard models consisting of backwards multi-shifts. They considered spherical dilation of a tuple of commuting contractions
$\mathbb{C}^n$. In [Reference Müller and Vasilescu46], Muller and Vasilescu analysed some positivity conditions for commuting multi-operators, which ensured the unitary equivalence of these objects to some standard models consisting of backwards multi-shifts. They considered spherical dilation of a tuple of commuting contractions ![]() $(T_1,\ldots T_d)$ on
$(T_1,\ldots T_d)$ on ![]() $\mathscr{H}$. Such a tuple dilates to a tuple of commuting normal operators
$\mathscr{H}$. Such a tuple dilates to a tuple of commuting normal operators ![]() $(N_1,\ldots,N_d)$ on
$(N_1,\ldots,N_d)$ on ![]() $\mathscr{K} \supseteq \mathscr{H}$ satisfying
$\mathscr{K} \supseteq \mathscr{H}$ satisfying
In [Reference Müller and Vasilescu46], Muller and Vasilescu gave a necessary and sufficient condition for a commuting multi-operator to have spherical dilation in terms of positivity of certain operator polynomials involving T and ![]() $T^*$. The dilation results of Sz. Nagy [Reference Sz.-Nagy57] for contractions and Agler [Reference Agler2] for
$T^*$. The dilation results of Sz. Nagy [Reference Sz.-Nagy57] for contractions and Agler [Reference Agler2] for ![]() $m-$hypercontractions follow as a special case of the result due to Muller and Vasilescu. It is evident that, unlike unitary dilation, the tuple of contractions that admit regular dilations can be completely characterized by Brehmer’s positivity conditions [Reference Brehmer23]. So, this means that Curto and Vasilescu in [Reference Curto and Vasilescu28] have found a bigger class of contractive tuples, which admit commuting unitary dilations. Later Grinshpan, Kaliuzhnyi, Verbovetskyi, Vinnikov, and Woerdeman [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] extended this result to a bigger class, which was denoted by
$m-$hypercontractions follow as a special case of the result due to Muller and Vasilescu. It is evident that, unlike unitary dilation, the tuple of contractions that admit regular dilations can be completely characterized by Brehmer’s positivity conditions [Reference Brehmer23]. So, this means that Curto and Vasilescu in [Reference Curto and Vasilescu28] have found a bigger class of contractive tuples, which admit commuting unitary dilations. Later Grinshpan, Kaliuzhnyi, Verbovetskyi, Vinnikov, and Woerdeman [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] extended this result to a bigger class, which was denoted by  $\mathscr{P}^d_{p,q}$. Recently, Barik, Das, Haria, and Sarkar [Reference Barik, Das, Haria and Sarkar15] introduced even a larger class of commuting contractions, denoted by
$\mathscr{P}^d_{p,q}$. Recently, Barik, Das, Haria, and Sarkar [Reference Barik, Das, Haria and Sarkar15] introduced even a larger class of commuting contractions, denoted by ![]() $\mathscr{T}^n_{p,q}(\mathscr{H})$, which dilate to commuting isometries. Also, Barik and Das established a von Neumann inequality for a tuple of commuting contractions belonging to
$\mathscr{T}^n_{p,q}(\mathscr{H})$, which dilate to commuting isometries. Also, Barik and Das established a von Neumann inequality for a tuple of commuting contractions belonging to ![]() $\mathscr{B}^n_{p,q}$. In the expository essay [Reference Levy and Moshe Shalit45], Levy and Shalit discussed a finite dimensional approach to dilation theory and have answered to some extent how much of the dilation theory can work out within the realm of linear algebra. Also, an interested reader is referred to [Reference McCarthy and Shalit47] due to McCarthy and Shalit. In [Reference Stochel and Szafraniec56], Stochel and Szafraniec proposed a test for a commutative family of operators to have a unitary power dilation. For a detailed study of dilation theory, an interested reader is also referred to the nice survey articles by Bhattacharyya [Reference Bhattacharyya20] and Shalit [Reference Shalit55].
$\mathscr{B}^n_{p,q}$. In the expository essay [Reference Levy and Moshe Shalit45], Levy and Shalit discussed a finite dimensional approach to dilation theory and have answered to some extent how much of the dilation theory can work out within the realm of linear algebra. Also, an interested reader is referred to [Reference McCarthy and Shalit47] due to McCarthy and Shalit. In [Reference Stochel and Szafraniec56], Stochel and Szafraniec proposed a test for a commutative family of operators to have a unitary power dilation. For a detailed study of dilation theory, an interested reader is also referred to the nice survey articles by Bhattacharyya [Reference Bhattacharyya20] and Shalit [Reference Shalit55].
3. Schäffer-type minimal isometric dilation
Let us recall a few notations and terminologies from the literature. For a contraction T on a Hilbert space ![]() $\mathscr{H}$, the defect operator of T is the unique positive square root of
$\mathscr{H}$, the defect operator of T is the unique positive square root of ![]() $I-T^*T$, and it is denoted by DT. Also, the closure of the range of DT is denoted by
$I-T^*T$, and it is denoted by DT. Also, the closure of the range of DT is denoted by ![]() $\mathscr{D}_T$, i.e.,
$\mathscr{D}_T$, i.e., ![]() $\mathscr{D}_T=\overline{Ran} \, D_T$. A contraction
$\mathscr{D}_T=\overline{Ran} \, D_T$. A contraction ![]() $T\in \mathscr{B}(\mathscr{H})$ is called completely non-unitary or simply c.n.u. if there is no non-zero subspace
$T\in \mathscr{B}(\mathscr{H})$ is called completely non-unitary or simply c.n.u. if there is no non-zero subspace ![]() $\mathscr{H}_1$ of
$\mathscr{H}_1$ of ![]() $\mathscr{H}$ that reduces T and on which T acts as a unitary. The classical L 2 space consists of complex-valued functions defined on the unit circle
$\mathscr{H}$ that reduces T and on which T acts as a unitary. The classical L 2 space consists of complex-valued functions defined on the unit circle ![]() $\mathbb{T}$ that are square integrable with respect to the Lebesgue measure on
$\mathbb{T}$ that are square integrable with respect to the Lebesgue measure on ![]() $\mathbb{T}$. A canonical basis for L 2 is
$\mathbb{T}$. A canonical basis for L 2 is ![]() $\{e^{in\theta}\,:\, n\in \mathbb Z \}$, and the closed subspace of L 2 generated by the basis
$\{e^{in\theta}\,:\, n\in \mathbb Z \}$, and the closed subspace of L 2 generated by the basis ![]() $\{e^{i n\theta}\,:\, n=0,1,2, \dots \}$ is denoted by
$\{e^{i n\theta}\,:\, n=0,1,2, \dots \}$ is denoted by ![]() $\widetilde{H}^2$. For any Hilbert space E, the space
$\widetilde{H}^2$. For any Hilbert space E, the space ![]() $L^2(E)$ is defined similarly as L 2, and the only difference is that the functions in
$L^2(E)$ is defined similarly as L 2, and the only difference is that the functions in ![]() $L^2(E)$ are E-valued. It is well-known that the Hilbert spaces
$L^2(E)$ are E-valued. It is well-known that the Hilbert spaces ![]() $L^2(E)$ and
$L^2(E)$ and ![]() $L^2 \otimes E$ are unitarily equivalent. Under this unitary equivalence, the replica of
$L^2 \otimes E$ are unitarily equivalent. Under this unitary equivalence, the replica of ![]() $\widetilde{H}^2 \otimes E$ in
$\widetilde{H}^2 \otimes E$ in ![]() $L^2(E)$ is denoted by
$L^2(E)$ is denoted by  $\widetilde{H}^2(E)$. A multiplication operator Mϕ on
$\widetilde{H}^2(E)$. A multiplication operator Mϕ on ![]() $L^2(E)$, where
$L^2(E)$, where ![]() $\phi(z)$ is an essentially bounded function from
$\phi(z)$ is an essentially bounded function from ![]() $\mathbb{T}$ to E, i.e.
$\mathbb{T}$ to E, i.e. ![]() $\phi \in L^{\infty}(E)$, is defined by
$\phi \in L^{\infty}(E)$, is defined by ![]() $M_{\phi}f(z)=\phi(z)f(z)$. For any
$M_{\phi}f(z)=\phi(z)f(z)$. For any ![]() $\phi \in L^{\infty}(E)$, the Toeplitz operator Tϕ on
$\phi \in L^{\infty}(E)$, the Toeplitz operator Tϕ on  $\widetilde{H}^2(E)$ is defined by
$\widetilde{H}^2(E)$ is defined by ![]() $T_{\phi}f(z)=P \phi(z)f(z)$, where
$T_{\phi}f(z)=P \phi(z)f(z)$, where  $P:L^2(E) \rightarrow \widetilde{H}^2(E)$ is the orthogonal projection. For any Hilbert space E, the Hardy space
$P:L^2(E) \rightarrow \widetilde{H}^2(E)$ is the orthogonal projection. For any Hilbert space E, the Hardy space ![]() $H^2(E)$ consists of analytic functions from the unit disk
$H^2(E)$ consists of analytic functions from the unit disk ![]() $\mathbb{D}$ to E with square summable coefficients in its power series, i.e.,
$\mathbb{D}$ to E with square summable coefficients in its power series, i.e.,
 \begin{align*}
H^2(E)& =\left\{f:\mathbb{D} \rightarrow E \,:\, f(z)=\sum_{i=0}^{\infty} \, a_nz^n\,, \, \, a_n \in E \, \text{for all } n\in \mathbb N \cup \{0\} \right.\\
& \qquad \times \left. \sum_{i=0}^{\infty}\, \|a_n\|^2 \lt \infty \right\}.
\end{align*}
\begin{align*}
H^2(E)& =\left\{f:\mathbb{D} \rightarrow E \,:\, f(z)=\sum_{i=0}^{\infty} \, a_nz^n\,, \, \, a_n \in E \, \text{for all } n\in \mathbb N \cup \{0\} \right.\\
& \qquad \times \left. \sum_{i=0}^{\infty}\, \|a_n\|^2 \lt \infty \right\}.
\end{align*} The Hilbert spaces  $\widetilde{H}^2(E)$ and
$\widetilde{H}^2(E)$ and ![]() $H^2(E)$ are unitarily equivalent. A multiplication operator Mϕ on
$H^2(E)$ are unitarily equivalent. A multiplication operator Mϕ on ![]() $H^2(E)$, where
$H^2(E)$, where ![]() $\phi(z)$ is an analytic multiplier, is defined by
$\phi(z)$ is an analytic multiplier, is defined by ![]() $M_{\phi}f(z)=\phi(z)f(z)$.
$M_{\phi}f(z)=\phi(z)f(z)$.
To explain the results of this section, we begin with the Berger–Coburn–Lebow model (or, simply the BCL model) for commuting isometries, which will be used in sequel.
Theorem 3.1 Berger–Coburn–Lebow, [Reference Berger, Coburn and Lebow18]
Let ![]() $V_1, \dots, V_n$ be commuting isometries on
$V_1, \dots, V_n$ be commuting isometries on ![]() $\mathscr{H}$ such that
$\mathscr{H}$ such that ![]() $V=\prod_{i=1}^n V_i$ is a pure isometry. Then, there exist projections
$V=\prod_{i=1}^n V_i$ is a pure isometry. Then, there exist projections ![]() $P_1, \dots, P_n$ and unitaries
$P_1, \dots, P_n$ and unitaries ![]() $U_1, \dots, U_n$ in
$U_1, \dots, U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{V^*})$ such that
$\mathscr{B}(\mathscr{D}_{V^*})$ such that
 \begin{equation*}
(V_1, \dots, V_n , V) \equiv (T_{P_1^{\perp}U_1+ zP_1U_1 }, \dots, T_{P_n^{\perp}U_n+zP_nU_n }, T_z) \;\; \text{on } \; \; H^2(\mathscr{D}_{V^*}).
\end{equation*}
\begin{equation*}
(V_1, \dots, V_n , V) \equiv (T_{P_1^{\perp}U_1+ zP_1U_1 }, \dots, T_{P_n^{\perp}U_n+zP_nU_n }, T_z) \;\; \text{on } \; \; H^2(\mathscr{D}_{V^*}).
\end{equation*} Later, Bercovici, Douglas, and Foias found a refined operator model for commuting c.n.u. isometries in [Reference Bercovici, Douglas and Foias16]. They introduced the notion of model n-isometries. A model n-isometry is a tuple of commuting n-isometries ![]() $(V_1, \dots, V_n)$ such that each Vi is a multiplication operator of the form
$(V_1, \dots, V_n)$ such that each Vi is a multiplication operator of the form  $M_{U_iP_i^{\perp}+zU_iP_i}$ and
$M_{U_iP_i^{\perp}+zU_iP_i}$ and ![]() $\prod_{i=1}^n V_i=M_z$, where
$\prod_{i=1}^n V_i=M_z$, where ![]() $P_1, \dots, P_n$ are orthogonal projections and
$P_1, \dots, P_n$ are orthogonal projections and ![]() $U_1, \dots, U_n$ are unitaries acting on a Hilbert space
$U_1, \dots, U_n$ are unitaries acting on a Hilbert space ![]() $\mathscr{H}$. The following characterization theorem for model n-isometries is nothing but a variant of the model due to Bercovici, Douglas, and Foias and a proof follows from lemma 2.2 in [Reference Bercovici, Douglas and Foias16] and the discussion below it. This will be used in sequel.
$\mathscr{H}$. The following characterization theorem for model n-isometries is nothing but a variant of the model due to Bercovici, Douglas, and Foias and a proof follows from lemma 2.2 in [Reference Bercovici, Douglas and Foias16] and the discussion below it. This will be used in sequel.
Theorem 3.2 Bercovici, Douglas, and Foias, [Reference Bercovici, Douglas and Foias16]
Let ![]() $U_1,\ldots,U_n$ be unitaries on Hilbert space
$U_1,\ldots,U_n$ be unitaries on Hilbert space ![]() $\mathscr{H}$ and
$\mathscr{H}$ and ![]() $P_1,\ldots,P_n$ be orthogonal projections on
$P_1,\ldots,P_n$ be orthogonal projections on ![]() $\mathscr{H}$. For each
$\mathscr{H}$. For each ![]() $1\leq i \leq n$, let
$1\leq i \leq n$, let  $V_i=M_{U_iP_i^{\perp}+zU_iP_i}$. Then,
$V_i=M_{U_iP_i^{\perp}+zU_iP_i}$. Then, ![]() $(V_1,\ldots,V_n)$ defines a commuting n-tuple of isometries with
$(V_1,\ldots,V_n)$ defines a commuting n-tuple of isometries with ![]() $\Pi_{i=1}^nV_i=M_z$ if and only if the following conditions are satisfied:
$\Pi_{i=1}^nV_i=M_z$ if and only if the following conditions are satisfied:
(1)
 $U_iU_j=U_jU_i$ for all
$U_iU_j=U_jU_i$ for all  $1\leq i \lt j \leq n$,
$1\leq i \lt j \leq n$,(2)
 $U_1\ldots U_n=I_{\mathscr{H}}$,
$U_1\ldots U_n=I_{\mathscr{H}}$,(3)
 $P_j+U_j^*P_iU_j=P_i+U_i^*P_jU_i \leq I_{\mathscr{H}}$ for all i ≠ j and
$P_j+U_j^*P_iU_j=P_i+U_i^*P_jU_i \leq I_{\mathscr{H}}$ for all i ≠ j and(4)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{H}}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{H}}$.
The following result is a corollary of Theorem 3.2. In other words, this can be treated as a variant of Theorem 3.2. We state it here so that we can directly apply it later.
Theorem 3.3 Let ![]() $U_1,\ldots,U_n$ be unitaries on Hilbert space
$U_1,\ldots,U_n$ be unitaries on Hilbert space ![]() $\mathscr{H}$ and
$\mathscr{H}$ and ![]() $P_1,\ldots,P_n$ be orthogonal projections on
$P_1,\ldots,P_n$ be orthogonal projections on ![]() $\mathscr{H}$. For each
$\mathscr{H}$. For each ![]() $1\leq i \leq n$, let
$1\leq i \leq n$, let  $V_i=M_{P_i^{\perp}U_i^*+zP_iU_i^*}$. Then,
$V_i=M_{P_i^{\perp}U_i^*+zP_iU_i^*}$. Then, ![]() $(V_1,\ldots,V_n)$ defines a commuting n-tuple of isometries with
$(V_1,\ldots,V_n)$ defines a commuting n-tuple of isometries with ![]() $\Pi_{i=1}^nV_i=M_z$ if and only if the following conditions are satisfied:
$\Pi_{i=1}^nV_i=M_z$ if and only if the following conditions are satisfied:
(1)
 $U_iU_j=U_jU_i$ for all
$U_iU_j=U_jU_i$ for all  $1\leq i \lt j \leq n$,
$1\leq i \lt j \leq n$,(2)
 $U_1\ldots U_n=I_{\mathscr{H}}$,
$U_1\ldots U_n=I_{\mathscr{H}}$,(3)
 $P_j+U_j^*P_iU_j=P_i+U_i^*P_jU_i \leq I_{\mathscr{H}}$ for all i ≠ j, and
$P_j+U_j^*P_iU_j=P_i+U_i^*P_jU_i \leq I_{\mathscr{H}}$ for all i ≠ j, and(4)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{H}}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{H}}$.
Now we present a twisted version of lemma 2.2 in [Reference Bercovici, Douglas and Foias16]. This will be used in the proof of the main theorem. For the sake of completeness, we give a proof here, and it goes along with similar arguments as in the proof of lemma 2.2 in [Reference Bercovici, Douglas and Foias16].
Lemma 3.4. Consider unitary operators ![]() $U,U_1$, and U 2 and orthogonal projections
$U,U_1$, and U 2 and orthogonal projections ![]() $P,P_1$, and P 2 on Hilbert space
$P,P_1$, and P 2 on Hilbert space ![]() $\mathscr{H}$. If
$\mathscr{H}$. If ![]() $V_{U,P},V_{U_1,P_1}$ and
$V_{U,P},V_{U_1,P_1}$ and ![]() $V_{U_2,P_2}$ on
$V_{U_2,P_2}$ on ![]() $H^2(\mathscr{H})$ are defined as
$H^2(\mathscr{H})$ are defined as ![]() $V_{U,P}=M_{P^{\perp}U^*+zPU^*}$,
$V_{U,P}=M_{P^{\perp}U^*+zPU^*}$,  $V_{U_1,P_1}=M_{P_1^{\perp}U_1^*+zP_1U_1^*}$, and
$V_{U_1,P_1}=M_{P_1^{\perp}U_1^*+zP_1U_1^*}$, and  $V_{U_2,P_2}=M_{P_2^{\perp}U_2^*+zP_2U_2^*}$, then the following are equivalent:
$V_{U_2,P_2}=M_{P_2^{\perp}U_2^*+zP_2U_2^*}$, then the following are equivalent:
(i)
 $ V_{U,P}=V_{U_1,P_1}V_{U_2,P_2} $,
$ V_{U,P}=V_{U_1,P_1}V_{U_2,P_2} $,(ii)
 $U=U_2U_1 $ and
$U=U_2U_1 $ and  $P=P_1+U_1^*P_2U_1$.
$P=P_1+U_1^*P_2U_1$.
Proof. We prove only ![]() $(i)\implies (ii)$, the proof of
$(i)\implies (ii)$, the proof of ![]() $(ii) \implies (i)$ follows trivially. From (i), we have
$(ii) \implies (i)$ follows trivially. From (i), we have ![]() $ V_{U,P}=V_{U_1,P_1}V_{U_2,P_2} $, and thus,
$ V_{U,P}=V_{U_1,P_1}V_{U_2,P_2} $, and thus,
 \begin{align*}
&P^{\perp}U^*+zPU^*=(P_1^{\perp}U_1^*+zP_1U_1^*)(P_2^{\perp}U_2^*+zP_2U_2^*),\\
\text{i.e.,}\quad &P^{\perp}U^*+zPU^* =P_1^{\perp}U_1^*P_2^{\perp}U_2^*+z(P_1U_1^*P_2^{\perp}U_2^*+P_1^{\perp}U_1^*P_2U_2^*)+z^2P_1U_1^*P_2U_2^*.
\end{align*}
\begin{align*}
&P^{\perp}U^*+zPU^*=(P_1^{\perp}U_1^*+zP_1U_1^*)(P_2^{\perp}U_2^*+zP_2U_2^*),\\
\text{i.e.,}\quad &P^{\perp}U^*+zPU^* =P_1^{\perp}U_1^*P_2^{\perp}U_2^*+z(P_1U_1^*P_2^{\perp}U_2^*+P_1^{\perp}U_1^*P_2U_2^*)+z^2P_1U_1^*P_2U_2^*.
\end{align*}Hence, we have
(1)
 $P^{\perp}U^*=P_1^{\perp}U_1^*P_2^{\perp}U_2^*$;
$P^{\perp}U^*=P_1^{\perp}U_1^*P_2^{\perp}U_2^*$;(2)
 $PU^*=P_1U_1^*P_2^{\perp}U_2^*+P_1^{\perp}U_1^*P_2U_2^* $;
$PU^*=P_1U_1^*P_2^{\perp}U_2^*+P_1^{\perp}U_1^*P_2U_2^* $;(3)
 $P_1U_1^*P_2U_2^*=0$.
$P_1U_1^*P_2U_2^*=0$.
From (2) and (3), by substituting ![]() $P_i^{\perp}=I-P_i$, we obtain
$P_i^{\perp}=I-P_i$, we obtain
From (1) and (3), by substituting ![]() $P_i^{\perp}=I-P_i$, we obtain
$P_i^{\perp}=I-P_i$, we obtain
Hence, (3.1) and (3.2) give us ![]() $U=U_2U_1$. Again, multiplying (3.1) from right by
$U=U_2U_1$. Again, multiplying (3.1) from right by ![]() $U_2U_1$ and substituting
$U_2U_1$ and substituting ![]() $U=U_2U_1$, we obtain
$U=U_2U_1$, we obtain ![]() $P=P_1+U_1^*P_2U_1$. The proof is now complete.
$P=P_1+U_1^*P_2U_1$. The proof is now complete.
We now present a Schäffer-type minimal isometric dilation for a tuple of commuting contractions, and this is one of the main results of this article. However, the proof of this theorem is going to be lengthy, and so, we will split the proof into several parts. We request the readers to kindly bear with us for once.
Theorem 3.5 Let ![]() $T_1,\ldots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions and let
$T_1,\ldots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions and let ![]() $T={\prod_{i=1}^n T_i}$.
$T={\prod_{i=1}^n T_i}$.
(a) If
 $\mathscr{K}$ is the minimal isometric dilation space of T, then
$\mathscr{K}$ is the minimal isometric dilation space of T, then  $(T_1,\ldots,T_n)$ possesses an isometric dilation
$(T_1,\ldots,T_n)$ possesses an isometric dilation  $(V_1,\ldots,V_{n})$ on
$(V_1,\ldots,V_{n})$ on  $\mathscr{K}$ with
$\mathscr{K}$ with  $V=\Pi_{i=1}^nV_i$ being the minimal isometric dilation of T if and only if there are unique orthogonal projections
$V=\Pi_{i=1}^nV_i$ being the minimal isometric dilation of T if and only if there are unique orthogonal projections  $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries  $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in  $\mathscr{B}(\mathscr{D}_T)$ with
$\mathscr{B}(\mathscr{D}_T)$ with  $\prod_{i=1}^n U_i=I_{\mathscr{D}_{T}}$ such that the following conditions are satisfied for each
$\prod_{i=1}^n U_i=I_{\mathscr{D}_{T}}$ such that the following conditions are satisfied for each  $i=1, \dots, n$:
$i=1, \dots, n$:(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_TU_iP_iU_i^*D_T=D_{T_i}^2$,
$D_TU_iP_iU_i^*D_T=D_{T_i}^2$,(5)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
(b) Such an isometric dilation is minimal and unique in the sense that if
 $(W_1, \dots, W_n)$ on
$(W_1, \dots, W_n)$ on  $\mathscr{K}_1$ and
$\mathscr{K}_1$ and  $(Y_1, \dots, Y_n)$ on
$(Y_1, \dots, Y_n)$ on  $\mathscr{K}_2$ are two isometric dilations of
$\mathscr{K}_2$ are two isometric dilations of  $(T_1, \dots, T_n)$ such that
$(T_1, \dots, T_n)$ such that  $W=\prod_{i=1}^nW_i$ and
$W=\prod_{i=1}^nW_i$ and  $Y=\prod_{i=1}^nY_i$ are minimal isometric dilations of T on
$Y=\prod_{i=1}^nY_i$ are minimal isometric dilations of T on  $\mathscr{K}_1$ and
$\mathscr{K}_1$ and  $\mathscr{K}_2$, respectively, then there is a unitary
$\mathscr{K}_2$, respectively, then there is a unitary  $\widetilde{U}:\mathscr{K}_1 \rightarrow \mathscr{K}_2$ such that
$\widetilde{U}:\mathscr{K}_1 \rightarrow \mathscr{K}_2$ such that  $(W_1, \dots, W_n)=(\widetilde{U}^*Y_1\widetilde{U}, \dots, \widetilde{U}^*Y_n\widetilde{U})$.
$(W_1, \dots, W_n)=(\widetilde{U}^*Y_1\widetilde{U}, \dots, \widetilde{U}^*Y_n\widetilde{U})$.
Proof. (a). (The ![]() $\Leftarrow$ part). Suppose there are projections
$\Leftarrow$ part). Suppose there are projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_T)$ with
$\mathscr{B}(\mathscr{D}_T)$ with ![]() $\prod_{i=1}^n U_i=I$ satisfying the operator identities (1)–(5) for
$\prod_{i=1}^n U_i=I$ satisfying the operator identities (1)–(5) for ![]() $1\leq i \leq n$. We first show that conditions (1)–(4) guarantee the existence of an isometric dilation of
$1\leq i \leq n$. We first show that conditions (1)–(4) guarantee the existence of an isometric dilation of ![]() $(T_1, \dots, T_n)$. In fact, we shall construct a co-isometric extension of
$(T_1, \dots, T_n)$. In fact, we shall construct a co-isometric extension of ![]() $(T_1^*, \dots, T_n^*)$. It is well-known from Sz. Nagy–Foias theory (see [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]) that any two minimal isometric dilations of a contraction are unitarily equivalent. Thus, without loss of generality, we consider the Schäffer’s minimal isometric dilation space
$(T_1^*, \dots, T_n^*)$. It is well-known from Sz. Nagy–Foias theory (see [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]) that any two minimal isometric dilations of a contraction are unitarily equivalent. Thus, without loss of generality, we consider the Schäffer’s minimal isometric dilation space ![]() $\mathscr{K}_0$ of T, where
$\mathscr{K}_0$ of T, where ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T})=\mathscr{H} \oplus \mathscr{D}_T \oplus \mathscr{D}_T \oplus \ldots$ and construct an isometric dilation on
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T})=\mathscr{H} \oplus \mathscr{D}_T \oplus \mathscr{D}_T \oplus \ldots$ and construct an isometric dilation on ![]() $\mathscr{K}_0$ for
$\mathscr{K}_0$ for ![]() $(T_1, \dots, T_n)$. Define Vi on
$(T_1, \dots, T_n)$. Define Vi on ![]() $\mathscr{K}_0$ as follows:
$\mathscr{K}_0$ as follows:
 \begin{equation}
V_i=\begin{bmatrix}
T_i&0&0&0&\ldots \\
P_iU_i^*D_T&P_i^{\perp}U_i^*&0&0&\ldots \\
0&P_iU_i^*&P_i^{\perp}U_i^*&0&\ldots \\
0&0&P_iU_i^*&P_i^{\perp}U_i^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}, \qquad 1\leq i \leq n.
\end{equation}
\begin{equation}
V_i=\begin{bmatrix}
T_i&0&0&0&\ldots \\
P_iU_i^*D_T&P_i^{\perp}U_i^*&0&0&\ldots \\
0&P_iU_i^*&P_i^{\perp}U_i^*&0&\ldots \\
0&0&P_iU_i^*&P_i^{\perp}U_i^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}, \qquad 1\leq i \leq n.
\end{equation} It is evident from the block matrix form that ![]() $V_i^*|_{\mathscr{H}} =T_i^*$ for each
$V_i^*|_{\mathscr{H}} =T_i^*$ for each ![]() $i=1, \ldots, n$.
$i=1, \ldots, n$.
Step 1. First we prove that ![]() $(V_1,\ldots,V_n)$ is a commuting tuple. For each
$(V_1,\ldots,V_n)$ is a commuting tuple. For each ![]() $i,j$, we have that
$i,j$, we have that
 \begin{align*}
V_iV_j & =
\left[\begin{matrix}
T_iT_j&0\\
P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T & P_i^{\perp}U_i^*P_j^{\perp}U_j^* \\
P_iU_i^*P_jU_j^*D_T&P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*\\
0&P_iU_i^*P_jU_j^*\\
\ldots & \ldots \end{matrix}\right. \\
& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left.\begin{matrix}
0&\ldots\\
0&\ldots \\
P_i^{\perp}U_i^*P_{j}^{\perp}U_j^*&\ldots \\
P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*& \ldots \\
\ldots & \ddots
\end{matrix}\right]
\end{align*}
\begin{align*}
V_iV_j & =
\left[\begin{matrix}
T_iT_j&0\\
P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T & P_i^{\perp}U_i^*P_j^{\perp}U_j^* \\
P_iU_i^*P_jU_j^*D_T&P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*\\
0&P_iU_i^*P_jU_j^*\\
\ldots & \ldots \end{matrix}\right. \\
& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left.\begin{matrix}
0&\ldots\\
0&\ldots \\
P_i^{\perp}U_i^*P_{j}^{\perp}U_j^*&\ldots \\
P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*& \ldots \\
\ldots & \ddots
\end{matrix}\right]
\end{align*}and
 \begin{align*}
V_iV_j & =
\left[\begin{matrix}
T_iT_j&0\\
P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T & P_i^{\perp}U_i^*P_j^{\perp}U_j^* \\
P_iU_i^*P_jU_j^*D_T&P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*\\
0&P_iU_i^*P_jU_j^*\\
\ldots & \ldots \end{matrix}\right. \\
& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left.\begin{matrix}
0&\ldots\\
0&\ldots \\
P_i^{\perp}U_i^*P_{j}^{\perp}U_j^*&\ldots \\
P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*& \ldots \\
\ldots & \ddots
\end{matrix}\right].
\end{align*}
\begin{align*}
V_iV_j & =
\left[\begin{matrix}
T_iT_j&0\\
P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T & P_i^{\perp}U_i^*P_j^{\perp}U_j^* \\
P_iU_i^*P_jU_j^*D_T&P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*\\
0&P_iU_i^*P_jU_j^*\\
\ldots & \ldots \end{matrix}\right. \\
& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \left.\begin{matrix}
0&\ldots\\
0&\ldots \\
P_i^{\perp}U_i^*P_{j}^{\perp}U_j^*&\ldots \\
P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*& \ldots \\
\ldots & \ddots
\end{matrix}\right].
\end{align*} Using the commutativity of ![]() $T_i,T_j$ and
$T_i,T_j$ and ![]() $U_i,U_j$ and applying condition (3) of the theorem, we obtain by simplifying the condition (2), i.e.,
$U_i,U_j$ and applying condition (3) of the theorem, we obtain by simplifying the condition (2), i.e.,  $
P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^* $, that
$
P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^* $, that
Now we show that
 \begin{equation}
P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*=P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*
\end{equation}
\begin{equation}
P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*=P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*
\end{equation}and
 \begin{equation}
P_jU_j^*D_TT_i+P_j^{\perp}U_j^*P_iU_i^*D_T=P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T.
\end{equation}
\begin{equation}
P_jU_j^*D_TT_i+P_j^{\perp}U_j^*P_iU_i^*D_T=P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T.
\end{equation}For showing (3.5), we see that
 \begin{align*}
P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*
& = P_jU_j^*(U_i^*-P_iU_i^*)+(U_j^*-P_jU_j^*)P_iU_i^*\\
& = P_jU_j^*U_i^*-P_jU_j^*P_iU_i^*+U_j^*P_iU_i^*-P_jU_j^*P_iU_i^*\\
& = P_iU_i^*U_j^*-P_iU_i^*P_jU_j^*+U_i^*P_jU_j^*-P_iU_i^*P_jU_j^*\\
& = P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*.
\end{align*}
\begin{align*}
P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*
& = P_jU_j^*(U_i^*-P_iU_i^*)+(U_j^*-P_jU_j^*)P_iU_i^*\\
& = P_jU_j^*U_i^*-P_jU_j^*P_iU_i^*+U_j^*P_iU_i^*-P_jU_j^*P_iU_i^*\\
& = P_iU_i^*U_j^*-P_iU_i^*P_jU_j^*+U_i^*P_jU_j^*-P_iU_i^*P_jU_j^*\\
& = P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*.
\end{align*}Note that the second last equality follows from Eq. (3.4) and condition (3) of Theorem 3.5.
To prove (3.6), we use a few conditions of Theorem 3.5 here. We have
 \begin{align*}
& P_jU_j^*D_TT_i+P_j^{\perp}U_j^*P_iU_i^*D_T\\
& \quad = P_jU_j^*(P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT)+P_j^{\perp}U_j^*P_iU_i^*D_T \;\;\; [\text{by condition (1)}] \\
& \quad = (P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*)D_T+P_jU_j^*P_iU_i^*D_TT\\
& \quad = (P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*)D_T+P_iU_i^*P_jU_j^*D_TT \\
& \kern67mm [\text{by } (3.5)~\text{and condition}(3) ] \\
& \quad = P_iU_i^*(P_j^{\perp}U_j^*D_T+P_jU_j^*D_TT)+P_i^{\perp}U_i^*P_jU_j^*D_T\\
& \quad = P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T. \kern27mm [\text{by condition (1)}]
\end{align*}
\begin{align*}
& P_jU_j^*D_TT_i+P_j^{\perp}U_j^*P_iU_i^*D_T\\
& \quad = P_jU_j^*(P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT)+P_j^{\perp}U_j^*P_iU_i^*D_T \;\;\; [\text{by condition (1)}] \\
& \quad = (P_jU_j^*P_i^{\perp}U_i^*+P_j^{\perp}U_j^*P_iU_i^*)D_T+P_jU_j^*P_iU_i^*D_TT\\
& \quad = (P_iU_i^*P_j^{\perp}U_j^*+P_i^{\perp}U_i^*P_jU_j^*)D_T+P_iU_i^*P_jU_j^*D_TT \\
& \kern67mm [\text{by } (3.5)~\text{and condition}(3) ] \\
& \quad = P_iU_i^*(P_j^{\perp}U_j^*D_T+P_jU_j^*D_TT)+P_i^{\perp}U_i^*P_jU_j^*D_T\\
& \quad = P_iU_i^*D_TT_j+P_i^{\perp}U_i^*P_jU_j^*D_T. \kern27mm [\text{by condition (1)}]
\end{align*} Hence, it follows that ![]() $V_jV_i=V_iV_j$ for all
$V_jV_i=V_iV_j$ for all ![]() $ i,j $, and consequently,
$ i,j $, and consequently, ![]() $(V_1,\ldots,V_n)$ is a commuting tuple.
$(V_1,\ldots,V_n)$ is a commuting tuple.
Step 2. We now prove that each Vj is an isometry and that ![]() $(V_1, \dots, V_n)$ is an isometric dilation of
$(V_1, \dots, V_n)$ is an isometric dilation of ![]() $(T_1, \dots, T_n)$. Note that
$(T_1, \dots, T_n)$. Note that
 \begin{equation*}
V_j^*V_j= \begin{bmatrix}
T_j^*T_j+D_TU_jP_jU_j^*D_T&0&0&\ldots\\
U_jP_j^{\perp}P_jU_j^*D_T&U_jP_j^{\perp}U_j^*+U_jP_jU_j^*&U_jP_jP_j^{\perp}U_j &\ldots \\
0&U_jP_j^{\perp}P_jU_j^*&U_jP_j^{\perp}U_j^*+U_jP_jU_j^*&\ldots \\
0&0&U_jP_j^{\perp}P_jU_j^*& \ldots \\
\ldots&\ldots&\ldots &\ddots
\end{bmatrix}.
\end{equation*}
\begin{equation*}
V_j^*V_j= \begin{bmatrix}
T_j^*T_j+D_TU_jP_jU_j^*D_T&0&0&\ldots\\
U_jP_j^{\perp}P_jU_j^*D_T&U_jP_j^{\perp}U_j^*+U_jP_jU_j^*&U_jP_jP_j^{\perp}U_j &\ldots \\
0&U_jP_j^{\perp}P_jU_j^*&U_jP_j^{\perp}U_j^*+U_jP_jU_j^*&\ldots \\
0&0&U_jP_j^{\perp}P_jU_j^*& \ldots \\
\ldots&\ldots&\ldots &\ddots
\end{bmatrix}.
\end{equation*} By condition (4), we have ![]() $T_j^*T_j+D_TU_jP_jU_j^*D_T=I$. Also, the identities
$T_j^*T_j+D_TU_jP_jU_j^*D_T=I$. Also, the identities  $U_jP_j^{\perp}U_j^*+U_jP_jU_j^*=I$ and
$U_jP_j^{\perp}U_j^*+U_jP_jU_j^*=I$ and  $U_jP_jP_j^{\perp}U_j^*=U_jP_j^{\perp}P_jU_j^*=0$ follow trivially. Thus, we have that
$U_jP_jP_j^{\perp}U_j^*=U_jP_j^{\perp}P_jU_j^*=0$ follow trivially. Thus, we have that ![]() $V_j^*V_j=I$, and hence, Vj is an isometry for
$V_j^*V_j=I$, and hence, Vj is an isometry for ![]() $1\leq j \leq n$. It is evident from the block matrix of Vi that
$1\leq j \leq n$. It is evident from the block matrix of Vi that ![]() $V_i^*|_{\mathscr{H}}=T_i^*$ and thus
$V_i^*|_{\mathscr{H}}=T_i^*$ and thus ![]() $(V_1,\ldots,V_n)$ on
$(V_1,\ldots,V_n)$ on ![]() $\mathscr{K}_0$ is an isometric dilation of
$\mathscr{K}_0$ is an isometric dilation of ![]() $(T_1,\ldots,T_n)$.
$(T_1,\ldots,T_n)$.
Step 3. It remains to show that ![]() $\prod_{i=1}^nV_i=V$, where V on
$\prod_{i=1}^nV_i=V$, where V on ![]() $\mathscr{K}_0$ is the Schäffer’s minimal isometric dilation of T. Note that V has the block matrix
$\mathscr{K}_0$ is the Schäffer’s minimal isometric dilation of T. Note that V has the block matrix  $V=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}$ with respect to the decomposition
$V=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}$ with respect to the decomposition ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$, where
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$, where
 \begin{equation*}
C=\begin{bmatrix}
D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and } S=\begin{bmatrix}
0&0&0&\cdots\\
I&0&0&\cdots\\
0&I&0&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{equation*}
\begin{equation*}
C=\begin{bmatrix}
D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and } S=\begin{bmatrix}
0&0&0&\cdots\\
I&0&0&\cdots\\
0&I&0&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{equation*} Similarly, for all ![]() $1\leq i \leq n$, Vi has the following matrix form with respect to the decomposition
$1\leq i \leq n$, Vi has the following matrix form with respect to the decomposition ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$:
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$:
 \begin{equation*} V_i=\begin{bmatrix}
T_i&0\\
\widetilde{C}_i & \widetilde{S}_i
\end{bmatrix},
\end{equation*}
\begin{equation*} V_i=\begin{bmatrix}
T_i&0\\
\widetilde{C}_i & \widetilde{S}_i
\end{bmatrix},
\end{equation*}where
 \begin{align*}
\widetilde{C}_i& =\begin{bmatrix}
P_iU_i^*D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and }\\
\widetilde{S}_i& =\begin{bmatrix}
P_i^{\perp}U_i^*&0&0&\cdots\\
P_iU_i^*&P_i^{\perp}U_i^*&0&\cdots\\
0&P_iU_i^*&P_i^{\perp}U_i^*&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{align*}
\begin{align*}
\widetilde{C}_i& =\begin{bmatrix}
P_iU_i^*D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and }\\
\widetilde{S}_i& =\begin{bmatrix}
P_i^{\perp}U_i^*&0&0&\cdots\\
P_iU_i^*&P_i^{\perp}U_i^*&0&\cdots\\
0&P_iU_i^*&P_i^{\perp}U_i^*&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{align*} Up to a unitary ![]() $S\equiv M_z$ and
$S\equiv M_z$ and  $\widetilde{S}_i \equiv M_{P_i^{\perp}U_i^*+P_iU_i^*z}$ for
$\widetilde{S}_i \equiv M_{P_i^{\perp}U_i^*+P_iU_i^*z}$ for ![]() $1\leq i \leq n$ on
$1\leq i \leq n$ on ![]() $H^2(\mathscr{D}_T)$. Further (3.4) gives
$H^2(\mathscr{D}_T)$. Further (3.4) gives ![]() $P_i+U_i^*P_jU_j=P_j+U_j^*P_iU_j$. The conditions (1)–(4) of Theorem 3.3 follow from the hypotheses of this theorem. Therefore, we have
$P_i+U_i^*P_jU_j=P_j+U_j^*P_iU_j$. The conditions (1)–(4) of Theorem 3.3 follow from the hypotheses of this theorem. Therefore, we have  $\prod_{i=1}^n M_{P_i^{\perp}U_i^*+zP_iU_i^*}=M_z$ and consequently
$\prod_{i=1}^n M_{P_i^{\perp}U_i^*+zP_iU_i^*}=M_z$ and consequently  $S=\prod_{i=1}^n \widetilde{S}_i $. As observed by Bercovici, Douglas, and Foias in [Reference Bercovici, Douglas and Foias16], the terms involved in condition (5) are all mutually orthogonal projections. This is because the sum of projections Q 1 and Q 2 is again a projection if and only if they are mutually orthogonal. Now, suppose
$S=\prod_{i=1}^n \widetilde{S}_i $. As observed by Bercovici, Douglas, and Foias in [Reference Bercovici, Douglas and Foias16], the terms involved in condition (5) are all mutually orthogonal projections. This is because the sum of projections Q 1 and Q 2 is again a projection if and only if they are mutually orthogonal. Now, suppose
Then, clearly, each ![]() $\underline{U_k}$ is a unitary, and
$\underline{U_k}$ is a unitary, and ![]() $\underline{P_k}$ is a projection. Let us define
$\underline{P_k}$ is a projection. Let us define
 \begin{equation*}
V_{\underline{T_k},\underline{U_k},\underline{P_k}}=\begin{bmatrix}
\underline{T_k}&0&0&0&\ldots \\
\underline{P_k}\;\underline{U_k}^*D_T&\underline{P_k}^{\perp}\underline{U_k}^*&0&0&\ldots \\
0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&0&\ldots \\
0&0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}, \qquad 1\leq k \leq n.
\end{equation*}
\begin{equation*}
V_{\underline{T_k},\underline{U_k},\underline{P_k}}=\begin{bmatrix}
\underline{T_k}&0&0&0&\ldots \\
\underline{P_k}\;\underline{U_k}^*D_T&\underline{P_k}^{\perp}\underline{U_k}^*&0&0&\ldots \\
0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&0&\ldots \\
0&0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}, \qquad 1\leq k \leq n.
\end{equation*} We prove that  $V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$ for all
$V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$ for all ![]() $1\leq k \leq n-1$. Note that for all
$1\leq k \leq n-1$. Note that for all ![]() $1\leq k \leq n$,
$1\leq k \leq n$,  $V_{\underline{T_k},\underline{U_k},\underline{P_k}}$ has the following block matrix form with respect to the decomposition
$V_{\underline{T_k},\underline{U_k},\underline{P_k}}$ has the following block matrix form with respect to the decomposition ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$:
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_T)$:
 \begin{equation*} V_{\underline{T_k},\underline{U_k},\underline{P_k}}=\begin{bmatrix}
\underline{T_k}&0\\
\underline{C_k}&\underline{S_k}
\end{bmatrix}, \end{equation*}
\begin{equation*} V_{\underline{T_k},\underline{U_k},\underline{P_k}}=\begin{bmatrix}
\underline{T_k}&0\\
\underline{C_k}&\underline{S_k}
\end{bmatrix}, \end{equation*}where
 \begin{align*} \underline{C_k}& =\begin{bmatrix}
\underline{P_k}\;\underline{U_k}^*D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and }\\
\underline{S_k}& =\begin{bmatrix}
\underline{P_k}^{\perp}\underline{U_k}^*&0&0&\cdots\\
\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&0&\cdots\\
0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{align*}
\begin{align*} \underline{C_k}& =\begin{bmatrix}
\underline{P_k}\;\underline{U_k}^*D_T\\0\\0\\ \vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \ \text{and }\\
\underline{S_k}& =\begin{bmatrix}
\underline{P_k}^{\perp}\underline{U_k}^*&0&0&\cdots\\
\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&0&\cdots\\
0&\underline{P_k}\;\underline{U_k}^*&\underline{P_k}^{\perp}\underline{U_k}^*&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}:l^2(\mathscr{D}_T)\to l^2(\mathscr{D}_T).
\end{align*} It is clear from the definition that ![]() $\underline{U_{k+1}}=\underline{U_k}U_{k+1}$ and
$\underline{U_{k+1}}=\underline{U_k}U_{k+1}$ and ![]() $\underline{P_{k+1}}=\underline{P_k}+\underline{U_k}^*P_{k+1}\underline{U_k}$. Hence, Lemma 3.4 tells us that
$\underline{P_{k+1}}=\underline{P_k}+\underline{U_k}^*P_{k+1}\underline{U_k}$. Hence, Lemma 3.4 tells us that ![]() $\underline{S_{k+1}}=\underline{S_k}S_{k+1}$. From the construction, it is clear that
$\underline{S_{k+1}}=\underline{S_k}S_{k+1}$. From the construction, it is clear that ![]() $\underline{T_{k+1}}=\underline{T_k}T_{k+1}$. Hence, for proving
$\underline{T_{k+1}}=\underline{T_k}T_{k+1}$. Hence, for proving  $V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$, it suffices to prove
$V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$, it suffices to prove ![]() $\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}=\underline{C_{k+1}}$. Here,
$\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}=\underline{C_{k+1}}$. Here,
 \begin{equation*}\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}= \begin{bmatrix}
\underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\\ \underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\\0\\ \vdots
\end{bmatrix}. \end{equation*}
\begin{equation*}\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}= \begin{bmatrix}
\underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\\ \underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\\0\\ \vdots
\end{bmatrix}. \end{equation*} Note that ![]() $\underline{S_{k+1}}=\underline{S_k}S_{k+1}$ gives
$\underline{S_{k+1}}=\underline{S_k}S_{k+1}$ gives
 \begin{equation*}
\underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*=0 \quad \quad \underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*+\underline{P_k}\;\underline{U_k}^*P_{k+1}^{\perp}U_{k+1}^*=\underline{P_{k+1}}\;\underline{U^*_{k+1}}.
\end{equation*}
\begin{equation*}
\underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*=0 \quad \quad \underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*+\underline{P_k}\;\underline{U_k}^*P_{k+1}^{\perp}U_{k+1}^*=\underline{P_{k+1}}\;\underline{U^*_{k+1}}.
\end{equation*}Using these two equations and condition (1) of this theorem, we obtain the following:
 \begin{align}
& \underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\nonumber\\
& \quad =\underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T-\underline{P_k}\;\underline{U_k}^*P_{k+1}^{\perp}U_{k+1}^*D_T \nonumber \\
& \quad =\underline{P_k}\;\underline{U_k}^*(D_{T}T_{k+1}-P_{k+1}^{\perp}U_{k+1}^*D_T)+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T \nonumber \\
& \quad =\underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*D_TT+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T \nonumber \\
& \quad =\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T.
\end{align}
\begin{align}
& \underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_k}^{\perp}\underline{U_k}^*P_{k+1}U_{k+1}^*D_{T}\nonumber\\
& \quad =\underline{P_k}\;\underline{U_k}^*D_{T}T_{k+1}+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T-\underline{P_k}\;\underline{U_k}^*P_{k+1}^{\perp}U_{k+1}^*D_T \nonumber \\
& \quad =\underline{P_k}\;\underline{U_k}^*(D_{T}T_{k+1}-P_{k+1}^{\perp}U_{k+1}^*D_T)+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T \nonumber \\
& \quad =\underline{P_k}\;\underline{U_k}^*P_{k+1}U_{k+1}^*D_TT+\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T \nonumber \\
& \quad =\underline{P_{k+1}}\;\underline{U_{k+1}}^*D_T.
\end{align} This proves that ![]() $\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}=\underline{C_{k+1}}$, and hence,
$\underline{C_k}T_{k+1}+\underline{S_k}C_{k+1}=\underline{C_{k+1}}$, and hence,  $V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$ for all
$V_{\underline{T_k},\underline{U_k},\underline{P_k}}V_{T_{k+1},U_{k+1},P_{k+1}}=V_{\underline{T_{k+1}},\underline{U_{k+1}},\underline{P_{k+1}}}$ for all ![]() $1\leq k \leq n-1$. Therefore, by induction, we have that
$1\leq k \leq n-1$. Therefore, by induction, we have that ![]() $V_{\underline{T_n},\underline{U_n},\underline{P_n}}=V_1\ldots V_n $. Note that we have
$V_{\underline{T_n},\underline{U_n},\underline{P_n}}=V_1\ldots V_n $. Note that we have ![]() $ \underline{T_n}=T$,
$ \underline{T_n}=T$, ![]() $\underline{U_n}=U_1\ldots U_n=I $. Also, it follows from condition (5) that
$\underline{U_n}=U_1\ldots U_n=I $. Also, it follows from condition (5) that ![]() $\underline{P_n}=I $. Therefore,
$\underline{P_n}=I $. Therefore, ![]() $V_{\underline{T_n},\underline{U_n},\underline{P_n}}=V$, where V is the Schäffer’s minimal isometric dilation. Hence,
$V_{\underline{T_n},\underline{U_n},\underline{P_n}}=V$, where V is the Schäffer’s minimal isometric dilation. Hence, ![]() $\prod_{i=1}^n V_i=V$.
$\prod_{i=1}^n V_i=V$.
Step-4. We now show that such an isometric dilation ![]() $(V_1, \dots, V_n)$ is minimal. Note that
$(V_1, \dots, V_n)$ is minimal. Note that ![]() $V= \prod_{i=1}^n V_i$ is a minimal isometric dilation of
$V= \prod_{i=1}^n V_i$ is a minimal isometric dilation of ![]() $T= \prod_{i=1}^n T_i$. Therefore,
$T= \prod_{i=1}^n T_i$. Therefore,
Again
 \begin{equation*}
Span\, \{V_1^{k_1}\dots V_n^{k_n}h\,:\, h \in \mathscr{H} ,\, k_1,\dots, k_n \in \mathbb N \cup \{0 \}\, \} \subseteq \mathscr{K}.
\end{equation*}
\begin{equation*}
Span\, \{V_1^{k_1}\dots V_n^{k_n}h\,:\, h \in \mathscr{H} ,\, k_1,\dots, k_n \in \mathbb N \cup \{0 \}\, \} \subseteq \mathscr{K}.
\end{equation*}Therefore,
 \begin{align*}
\mathscr{K} & = \overline{Span}\, \{V_1^k\dots V_n^kh\,:\, h \in \mathscr{H} ,\, k \in \mathbb N \cup \{0 \}\, \} \\
& = \overline{Span}\, \{V_1^{k_1}\dots V_n^{k_n}h\,:\, h \in \mathscr{H} ,\, k_1,\dots, k_n \in \mathbb N \cup \{0 \}\, \},
\end{align*}
\begin{align*}
\mathscr{K} & = \overline{Span}\, \{V_1^k\dots V_n^kh\,:\, h \in \mathscr{H} ,\, k \in \mathbb N \cup \{0 \}\, \} \\
& = \overline{Span}\, \{V_1^{k_1}\dots V_n^{k_n}h\,:\, h \in \mathscr{H} ,\, k_1,\dots, k_n \in \mathbb N \cup \{0 \}\, \},
\end{align*} and consequently, ![]() $(V_1, \dots, V_n)$ is a minimal isometric dilation of
$(V_1, \dots, V_n)$ is a minimal isometric dilation of ![]() $(T_1, \dots, T_n)$.
$(T_1, \dots, T_n)$.
(The ![]() $\Rightarrow$ part). Let
$\Rightarrow$ part). Let ![]() $(W_1,\ldots,W_n)$ on
$(W_1,\ldots,W_n)$ on ![]() $\mathscr{K}$ be an isometric dilation of
$\mathscr{K}$ be an isometric dilation of ![]() $(T_1,\ldots,T_n)$ such that
$(T_1,\ldots,T_n)$ such that ![]() $W=\Pi_{i=1}^nW_i$ is the minimal isometric dilation of T. Then,
$W=\Pi_{i=1}^nW_i$ is the minimal isometric dilation of T. Then, ![]() $\mathscr{K}=\mathscr{H} \oplus \mathscr{H}^{\perp}$. Suppose
$\mathscr{K}=\mathscr{H} \oplus \mathscr{H}^{\perp}$. Suppose  $W_i'=\prod_{j \neq i}W_j$ for
$W_i'=\prod_{j \neq i}W_j$ for ![]() $1 \leq i \leq n$. So,
$1 \leq i \leq n$. So,
Since V on ![]() $\mathscr{K}_0=\mathscr{H} \oplus l^2(\mathscr{D}_T)$ is the minimal Schäffer’s isometric dilation of T, it follows that
$\mathscr{K}_0=\mathscr{H} \oplus l^2(\mathscr{D}_T)$ is the minimal Schäffer’s isometric dilation of T, it follows that
Therefore, the map ![]() $\tau: \mathscr{K}_0 \rightarrow \mathscr{K}$ defined by
$\tau: \mathscr{K}_0 \rightarrow \mathscr{K}$ defined by ![]() $\tau(V^nh)=W^nh$ is a unitary which is identity on
$\tau(V^nh)=W^nh$ is a unitary which is identity on ![]() $\mathscr{H}$. Thus,
$\mathscr{H}$. Thus, ![]() $\mathscr{H}$ is a reducing subspace for τ, and consequently,
$\mathscr{H}$ is a reducing subspace for τ, and consequently,  $\tau =\begin{pmatrix}
I & 0 \\
0 & \tau_1
\end{pmatrix}
$ for some unitary τ 1. Then,
$\tau =\begin{pmatrix}
I & 0 \\
0 & \tau_1
\end{pmatrix}
$ for some unitary τ 1. Then,  $W=\tau V \tau^* = \begin{bmatrix}
T & 0 \\
\tau_1C & \tau_1 S\tau_1^*
\end{bmatrix},
$ where
$W=\tau V \tau^* = \begin{bmatrix}
T & 0 \\
\tau_1C & \tau_1 S\tau_1^*
\end{bmatrix},
$ where  $V=\begin{bmatrix}
T & 0 \\
C & S
\end{bmatrix}
$ with
$V=\begin{bmatrix}
T & 0 \\
C & S
\end{bmatrix}
$ with
 \begin{equation*}
C=\begin{bmatrix}
D_T\\
0\\
0\\
\vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \quad \text{and } \quad S= \begin{bmatrix}
0&0&0&\cdots \\
I&0&0&\cdots\\
0&I&0&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}: l^2(\mathscr{D}_T) \to l^2(\mathscr{D}_T).
\end{equation*}
\begin{equation*}
C=\begin{bmatrix}
D_T\\
0\\
0\\
\vdots
\end{bmatrix}:\mathscr{H}\to l^2(\mathscr{D}_T) \quad \text{and } \quad S= \begin{bmatrix}
0&0&0&\cdots \\
I&0&0&\cdots\\
0&I&0&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}: l^2(\mathscr{D}_T) \to l^2(\mathscr{D}_T).
\end{equation*} Let us consider the commuting tuple of isometries  $(\widehat{V}_1, \dots, \widehat{V}_n)=(\tau^* W_1 \tau, \dots, \tau^* W_n \tau)$. Note that
$(\widehat{V}_1, \dots, \widehat{V}_n)=(\tau^* W_1 \tau, \dots, \tau^* W_n \tau)$. Note that  $\prod_{i=1}^n \widehat{V}_i= \tau^* W \tau = V$. Define
$\prod_{i=1}^n \widehat{V}_i= \tau^* W \tau = V$. Define  $\widehat{V}_i'=\prod_{j\neq i} \widehat{V}_j$ for
$\widehat{V}_i'=\prod_{j\neq i} \widehat{V}_j$ for ![]() $1 \leq i \leq n$. Evidently, each
$1 \leq i \leq n$. Evidently, each ![]() $\widehat{V}_i'$ is an isometry and
$\widehat{V}_i'$ is an isometry and  $\widehat{V}_i, \widehat{V}_j', V$ commute for all
$\widehat{V}_i, \widehat{V}_j', V$ commute for all ![]() $i,j$. Also,
$i,j$. Also,  $\widehat{V}_i=\widehat{V}_i^{\prime *}V$ for
$\widehat{V}_i=\widehat{V}_i^{\prime *}V$ for ![]() $i=1, \dots, n$. Suppose the block matrix of
$i=1, \dots, n$. Suppose the block matrix of ![]() $\widehat{V}_i$ with respect to the decomposition
$\widehat{V}_i$ with respect to the decomposition ![]() $\mathscr{H} \oplus l^2(\mathscr{D}_P)$ be
$\mathscr{H} \oplus l^2(\mathscr{D}_P)$ be  $\widehat{V}_i=\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix}$. Now by the commutativity of
$\widehat{V}_i=\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix}$. Now by the commutativity of ![]() $\widehat{V}_i$ and
$\widehat{V}_i$ and ![]() $\widehat{V}$, we have
$\widehat{V}$, we have
 \begin{align}
\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix}
\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}&=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}
\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix} \nonumber \\
i.e. \; \;
\begin{bmatrix}
T_iT+A_iC&A_iS\\
C_iT+S_iC&S_iS
\end{bmatrix}&=\begin{bmatrix}
TT_i&TA_i\\
CT_i+SC_i&CA_i+SS_i
\end{bmatrix}.
\end{align}
\begin{align}
\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix}
\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}&=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}
\begin{bmatrix}
T_i&A_i\\
C_i&S_i
\end{bmatrix} \nonumber \\
i.e. \; \;
\begin{bmatrix}
T_iT+A_iC&A_iS\\
C_iT+S_iC&S_iS
\end{bmatrix}&=\begin{bmatrix}
TT_i&TA_i\\
CT_i+SC_i&CA_i+SS_i
\end{bmatrix}.
\end{align} Since Ti and T commute, considering the ![]() $(1,1)$ position, we have
$(1,1)$ position, we have ![]() $A_iC=0$. We now show that
$A_iC=0$. We now show that ![]() $A_i=0$. Suppose
$A_i=0$. Suppose ![]() $A_i=(A_{i1},A_{i2}\ldots )$ on
$A_i=(A_{i1},A_{i2}\ldots )$ on ![]() $\mathscr{D}_T\oplus \mathscr{D}_T\oplus \ldots$. Then, the fact that
$\mathscr{D}_T\oplus \mathscr{D}_T\oplus \ldots$. Then, the fact that ![]() $A_iC=0$ implies
$A_iC=0$ implies ![]() $A_{i1}=0$ on
$A_{i1}=0$ on ![]() $\mathscr{D}_T$. Again
$\mathscr{D}_T$. Again ![]() $A_iS=TA_i$ gives
$A_iS=TA_i$ gives
 \begin{equation*}
\begin{bmatrix}
0&A_{i2}&A_{i3}&\cdots
\end{bmatrix} \begin{bmatrix}
0&0&\ldots \\
I&0&\ldots\\
0&I&\ldots\\
\vdots&\vdots&\ldots
\end{bmatrix}=\begin{bmatrix}
0&TA_{i2}&TA_{i3}&\cdots
\end{bmatrix},
\end{equation*}
\begin{equation*}
\begin{bmatrix}
0&A_{i2}&A_{i3}&\cdots
\end{bmatrix} \begin{bmatrix}
0&0&\ldots \\
I&0&\ldots\\
0&I&\ldots\\
\vdots&\vdots&\ldots
\end{bmatrix}=\begin{bmatrix}
0&TA_{i2}&TA_{i3}&\cdots
\end{bmatrix},
\end{equation*} which further implies that ![]() $A_{i2}=0$ and
$A_{i2}=0$ and ![]() $A_{ik}=TA_{i(k-1)}$ for all
$A_{ik}=TA_{i(k-1)}$ for all ![]() $k\geq 3$. Hence, inductively, we have
$k\geq 3$. Hence, inductively, we have ![]() $A_{ik}=0$. This proves that
$A_{ik}=0$. This proves that ![]() $A_i=0$. A similar argument holds if we consider the commutativity of
$A_i=0$. A similar argument holds if we consider the commutativity of ![]() $\widehat{V}_i'$ and V. Thus, with respect to the decomposition
$\widehat{V}_i'$ and V. Thus, with respect to the decomposition ![]() $\mathscr{K}=\mathscr{H}\oplus l^2(\mathscr{D}_T)$,
$\mathscr{K}=\mathscr{H}\oplus l^2(\mathscr{D}_T)$, ![]() $\widehat{V}_i$ and
$\widehat{V}_i$ and ![]() $\widehat{V}_i'$ have the following block matrix forms:
$\widehat{V}_i'$ have the following block matrix forms:
 \begin{equation}
\widehat{V}_i=
\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix} \,,\qquad
\widehat{V}_i'=
\begin{bmatrix}
T_i'&0\\
C_i'&S_i'
\end{bmatrix} \qquad \text{with} \quad T_i'={\prod_{i\neq j} T_j} \qquad (1 \leq i \leq n),
\end{equation}
\begin{equation}
\widehat{V}_i=
\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix} \,,\qquad
\widehat{V}_i'=
\begin{bmatrix}
T_i'&0\\
C_i'&S_i'
\end{bmatrix} \qquad \text{with} \quad T_i'={\prod_{i\neq j} T_j} \qquad (1 \leq i \leq n),
\end{equation} for some bounded operators ![]() $C_i, C_i'$ and
$C_i, C_i'$ and ![]() $S_i, S_i'$. It follows from the commutativity of
$S_i, S_i'$. It follows from the commutativity of  $\widehat{V}_i, \widehat{V}_i'$ with V that
$\widehat{V}_i, \widehat{V}_i'$ with V that ![]() $S_i,S_i'$ commute with S. Evidently,
$S_i,S_i'$ commute with S. Evidently, ![]() $S=M_z$ on
$S=M_z$ on ![]() $H^2(\mathscr{D}_T)$ and by being commutants of S,
$H^2(\mathscr{D}_T)$ and by being commutants of S, ![]() $S_i=M_{\phi}$ and
$S_i=M_{\phi}$ and  $S_i'=M_{\phi_i'}$ for some
$S_i'=M_{\phi_i'}$ for some ![]() $\phi_i, \phi_i' \in H^{\infty}(\mathscr{B}(\mathscr{D}_T))$. The relation
$\phi_i, \phi_i' \in H^{\infty}(\mathscr{B}(\mathscr{D}_T))$. The relation  $\widehat{V}_i=\widehat{V}_i^{\prime *}V$ gives
$\widehat{V}_i=\widehat{V}_i^{\prime *}V$ gives
 \begin{equation}
\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}=\begin{bmatrix}
T_i^{\prime *}&C_i^{\prime *}\\
0&S_i^{\prime *}
\end{bmatrix} \begin{bmatrix}
T&0\\
C&S
\end{bmatrix}= \begin{bmatrix}
T_i^{\prime *}T+C_i^{\prime *}C&C_i^{\prime *}S\\
S_i^{\prime *}C&S_i^{\prime *}S
\end{bmatrix},
\end{equation}
\begin{equation}
\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}=\begin{bmatrix}
T_i^{\prime *}&C_i^{\prime *}\\
0&S_i^{\prime *}
\end{bmatrix} \begin{bmatrix}
T&0\\
C&S
\end{bmatrix}= \begin{bmatrix}
T_i^{\prime *}T+C_i^{\prime *}C&C_i^{\prime *}S\\
S_i^{\prime *}C&S_i^{\prime *}S
\end{bmatrix},
\end{equation} where ![]() $T_i'$ is as in (3.9). Form here, we have the following identities for each
$T_i'$ is as in (3.9). Form here, we have the following identities for each ![]() $i=1, \dots, n$:
$i=1, \dots, n$:
(a)
 $T_i-T_i^{\prime *}T=C_i^{\prime *}C$,
$T_i-T_i^{\prime *}T=C_i^{\prime *}C$,(b)
 $C_i=(M_{\phi_i'})^*C$,
$C_i=(M_{\phi_i'})^*C$,(c)
 $M_{\phi_i}=(M_{\phi_i'})^*M_z. $
$M_{\phi_i}=(M_{\phi_i'})^*M_z. $
Again,  $\widehat{V}_i'=\widehat{V}_i^*V$ leads to
$\widehat{V}_i'=\widehat{V}_i^*V$ leads to
 \begin{equation}
\begin{bmatrix}
T_i'&0\\
C_i'&S_i'
\end{bmatrix}=\begin{bmatrix}
T_i^*&C_i^*\\
0&S_i^*
\end{bmatrix} \begin{bmatrix}
T&0\\
C&S
\end{bmatrix}= \begin{bmatrix}
T_i^*T+C_i^*C&C_i^*S\\
S_i^*C&S_i^*S
\end{bmatrix},
\end{equation}
\begin{equation}
\begin{bmatrix}
T_i'&0\\
C_i'&S_i'
\end{bmatrix}=\begin{bmatrix}
T_i^*&C_i^*\\
0&S_i^*
\end{bmatrix} \begin{bmatrix}
T&0\\
C&S
\end{bmatrix}= \begin{bmatrix}
T_i^*T+C_i^*C&C_i^*S\\
S_i^*C&S_i^*S
\end{bmatrix},
\end{equation} and hence, we have, for each ![]() $i=1, \dots, n$,
$i=1, \dots, n$,
(a’)
 $T_i'-T_i^*T=C_i^*C$,
$T_i'-T_i^*T=C_i^*C$,(b’)
 $C_i'=(M_{\phi_i})^*C$,
$C_i'=(M_{\phi_i})^*C$,(c’)
 $M_{\phi_i'}=(M_{\phi_i})^*M_z. $
$M_{\phi_i'}=(M_{\phi_i})^*M_z. $
From (c) above and considering the power series expansions of ϕi and ![]() $\phi_i'$, we have that
$\phi_i'$, we have that ![]() $\phi_i(z)=F_i+F_i^{\prime *}z$ and
$\phi_i(z)=F_i+F_i^{\prime *}z$ and ![]() $\phi_i'(z)=F_i'+F_i^*z$ for some
$\phi_i'(z)=F_i'+F_i^*z$ for some ![]() $F_i, F_i' \in \mathscr{B}(\mathscr{D}_T)$. Therefore,
$F_i, F_i' \in \mathscr{B}(\mathscr{D}_T)$. Therefore,
 \begin{equation*}
S_i=M_{\phi_i}=\begin{bmatrix}
F_i&0&0&\cdots \\
F_i^{\prime *}&F_i&0&\cdots\\
0&F_i^{\prime *}&F_i&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix} \;\; \text{and } \;\;
S_i'=M_{\phi_i'}=\begin{bmatrix}
F_i'&0&0&\cdots \\
F_i^*&F_i'&0&\cdots\\
0&F_i^*&F_i'&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}.
\end{equation*}
\begin{equation*}
S_i=M_{\phi_i}=\begin{bmatrix}
F_i&0&0&\cdots \\
F_i^{\prime *}&F_i&0&\cdots\\
0&F_i^{\prime *}&F_i&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix} \;\; \text{and } \;\;
S_i'=M_{\phi_i'}=\begin{bmatrix}
F_i'&0&0&\cdots \\
F_i^*&F_i'&0&\cdots\\
0&F_i^*&F_i'&\cdots\\
\vdots&\vdots&\vdots&\ddots
\end{bmatrix}.
\end{equation*} From (b) and ![]() $(b')$, we have that
$(b')$, we have that
 \begin{equation*}C_i=S_i^{\prime *}C=\begin{bmatrix}
F_i^{\prime *}D_T\\
0\\
0\\
\vdots
\end{bmatrix} \quad \text{and } \quad C_i'= S_i^*C=\begin{bmatrix}
F_i^*D_T\\
0\\
0\\
\vdots
\end{bmatrix}.
\end{equation*}
\begin{equation*}C_i=S_i^{\prime *}C=\begin{bmatrix}
F_i^{\prime *}D_T\\
0\\
0\\
\vdots
\end{bmatrix} \quad \text{and } \quad C_i'= S_i^*C=\begin{bmatrix}
F_i^*D_T\\
0\\
0\\
\vdots
\end{bmatrix}.
\end{equation*} The fact that ![]() $\widehat{V}_i$ and
$\widehat{V}_i$ and ![]() $\widehat{V}_i'$ are isometries gives us
$\widehat{V}_i'$ are isometries gives us ![]() $F_i'F_i=F_iF_i'=0$,
$F_i'F_i=F_iF_i'=0$, ![]() $F_i^*F_i+F_i'F_i^{\prime *}=F_i^{\prime *}F_i'+F_iF_i^*=I$ and
$F_i^*F_i+F_i'F_i^{\prime *}=F_i^{\prime *}F_i'+F_iF_i^*=I$ and  $D_TF_i'F_i^{\prime *}D_T=D_{T_i}^2$ for
$D_TF_i'F_i^{\prime *}D_T=D_{T_i}^2$ for ![]() $1\leq i \leq n$. Again, by the commutativity of
$1\leq i \leq n$. Again, by the commutativity of  $\widehat{V}_i, \widehat{V}_j$ and considering the
$\widehat{V}_i, \widehat{V}_j$ and considering the ![]() $(2,2)$ entries of their
$(2,2)$ entries of their ![]() $2 \times 2$ block-matrices, we have the commutativity of ϕi and ϕj. From here, we have
$2 \times 2$ block-matrices, we have the commutativity of ϕi and ϕj. From here, we have ![]() $[F_i,F_j]=0$ and
$[F_i,F_j]=0$ and ![]() $[F_i^*,F_j']=[F_j^*, F_i']$, and they hold for all
$[F_i^*,F_j']=[F_j^*, F_i']$, and they hold for all ![]() $1 \leq i,j \leq n$. Similarly, by the commutativity of
$1 \leq i,j \leq n$. Similarly, by the commutativity of  $\widehat{V}_i',\widehat{V}_j' $, we have that
$\widehat{V}_i',\widehat{V}_j' $, we have that ![]() $[F_i',F_j']=0$ for each
$[F_i',F_j']=0$ for each ![]() $i,j$. Thus, combining all together, we have the following identities for
$i,j$. Thus, combining all together, we have the following identities for ![]() $1\leq i,j \leq n$:
$1\leq i,j \leq n$:
 \begin{align}
&(i) \;\; F_iF_j = F_jF_i \;\; \;\; [F_i^*,F_j']=[F_j^*, F_i']
\end{align}
\begin{align}
&(i) \;\; F_iF_j = F_jF_i \;\; \;\; [F_i^*,F_j']=[F_j^*, F_i']
\end{align} \begin{align}
&(ii) \; \; F_i'F_j' =F_j'F_i'
\end{align}
\begin{align}
&(ii) \; \; F_i'F_j' =F_j'F_i'
\end{align} \begin{align}
& (v)\;\; D_TF_i'F_i^{\prime *}D_T=D_{T_i}^2.
\end{align}
\begin{align}
& (v)\;\; D_TF_i'F_i^{\prime *}D_T=D_{T_i}^2.
\end{align} For ![]() $1\leq i \leq n$, let us define
$1\leq i \leq n$, let us define  $
U_i=F_i^*+F_i',\;\; U_{i}'=F_i^*-F_i' , \;\; \text{and } \; \; P_i=\frac{1}{2}(I-U_{i}^{\prime *}U_{i}).
$ Applying the above identities involving Fi and
$
U_i=F_i^*+F_i',\;\; U_{i}'=F_i^*-F_i' , \;\; \text{and } \; \; P_i=\frac{1}{2}(I-U_{i}^{\prime *}U_{i}).
$ Applying the above identities involving Fi and ![]() $F_i'$, we have that
$F_i'$, we have that ![]() $U_i, U_i'$ are unitaries. Note that
$U_i, U_i'$ are unitaries. Note that ![]() $F_i=(U_i^*+U_i^{\prime *})/2$ and
$F_i=(U_i^*+U_i^{\prime *})/2$ and ![]() $F_i'=(U_i-U_i')/2$. Hence,
$F_i'=(U_i-U_i')/2$. Hence, ![]() $F_i'F_i=0$ implies that
$F_i'F_i=0$ implies that ![]() $U_iU_i^{\prime *}=U_i'U_i^*$, and
$U_iU_i^{\prime *}=U_i'U_i^*$, and ![]() $F_iF_i'=0$ implies that
$F_iF_i'=0$ implies that ![]() $U_i^*U_i'=U_i^{\prime *}U_i$. Thus,
$U_i^*U_i'=U_i^{\prime *}U_i$. Thus,  $P_i=\dfrac{1}{2}(I-U_i^*U_i')$. It follows from here that Pi is a projection. It can be verified that
$P_i=\dfrac{1}{2}(I-U_i^*U_i')$. It follows from here that Pi is a projection. It can be verified that ![]() $F_i'=U_iP_i$ and
$F_i'=U_iP_i$ and ![]() $F_i=P_i^{\perp}U_i^*.$ From (3.8), we have
$F_i=P_i^{\perp}U_i^*.$ From (3.8), we have ![]() $C_iT+S_iC=CT_i+SC_i$ for each i and substituting the values of
$C_iT+S_iC=CT_i+SC_i$ for each i and substituting the values of ![]() $C_i, S_i$ and C we have
$C_i, S_i$ and C we have
We now show that the unitaries ![]() $U_1, \dots, U_n$ commute. For each
$U_1, \dots, U_n$ commute. For each ![]() $i,j$ we have
$i,j$ we have
 \begin{align*}
U_iU_j= & (F_i^*+F_i')(F_j^*+F_j')\\
=&F_i^*F_j^*+(F_i^*F_j'+F_i'F_j^*)+F_i'F_j'\\
=&F_j^*F_i^*+(F_j^*F_i'+F_j'F_i^*)+F_j'F_i' \quad [\text{by the second part of } (3.12)]\\
=&U_jU_i.
\end{align*}
\begin{align*}
U_iU_j= & (F_i^*+F_i')(F_j^*+F_j')\\
=&F_i^*F_j^*+(F_i^*F_j'+F_i'F_j^*)+F_i'F_j'\\
=&F_j^*F_i^*+(F_j^*F_i'+F_j'F_i^*)+F_j'F_i' \quad [\text{by the second part of } (3.12)]\\
=&U_jU_i.
\end{align*} Thus, substituting ![]() $F_i'=U_iP_i$ and
$F_i'=U_iP_i$ and ![]() $F_i=P_i^{\perp}U_i^*$, we have from (3.17), (3.12)-part-1, (3.13), and (3.16)
$F_i=P_i^{\perp}U_i^*$, we have from (3.17), (3.12)-part-1, (3.13), and (3.16)
(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_TU_iP_iU_i^*D_T=D_{T_i}^2$,
$D_TU_iP_iU_i^*D_T=D_{T_i}^2$,
respectively, where ![]() $U_1, \dots, U_n \in \mathscr{B}(\mathscr{D}_T)$ are commuting unitaries and
$U_1, \dots, U_n \in \mathscr{B}(\mathscr{D}_T)$ are commuting unitaries and ![]() $P_1, \dots, P_n \in \mathscr{B}(\mathscr{D}_T)$ are orthogonal projections. Since
$P_1, \dots, P_n \in \mathscr{B}(\mathscr{D}_T)$ are orthogonal projections. Since  $\prod_{i=1}^n\widehat{V}_i=V$, the
$\prod_{i=1}^n\widehat{V}_i=V$, the ![]() $(2,2)$ entry of the block matrix gives
$(2,2)$ entry of the block matrix gives ![]() $\prod_{i=1}^nS_i=S$. Note that
$\prod_{i=1}^nS_i=S$. Note that ![]() $S_i=M_{\phi_i}$ for each i, where
$S_i=M_{\phi_i}$ for each i, where ![]() $\phi_i=F_i+zF_i^{\prime *} =P_i^{\perp}U_i^*+zP_iU_i^*$. So, we have
$\phi_i=F_i+zF_i^{\prime *} =P_i^{\perp}U_i^*+zP_iU_i^*$. So, we have  $\prod_{i=1}^nM_{P_i^{\perp}U_i^*+zP_iU_i^*}=M_z$. Thus, by Lemma 3.3,
$\prod_{i=1}^nM_{P_i^{\perp}U_i^*+zP_iU_i^*}=M_z$. Thus, by Lemma 3.3, ![]() $\prod_{i=1}^n U_i=I$ and (5) holds.
$\prod_{i=1}^n U_i=I$ and (5) holds.
Uniqueness. From (a) and ![]() $(a')$ we have
$(a')$ we have  $
D_{T_i'}^2T_i=D_TF_i'D_T$ and
$
D_{T_i'}^2T_i=D_TF_i'D_T$ and  $ D_{T_i}^2T_i'=D_TF_iD_T
$, respectively. If there is
$ D_{T_i}^2T_i'=D_TF_iD_T
$, respectively. If there is ![]() $G_i' \in \mathscr{B} ({\mathscr{D}_T})$ such that
$G_i' \in \mathscr{B} ({\mathscr{D}_T})$ such that  $D_{T_i'}^2T_i=D_TG_i'D_T$, then
$D_{T_i'}^2T_i=D_TG_i'D_T$, then ![]() $D_T(F_i'-G_i')D_T=0$, and thus, for any
$D_T(F_i'-G_i')D_T=0$, and thus, for any ![]() $h,g \in \mathscr{H}$, we have
$h,g \in \mathscr{H}$, we have
This shows that ![]() $F_i'=G_i'$ and hence
$F_i'=G_i'$ and hence ![]() $F_i'$ is unique. Similarly one can show that Fi is unique. Now
$F_i'$ is unique. Similarly one can show that Fi is unique. Now ![]() $F_i=P_i^{\perp}U_i$ and
$F_i=P_i^{\perp}U_i$ and ![]() $F_i'=U_iP_i$ and thus
$F_i'=U_iP_i$ and thus ![]() $U_i=F_i^*+F_i'$ and
$U_i=F_i^*+F_i'$ and ![]() $P_i=F_i^{\prime *}F_i'$. Evidently the uniqueness of
$P_i=F_i^{\prime *}F_i'$. Evidently the uniqueness of ![]() $F_i, F_i'$ gives the uniqueness of
$F_i, F_i'$ gives the uniqueness of ![]() $U_i, P_i$ for
$U_i, P_i$ for ![]() $1\leq i \leq n$.
$1\leq i \leq n$.
(b). The minimality of the dilation follows from the fact that ![]() $V=\prod_{i=1}^n V_i$ is the minimal isometric dilation of the product
$V=\prod_{i=1}^n V_i$ is the minimal isometric dilation of the product ![]() $T=\prod_{i=1}^n T_i$. Following the proof of the
$T=\prod_{i=1}^n T_i$. Following the proof of the ![]() $(\Rightarrow)$ part of
$(\Rightarrow)$ part of ![]() $\textbf{(a)}$ we see that any commuting isometric dilation
$\textbf{(a)}$ we see that any commuting isometric dilation ![]() $(W_1, \dots, W_n)$ of
$(W_1, \dots, W_n)$ of ![]() $(T_1, \dots, T_n)$ on a minimal isometric dilation space
$(T_1, \dots, T_n)$ on a minimal isometric dilation space ![]() $\mathscr{K}_1$ of T is unitarily equivalent to the isometric dilation
$\mathscr{K}_1$ of T is unitarily equivalent to the isometric dilation ![]() $(V_1, \dots, V_n)$ on the Schäffer’s minimal space
$(V_1, \dots, V_n)$ on the Schäffer’s minimal space ![]() $\mathscr{K}_0$. The rest of the argument follows and the proof is complete.
$\mathscr{K}_0$. The rest of the argument follows and the proof is complete.
Remark 3.6. Note that Theorem 3.5 actually provides a commutant lifting in several variables. In Theorem 3.5, the isometric dilation ![]() $(V_1, \dots, V_n)$ of a commuting contractive tuple
$(V_1, \dots, V_n)$ of a commuting contractive tuple ![]() $(T_1, \dots, T_n)$ is constructed in such a way that the product
$(T_1, \dots, T_n)$ is constructed in such a way that the product ![]() $V=\prod_{i=1}^n V_i$ becomes the minimal isometric dilation of the contraction
$V=\prod_{i=1}^n V_i$ becomes the minimal isometric dilation of the contraction ![]() $T=\prod_{i=1}^n T_i$. Also, it is evident from the block matrix form of Vi as in (3.3) that
$T=\prod_{i=1}^n T_i$. Also, it is evident from the block matrix form of Vi as in (3.3) that ![]() $\mathscr{H}$ is co-invariant under each Vi and
$\mathscr{H}$ is co-invariant under each Vi and ![]() $V_i^*|_{\mathscr{H}}=T_i^*$. Thus, each Ti is a commutant of T and is being lifted to Vi, which is a commutant of the minimal isometric dilation V of T.
$V_i^*|_{\mathscr{H}}=T_i^*$. Thus, each Ti is a commutant of T and is being lifted to Vi, which is a commutant of the minimal isometric dilation V of T.
Note 3.7.
Ando’s theorem tells us that every pair of commuting contractions ![]() $(T_1,T_2)$ dilates to a pair of commuting isometries
$(T_1,T_2)$ dilates to a pair of commuting isometries ![]() $(V_1,V_2)$, but
$(V_1,V_2)$, but ![]() $(T_1,T_2)$ may not have such an isometric dilation
$(T_1,T_2)$ may not have such an isometric dilation ![]() $(V_1,V_2)$ such that
$(V_1,V_2)$ such that ![]() $V=V_1V_2$ is the minimal isometric dilation of
$V=V_1V_2$ is the minimal isometric dilation of ![]() $T=T_1T_2$. The following example shows that there are commuting contractions
$T=T_1T_2$. The following example shows that there are commuting contractions ![]() $T_1,T_2$ that violate the conditions of Theorem 3.5.
$T_1,T_2$ that violate the conditions of Theorem 3.5.
Example 3.8. Let us consider the following contractions on ![]() $\mathbb C^3$:
$\mathbb C^3$:
 \begin{equation*}
T_1=\begin{pmatrix}
0&0&0\\
1/3&0&0\\
0&1/3\sqrt{3}&0
\end{pmatrix} \quad \quad
T_2=\begin{pmatrix}
0&0&0\\
0&0&0\\
-1/\sqrt{3}&0&0
\end{pmatrix}.
\end{equation*}
\begin{equation*}
T_1=\begin{pmatrix}
0&0&0\\
1/3&0&0\\
0&1/3\sqrt{3}&0
\end{pmatrix} \quad \quad
T_2=\begin{pmatrix}
0&0&0\\
0&0&0\\
-1/\sqrt{3}&0&0
\end{pmatrix}.
\end{equation*} Evidently, ![]() $T=T_1T_2=0$, and thus,
$T=T_1T_2=0$, and thus, ![]() $D_T=I$. We show that
$D_T=I$. We show that ![]() $(T_1, T_2)$ does not dilate to a commuting pair of isometries acting on the minimal dilation space of T. Suppose it happens. Then, there exist projections
$(T_1, T_2)$ does not dilate to a commuting pair of isometries acting on the minimal dilation space of T. Suppose it happens. Then, there exist projections ![]() $P_1,P_2$ and commuting unitaries
$P_1,P_2$ and commuting unitaries ![]() $U_1,U_2$ in
$U_1,U_2$ in ![]() $\mathscr{B}(\mathscr{D}_T)$ with
$\mathscr{B}(\mathscr{D}_T)$ with ![]() $U_1U_2=I$ satisfying conditions (1)–(5) of Theorem 3.5. Following the arguments in the
$U_1U_2=I$ satisfying conditions (1)–(5) of Theorem 3.5. Following the arguments in the ![]() $(\Rightarrow)$ part of the proof of Theorem 3.5, we see that
$(\Rightarrow)$ part of the proof of Theorem 3.5, we see that ![]() $T_1,T_2$ satisfy (a) for
$T_1,T_2$ satisfy (a) for ![]() $i=1,2$ (see the first display after (3.10)), i.e.,
$i=1,2$ (see the first display after (3.10)), i.e.,
Since ![]() $D_T=I$, we have that
$D_T=I$, we have that ![]() $U_1P_1=T_2$ and
$U_1P_1=T_2$ and ![]() $U_2P_2=T_1$. Now we have
$U_2P_2=T_1$. Now we have
 \begin{align*}
D_TU_1P_1U_1^*D_T& =U_1P_1U_1^*=T_2T_2^*\\
& =\begin{pmatrix}
0&0&0\\0&0&0\\-1/\sqrt{3}&0&0
\end{pmatrix}\begin{pmatrix}
0&0&-1/\sqrt{3}\\
0&0&0\\
0&0&0
\end{pmatrix}=\begin{pmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{pmatrix}.
\end{align*}
\begin{align*}
D_TU_1P_1U_1^*D_T& =U_1P_1U_1^*=T_2T_2^*\\
& =\begin{pmatrix}
0&0&0\\0&0&0\\-1/\sqrt{3}&0&0
\end{pmatrix}\begin{pmatrix}
0&0&-1/\sqrt{3}\\
0&0&0\\
0&0&0
\end{pmatrix}=\begin{pmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{pmatrix}.
\end{align*}Also,
 \begin{equation*}
D_{T_1}^2=I-T_1^*T_1=\begin{pmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{pmatrix}-\begin{pmatrix}
0&1/3&0\\
0&0&1/3\sqrt{3}\\
0&0&0
\end{pmatrix}\begin{pmatrix}
0&0&0\\
1/3&0&0\\
0&1/3\sqrt{3}&0
\end{pmatrix}.
\end{equation*}
\begin{equation*}
D_{T_1}^2=I-T_1^*T_1=\begin{pmatrix}
1&0&0\\
0&1&0\\
0&0&1
\end{pmatrix}-\begin{pmatrix}
0&1/3&0\\
0&0&1/3\sqrt{3}\\
0&0&0
\end{pmatrix}\begin{pmatrix}
0&0&0\\
1/3&0&0\\
0&1/3\sqrt{3}&0
\end{pmatrix}.
\end{equation*}Thus,
 \begin{equation*}
D_{T_1}^2=\begin{pmatrix}8/9&0&0\\0&26/27&0\\0&0&1 \end{pmatrix}.
\end{equation*}
\begin{equation*}
D_{T_1}^2=\begin{pmatrix}8/9&0&0\\0&26/27&0\\0&0&1 \end{pmatrix}.
\end{equation*} Hence,  $D_TU_1P_1U_1^*D_T\neq D_{T_1}^2$, which contradicts condition (4) of Theorem 3.5. Hence
$D_TU_1P_1U_1^*D_T\neq D_{T_1}^2$, which contradicts condition (4) of Theorem 3.5. Hence ![]() $(T_1,T_2)$ does not dilate to a pair of commuting isometries
$(T_1,T_2)$ does not dilate to a pair of commuting isometries ![]() $(V_1,V_2)$ acting on the minimal isometric dilation space of
$(V_1,V_2)$ acting on the minimal isometric dilation space of ![]() $T=T_1T_2$.
$T=T_1T_2$.
It is evident from the first part of the proof of Theorem 3.5 that such an isometric dilation ![]() $(V_1, \dots, V_n)$ can be constructed for
$(V_1, \dots, V_n)$ can be constructed for ![]() $(T_1,\dots, T_n)$ with the help of conditions (1)–(4) of Theorem 3.5 and without even assuming that
$(T_1,\dots, T_n)$ with the help of conditions (1)–(4) of Theorem 3.5 and without even assuming that ![]() $\prod_{i=1}^n U_i=I$. Condition (5) was to make the product
$\prod_{i=1}^n U_i=I$. Condition (5) was to make the product ![]() $\prod_{i=1}^n V_i$ the minimal isometric dilation of
$\prod_{i=1}^n V_i$ the minimal isometric dilation of ![]() $\prod_{i=1}^n T_i$. Thus, a different version of Theorem 3.5 can be presented based on a weaker hypothesis in the following way. Needless to mention that a proof to this follows naturally from the proof of Theorem 3.5.
$\prod_{i=1}^n T_i$. Thus, a different version of Theorem 3.5 can be presented based on a weaker hypothesis in the following way. Needless to mention that a proof to this follows naturally from the proof of Theorem 3.5.
Theorem 3.9 Let ![]() $T_1,\ldots, T_n \in \mathscr{B}(\mathscr{H})$ be commuting contractions and let
$T_1,\ldots, T_n \in \mathscr{B}(\mathscr{H})$ be commuting contractions and let ![]() $T=\prod_{i=1}^nT_i$. Then,
$T=\prod_{i=1}^nT_i$. Then, ![]() $(T_1,\ldots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space of T if there are projections
$(T_1,\ldots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space of T if there are projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_T)$ such that the following hold for
$\mathscr{B}(\mathscr{D}_T)$ such that the following hold for ![]() $i=1, \dots, n$:
$i=1, \dots, n$:
(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_TU_iP_iU_i^*D_T=D_{T_i}^2$.
$D_TU_iP_iU_i^*D_T=D_{T_i}^2$.
Conversely, if ![]() $(T_1,\ldots,T_n)$ possesses an isometric dilation
$(T_1,\ldots,T_n)$ possesses an isometric dilation  $(\widehat{V}_1,\ldots,\widehat{V}_{n})$ with
$(\widehat{V}_1,\ldots,\widehat{V}_{n})$ with ![]() $V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T, then there are unique projections
$V=\prod_{i=1}^nV_i$ being the minimal isometric dilation of T, then there are unique projections ![]() $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_T)$ satisfying the conditions (1)–(4) above.
$\mathscr{B}(\mathscr{D}_T)$ satisfying the conditions (1)–(4) above.
4. Minimal isometric dilation and functional model when the product is a  $C._0$ contraction
$C._0$ contraction
In this section, we consider a tuple of commuting contractions ![]() $(T_1, \dots, T_n)$ with the product
$(T_1, \dots, T_n)$ with the product ![]() $T=\prod_{i=1}^n T_i$ being a
$T=\prod_{i=1}^n T_i$ being a ![]() $C._0$ contraction, i.e.,
$C._0$ contraction, i.e., ![]() ${T^*}^n \rightarrow 0$ strongly as
${T^*}^n \rightarrow 0$ strongly as ![]() $n \rightarrow \infty$. Such a tuple dilates (on the minimal isometric dilation space of T) with a weaker hypothesis than that of Theorem 3.5 as the following theorem shows. This is another main result of this article.
$n \rightarrow \infty$. Such a tuple dilates (on the minimal isometric dilation space of T) with a weaker hypothesis than that of Theorem 3.5 as the following theorem shows. This is another main result of this article.
Theorem 4.1 Let ![]() $T_1,\ldots,T_n$ be commuting contractions on a Hilbert space
$T_1,\ldots,T_n$ be commuting contractions on a Hilbert space ![]() $\mathscr{H}$ such that their product
$\mathscr{H}$ such that their product ![]() $T=\prod_{i=1}^nT_i$ is a
$T=\prod_{i=1}^nT_i$ is a ![]() $C._0$ contraction. Then,
$C._0$ contraction. Then, ![]() $(T_1,\ldots,T_n)$ possesses an isometric dilation
$(T_1,\ldots,T_n)$ possesses an isometric dilation ![]() $(V_1,\ldots,V_n)$ with
$(V_1,\ldots,V_n)$ with ![]() $V=\prod_{i=1}^nV_i$ being a minimal isometric dilation of T if and only if there are unique orthogonal projections
$V=\prod_{i=1}^nV_i$ being a minimal isometric dilation of T if and only if there are unique orthogonal projections ![]() $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ with
$\mathscr{B}(\mathscr{D}_{T^*})$ with ![]() $\prod_{i=1}^n U_i=I$ such that the following conditions hold for
$\prod_{i=1}^n U_i=I$ such that the following conditions hold for ![]() $i=1, \dots, n$:
$i=1, \dots, n$:
(1)
 $D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,
$D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_{T^*}}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_{T^*}}$.
Proof. First, we assume that there exist orthogonal projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that
$\mathscr{B}(\mathscr{D}_{T^*})$ such that ![]() $\prod_{i=1}^nU_i=I$ and the above conditions (1)–(4) hold. Since T is a
$\prod_{i=1}^nU_i=I$ and the above conditions (1)–(4) hold. Since T is a ![]() $C._0$ contraction,
$C._0$ contraction, ![]() $H^2(\mathscr{D}_{T^*})$ is a minimal isometric dilation space for T. We first construct an isometric dilation
$H^2(\mathscr{D}_{T^*})$ is a minimal isometric dilation space for T. We first construct an isometric dilation ![]() $(V_1, \dots, V_n)$ for
$(V_1, \dots, V_n)$ for ![]() $(T_1, \dots, T_n)$ on the minimal isometric dilation space
$(T_1, \dots, T_n)$ on the minimal isometric dilation space ![]() $H^2(\mathscr{D}_{T^*})$ of T with the assumptions
$H^2(\mathscr{D}_{T^*})$ of T with the assumptions ![]() $(1)-(3)$ only. Condition (4) will imply that
$(1)-(3)$ only. Condition (4) will imply that ![]() $\prod_{i=1}^n V_i=V$, the minimal isometric dilation of T. Let us consider the following multiplication operators acting on
$\prod_{i=1}^n V_i=V$, the minimal isometric dilation of T. Let us consider the following multiplication operators acting on ![]() $H^2(\mathscr{D}_{T^*})$:
$H^2(\mathscr{D}_{T^*})$:
 \begin{equation*}
V_i=M_{U_iP_i^{\perp}+zU_iP_i} \qquad (1\leq i \leq n).
\end{equation*}
\begin{equation*}
V_i=M_{U_iP_i^{\perp}+zU_iP_i} \qquad (1\leq i \leq n).
\end{equation*}Since Ui is a unitary and Pi is a projection, it follows that
and thus, Vi is an isometry for each i. Now we show that ![]() $(V_1, \dots, V_n)$ is a commuting tuple. Note that for any
$(V_1, \dots, V_n)$ is a commuting tuple. Note that for any ![]() $1\leq i \lt j\leq n$,
$1\leq i \lt j\leq n$, ![]() $V_iV_j=V_jV_i$ if and only if
$V_iV_j=V_jV_i$ if and only if
 \begin{equation*}
(U_iP_i^{\perp}+zU_iP_i)(U_jP_j^{\perp}+zU_jP_j)=(U_jP_j^{\perp}+zU_jP_j)(U_iP_i^{\perp}+zU_iP_i),
\end{equation*}
\begin{equation*}
(U_iP_i^{\perp}+zU_iP_i)(U_jP_j^{\perp}+zU_jP_j)=(U_jP_j^{\perp}+zU_jP_j)(U_iP_i^{\perp}+zU_iP_i),
\end{equation*}which happens if and only if the given conditions (2) and (3) hold along with
 \begin{equation}
U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j=U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp},
\end{equation}
\begin{equation}
U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j=U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp},
\end{equation} which we prove now. From the given condition (2), we have  $[U_iP_i^{\perp},U_jP_j^{\perp}]=0$, and this implies that
$[U_iP_i^{\perp},U_jP_j^{\perp}]=0$, and this implies that
From here we have that
We now prove that
 \begin{equation}
(U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j)=(U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp}).
\end{equation}
\begin{equation}
(U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j)=(U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp}).
\end{equation}We have that
 \begin{align*}
&(U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j)-(U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp})\\
& \quad =U_iP_iU_jP_j^{\perp}-U_jP_j^{\perp}U_iP_i-U_jP_jU_iP_i^{\perp}+U_iP_i^{\perp}U_jP_j\\
& \quad = U_iP_iU_j-U_iP_iU_jP_j-U_jU_iP_i+U_jP_jU_iP_i-U_jP_jU_i\\
& \qquad +U_jP_jU_iP_i+U_iU_jP_j-U_iP_iU_jP_j\\
& \quad =U_iP_iU_j-U_jU_iP_i-U_jP_jU_i+U_iU_jP_j \\
& \quad =0.\; \qquad [\text{by } (4.2)]
\end{align*}
\begin{align*}
&(U_iP_iU_jP_j^{\perp}+U_iP_i^{\perp}U_jP_j)-(U_jP_j^{\perp}U_iP_i+U_jP_jU_iP_i^{\perp})\\
& \quad =U_iP_iU_jP_j^{\perp}-U_jP_j^{\perp}U_iP_i-U_jP_jU_iP_i^{\perp}+U_iP_i^{\perp}U_jP_j\\
& \quad = U_iP_iU_j-U_iP_iU_jP_j-U_jU_iP_i+U_jP_jU_iP_i-U_jP_jU_i\\
& \qquad +U_jP_jU_iP_i+U_iU_jP_j-U_iP_iU_jP_j\\
& \quad =U_iP_iU_j-U_jU_iP_i-U_jP_jU_i+U_iU_jP_j \\
& \quad =0.\; \qquad [\text{by } (4.2)]
\end{align*} Therefore, (4.1) is proved, and consequently, ![]() $(V_1, \dots, V_n)$ is a tuple of commuting isometries. We now embed
$(V_1, \dots, V_n)$ is a tuple of commuting isometries. We now embed ![]() $\mathscr{H}$ inside
$\mathscr{H}$ inside ![]() $H^2(\mathscr{D}_{T^*})$. Let us define
$H^2(\mathscr{D}_{T^*})$. Let us define ![]() $W:\mathscr{H}\to H^2(\mathscr{D}_{T^*})$ by
$W:\mathscr{H}\to H^2(\mathscr{D}_{T^*})$ by
 \begin{equation}
W(h)=\sum_{0}^{\infty}z^n D_{T^*}T^{*n}h .
\end{equation}
\begin{equation}
W(h)=\sum_{0}^{\infty}z^n D_{T^*}T^{*n}h .
\end{equation}It can be found in the literature (e.g., [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]) that the map W is an isometry. However, we include a proof here for the sake of completeness and for the convenience of a reader.
 \begin{align*}
\|Wh\|^2 =\|\sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h\|^2
&= \left\langle \sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h, \sum_{m=0}^{\infty}z^mD_{T^*}T^{*m}h \right\rangle\\
&= \sum_{m,n=0}^{\infty}\langle z^n,z^m\rangle \langle D_{T^*}T^{*n}h, D_{T^*}T^{*m}h \rangle\\
&= \sum _{n=0}^{\infty} \langle T^nD_{T^*}^2T^{*n}h,h \rangle\\
&= \sum_{n=0}^{\infty} \langle T^n(I-TT^*)T^{*n}h,h \rangle \\
&= \sum_{n=0}^{\infty} (\langle T^nT^{*n}h,h\rangle - \langle T^{n+1}T^{*(n+1)}h,h\rangle ) \\
&= \lim_{m\to \infty }\sum_{n=0}^{m}(\|T^{*n}h\|^2-\|T^{*n+1}h\|^2)\\
&= \|h\|^2 - \lim_{m\to \infty }\|T^{*m}h\|^2\\
&=\|h\|^2.
\end{align*}
\begin{align*}
\|Wh\|^2 =\|\sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h\|^2
&= \left\langle \sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h, \sum_{m=0}^{\infty}z^mD_{T^*}T^{*m}h \right\rangle\\
&= \sum_{m,n=0}^{\infty}\langle z^n,z^m\rangle \langle D_{T^*}T^{*n}h, D_{T^*}T^{*m}h \rangle\\
&= \sum _{n=0}^{\infty} \langle T^nD_{T^*}^2T^{*n}h,h \rangle\\
&= \sum_{n=0}^{\infty} \langle T^n(I-TT^*)T^{*n}h,h \rangle \\
&= \sum_{n=0}^{\infty} (\langle T^nT^{*n}h,h\rangle - \langle T^{n+1}T^{*(n+1)}h,h\rangle ) \\
&= \lim_{m\to \infty }\sum_{n=0}^{m}(\|T^{*n}h\|^2-\|T^{*n+1}h\|^2)\\
&= \|h\|^2 - \lim_{m\to \infty }\|T^{*m}h\|^2\\
&=\|h\|^2.
\end{align*} The second last equality follows from the fact that  ${\displaystyle \lim_{n\to \infty }\|T^{*n}h\|^2=0}$ as T is a
${\displaystyle \lim_{n\to \infty }\|T^{*n}h\|^2=0}$ as T is a ![]() $C._0$ contraction. Thus, W is an isometry. We now determine the adjoint of W. For any
$C._0$ contraction. Thus, W is an isometry. We now determine the adjoint of W. For any ![]() $n\geq 0$,
$n\geq 0$, ![]() $\xi \in \mathscr{D}_{T^*}$, we have
$\xi \in \mathscr{D}_{T^*}$, we have
 \begin{equation*}
\langle W^*(z^n\xi),h \rangle = \langle z^n\xi, \sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h \rangle = \langle \xi, D_{T^*}T^{*n}h \rangle = \langle T^nD_{T^{*}}\xi, h \rangle .
\end{equation*}
\begin{equation*}
\langle W^*(z^n\xi),h \rangle = \langle z^n\xi, \sum_{n=0}^{\infty}z^nD_{T^*}T^{*n}h \rangle = \langle \xi, D_{T^*}T^{*n}h \rangle = \langle T^nD_{T^{*}}\xi, h \rangle .
\end{equation*} Therefore, ![]() $W^*(z^n\xi)=T^nD_{T^*}\xi$. Now for any
$W^*(z^n\xi)=T^nD_{T^*}\xi$. Now for any ![]() $1\leq i \leq n$, for all
$1\leq i \leq n$, for all ![]() $k\in \mathbb{N}\cup \{0 \}$ and for each
$k\in \mathbb{N}\cup \{0 \}$ and for each ![]() $\xi \in \mathscr{D}_{T^*}$, we have
$\xi \in \mathscr{D}_{T^*}$, we have
 \begin{align*}
W^*V_i(z^k\xi)& = W^*M_{U_iP_i^{\perp}+zU_iP_i}(z^k\xi)\\
& = W^*(z^kU_iP_i^{\perp}\xi+z^{k+1}U_iP_i\xi) =T^kD_{T^*}U_iP_i^{\perp}\xi+T^{k+1}D_{T^*}U_iP_i\xi \\
&=T^k(D_{T^*}U_iP_i^{\perp}\xi+TD_{T^*}U_iP_i\xi)\\
&=T^k(T_iD_{T^*}\xi) \;\; [\text{by condition }(1)]\\
&=T_i(T^kD_{T^*}\xi)\\
&=T_iW^*(z^k\xi).
\end{align*}
\begin{align*}
W^*V_i(z^k\xi)& = W^*M_{U_iP_i^{\perp}+zU_iP_i}(z^k\xi)\\
& = W^*(z^kU_iP_i^{\perp}\xi+z^{k+1}U_iP_i\xi) =T^kD_{T^*}U_iP_i^{\perp}\xi+T^{k+1}D_{T^*}U_iP_i\xi \\
&=T^k(D_{T^*}U_iP_i^{\perp}\xi+TD_{T^*}U_iP_i\xi)\\
&=T^k(T_iD_{T^*}\xi) \;\; [\text{by condition }(1)]\\
&=T_i(T^kD_{T^*}\xi)\\
&=T_iW^*(z^k\xi).
\end{align*} Therefore, ![]() $W^*V_i=T_iW^*$, i.e.,
$W^*V_i=T_iW^*$, i.e., ![]() $V_i^*W=WT_i^*=WT_i^*W^*W$, and hence,
$V_i^*W=WT_i^*=WT_i^*W^*W$, and hence, ![]() $V_i^*|_{W(\mathscr{H})}=WT_i^*W^*|_{W(\mathscr{H})}$. This proves that
$V_i^*|_{W(\mathscr{H})}=WT_i^*W^*|_{W(\mathscr{H})}$. This proves that ![]() $(V_1,\ldots,V_n)$ is an isometric dilation of
$(V_1,\ldots,V_n)$ is an isometric dilation of ![]() $(T_1,\ldots,T_n)$. Now (4.2) gives us
$(T_1,\ldots,T_n)$. Now (4.2) gives us ![]() $P_i+U_i^*P_jU_i=P_j+U_j^*P_iU_j$ for
$P_i+U_i^*P_jU_i=P_j+U_j^*P_iU_j$ for ![]() $1\leq i \lt j\leq n$ and condition (4) yields
$1\leq i \lt j\leq n$ and condition (4) yields ![]() $P_i+U_i^*P_jU_i=P_j+U_j^*P_iU_j\leq I_{\mathscr{D}_{T^*}}$. Hence, by an application of Lemma 3.2, we have that that
$P_i+U_i^*P_jU_i=P_j+U_j^*P_iU_j\leq I_{\mathscr{D}_{T^*}}$. Hence, by an application of Lemma 3.2, we have that that ![]() $ \prod_{i=1}^nV_i=M_z$, which is (up to a unitary) the minimal isometric dilation of T.
$ \prod_{i=1}^nV_i=M_z$, which is (up to a unitary) the minimal isometric dilation of T.
Conversely, suppose ![]() $(Y_1, \dots, Y_n)$ acting on
$(Y_1, \dots, Y_n)$ acting on ![]() $\mathscr{K}$ is an isometric dilation of
$\mathscr{K}$ is an isometric dilation of ![]() $(T_1, \dots, T_n)$, where
$(T_1, \dots, T_n)$, where ![]() $Y={\prod_{i=1}^nY_i}$ is the minimal isometric dilation of T. Let
$Y={\prod_{i=1}^nY_i}$ is the minimal isometric dilation of T. Let  $Y_i'={\prod_{j \neq i}Y_j}$ for
$Y_i'={\prod_{j \neq i}Y_j}$ for ![]() $1 \leq i \leq n$. Then,
$1 \leq i \leq n$. Then,
We first show that ![]() $Y_i^*|_{\mathscr{H}}=T_i^*$ for each
$Y_i^*|_{\mathscr{H}}=T_i^*$ for each ![]() $i=1, \dots, n$. Note that for any
$i=1, \dots, n$. Note that for any ![]() $i=1,\ldots,n$,
$i=1,\ldots,n$, ![]() $k\in \mathbb{N}\cup \{0 \}$ and
$k\in \mathbb{N}\cup \{0 \}$ and ![]() $h\in \mathscr{H}$,
$h\in \mathscr{H}$, ![]() $T_iP_{\mathscr{H}}(Y^kh) = T_iT^kh = P_{\mathscr{H}}Y_i(Y^kh) $, and as a consequence, we have
$T_iP_{\mathscr{H}}(Y^kh) = T_iT^kh = P_{\mathscr{H}}Y_i(Y^kh) $, and as a consequence, we have ![]() $T_iP_{\mathscr{H}}=P_{\mathscr{H}}Y_i$. Now, for any
$T_iP_{\mathscr{H}}=P_{\mathscr{H}}Y_i$. Now, for any ![]() $h\in \mathscr{H}$ and
$h\in \mathscr{H}$ and ![]() $k\in \mathscr{K}$,
$k\in \mathscr{K}$,
Hence, ![]() $Y_i|_{\mathscr{H}}=T_i$ for each i. Therefore, the block matrix form of each Yi with respect to the decomposition
$Y_i|_{\mathscr{H}}=T_i$ for each i. Therefore, the block matrix form of each Yi with respect to the decomposition ![]() $\mathscr{K} = \mathscr{H}\oplus {\mathscr{H}}^{\perp}$ is
$\mathscr{K} = \mathscr{H}\oplus {\mathscr{H}}^{\perp}$ is  $Y_i=\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}$ for some operators
$Y_i=\begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}$ for some operators ![]() $C_i,\, S_i$. Also, since
$C_i,\, S_i$. Also, since ![]() $Y=\Pi_{i=1}^n Y_i$, we have
$Y=\Pi_{i=1}^n Y_i$, we have  $Y=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}$ for some operators
$Y=\begin{bmatrix}
T&0\\
C&S
\end{bmatrix}$ for some operators ![]() $\,C,\, S $. Again
$\,C,\, S $. Again ![]() $V= {\prod_{i=1}^n V_i} = M_z$ on
$V= {\prod_{i=1}^n V_i} = M_z$ on ![]() $H^2(\mathscr{D}_{T^*})$ is also a minimal isometric dilation of T. Therefore,
$H^2(\mathscr{D}_{T^*})$ is also a minimal isometric dilation of T. Therefore,
Now the map ![]() $\tau :H^2(\mathscr{D}_{T^*})\to \mathscr{K}$ defined by
$\tau :H^2(\mathscr{D}_{T^*})\to \mathscr{K}$ defined by ![]() $\tau(V^nWh)=Y^nh$ is a unitary, which maps Wh to h and
$\tau(V^nWh)=Y^nh$ is a unitary, which maps Wh to h and ![]() $\tau^*$ maps h to Wh for all
$\tau^*$ maps h to Wh for all ![]() $h\in\mathscr{H}$. Therefore, with respect to the decomposition
$h\in\mathscr{H}$. Therefore, with respect to the decomposition ![]() $\mathscr{K}=\mathscr{H}\oplus \mathscr{H}^{\perp}$ and
$\mathscr{K}=\mathscr{H}\oplus \mathscr{H}^{\perp}$ and ![]() $H^2(\mathscr{D}_{T^*})=W(\mathscr{H})\oplus (W\mathscr{H})^{\perp}$ the map τ has block matrix form
$H^2(\mathscr{D}_{T^*})=W(\mathscr{H})\oplus (W\mathscr{H})^{\perp}$ the map τ has block matrix form  $\tau=\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix}$ for some unitary τ 1. Evidently,
$\tau=\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix}$ for some unitary τ 1. Evidently, ![]() $V=\tau^* Y \tau$. Now
$V=\tau^* Y \tau$. Now
 \begin{align*}
\tau^*Y_i\tau& = \begin{bmatrix}
W&0\\
0&\tau_{1}^*
\end{bmatrix} \begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix}\\
& = \begin{bmatrix}
WT_i&0\\
\tau_{1}^*C_i&\tau_{1}^*S_i
\end{bmatrix}\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix} = \begin{bmatrix}
WT_iW^*&0\\
\tau_{1}^*C_iW^*&\tau_{1}^*S_i\tau_{1}
\end{bmatrix}.
\end{align*}
\begin{align*}
\tau^*Y_i\tau& = \begin{bmatrix}
W&0\\
0&\tau_{1}^*
\end{bmatrix} \begin{bmatrix}
T_i&0\\
C_i&S_i
\end{bmatrix}\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix}\\
& = \begin{bmatrix}
WT_i&0\\
\tau_{1}^*C_i&\tau_{1}^*S_i
\end{bmatrix}\begin{bmatrix}
W^*&0\\
0&\tau_{1}
\end{bmatrix} = \begin{bmatrix}
WT_iW^*&0\\
\tau_{1}^*C_iW^*&\tau_{1}^*S_i\tau_{1}
\end{bmatrix}.
\end{align*} Therefore, ![]() $\tau^*V_i^*\tau(Wh)=WT_i^*W^*(Wh)=WT_i^*h$. For each
$\tau^*V_i^*\tau(Wh)=WT_i^*W^*(Wh)=WT_i^*h$. For each ![]() $i=1, \dots, n$, let us define
$i=1, \dots, n$, let us define ![]() $
\widehat{V}_i:=\tau^*V_i\tau $. Therefore,
$
\widehat{V}_i:=\tau^*V_i\tau $. Therefore,
 \begin{equation}
\widehat{V}_i^*Wh=WT_i^*h\, \quad \text{for all } \; h \in \mathscr{H},\qquad (1\leq i \leq n).
\end{equation}
\begin{equation}
\widehat{V}_i^*Wh=WT_i^*h\, \quad \text{for all } \; h \in \mathscr{H},\qquad (1\leq i \leq n).
\end{equation} Therefore,  $(\widehat{V}_1, \dots, \widehat{V}_n)=(\tau^*Y_1 \tau, \dots, \tau^* Y_n \tau)$ on
$(\widehat{V}_1, \dots, \widehat{V}_n)=(\tau^*Y_1 \tau, \dots, \tau^* Y_n \tau)$ on ![]() $H^2(\mathscr{D}_{T^*})$ is an isometric dilation of
$H^2(\mathscr{D}_{T^*})$ is an isometric dilation of ![]() $(T_1, \dots, T_n)$ such that
$(T_1, \dots, T_n)$ such that  ${\prod_{i=1}^n \widehat{V}_i}=V$. We now follow the arguments given in the converse part of the proof of Theorem 3.5. Since
${\prod_{i=1}^n \widehat{V}_i}=V$. We now follow the arguments given in the converse part of the proof of Theorem 3.5. Since ![]() $\widehat{V}_i$ is a commutant of
$\widehat{V}_i$ is a commutant of ![]() $V \;(=M_z)$,
$V \;(=M_z)$,  $\widehat{V}_i=M_{\phi_i}$, where
$\widehat{V}_i=M_{\phi_i}$, where ![]() $\phi_i(z)=F_i^{\prime *}+F_iz\in H^{\infty}(\mathscr{B}(\mathscr{D}_{T^*}))$. Evidently,
$\phi_i(z)=F_i^{\prime *}+F_iz\in H^{\infty}(\mathscr{B}(\mathscr{D}_{T^*}))$. Evidently, ![]() $U_i=F_i^*+F_i'$ and
$U_i=F_i^*+F_i'$ and ![]() $U_{i}'=F_i^*-F_i'$ are commuting unitaries and
$U_{i}'=F_i^*-F_i'$ are commuting unitaries and  $P_i=\dfrac{1}{2}(I-U_{i}^{\prime *}U_i)$ is a projection for all
$P_i=\dfrac{1}{2}(I-U_{i}^{\prime *}U_i)$ is a projection for all ![]() $i=1, \dots,n$. A simple computation shows that
$i=1, \dots,n$. A simple computation shows that ![]() $F_i=U_iP_i$ and
$F_i=U_iP_i$ and ![]() $F_i'=P_i^{\perp}U_i^*$. Also,
$F_i'=P_i^{\perp}U_i^*$. Also, ![]() $[F_i, F_j]=[F_i', F_j']=0$ for all
$[F_i, F_j]=[F_i', F_j']=0$ for all ![]() $i,j$. Therefore,
$i,j$. Therefore,
 \begin{equation*}
\widehat{V}_i=M_{U_iP_i^{\perp}+U_iP_iz} \qquad (1 \leq i \leq n).
\end{equation*}
\begin{equation*}
\widehat{V}_i=M_{U_iP_i^{\perp}+U_iP_iz} \qquad (1 \leq i \leq n).
\end{equation*} Obviously conditions (2) and (3) follow from the commutativity of ![]() $F_i, F_j$ and
$F_i, F_j$ and ![]() $F_i',F_j'$, respectively. It remains to show that conditions (1) and (4) hold. From (4.5), we have
$F_i',F_j'$, respectively. It remains to show that conditions (1) and (4) hold. From (4.5), we have  $\widehat{V}_i^*Wh=WT_i^*h$ for every
$\widehat{V}_i^*Wh=WT_i^*h$ for every ![]() $h \in \mathscr{H}$. Now for any
$h \in \mathscr{H}$. Now for any ![]() $h\in \mathscr{H}$, we have
$h\in \mathscr{H}$, we have
 \begin{align*}
\widehat{V}_i^*Wh&=\widehat{V}_i^*(\sum_{k=0}^{\infty}z^kD_{T^*}T^{*k}h )\\
&=P_i^{\perp}U_i^*D_{T^*}h+\sum_{k=1}^{\infty} z^kP_i^{\perp}U_i^*D_{T^*}T^{*k}h +z^{k-1}P_iU_i^*D_{T^*}T^{*k}h \\
&=\sum_{k=0}^{\infty}z^k(P_i^{\perp}U_i^*D_{T^*}T^{*k}+P_iU_i^*D_{T^*}T^{*(k+1)})h\\
&=\sum_{k=0}^{\infty}z^k(P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*)T^{*k}h.
\end{align*}
\begin{align*}
\widehat{V}_i^*Wh&=\widehat{V}_i^*(\sum_{k=0}^{\infty}z^kD_{T^*}T^{*k}h )\\
&=P_i^{\perp}U_i^*D_{T^*}h+\sum_{k=1}^{\infty} z^kP_i^{\perp}U_i^*D_{T^*}T^{*k}h +z^{k-1}P_iU_i^*D_{T^*}T^{*k}h \\
&=\sum_{k=0}^{\infty}z^k(P_i^{\perp}U_i^*D_{T^*}T^{*k}+P_iU_i^*D_{T^*}T^{*(k+1)})h\\
&=\sum_{k=0}^{\infty}z^k(P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*)T^{*k}h.
\end{align*}Also,
 \begin{equation*}
W(T_i^*h)=\sum_{k=0}^{\infty}z^kD_{T^*}T^{*k}T_i^*h =\sum_{k=0}^{\infty}z^kD_{T^*}T_i^*T^{*k}h.
\end{equation*}
\begin{equation*}
W(T_i^*h)=\sum_{k=0}^{\infty}z^kD_{T^*}T^{*k}T_i^*h =\sum_{k=0}^{\infty}z^kD_{T^*}T_i^*T^{*k}h.
\end{equation*} Comparing the constant terms, we have ![]() $
D_{T^*}T_i^* =P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*.
$ This proves condition (1). Now, since we have
$
D_{T^*}T_i^* =P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*.
$ This proves condition (1). Now, since we have  $ \prod_{i=1}^n\widehat{V}_i=V=M_z$ and
$ \prod_{i=1}^n\widehat{V}_i=V=M_z$ and  $\widehat{V}_i=M_{U_iP_i^{\perp}+zU_iP_i}$, condition (4) follows from Theorem 3.2. The uniqueness of
$\widehat{V}_i=M_{U_iP_i^{\perp}+zU_iP_i}$, condition (4) follows from Theorem 3.2. The uniqueness of ![]() $P_1, \dots, P_n$ and
$P_1, \dots, P_n$ and ![]() $U_1, \dots, U_n$ follows by an argument similar to that in the proof of the
$U_1, \dots, U_n$ follows by an argument similar to that in the proof of the ![]() $(\Rightarrow)$ part of Theorem 3.5. The proof is now complete.
$(\Rightarrow)$ part of Theorem 3.5. The proof is now complete.
Now we present an analogue of Theorem 3.9 when the product T is a ![]() $C._0$ contraction, and obviously, a proof follows from Theorem 4.1 and its proof.
$C._0$ contraction, and obviously, a proof follows from Theorem 4.1 and its proof.
Theorem 4.2 Let ![]() $T_1,\ldots, T_n \in \mathscr{B}(\mathscr{H})$ be commuting contractions such that
$T_1,\ldots, T_n \in \mathscr{B}(\mathscr{H})$ be commuting contractions such that ![]() $T=\prod_{i=1}^nT_i$ is a
$T=\prod_{i=1}^nT_i$ is a ![]() $C._0$ contraction. Then,
$C._0$ contraction. Then, ![]() $(T_1,\ldots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space of T if there are projections
$(T_1,\ldots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space of T if there are projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that the following hold for
$\mathscr{B}(\mathscr{D}_{T^*})$ such that the following hold for ![]() $i=1, \dots, n$:
$i=1, \dots, n$:
(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$.
$U_iP_iU_jP_j=U_jP_jU_iP_i$.
Conversely, if a commuting tuple of contractions ![]() $(T_1,\ldots,T_n)$, with the product
$(T_1,\ldots,T_n)$, with the product ![]() $T=\prod_{i=1}^n T_i$ being a
$T=\prod_{i=1}^n T_i$ being a ![]() $C._0$ contraction, possesses an isometric dilation
$C._0$ contraction, possesses an isometric dilation  $(\widehat{V}_1,\ldots,\widehat{V}_{n})$, where
$(\widehat{V}_1,\ldots,\widehat{V}_{n})$, where ![]() $V=\prod_{i=1}^nV_i$ is the minimal isometric dilation of T, then there are unique projections
$V=\prod_{i=1}^nV_i$ is the minimal isometric dilation of T, then there are unique projections ![]() $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ satisfying the conditions (1)–(3) above.
$\mathscr{B}(\mathscr{D}_{T^*})$ satisfying the conditions (1)–(3) above.
4.1. A functional model when the product is a  $C._0$ contraction
$C._0$ contraction
For a contraction T acting on a Hilbert space ![]() $\mathscr{H}$, let
$\mathscr{H}$, let ![]() $\Lambda_T$ be the set of all complex numbers for which the operator
$\Lambda_T$ be the set of all complex numbers for which the operator ![]() $I-zT^*$ is invertible. For
$I-zT^*$ is invertible. For ![]() $z\in \Lambda_T$, the characteristic function of T is defined as
$z\in \Lambda_T$, the characteristic function of T is defined as
 \begin{eqnarray}
\Theta_T(z)=[-T+zD_{T^*}(I-zT^*)^{-1}D_T]|_{\mathscr{D}_T}.
\end{eqnarray}
\begin{eqnarray}
\Theta_T(z)=[-T+zD_{T^*}(I-zT^*)^{-1}D_T]|_{\mathscr{D}_T}.
\end{eqnarray} Here, we recall a few definitions and terminologies from the initial part of § 3. The operators DT and ![]() $D_{T^*}$ are the defect operators
$D_{T^*}$ are the defect operators ![]() $(I-T^*T)^{1/2}$ and
$(I-T^*T)^{1/2}$ and ![]() $(I-TT^*)^{1/2}$, respectively. By virtue of the relation
$(I-TT^*)^{1/2}$, respectively. By virtue of the relation ![]() $TD_T=D_{T^*}T$ (section I.3 of [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]),
$TD_T=D_{T^*}T$ (section I.3 of [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]), ![]() $\Theta_T(z)$ maps
$\Theta_T(z)$ maps ![]() $\mathscr{D}_T=\overline{\textrm{Ran}}D_T$ into
$\mathscr{D}_T=\overline{\textrm{Ran}}D_T$ into ![]() $\mathscr{D}_{T^*}=\overline{\textrm{Ran}}D_{T^*}$ for every z in
$\mathscr{D}_{T^*}=\overline{\textrm{Ran}}D_{T^*}$ for every z in ![]() $\Lambda_T$.
$\Lambda_T$.
In [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17], Sz.-Nagy and Foias proved that every ![]() $C._0$ contraction P acting on
$C._0$ contraction P acting on ![]() $\mathscr{H}$ is unitarily equivalent to the operator
$\mathscr{H}$ is unitarily equivalent to the operator ![]() $\mathbb T=P_{\mathbb H_T}M_z|_{\mathbb H_T}$ on the Hilbert space
$\mathbb T=P_{\mathbb H_T}M_z|_{\mathbb H_T}$ on the Hilbert space  $\mathbb H_T=H^2(\mathscr{D}_{T^*}) \ominus M_{\Theta_T}(H^2(\mathscr{D}_T))$, where Mz is the multiplication operator on
$\mathbb H_T=H^2(\mathscr{D}_{T^*}) \ominus M_{\Theta_T}(H^2(\mathscr{D}_T))$, where Mz is the multiplication operator on ![]() $H^2(\mathscr{D}_{T^*})$ and
$H^2(\mathscr{D}_{T^*})$ and ![]() $M_{\Theta_T}$ is the multiplication operator from
$M_{\Theta_T}$ is the multiplication operator from ![]() $H^2( \mathscr{D}_T)$ into
$H^2( \mathscr{D}_T)$ into ![]() $H^2(\mathscr{D}_{T^*})$ corresponding to the multiplier
$H^2(\mathscr{D}_{T^*})$ corresponding to the multiplier ![]() $\Theta_T$. This is known as Sz. Nagy–Foias model for a
$\Theta_T$. This is known as Sz. Nagy–Foias model for a ![]() $C._0$ contraction. Indeed, Mz on
$C._0$ contraction. Indeed, Mz on ![]() $H^2(\mathscr{D}_{T^*})$ dilates
$H^2(\mathscr{D}_{T^*})$ dilates ![]() $T \in \mathscr{B}(\mathscr{H})$, and
$T \in \mathscr{B}(\mathscr{H})$, and ![]() $W: \mathscr{H} \rightarrow H^2(\mathscr{D}_{T^*})$ as in (4.4) is the concerned isometric embedding. In an analogous manner by an application of Theorem 4.1, we obtain a functional model for a tuple of commuting contractions with
$W: \mathscr{H} \rightarrow H^2(\mathscr{D}_{T^*})$ as in (4.4) is the concerned isometric embedding. In an analogous manner by an application of Theorem 4.1, we obtain a functional model for a tuple of commuting contractions with ![]() $C._0$ product. A notable fact about this model is that the multiplication operators involved in this model have analytic symbols which are linear functions in one variable.
$C._0$ product. A notable fact about this model is that the multiplication operators involved in this model have analytic symbols which are linear functions in one variable.
Theorem 4.3 Let ![]() $T_1,\ldots,T_n$ be commuting contractions on a Hilbert space
$T_1,\ldots,T_n$ be commuting contractions on a Hilbert space ![]() $\mathscr{H}$ such that their product
$\mathscr{H}$ such that their product ![]() $T=\Pi_{i=1}^nT_i$ is a
$T=\Pi_{i=1}^nT_i$ is a ![]() $C._0$ contraction. If there are projections
$C._0$ contraction. If there are projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ satisfying the following for
$\mathscr{B}(\mathscr{D}_{T^*})$ satisfying the following for ![]() $1 \leq i \leq n$:
$1 \leq i \leq n$:
(1)
 $D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,
$D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,
then ![]() $(T_1, \dots, T_n)$ is unitarily equivalent to
$(T_1, \dots, T_n)$ is unitarily equivalent to  $(\widetilde{T}_1, \dots, \widetilde{T}_n)$ acting on the space
$(\widetilde{T}_1, \dots, \widetilde{T}_n)$ acting on the space  $\mathbb H_T=H^2(\mathscr{D}_{T^*})\ominus M_{\Theta_T}(H^2(\mathscr{D}_T))$, where
$\mathbb H_T=H^2(\mathscr{D}_{T^*})\ominus M_{\Theta_T}(H^2(\mathscr{D}_T))$, where  $\widetilde{T}_i=P_{\mathbb H_T}(M_{U_iP_i^{\perp}+zU_iP_i})|_{\mathbb H_T}$ for
$\widetilde{T}_i=P_{\mathbb H_T}(M_{U_iP_i^{\perp}+zU_iP_i})|_{\mathbb H_T}$ for ![]() $1\leq i \leq n$.
$1\leq i \leq n$.
Proof. For a ![]() $C._0$ contraction T, we have from literature (e.g., [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17] or lemma 3.3 in [Reference Bhattacharyya and Pal21]) that
$C._0$ contraction T, we have from literature (e.g., [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17] or lemma 3.3 in [Reference Bhattacharyya and Pal21]) that
 \begin{equation*}
WW^*+M_{\Theta_T}M_{\Theta_T}^*=I_{H^2(\mathscr{D}_{P^*})}.
\end{equation*}
\begin{equation*}
WW^*+M_{\Theta_T}M_{\Theta_T}^*=I_{H^2(\mathscr{D}_{P^*})}.
\end{equation*} It follows from here that ![]() $W(\mathscr{H})=\mathbb H_T$, where
$W(\mathscr{H})=\mathbb H_T$, where ![]() $W: \mathscr{H} \rightarrow H^2(\mathscr{D}_{T^*})$ is as in (4.4). Since
$W: \mathscr{H} \rightarrow H^2(\mathscr{D}_{T^*})$ is as in (4.4). Since ![]() $V_i^*|_{W(\mathscr{H})}=T_i^*$, where
$V_i^*|_{W(\mathscr{H})}=T_i^*$, where  $V_i=(M_{U_iP_i^{\perp}+zU_iP_i})$, we have that
$V_i=(M_{U_iP_i^{\perp}+zU_iP_i})$, we have that  $T_i \cong P_{\mathbb H_T}(M_{U_iP_i^{\perp}+zU_iP_i})|_{\mathbb H_T}$ for
$T_i \cong P_{\mathbb H_T}(M_{U_iP_i^{\perp}+zU_iP_i})|_{\mathbb H_T}$ for ![]() $i=1, \dots, n$.
$i=1, \dots, n$.
4.2. A factorization of a  $C._0$ contraction
$C._0$ contraction
The model for commuting n-isometries, Theorem 3.2, can be restated in the following way.
Theorem 4.4 Let ![]() $V_1,\dots,V_n$ be commuting isometries acting on a Hilbert space
$V_1,\dots,V_n$ be commuting isometries acting on a Hilbert space ![]() $\mathscr{H}$ and let
$\mathscr{H}$ and let ![]() $V=\prod_{i=1}^nV_i$. Then,
$V=\prod_{i=1}^nV_i$. Then, ![]() $V=\prod_{i=1}^nV_i$ is a pure isometry if and only if there are unique orthogonal projections
$V=\prod_{i=1}^nV_i$ is a pure isometry if and only if there are unique orthogonal projections ![]() $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{V^*})$ with
$\mathscr{B}(\mathscr{D}_{V^*})$ with ![]() $\prod_{i=1}^n U_i=I$ such that the following conditions hold for
$\prod_{i=1}^n U_i=I$ such that the following conditions hold for ![]() $i=1, \dots, n$:
$i=1, \dots, n$:
(1)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(2)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(3)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
Moreover, ![]() $(V_1, \dots, V_n)$ is unitarily equivalent to
$(V_1, \dots, V_n)$ is unitarily equivalent to  $(M_{U_1P_1^{\perp}+zU_1P_1}, \dots, M_{U_nP_n^{\perp}+zU_nP_n})$ on
$(M_{U_1P_1^{\perp}+zU_1P_1}, \dots, M_{U_nP_n^{\perp}+zU_nP_n})$ on ![]() $H^2(\mathscr{D}_{V^*})$.
$H^2(\mathscr{D}_{V^*})$.
Proof. First, suppose ![]() $(V_1,\dots, V_n )$ on Hilbert space
$(V_1,\dots, V_n )$ on Hilbert space ![]() $\mathscr{H}$ is a commuting n-tuple of isometries with
$\mathscr{H}$ is a commuting n-tuple of isometries with ![]() $\prod_{i=1}^nV_i=V$ being a pure isometry. Thus,
$\prod_{i=1}^nV_i=V$ being a pure isometry. Thus, ![]() $\mathscr{H}$ can be identified with
$\mathscr{H}$ can be identified with ![]() $H^2(\mathscr{D}_{V^*})$ via a unitary
$H^2(\mathscr{D}_{V^*})$ via a unitary ![]() $\tau:\mathscr{H}\to H^2(\mathscr{D}_{V^*})$, and V can be identified with Mz on
$\tau:\mathscr{H}\to H^2(\mathscr{D}_{V^*})$, and V can be identified with Mz on ![]() $H^2(\mathscr{D}_{V^*})$. Let
$H^2(\mathscr{D}_{V^*})$. Let ![]() $\widehat{V}_i=\tau V_i \tau^*$ for
$\widehat{V}_i=\tau V_i \tau^*$ for ![]() $i=1,2\dots, n $. Hence,
$i=1,2\dots, n $. Hence,  $(\widehat{V}_1, \dots,\widehat{V}_n )$ is a commuting n-tuple of isometries with
$(\widehat{V}_1, \dots,\widehat{V}_n )$ is a commuting n-tuple of isometries with  $\prod_{i=1}^n\widehat{V}_i=M_z$ on
$\prod_{i=1}^n\widehat{V}_i=M_z$ on ![]() $H^2(\mathscr{D}_{V^*})$. Therefore,
$H^2(\mathscr{D}_{V^*})$. Therefore,  $(\widehat{V}_1,\dots,\widehat{V}_n)$ is an isometric dilation of
$(\widehat{V}_1,\dots,\widehat{V}_n)$ is an isometric dilation of ![]() $(V_1,\dots,V_n)$ with Mz being the minimal isometric dilation of V. Therefore, by Theorem 4.1, there are unique commuting unitaries
$(V_1,\dots,V_n)$ with Mz being the minimal isometric dilation of V. Therefore, by Theorem 4.1, there are unique commuting unitaries ![]() $U_1,\dots, U_n$ and unique orthogonal projections
$U_1,\dots, U_n$ and unique orthogonal projections ![]() $P_1,\dots P_n$ in
$P_1,\dots P_n$ in ![]() $\mathscr{B}(\mathscr{D}_{V^*})$ such that
$\mathscr{B}(\mathscr{D}_{V^*})$ such that ![]() $\prod_{i=1}^nU_i=I$ and that the conditions (1)–(3) are satisfied.
$\prod_{i=1}^nU_i=I$ and that the conditions (1)–(3) are satisfied.
Conversely, suppose there are unique orthogonal projections ![]() $P_1,\ldots,P_n$ and unique commuting unitaries
$P_1,\ldots,P_n$ and unique commuting unitaries ![]() $U_1,\ldots,U_n$ in
$U_1,\ldots,U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{V^*})$ such that
$\mathscr{B}(\mathscr{D}_{V^*})$ such that ![]() $\prod_{i=1}^n U_i=I$ and that the conditions (1)–(3) are satisfied. Let
$\prod_{i=1}^n U_i=I$ and that the conditions (1)–(3) are satisfied. Let  $V_i=M_{U_iP_i^{\perp}+zU_iP_i}$ for each
$V_i=M_{U_iP_i^{\perp}+zU_iP_i}$ for each ![]() $i=1,2\dots,n$. Then, as seen in the proof of Theorem 4.1,
$i=1,2\dots,n$. Then, as seen in the proof of Theorem 4.1, ![]() $(V_1,\dots, V_n) $ is a commuting n-tuple of isometries with
$(V_1,\dots, V_n) $ is a commuting n-tuple of isometries with ![]() $\prod_{i=1}^nV_i=M_z$ on
$\prod_{i=1}^nV_i=M_z$ on ![]() $H^2(\mathscr{D}_{V^*})$.
$H^2(\mathscr{D}_{V^*})$.
Also, Theorem 3.2 provides a factorization of a ![]() $C._0$ isometry (i.e., a pure isometry) in terms of n number of commuting isometries. Our result, Theorem 4.1, gives a factorization of a
$C._0$ isometry (i.e., a pure isometry) in terms of n number of commuting isometries. Our result, Theorem 4.1, gives a factorization of a ![]() $C._0$ contraction in the following way:
$C._0$ contraction in the following way:
Theorem 4.5 Let ![]() $T_1,\ldots,T_n$ be commuting contractions on a Hilbert space
$T_1,\ldots,T_n$ be commuting contractions on a Hilbert space ![]() $\mathscr{H}$ and let their product
$\mathscr{H}$ and let their product ![]() $T=\prod_{i=1}^n T_i$ be a
$T=\prod_{i=1}^n T_i$ be a ![]() $C._0$ contraction. Then,
$C._0$ contraction. Then, ![]() $(T_1^*, \dots, T_n^*)\equiv (V_1^*|_{\mathscr{H}}, \dots, V_n^*|_{\mathscr{H}})$ for a model n-isometry
$(T_1^*, \dots, T_n^*)\equiv (V_1^*|_{\mathscr{H}}, \dots, V_n^*|_{\mathscr{H}})$ for a model n-isometry ![]() $(V_1, \dots, V_n)$ on
$(V_1, \dots, V_n)$ on ![]() $H^2(\mathscr{D}_{T^*})$ if and only if there exist unique orthogonal projections
$H^2(\mathscr{D}_{T^*})$ if and only if there exist unique orthogonal projections ![]() $P_1, \dots, P_n$ and unique commuting unitaries
$P_1, \dots, P_n$ and unique commuting unitaries ![]() $U_1, \dots, U_n$ in
$U_1, \dots, U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that
$\mathscr{B}(\mathscr{D}_{T^*})$ such that  $\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and the following conditions are satisfied:
$\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and the following conditions are satisfied:
(1)
 $D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,
$D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
$P_1+U_1^*P_2U_1+U_1^*U_2^*P_3U_2U_1+\ldots +U_1^*U_2^*\ldots U_{n-1}^*P_nU_{n-1}\ldots U_2U_1 =I_{\mathscr{D}_T}$.
Proof. First suppose there are projections ![]() $P_1, \dots, P_n$ and commuting unitaries
$P_1, \dots, P_n$ and commuting unitaries ![]() $U_1, \dots, U_n$ in
$U_1, \dots, U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that
$\mathscr{B}(\mathscr{D}_{T^*})$ such that  $\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and that the conditions (1)–(4) are satisfied. Then, Theorem 4.1 provides commuting n-isometries
$\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and that the conditions (1)–(4) are satisfied. Then, Theorem 4.1 provides commuting n-isometries ![]() $V_1, \dots, V_n$ on
$V_1, \dots, V_n$ on ![]() $H^2(\mathscr{D}_{T^*})$ with
$H^2(\mathscr{D}_{T^*})$ with  $V_i=M_{U_iP_i^{\perp}+zU_iP_i}$ for each i such that
$V_i=M_{U_iP_i^{\perp}+zU_iP_i}$ for each i such that
where W is the isometry as in (4.4).
Conversely, suppose ![]() $(T_1^*,\ldots,T_n^*)$ is equivalent to
$(T_1^*,\ldots,T_n^*)$ is equivalent to ![]() $(V_1^*|_{\mathscr{H}},\ldots,V_n^*|_{\mathscr{H}})$ for some model n-isometry
$(V_1^*|_{\mathscr{H}},\ldots,V_n^*|_{\mathscr{H}})$ for some model n-isometry ![]() $(V_1,\ldots,V_n)$ on
$(V_1,\ldots,V_n)$ on ![]() $H^2(\mathscr{D}_{T^*})$. Then, by the
$H^2(\mathscr{D}_{T^*})$. Then, by the ![]() $(\Rightarrow)$ part of Theorem 4.1, there are projections
$(\Rightarrow)$ part of Theorem 4.1, there are projections ![]() $P_1, \dots, P_n$ and commuting unitaries
$P_1, \dots, P_n$ and commuting unitaries ![]() $U_1, \dots, U_n$ in
$U_1, \dots, U_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that
$\mathscr{B}(\mathscr{D}_{T^*})$ such that  $\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and that the conditions (1)–(4) are satisfied.
$\prod_{i=1}^n U_i=I_{\mathscr{D}_{T^*}}$ and that the conditions (1)–(4) are satisfied.
5. Examples
In this section, we present several examples to compare our classes of commuting contractions admitting isometric dilation with the previously determined various classes from the literature. We shall show that neither our classes are properly contained in any of these classes from the literature nor any previously determined classes are contained properly in our classes. However, there are always non-trivial intersections. Note that our theory is one-dimensional in the sense that the operator models that we obtained are all having multiplication operators with multipliers of one complex variable.
Suppose ![]() $(T_1,T_2)$ is a commuting pair of contractions admitting isometric dilation
$(T_1,T_2)$ is a commuting pair of contractions admitting isometric dilation ![]() $(V_1,V_2)$ on the minimal dilation space of
$(V_1,V_2)$ on the minimal dilation space of ![]() $T=T_1T_2$. If there are unitaries
$T=T_1T_2$. If there are unitaries ![]() $U_1,U_2$ and projections
$U_1,U_2$ and projections ![]() $P_1,P_2$ such that
$P_1,P_2$ such that ![]() $U_iP_j=U_jP_i$ for
$U_iP_j=U_jP_i$ for ![]() $i=1,2$ and that the condition (1) of Theorem 3.9 holds, then it can be verified that the conditions (2),(3), and(4) hold as a consequence. Hence,
$i=1,2$ and that the condition (1) of Theorem 3.9 holds, then it can be verified that the conditions (2),(3), and(4) hold as a consequence. Hence, ![]() $(T_1,T_2)$ has an isometric dilation on the minimal isometric dilation space of T. Now one may ask a question: if
$(T_1,T_2)$ has an isometric dilation on the minimal isometric dilation space of T. Now one may ask a question: if ![]() $(T_1,T_2)$ admits isometric dilation on the minimal isometric dilation space of T, then will the corresponding unitaries commute with the projections? The following example gives a negative answer to this:
$(T_1,T_2)$ admits isometric dilation on the minimal isometric dilation space of T, then will the corresponding unitaries commute with the projections? The following example gives a negative answer to this:
Example 5.1. Let  $T_1=T_2=\begin{bmatrix}
0&1\\
0&0
\end{bmatrix}$ be commuting pair of contractions on
$T_1=T_2=\begin{bmatrix}
0&1\\
0&0
\end{bmatrix}$ be commuting pair of contractions on ![]() $\mathbb{C}^2$. Then, clearly,
$\mathbb{C}^2$. Then, clearly, ![]() $T=T_1T_2=0$, and hence,
$T=T_1T_2=0$, and hence, ![]() $D_T=I$. Hence, we need to find commuting
$D_T=I$. Hence, we need to find commuting ![]() $U_1,U_2$ and projections
$U_1,U_2$ and projections ![]() $P_1,P_2$ such that
$P_1,P_2$ such that ![]() $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$ for
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$ for ![]() $i=1,2$. Substituting
$i=1,2$. Substituting ![]() $D_T=I$ and T = 0, the above equations are equivalent to
$D_T=I$ and T = 0, the above equations are equivalent to ![]() $T_1=P_1^{\perp}U_1^* $ and
$T_1=P_1^{\perp}U_1^* $ and ![]() $T_2=P_2^{\perp}U_2^*$. One can observe that
$T_2=P_2^{\perp}U_2^*$. One can observe that  $P_1=P_2=\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}$ and
$P_1=P_2=\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}$ and  $U_1=U_2=\begin{bmatrix}
0&1\\1&0
\end{bmatrix}$ satisfy the above two equations. It is clear that
$U_1=U_2=\begin{bmatrix}
0&1\\1&0
\end{bmatrix}$ satisfy the above two equations. It is clear that ![]() $U_1, U_2$ are commuting unitaries and
$U_1, U_2$ are commuting unitaries and ![]() $P_1, P_2$ are projections. Further as
$P_1, P_2$ are projections. Further as ![]() $T_1,T_2$ commute with each other, it follows that
$T_1,T_2$ commute with each other, it follows that ![]() $P_1^{\perp}U_1^*$ commutes with
$P_1^{\perp}U_1^*$ commutes with ![]() $P_2^{\perp}U_2^*$. Simple calculation shows that
$P_2^{\perp}U_2^*$. Simple calculation shows that ![]() $U_1P_1=T_1$ and
$U_1P_1=T_1$ and ![]() $U_2P_2=T_2$. Therefore,
$U_2P_2=T_2$. Therefore, ![]() $U_1P_1$ commutes with
$U_1P_1$ commutes with ![]() $U_2P_2$. Further
$U_2P_2$. Further  $D_TU_iP_iU_i^*D_T=U_iP_iU_i^*=U_iP_iP_iU_i^*=T_iT_i^*=\begin{bmatrix}
1&0\\0&0
\end{bmatrix}=D_{T_i}^2.$ Also
$D_TU_iP_iU_i^*D_T=U_iP_iU_i^*=U_iP_iP_iU_i^*=T_iT_i^*=\begin{bmatrix}
1&0\\0&0
\end{bmatrix}=D_{T_i}^2.$ Also ![]() $P_1+U_1^*P_2U_1=I$. Hence, the conditions (1)–(5) of Theorem 3.5 hold. But one can clearly observe that Ui do not commute with Pj as
$P_1+U_1^*P_2U_1=I$. Hence, the conditions (1)–(5) of Theorem 3.5 hold. But one can clearly observe that Ui do not commute with Pj as  $U_iP_j=\begin{bmatrix}
0&1\\0&0
\end{bmatrix}$ and
$U_iP_j=\begin{bmatrix}
0&1\\0&0
\end{bmatrix}$ and  $P_jU_i=\begin{bmatrix}
0&0\\1&0
\end{bmatrix}$.
$P_jU_i=\begin{bmatrix}
0&0\\1&0
\end{bmatrix}$.
Before going to the next example let us note down the following observation from the proofs of the previously stated dilation theorems:
Note 5.2.
Let ![]() $T_1,\dots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions. Suppose there are projections
$T_1,\dots,T_n\in \mathscr{B}(\mathscr{H})$ be commuting contractions. Suppose there are projections ![]() $P_1,\dots,P_n\in \mathscr{B}(\mathscr{D}_T)$ and commuting unitaries
$P_1,\dots,P_n\in \mathscr{B}(\mathscr{D}_T)$ and commuting unitaries ![]() $U_1,\dots,U_n\in\mathscr{B}(\mathscr{D}_T)$ such that
$U_1,\dots,U_n\in\mathscr{B}(\mathscr{D}_T)$ such that ![]() $\prod_{i=1}^nU_i=I$ and conditions (1)–(5) of Theorem 3.5 are satisfied. Then, by Theorem 3.5,
$\prod_{i=1}^nU_i=I$ and conditions (1)–(5) of Theorem 3.5 are satisfied. Then, by Theorem 3.5, ![]() $(T_1,\dots,T_n)$ possesses an isometric dilation
$(T_1,\dots,T_n)$ possesses an isometric dilation ![]() $(V_1,\dots,V_n)$ on the minimal isometric dilation space
$(V_1,\dots,V_n)$ on the minimal isometric dilation space ![]() $\mathscr{K}$ of T such that
$\mathscr{K}$ of T such that ![]() $\prod_{i=1}^nV_i=V$ is the minimal isometric dilation of T. Without loss of generality, we can assume Vi to be as in (3.3) and V to be the Schäffer’s minimal isometric dilation. So, if
$\prod_{i=1}^nV_i=V$ is the minimal isometric dilation of T. Without loss of generality, we can assume Vi to be as in (3.3) and V to be the Schäffer’s minimal isometric dilation. So, if  $V_i'=\prod_{j\neq i}V_j$, then
$V_i'=\prod_{j\neq i}V_j$, then
 \begin{equation*}
{V}_i'= V_i^*V=\begin{bmatrix}
T_i'&0&0&0&\ldots \\
U_iP_i^{\perp}D_T&U_iP_i&0&0&\ldots \\
0&U_iP_i^{\perp}&U_iP_i&0&\ldots \\
0&0&U_iP_i^{\perp}&U_iP_i&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}.
\end{equation*}
\begin{equation*}
{V}_i'= V_i^*V=\begin{bmatrix}
T_i'&0&0&0&\ldots \\
U_iP_i^{\perp}D_T&U_iP_i&0&0&\ldots \\
0&U_iP_i^{\perp}&U_iP_i&0&\ldots \\
0&0&U_iP_i^{\perp}&U_iP_i&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix}.
\end{equation*} Thus, ![]() $(2,1)$ entries of both sides of
$(2,1)$ entries of both sides of ![]() ${V}_i'{V}={V}{V}_i' $ give
${V}_i'{V}={V}{V}_i' $ give ![]() $D_TT_i'=U_iP_iD_T+U_iP_i^{\perp}D_TT$ for
$D_TT_i'=U_iP_iD_T+U_iP_i^{\perp}D_TT$ for ![]() $1\leq i \leq n$.
$1\leq i \leq n$.
Let ![]() $\mathscr{U}^n(\mathscr{H}) $ be the class of commuting n-tuples of contractions on
$\mathscr{U}^n(\mathscr{H}) $ be the class of commuting n-tuples of contractions on ![]() $\mathscr{H}$ satisfying conditions (1)–(4) of Theorem 3.9 and let
$\mathscr{H}$ satisfying conditions (1)–(4) of Theorem 3.9 and let ![]() $\mathscr{S}^n(\mathscr{H})$ denote the class satisfying conditions (1)–(5) of Theorem 3.5. The following example shows that
$\mathscr{S}^n(\mathscr{H})$ denote the class satisfying conditions (1)–(5) of Theorem 3.5. The following example shows that ![]() $\mathscr{S}^n(\mathscr{H})$ is properly contained in
$\mathscr{S}^n(\mathscr{H})$ is properly contained in ![]() $\mathscr{U}^n(\mathscr{H})$.
$\mathscr{U}^n(\mathscr{H})$.
Example 5.3. Let us consider the following doubly commuting contractions acting on ![]() $\mathbb{C}^3$:
$\mathbb{C}^3$:
 \begin{equation*}
T_1=\begin{bmatrix}
1&0&0\\0&0&0\\0&0&0
\end{bmatrix}, \;
T_2=\begin{bmatrix}
0&0&0\\0&1&0\\0&0&0
\end{bmatrix}, \;
T_3=\begin{bmatrix}
0&0&0\\0&0&0\\0&0&1
\end{bmatrix}.
\end{equation*}
\begin{equation*}
T_1=\begin{bmatrix}
1&0&0\\0&0&0\\0&0&0
\end{bmatrix}, \;
T_2=\begin{bmatrix}
0&0&0\\0&1&0\\0&0&0
\end{bmatrix}, \;
T_3=\begin{bmatrix}
0&0&0\\0&0&0\\0&0&1
\end{bmatrix}.
\end{equation*} We show that ![]() $(T_1,T_2,T_3)\notin \mathscr{S}^3(\mathbb{C}^3)$ though it belongs to
$(T_1,T_2,T_3)\notin \mathscr{S}^3(\mathbb{C}^3)$ though it belongs to ![]() $ \mathscr{U}^3(\mathbb{C}^3) $. Note that
$ \mathscr{U}^3(\mathbb{C}^3) $. Note that ![]() $T_1'=T_2T_3=0$ and similarly
$T_1'=T_2T_3=0$ and similarly ![]() $T_2'=T_3'=0$. Also, it is clear that
$T_2'=T_3'=0$. Also, it is clear that ![]() $T=T_1T_2T_3=0$, and hence,
$T=T_1T_2T_3=0$, and hence, ![]() $D_T=I$ on
$D_T=I$ on ![]() $\mathbb{C}^3$. Thus,
$\mathbb{C}^3$. Thus, ![]() $\mathscr{D}_T=\mathbb{C}^3$. Now suppose there are commuting unitaries
$\mathscr{D}_T=\mathbb{C}^3$. Now suppose there are commuting unitaries ![]() $U_1,U_2,U_3$ and projections
$U_1,U_2,U_3$ and projections ![]() $P_1,P_2,P_3$ in
$P_1,P_2,P_3$ in ![]() $\mathscr{B}(\mathbb{C}^3)$ satisfying the hypotheses of Theorem 3.5. Then, for each i, we have that
$\mathscr{B}(\mathbb{C}^3)$ satisfying the hypotheses of Theorem 3.5. Then, for each i, we have that ![]() $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$. Since T = 0 and
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$. Since T = 0 and ![]() $D_T=I$, it reduces to
$D_T=I$, it reduces to ![]() $T_i=P_i^{\perp}U_i^*$. Again, from Note 5.2, it is clear that the unitaries and projections satisfying (1)–(5) must also satisfy
$T_i=P_i^{\perp}U_i^*$. Again, from Note 5.2, it is clear that the unitaries and projections satisfying (1)–(5) must also satisfy ![]() $D_TT_i'=U_iP_iD_T+U_i^*P_i^{\perp}D_TT$, which is same as saying that
$D_TT_i'=U_iP_iD_T+U_i^*P_i^{\perp}D_TT$, which is same as saying that ![]() $T_i'=U_iP_i$. Thus,
$T_i'=U_iP_i$. Thus, ![]() $T_i^*+T_i'=U_iP_i^{\perp}+U_iP_i=U_i$. Since
$T_i^*+T_i'=U_iP_i^{\perp}+U_iP_i=U_i$. Since ![]() $T_i'=0$, we have that
$T_i'=0$, we have that ![]() $U_i=T_i^*+T_i'=T_i^*$. This contradicts the fact that Ui is a unitary. Hence,
$U_i=T_i^*+T_i'=T_i^*$. This contradicts the fact that Ui is a unitary. Hence, ![]() $(T_1,T_2,T_3)\notin \mathscr{S}^3(\mathbb{C}^3)$. Now if we take
$(T_1,T_2,T_3)\notin \mathscr{S}^3(\mathbb{C}^3)$. Now if we take ![]() $U_i=I$ and
$U_i=I$ and ![]() $P_i=I-T_i$ for
$P_i=I-T_i$ for ![]() $i=1,2,3$, then one can easily verify that the conditions (1)–(4) of Theorem 3.9 hold.
$i=1,2,3$, then one can easily verify that the conditions (1)–(4) of Theorem 3.9 hold.
In [Reference Barik, Das, Haria and Sarkar15], Barik, Das, Haria, and Sarkar introduced a new class of commuting contractions that admit isometric dilation. For each natural number ![]() $n\geq 3$ and for every number
$n\geq 3$ and for every number ![]() $p,q$ with
$p,q$ with ![]() $1\leq p \lt q \leq n$, let
$1\leq p \lt q \leq n$, let ![]() $\mathscr{T}^n_{p,q}(\mathscr{H})$ be defined as follows:
$\mathscr{T}^n_{p,q}(\mathscr{H})$ be defined as follows:
 \begin{equation}
\mathscr{T}^n_{p,q}(\mathscr{H})=\{T\in \mathscr{T}^n(\mathscr{H}):\hat{T}_p,\hat{T}_q\in \mathbb{S}_{n-1}(\mathscr{H}),\,\text{and } \hat{T}_p \text{is pure} \}, \
\end{equation}
\begin{equation}
\mathscr{T}^n_{p,q}(\mathscr{H})=\{T\in \mathscr{T}^n(\mathscr{H}):\hat{T}_p,\hat{T}_q\in \mathbb{S}_{n-1}(\mathscr{H}),\,\text{and } \hat{T}_p \text{is pure} \}, \
\end{equation} where for any natural number ![]() $i\leq n$,
$i\leq n$,  $\hat{T}_i=(T_1,\ldots,T_{i-1},T_{i+1},\ldots T_n)$,
$\hat{T}_i=(T_1,\ldots,T_{i-1},T_{i+1},\ldots T_n)$, ![]() $\mathscr{T}_{n}(\mathscr{H})$ is a set of commuting n-tuple of contractions on space
$\mathscr{T}_{n}(\mathscr{H})$ is a set of commuting n-tuple of contractions on space ![]() $\mathscr{H}$ and
$\mathscr{H}$ and
 \begin{equation*}
\mathbb{S}_n(\mathscr{H})=\{T\in \mathscr{T}^n(\mathscr{H}):\sum_{k\in \{0,1\}^n}(-1)^{|k|}T^kT^{*k} \geq 0\} .
\end{equation*}
\begin{equation*}
\mathbb{S}_n(\mathscr{H})=\{T\in \mathscr{T}^n(\mathscr{H}):\sum_{k\in \{0,1\}^n}(-1)^{|k|}T^kT^{*k} \geq 0\} .
\end{equation*} Note that ![]() $\mathbb{S}_n(\mathscr{H})$ is the set of all those n-tuples of contractions on
$\mathbb{S}_n(\mathscr{H})$ is the set of all those n-tuples of contractions on ![]() $\mathscr{H}$ that satisfy Szego positivity condition, i.e.,
$\mathscr{H}$ that satisfy Szego positivity condition, i.e.,  $\sum_{k\in \{0,1\}^n}(-1)^{|k|}T^kT^{*k} \geq 0$. The class obtained by putting an additional condition
$\sum_{k\in \{0,1\}^n}(-1)^{|k|}T^kT^{*k} \geq 0$. The class obtained by putting an additional condition ![]() $\|T_i\| \lt 1$ for each i on the elements of
$\|T_i\| \lt 1$ for each i on the elements of ![]() $\mathscr{T}^n_{p,q}(\mathscr{H})$ is denoted by
$\mathscr{T}^n_{p,q}(\mathscr{H})$ is denoted by ![]() $\mathscr{P}^n_{p,q}(\mathscr{H})$. This class has been studied in [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] by Grinshpan, Kaliuzhnyi, Verbovetskyi, Vinnikov, and Woerdeman. In [Reference Barik, Das, Haria and Sarkar15], it is shown that
$\mathscr{P}^n_{p,q}(\mathscr{H})$. This class has been studied in [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] by Grinshpan, Kaliuzhnyi, Verbovetskyi, Vinnikov, and Woerdeman. In [Reference Barik, Das, Haria and Sarkar15], it is shown that ![]() $\mathscr{P}^n_{p,q}(\mathscr{H})\subsetneq \mathscr{T}^n_{p,q}(\mathscr{H})$ for
$\mathscr{P}^n_{p,q}(\mathscr{H})\subsetneq \mathscr{T}^n_{p,q}(\mathscr{H})$ for ![]() $1\leq p \lt q \leq n$. The following example shows that an element of our class may not satisfy the Szego positivity condition.
$1\leq p \lt q \leq n$. The following example shows that an element of our class may not satisfy the Szego positivity condition.
Example 5.4. Let  $T_1=T_2=\begin{bmatrix}
0&0\\
1&0
\end{bmatrix}$ and
$T_1=T_2=\begin{bmatrix}
0&0\\
1&0
\end{bmatrix}$ and ![]() $T_3=I$. Then,
$T_3=I$. Then, ![]() $T=T_1T_2T_3=0$, and hence,
$T=T_1T_2T_3=0$, and hence, ![]() $D_{T}=I$. Let
$D_{T}=I$. Let  $P_1=P_2=\begin{bmatrix}
1&0\\
0&0
\end{bmatrix}$,
$P_1=P_2=\begin{bmatrix}
1&0\\
0&0
\end{bmatrix}$, ![]() $P_3=0$ and
$P_3=0$ and  $U_1=U_2= \begin{bmatrix}
0&1\\
1&0
\end{bmatrix} $,
$U_1=U_2= \begin{bmatrix}
0&1\\
1&0
\end{bmatrix} $, ![]() $U_3=I$. Then
$U_3=I$. Then ![]() $U_1,U_2,U_3$ are commuting unitaries and
$U_1,U_2,U_3$ are commuting unitaries and ![]() $P_1,P_2,P_3$ are projections satisfying
$P_1,P_2,P_3$ are projections satisfying ![]() $U_1U_2U_3=I$ and the conditions (1)–(5) of Theorem 3.5. Hence,
$U_1U_2U_3=I$ and the conditions (1)–(5) of Theorem 3.5. Hence, ![]() $(T_1,T_2,T_3)$ belongs to
$(T_1,T_2,T_3)$ belongs to ![]() $\mathscr{S}^3(\mathbb{C}^3)$. Note that
$\mathscr{S}^3(\mathbb{C}^3)$. Note that
 \begin{equation*}
I-T_1T_1^*-T_2T_2^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I=\begin{bmatrix}
0&0\\
0&-2
\end{bmatrix} \ngeq 0.
\end{equation*}
\begin{equation*}
I-T_1T_1^*-T_2T_2^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I=\begin{bmatrix}
0&0\\
0&-2
\end{bmatrix} \ngeq 0.
\end{equation*}Also,
 \begin{equation*}
I-T_2T_2^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I= \begin{bmatrix}
0&0\\
0&-1
\end{bmatrix} \ngeq 0
\end{equation*}
\begin{equation*}
I-T_2T_2^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I= \begin{bmatrix}
0&0\\
0&-1
\end{bmatrix} \ngeq 0
\end{equation*}and
 \begin{equation*}
I-T_1T_1^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I= \begin{bmatrix}
0&0\\
0&-1
\end{bmatrix} \ngeq 0.
\end{equation*}
\begin{equation*}
I-T_1T_1^*-T_3T_3^*=I-\begin{bmatrix}
0&0\\
0&1
\end{bmatrix}-I= \begin{bmatrix}
0&0\\
0&-1
\end{bmatrix} \ngeq 0.
\end{equation*} Thus, if we consider  $\widehat{T}_1=(T_2,T_3)$,
$\widehat{T}_1=(T_2,T_3)$,  $\widehat{T}_2=(T_1,T_3)$ and
$\widehat{T}_2=(T_1,T_3)$ and  $\widehat{T}_3=(T_1,T_2)$, then
$\widehat{T}_3=(T_1,T_2)$, then ![]() $\widehat{T}_1$,
$\widehat{T}_1$, ![]() $\widehat{T}_2$ do not belong to
$\widehat{T}_2$ do not belong to ![]() $\mathbb{S}_{2}(\mathscr{H})$. So, for any
$\mathbb{S}_{2}(\mathscr{H})$. So, for any ![]() $p,q$ satisfying
$p,q$ satisfying ![]() $1\leq p,q \leq 3$, we have that
$1\leq p,q \leq 3$, we have that ![]() $(T_1,T_2,T_3)\notin \mathscr{T}^n_{p,q}(\mathscr{H})$.
$(T_1,T_2,T_3)\notin \mathscr{T}^n_{p,q}(\mathscr{H})$.
Note that example 5.4 does not satisfy Brehmer’s condition. Recall that ![]() $\underline{T}=(T_1,\dots,T_n)$ satisfies Brehmer’s conditions if
$\underline{T}=(T_1,\dots,T_n)$ satisfies Brehmer’s conditions if
 \begin{equation*}
\sum_{F\subseteq G}(-1)^{|F|}\underline{T}_{F}^*\underline{T}_F\geq 0
\end{equation*}
\begin{equation*}
\sum_{F\subseteq G}(-1)^{|F|}\underline{T}_{F}^*\underline{T}_F\geq 0
\end{equation*} for all ![]() $G\subseteq\{1,\ldots n \}$. See (2.1) for the definition. For
$G\subseteq\{1,\ldots n \}$. See (2.1) for the definition. For ![]() $\gamma=(\gamma_1,\ldots,\gamma_n)\in \mathbb{N}^n$, Curto and Vasilescu [Reference Curto and Vasilescu27, Reference Curto and Vasilescu28] introduced a notion of γ contractivity. For
$\gamma=(\gamma_1,\ldots,\gamma_n)\in \mathbb{N}^n$, Curto and Vasilescu [Reference Curto and Vasilescu27, Reference Curto and Vasilescu28] introduced a notion of γ contractivity. For ![]() $\gamma=(1,\ldots,1):=e$, the notion agrees with Brehmer’s condition. The notion of γ contractivity is defined in such a way that for each
$\gamma=(1,\ldots,1):=e$, the notion agrees with Brehmer’s condition. The notion of γ contractivity is defined in such a way that for each ![]() $\gamma \in \mathbb N^n$, if an operator
$\gamma \in \mathbb N^n$, if an operator ![]() $T=(T_1,\ldots,T_n)$ is γ contractive, then it is e contractive. Since example 5.4 does not satisfy Brehmer’s condition, it does not have a regular unitary dilation, and it is not e contractive. Hence, it cannot be γ contractive, and consequently, it does not belong to the ‘Curto–Vasilescu’ class.
$T=(T_1,\ldots,T_n)$ is γ contractive, then it is e contractive. Since example 5.4 does not satisfy Brehmer’s condition, it does not have a regular unitary dilation, and it is not e contractive. Hence, it cannot be γ contractive, and consequently, it does not belong to the ‘Curto–Vasilescu’ class.
Example 5.5. As observed by Barik, Das, Haria, and Sarkar in [Reference Barik, Das, Haria and Sarkar15], there is an operator tuple ![]() $(M_{z_1},\ldots,M_{z_n})$ in
$(M_{z_1},\ldots,M_{z_n})$ in  $\mathscr{T}^n_{p,q}(H^2(\mathbb{D}^n))$ that does not belong to
$\mathscr{T}^n_{p,q}(H^2(\mathbb{D}^n))$ that does not belong to  $\mathscr{P}^n_{p,q}(H^2(\mathbb{D}^n))$. This class was introduced in [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] by Grinshpan et al. Since
$\mathscr{P}^n_{p,q}(H^2(\mathbb{D}^n))$. This class was introduced in [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman36] by Grinshpan et al. Since ![]() $T=M_{z_1}\ldots M_{z_n}$ on
$T=M_{z_1}\ldots M_{z_n}$ on ![]() $H^2(\mathbb{D}^n)$ is an isometry,
$H^2(\mathbb{D}^n)$ is an isometry, ![]() $\mathscr{D}_{T}=0$. So the minimal isometric dilation space of T is
$\mathscr{D}_{T}=0$. So the minimal isometric dilation space of T is ![]() $\mathscr{K}_0=H^2(\mathbb{D}^n)$. Since each
$\mathscr{K}_0=H^2(\mathbb{D}^n)$. Since each ![]() $M_{z_i}=T_i$ is an isometry on
$M_{z_i}=T_i$ is an isometry on ![]() $H^2(\mathbb{D}^n)$, we have that
$H^2(\mathbb{D}^n)$, we have that ![]() $(M_{z_1},\ldots,M_{z_n})$ is an isometric dilation of
$(M_{z_1},\ldots,M_{z_n})$ is an isometric dilation of ![]() $(T_1,\ldots,T_n)$ on the minimal dilation space of T with the product being the minimal isometric dilation of T. Thus,
$(T_1,\ldots,T_n)$ on the minimal dilation space of T with the product being the minimal isometric dilation of T. Thus, ![]() $(M_{z_1},\ldots,M_{z_n})\in \mathscr{U}^n(\mathscr{H})$ by Theorem 3.5.
$(M_{z_1},\ldots,M_{z_n})\in \mathscr{U}^n(\mathscr{H})$ by Theorem 3.5.
Example 5.6. Let us consider the following commuting self-adjoint scalar matrices acting on ![]() $\mathbb{C}^3$:
$\mathbb{C}^3$:
 \begin{equation*}
T_1=\begin{bmatrix}
0&0&0\\
0&1&0\\
0&0&1
\end{bmatrix}, \;
T_2=\begin{bmatrix}
1&0&0\\
0&0&0\\
0&0&1
\end{bmatrix}, \;
T_3=\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&0
\end{bmatrix}.
\end{equation*}
\begin{equation*}
T_1=\begin{bmatrix}
0&0&0\\
0&1&0\\
0&0&1
\end{bmatrix}, \;
T_2=\begin{bmatrix}
1&0&0\\
0&0&0\\
0&0&1
\end{bmatrix}, \;
T_3=\begin{bmatrix}
1&0&0\\
0&1&0\\
0&0&0
\end{bmatrix}.
\end{equation*} Let ![]() $P_i=I-T_i$ and
$P_i=I-T_i$ and ![]() $U_i=I$ for
$U_i=I$ for ![]() $i=1,2,3$. Note that
$i=1,2,3$. Note that ![]() $D_T=0$ and the projections
$D_T=0$ and the projections ![]() $P_1,P_2,P_3$ satisfy
$P_1,P_2,P_3$ satisfy ![]() $P_1+P_2+P_3=I$. Thus, the condition (5) holds. Also, it can be easily verified that the conditions (1)–(4) hold. Therefore, this triple of commuting contractions belongs to
$P_1+P_2+P_3=I$. Thus, the condition (5) holds. Also, it can be easily verified that the conditions (1)–(4) hold. Therefore, this triple of commuting contractions belongs to ![]() $\mathscr{S}^3(\mathbb{C}^3)$.
$\mathscr{S}^3(\mathbb{C}^3)$.
Example 5.7. Let us consider the commuting self-adjoint scalar matrices
 \begin{equation*}
T_1=\begin{bmatrix}
0&1/3&0\\
1/3&0&0\\
0&0&0
\end{bmatrix}, \; T_2=\begin{bmatrix}
1/2&1/3&0\\
-1/3&1/2&0\\
0&0&0
\end{bmatrix}, \; T_3=\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1
\end{bmatrix}
\end{equation*}
\begin{equation*}
T_1=\begin{bmatrix}
0&1/3&0\\
1/3&0&0\\
0&0&0
\end{bmatrix}, \; T_2=\begin{bmatrix}
1/2&1/3&0\\
-1/3&1/2&0\\
0&0&0
\end{bmatrix}, \; T_3=\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1
\end{bmatrix}
\end{equation*} acting on ![]() $\mathbb{C}^3$. Evidently,
$\mathbb{C}^3$. Evidently, ![]() $T=T_1T_2T_3=0$, and thus,
$T=T_1T_2T_3=0$, and thus, ![]() $D_T=I$. Now suppose there are projections
$D_T=I$. Now suppose there are projections ![]() $P_1,P_2,P_3$ and commuting unitaries
$P_1,P_2,P_3$ and commuting unitaries ![]() $U_1,U_2,U_3$ satisfying conditions (1)–(4) of Theorem 3.5. So, in particular, we have
$U_1,U_2,U_3$ satisfying conditions (1)–(4) of Theorem 3.5. So, in particular, we have
which implies that ![]() $T_1=P_1^{\perp}U_1^*$. We also have
$T_1=P_1^{\perp}U_1^*$. We also have ![]() $D_TU_1P_1U_1^*D_T=I-T_1^*T_1$, and this gives
$D_TU_1P_1U_1^*D_T=I-T_1^*T_1$, and this gives ![]() $P_1=U_1^*(I-T_1^*T_1)U_1$, and hence, we have
$P_1=U_1^*(I-T_1^*T_1)U_1$, and hence, we have
 \begin{equation*}
P_1^{\perp}=I-U_1^*(I-T_1^*T_1)U_1=U_1^*T_1^*T_1U_1=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}U_1.
\end{equation*}
\begin{equation*}
P_1^{\perp}=I-U_1^*(I-T_1^*T_1)U_1=U_1^*T_1^*T_1U_1=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}U_1.
\end{equation*}Therefore,
 \begin{equation*}T_1=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}.
\end{equation*}
\begin{equation*}T_1=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}.
\end{equation*}Again
 \begin{equation*}
\begin{bmatrix}
3\\0\\0
\end{bmatrix}=T_1\begin{bmatrix}
0\\9\\0
\end{bmatrix}=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}\begin{bmatrix}
0\\9\\0
\end{bmatrix}=U_1^*\begin{bmatrix}
0\\1\\0
\end{bmatrix}.
\end{equation*}
\begin{equation*}
\begin{bmatrix}
3\\0\\0
\end{bmatrix}=T_1\begin{bmatrix}
0\\9\\0
\end{bmatrix}=U_1^*\begin{bmatrix}
1/9&0&0\\0&1/9&0\\0&0&0
\end{bmatrix}\begin{bmatrix}
0\\9\\0
\end{bmatrix}=U_1^*\begin{bmatrix}
0\\1\\0
\end{bmatrix}.
\end{equation*} This contradicts the fact that U 1 is a unitary. Hence, ![]() $(T_1,T_2,T_3)\notin \mathscr{U}^3(\mathbb{C}^3)$.
$(T_1,T_2,T_3)\notin \mathscr{U}^3(\mathbb{C}^3)$.
Example 5.8. Let ![]() $T_1,T_2$ be as in example 3.8 and let
$T_1,T_2$ be as in example 3.8 and let ![]() $T_3=I$. Then, it is evident that
$T_3=I$. Then, it is evident that ![]() $(T_1,T_2,T_3)$ does not belong to our class
$(T_1,T_2,T_3)$ does not belong to our class ![]() $\mathscr{S}^3(\mathbb{C}^3)$. This can be verified using an argument similar to that in example 5.7. However,
$\mathscr{S}^3(\mathbb{C}^3)$. This can be verified using an argument similar to that in example 5.7. However,
 \begin{equation*}
I-T_2T_2^*-T_3T_3^*+T_2T_3T_2^*T_3^*=I-\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}-I+\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}=0.
\end{equation*}
\begin{equation*}
I-T_2T_2^*-T_3T_3^*+T_2T_3T_2^*T_3^*=I-\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}-I+\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}=0.
\end{equation*}Alo,
 \begin{align*}
I-T_1T_1^*-T_2T_2^*+T_1T_2T_1^*T_2^*& =I-\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}-\begin{bmatrix}
0&0&0\\
0&1/9&0\\
0&0&1/27
\end{bmatrix}+0\\
& =\begin{bmatrix}
1&0&0\\
0&8/9&0\\
0&0&17/27
\end{bmatrix}\geq 0.
\end{align*}
\begin{align*}
I-T_1T_1^*-T_2T_2^*+T_1T_2T_1^*T_2^*& =I-\begin{bmatrix}
0&0&0\\
0&0&0\\
0&0&1/3
\end{bmatrix}-\begin{bmatrix}
0&0&0\\
0&1/9&0\\
0&0&1/27
\end{bmatrix}+0\\
& =\begin{bmatrix}
1&0&0\\
0&8/9&0\\
0&0&17/27
\end{bmatrix}\geq 0.
\end{align*} Hence, ![]() $\widehat{T}_1$ and
$\widehat{T}_1$ and ![]() $\widehat{T}_3$ belong to
$\widehat{T}_3$ belong to ![]() $\mathbb{S}_3(\mathbb{C}^3)$. Clearly
$\mathbb{S}_3(\mathbb{C}^3)$. Clearly ![]() $T_1,T_2$ are pure contractions, and hence,
$T_1,T_2$ are pure contractions, and hence, ![]() $\widehat{T}_3$ is pure. Thus,
$\widehat{T}_3$ is pure. Thus,  $(T_1,T_2,T_3)\in \mathscr{T}^3_{1,3}(\mathbb{C}^3)$.
$(T_1,T_2,T_3)\in \mathscr{T}^3_{1,3}(\mathbb{C}^3)$.
We now consider a few examples of contractions acting on infinite dimensional Hilbert spaces and study their dilations.
Example 5.9. Let ![]() $\mathscr{H}=l^2$ and let
$\mathscr{H}=l^2$ and let ![]() $T_1,T_2$ be the following weighted shift operators acting on
$T_1,T_2$ be the following weighted shift operators acting on ![]() $\mathscr{H}$:
$\mathscr{H}$:
where ![]() $\{a_0,a_1,\dots\}$ and
$\{a_0,a_1,\dots\}$ and ![]() $\{b_0,b_1,\dots \}$ are bounded sequences of non-zero real numbers with
$\{b_0,b_1,\dots \}$ are bounded sequences of non-zero real numbers with ![]() $|a_n| \lt 1$ and
$|a_n| \lt 1$ and ![]() $|b_n| \lt 1$ for every
$|b_n| \lt 1$ for every ![]() $n\in \mathbb N$. Clearly,
$n\in \mathbb N$. Clearly, ![]() $T=T_1T_2=T_2T_1=0$. Hence,
$T=T_1T_2=T_2T_1=0$. Hence, ![]() $D_T=I$ and
$D_T=I$ and ![]() $\mathscr{D}_T=l^2=\mathscr{H}$. We show that
$\mathscr{D}_T=l^2=\mathscr{H}$. We show that ![]() $(T_1,T_2)$ does not possess isometric dilation
$(T_1,T_2)$ does not possess isometric dilation ![]() $(V_1,V_2)$ on the minimal isometric dilation space of T with
$(V_1,V_2)$ on the minimal isometric dilation space of T with ![]() $V=V_1V_2 $ being the minimal isometric dilation of T. Let us assume the contrary. Then, by Theorem 3.5, there are projections
$V=V_1V_2 $ being the minimal isometric dilation of T. Let us assume the contrary. Then, by Theorem 3.5, there are projections ![]() $P_1,P_2$ commuting unitaries
$P_1,P_2$ commuting unitaries ![]() $U_1,U_2$ in
$U_1,U_2$ in ![]() $\mathscr{B}(\mathscr{D}_T)=\mathscr{B}(\mathscr{H})$, with
$\mathscr{B}(\mathscr{D}_T)=\mathscr{B}(\mathscr{H})$, with ![]() $U_1U_2=I$ satisfying conditions (1)–(5). Condition (1) gives us
$U_1U_2=I$ satisfying conditions (1)–(5). Condition (1) gives us ![]() $T_i=P_i^{\perp}U_i^*$ for
$T_i=P_i^{\perp}U_i^*$ for ![]() $i=1,2$. From condition (4), we have
$i=1,2$. From condition (4), we have
 \begin{align*}
U_1P_1U_1^*& =I-T_1^*T_1\\
\implies T_1^*T_1& =U_1(I-P_1)U_1^*\\
\implies T_1^*T_1& =U_1T_1 \kern5mm [\text{as } T_1=P_1^{\perp}U_1^* ].
\end{align*}
\begin{align*}
U_1P_1U_1^*& =I-T_1^*T_1\\
\implies T_1^*T_1& =U_1(I-P_1)U_1^*\\
\implies T_1^*T_1& =U_1T_1 \kern5mm [\text{as } T_1=P_1^{\perp}U_1^* ].
\end{align*} Simple calculation shows that ![]() $T_1^*T_1=diag(a_0^2,0,a_1^2,0,a_2^2,\dots)$. Hence,
$T_1^*T_1=diag(a_0^2,0,a_1^2,0,a_2^2,\dots)$. Hence,
 \begin{align*}
U_1T_1(a_0^{-1},0,\dots)& =T_1^*T_1(a_0^{-1},0,\dots)\\
\implies U_1(0,1,0,0,\dots)& =(a_0,0,0,\dots).
\end{align*}
\begin{align*}
U_1T_1(a_0^{-1},0,\dots)& =T_1^*T_1(a_0^{-1},0,\dots)\\
\implies U_1(0,1,0,0,\dots)& =(a_0,0,0,\dots).
\end{align*} Since U 1 is a unitary, ![]() $\|U_1(0,1,0,0,\dots)\|=\|(0,1,0,0,\dots)\| $, and thus, it follows from here that
$\|U_1(0,1,0,0,\dots)\|=\|(0,1,0,0,\dots)\| $, and thus, it follows from here that ![]() $\| (a_0,0,0,\dots)\|=\|(0,1,0,0,\dots) \|$. This is a contradiction as
$\| (a_0,0,0,\dots)\|=\|(0,1,0,0,\dots) \|$. This is a contradiction as ![]() $|a_0| \lt 1$. Hence, we are done.
$|a_0| \lt 1$. Hence, we are done.
Example 5.10. Let ![]() $\mathscr{H}=l^2$ and let
$\mathscr{H}=l^2$ and let ![]() $\{e_0,e_1,\dots \}$ be the standard orthonormal basis of l 2. For
$\{e_0,e_1,\dots \}$ be the standard orthonormal basis of l 2. For ![]() $k=1,\dots,n $, let Tk be defined on
$k=1,\dots,n $, let Tk be defined on ![]() $\mathscr{H}$ by
$\mathscr{H}$ by ![]() $T_k(e_m)=0 $ if
$T_k(e_m)=0 $ if ![]() $ m\equiv (k-1)mod \,n$ and
$ m\equiv (k-1)mod \,n$ and ![]() $T_k(e_m)=e_m$ otherwise. We show that
$T_k(e_m)=e_m$ otherwise. We show that ![]() $(T_1,T_2,\dots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space
$(T_1,T_2,\dots,T_n)$ possesses an isometric dilation on the minimal isometric dilation space ![]() $\mathscr{K}$ of
$\mathscr{K}$ of ![]() $T=\prod_{i=1}^nT_i$. Evidently, T = 0, and thus,
$T=\prod_{i=1}^nT_i$. Evidently, T = 0, and thus, ![]() $\mathscr{D}_T= \mathscr{H}$. So, we have that
$\mathscr{D}_T= \mathscr{H}$. So, we have that ![]() $\mathscr{K}=\mathscr{H}\oplus \mathscr{H}\oplus \dots$ is the minimal isometric dilation space of T. Now for each k, define
$\mathscr{K}=\mathscr{H}\oplus \mathscr{H}\oplus \dots$ is the minimal isometric dilation space of T. Now for each k, define ![]() $P_k=I-T_k$ and
$P_k=I-T_k$ and ![]() $U_k=I $ on
$U_k=I $ on ![]() $\mathscr{D}_T= \mathscr{H}$. Then, it follows that
$\mathscr{D}_T= \mathscr{H}$. Then, it follows that ![]() $U_1,\dots,U_n$ are commuting unitaries with
$U_1,\dots,U_n$ are commuting unitaries with ![]() $ U_1U_2\dots U_n=I$ and
$ U_1U_2\dots U_n=I$ and ![]() $P_1,\dots,P_n$ are projections. Also, the conditions (1)–(5) of Theorem 3.5 are satisfied straightway. Therefore, Theorem 3.5 guaranties the existence of an isometric dilation of
$P_1,\dots,P_n$ are projections. Also, the conditions (1)–(5) of Theorem 3.5 are satisfied straightway. Therefore, Theorem 3.5 guaranties the existence of an isometric dilation of ![]() $(T_1, \dots, T_n)$ as desired.
$(T_1, \dots, T_n)$ as desired.
6. Sz. Nagy–Foias-type isometric dilation and functional model
Recall that a c.n.u. contraction T on a Hilbert space ![]() $\mathscr{H}$ is a contraction such that there is no non-zero subspace
$\mathscr{H}$ is a contraction such that there is no non-zero subspace ![]() $\mathscr{H}_1$ of
$\mathscr{H}_1$ of ![]() $\mathscr{H}$ that reduces T and on
$\mathscr{H}$ that reduces T and on ![]() ${\mathscr{H}_1}$ the operator T acts as a unitary. In simple words, a c.n.u. contraction is a contraction without any unitary part. Let T on
${\mathscr{H}_1}$ the operator T acts as a unitary. In simple words, a c.n.u. contraction is a contraction without any unitary part. Let T on ![]() $\mathscr{H}$ be a c.n.u. contraction and let V on
$\mathscr{H}$ be a c.n.u. contraction and let V on ![]() $\mathscr{K}_{0}$ be the minimal isometric dilation of T. By Wold decomposition,
$\mathscr{K}_{0}$ be the minimal isometric dilation of T. By Wold decomposition, ![]() $\mathscr{K}_0$ splits into reducing subspaces
$\mathscr{K}_0$ splits into reducing subspaces ![]() $\mathscr{K}_{01}$,
$\mathscr{K}_{01}$, ![]() $\mathscr{K}_{02}$ of V such that
$\mathscr{K}_{02}$ of V such that ![]() $\mathscr{K}_0=\mathscr{K}_{01}\oplus \mathscr{K}_{02}$ and that
$\mathscr{K}_0=\mathscr{K}_{01}\oplus \mathscr{K}_{02}$ and that ![]() $V|_{\mathscr{K}_{01}}$ is unitarily equivalent to a unilateral shift and
$V|_{\mathscr{K}_{01}}$ is unitarily equivalent to a unilateral shift and ![]() $V|_{\mathscr{K}_{02}}$ is a unitary. Then,
$V|_{\mathscr{K}_{02}}$ is a unitary. Then, ![]() $\mathscr{K}_{01}$ can be identified with
$\mathscr{K}_{01}$ can be identified with ![]() $H^2(\mathscr{D}_{T^*})$ and
$H^2(\mathscr{D}_{T^*})$ and ![]() $\mathscr{K}_{02}$ can be identified with
$\mathscr{K}_{02}$ can be identified with  $\overline{\Delta_{T}(L^2(\mathscr{D}_T))}$, where
$\overline{\Delta_{T}(L^2(\mathscr{D}_T))}$, where  $\Delta_{T}(t)=[I_{\mathscr{D}_T}-\Theta_T(e^{it})^*\Theta_T(e^{it})]^{1/2}$ and
$\Delta_{T}(t)=[I_{\mathscr{D}_T}-\Theta_T(e^{it})^*\Theta_T(e^{it})]^{1/2}$ and ![]() $\Theta_T$ being the characteristic function of the contraction T. For further details, see chapter VI of [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]. Thus,
$\Theta_T$ being the characteristic function of the contraction T. For further details, see chapter VI of [Reference Bercovici, Foias, Kerchy and Sz.-Nagy17]. Thus, ![]() $\mathscr{K}_{0}= \mathscr{K}_{01}\oplus \mathscr{K}_{02}$ can be identified with
$\mathscr{K}_{0}= \mathscr{K}_{01}\oplus \mathscr{K}_{02}$ can be identified with ![]() $\mathbb{K}_{+}=H^2(\mathscr{D}_{T^*})\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}$. Also, the isometry V on
$\mathbb{K}_{+}=H^2(\mathscr{D}_{T^*})\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}$. Also, the isometry V on ![]() $\mathscr{K}_0$ can be realized as
$\mathscr{K}_0$ can be realized as  $M_z \oplus M_{e^{it}}|_{\overline{\Delta_T(L^2(\mathscr{D}_T))}}$. Therefore, there is a unitary
$M_z \oplus M_{e^{it}}|_{\overline{\Delta_T(L^2(\mathscr{D}_T))}}$. Therefore, there is a unitary
 \begin{equation}
\tau=\tau_1\oplus \tau_2:\mathscr{K}_{01}\oplus \mathscr{K}_{02}\to (H^2\otimes \mathscr{D}_{T^*})\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}\, :=\widetilde{\mathbb{K}}_{+}
\end{equation}
\begin{equation}
\tau=\tau_1\oplus \tau_2:\mathscr{K}_{01}\oplus \mathscr{K}_{02}\to (H^2\otimes \mathscr{D}_{T^*})\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}\, :=\widetilde{\mathbb{K}}_{+}
\end{equation} such that V on ![]() $\mathscr{K}_0$ can be realized as
$\mathscr{K}_0$ can be realized as  $(M_z \otimes I_{\mathscr{D}_{T^*}}) \oplus M_{e^{it}}|_{\overline{\Delta_T(L^2(\mathscr{D}_T))}}$ on
$(M_z \otimes I_{\mathscr{D}_{T^*}}) \oplus M_{e^{it}}|_{\overline{\Delta_T(L^2(\mathscr{D}_T))}}$ on  $\widetilde{\mathbb{K}}_{+}$.
$\widetilde{\mathbb{K}}_{+}$.
If ![]() $(T_1,\ldots,T_n)$ is a tuple of commuting contractions acting on
$(T_1,\ldots,T_n)$ is a tuple of commuting contractions acting on ![]() $\mathscr{H}$ satisfying the hypotheses of Theorem 3.9, then it possesses an isometric dilation
$\mathscr{H}$ satisfying the hypotheses of Theorem 3.9, then it possesses an isometric dilation ![]() $(V_1,\ldots,V_n)$ on the minimal isometric dilation space
$(V_1,\ldots,V_n)$ on the minimal isometric dilation space ![]() $\mathscr{K}_0$ of T. By Wold decomposition of commuting isometries, we have that
$\mathscr{K}_0$ of T. By Wold decomposition of commuting isometries, we have that ![]() $\mathscr{K}_{01}$ and
$\mathscr{K}_{01}$ and ![]() $\mathscr{K}_{02}$ are reducing subspaces for each Vi and that
$\mathscr{K}_{02}$ are reducing subspaces for each Vi and that
is a unitary for ![]() $1\leq i \leq n$. Now we state our dilation theorem and functional model in the Sz. Nagy–Foias setting. This is another main result of this article.
$1\leq i \leq n$. Now we state our dilation theorem and functional model in the Sz. Nagy–Foias setting. This is another main result of this article.
Theorem 6.1 Let ![]() $(T_1,\ldots,T_n)$ be a tuple of commuting contractions acting on
$(T_1,\ldots,T_n)$ be a tuple of commuting contractions acting on ![]() $\mathscr{H}$ such that
$\mathscr{H}$ such that ![]() $T=\Pi_{i=1}^nT_i$ is a c.n.u. contraction. Suppose there are orthogonal projections
$T=\Pi_{i=1}^nT_i$ is a c.n.u. contraction. Suppose there are orthogonal projections ![]() $P_1,\ldots,P_n$ and commuting unitaries
$P_1,\ldots,P_n$ and commuting unitaries ![]() $U_1,\ldots,U_n $ in
$U_1,\ldots,U_n $ in ![]() $\mathscr{B}(\mathscr{D}_T)$ satisfying
$\mathscr{B}(\mathscr{D}_T)$ satisfying
(1)
 $D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,
$D_TT_i=P_i^{\perp}U_i^*D_T+P_iU_i^*D_TT$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_TU_iP_iU_i^*D_T=D_{T_i}^2$
$D_TU_iP_iU_i^*D_T=D_{T_i}^2$
for ![]() $1\leq i \lt j\leq n$. Then, there are projections
$1\leq i \lt j\leq n$. Then, there are projections ![]() $Q_1,\ldots,Q_n$ and commuting unitaries
$Q_1,\ldots,Q_n$ and commuting unitaries ![]() $\widetilde{U}_1,\ldots,\widetilde{U}_n$ in
$\widetilde{U}_1,\ldots,\widetilde{U}_n$ in ![]() $\mathscr{B}(\mathscr{D}_{T^*})$ such that
$\mathscr{B}(\mathscr{D}_{T^*})$ such that ![]() $(T_1, \dots, T_n)$ dilates to the tuple of commuting isometries
$(T_1, \dots, T_n)$ dilates to the tuple of commuting isometries  $(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots,\widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ on
$(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots,\widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ on  $\widetilde{\mathbb{K}}_+=H^2\otimes \mathscr{D}_{T^*}\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}$, where
$\widetilde{\mathbb{K}}_+=H^2\otimes \mathscr{D}_{T^*}\oplus \overline{\Delta_{T}(L^2(\mathscr{D}_T))}$, where
 \begin{align*}
\widetilde{V}_{i1}&=I\otimes\widetilde{U}_iQ_i^{\perp}+M_z\otimes \widetilde{U}_iQ_i\,,\\
\widetilde{V}_{i2}&=\tau_2V_{i2}\tau_2^* \,,
\end{align*}
\begin{align*}
\widetilde{V}_{i1}&=I\otimes\widetilde{U}_iQ_i^{\perp}+M_z\otimes \widetilde{U}_iQ_i\,,\\
\widetilde{V}_{i2}&=\tau_2V_{i2}\tau_2^* \,,
\end{align*} for unitaries τ 2 and ![]() $V_{i2}$ as in (6.1) and (6.2), respectively, for
$V_{i2}$ as in (6.1) and (6.2), respectively, for ![]() $1 \leq i \leq n$.
$1 \leq i \leq n$.
Proof. By Theorem 3.9, we have that ![]() $(T_1,\ldots,T_n)$ possesses an isometric dilation
$(T_1,\ldots,T_n)$ possesses an isometric dilation ![]() $(V_1,\ldots,V_n)$ on
$(V_1,\ldots,V_n)$ on ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T})$, which in fact satisfies
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T})$, which in fact satisfies ![]() $V_i^*|_{\mathscr{H}}=T_i^*$ for
$V_i^*|_{\mathscr{H}}=T_i^*$ for ![]() $1\leq i \leq n$. Now
$1\leq i \leq n$. Now ![]() $\mathscr{K}_0$ has an orthogonal decomposition
$\mathscr{K}_0$ has an orthogonal decomposition ![]() $\mathscr{K}_0=\mathscr{K}_{01}\oplus \mathscr{K}_{02}$ such that
$\mathscr{K}_0=\mathscr{K}_{01}\oplus \mathscr{K}_{02}$ such that ![]() $\mathscr{K}_{01}$ and
$\mathscr{K}_{01}$ and ![]() $\mathscr{K}_{02}$ are common reducing subspaces for
$\mathscr{K}_{02}$ are common reducing subspaces for ![]() $V_1,\ldots,V_n$,
$V_1,\ldots,V_n$, ![]() $(V_1|_{\mathscr{K}_{01}},\ldots,V_n|_{\mathscr{K}_{01}})$ is a pure isometric tuple, i.e.,
$(V_1|_{\mathscr{K}_{01}},\ldots,V_n|_{\mathscr{K}_{01}})$ is a pure isometric tuple, i.e., ![]() $\prod_{i=}^n V_i|_{\mathscr{K}_{01}}$ is a pure isometry and
$\prod_{i=}^n V_i|_{\mathscr{K}_{01}}$ is a pure isometry and ![]() $(V_1|_{\mathscr{K}_{02}},\ldots,V_n|_{\mathscr{K}_{02}})$ is a unitary tuple. Let
$(V_1|_{\mathscr{K}_{02}},\ldots,V_n|_{\mathscr{K}_{02}})$ is a unitary tuple. Let ![]() $ \prod_{i=1}^nV_i=V$,
$ \prod_{i=1}^nV_i=V$, ![]() $V_i|_{\mathscr{K}_{01}}=V_{i1}$, and
$V_i|_{\mathscr{K}_{01}}=V_{i1}$, and ![]() $V_i|_{\mathscr{K}_{02}}=V_{i2}$ for
$V_i|_{\mathscr{K}_{02}}=V_{i2}$ for ![]() $1\leq i \leq n$. Also, let
$1\leq i \leq n$. Also, let ![]() $ \prod_{i=1}^nV_{i1}=W_1$ and
$ \prod_{i=1}^nV_{i1}=W_1$ and ![]() $ \prod_{i=1}^nV_{i2}=W_2 $. So W 1 on
$ \prod_{i=1}^nV_{i2}=W_2 $. So W 1 on ![]() $\mathscr{K}_{01}$ is a pure isometry and W 2 on
$\mathscr{K}_{01}$ is a pure isometry and W 2 on ![]() $\mathscr{K}_{02}$ is a unitary. So,
$\mathscr{K}_{02}$ is a unitary. So,
is an isometric dilation of ![]() $(T_1,\ldots, T_n)$ on
$(T_1,\ldots, T_n)$ on  $\widetilde{\mathbb{K}}_+$, where
$\widetilde{\mathbb{K}}_+$, where ![]() $\tau=\tau_1\oplus \tau_2$ is as in (6.1). Thus, the tuple
$\tau=\tau_1\oplus \tau_2$ is as in (6.1). Thus, the tuple ![]() $(\tau_1 V_{11} \tau_1^*,\ldots \tau_1 V_{n1} \tau_1^*)$ on
$(\tau_1 V_{11} \tau_1^*,\ldots \tau_1 V_{n1} \tau_1^*)$ on ![]() $H^2\otimes \mathscr{D}_{T^*}$ is a pure isometric tuple. Hence, by Theorem 3.1, there exist commuting unitaries
$H^2\otimes \mathscr{D}_{T^*}$ is a pure isometric tuple. Hence, by Theorem 3.1, there exist commuting unitaries ![]() $\widetilde{U}_1,\ldots, \widetilde{U}_n$ and orthogonal projections
$\widetilde{U}_1,\ldots, \widetilde{U}_n$ and orthogonal projections ![]() $Q_1,\ldots,Q_n$ in
$Q_1,\ldots,Q_n$ in  $\mathscr{B}(\mathscr{D}_{T^*}) \; (=\mathscr{B}(D_{W_1^*}))$ such that the tuple
$\mathscr{B}(\mathscr{D}_{T^*}) \; (=\mathscr{B}(D_{W_1^*}))$ such that the tuple ![]() $(\tau_1 V_{11} \tau_1^*,\ldots \tau_1 V_{n1} \tau_1^*)$ is unitarily equivalent to
$(\tau_1 V_{11} \tau_1^*,\ldots \tau_1 V_{n1} \tau_1^*)$ is unitarily equivalent to
 \begin{equation*}
(I\otimes \widetilde{U}_1Q_1^{\perp}+M_z \otimes \widetilde{U}_1Q_1,\ldots,I\otimes \widetilde{U}_nQ_n^{\perp}+M_z \otimes \widetilde{U}_nQ_n) \quad \text{on } \quad {H}^2\otimes \mathscr{D}_{T^*}
\end{equation*}
\begin{equation*}
(I\otimes \widetilde{U}_1Q_1^{\perp}+M_z \otimes \widetilde{U}_1Q_1,\ldots,I\otimes \widetilde{U}_nQ_n^{\perp}+M_z \otimes \widetilde{U}_nQ_n) \quad \text{on } \quad {H}^2\otimes \mathscr{D}_{T^*}
\end{equation*} via a unitary, say Z. For ![]() $1\leq i \leq n$, let us denote
$1\leq i \leq n$, let us denote  $\widetilde{V}_{i1}= I\otimes\widetilde{U}_iQ_i^{\perp}+M_z \otimes \widetilde{U}_iQ_i$ and
$\widetilde{V}_{i1}= I\otimes\widetilde{U}_iQ_i^{\perp}+M_z \otimes \widetilde{U}_iQ_i$ and  $\widetilde{V}_{i2}=\tau_2 V_{i2} \tau_2^* $. So,
$\widetilde{V}_{i2}=\tau_2 V_{i2} \tau_2^* $. So, ![]() $(\tau V_1 \tau^*,\ldots,\tau V_n \tau^*) $ is unitarily equivalent to
$(\tau V_1 \tau^*,\ldots,\tau V_n \tau^*) $ is unitarily equivalent to  $(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2}) $ via the unitary
$(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2}) $ via the unitary ![]() $Z\oplus I$. Thus,
$Z\oplus I$. Thus, ![]() $(V_1,\ldots,V_n)$ is unitarily equivalent to
$(V_1,\ldots,V_n)$ is unitarily equivalent to  $(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ via a unitary
$(\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ via a unitary
Let ![]() $\widetilde{V}_i=\widetilde{V}_{i1}\oplus \widetilde{V}_{i2}$ for
$\widetilde{V}_i=\widetilde{V}_{i1}\oplus \widetilde{V}_{i2}$ for ![]() $i=1,\ldots n$. Since for each i,
$i=1,\ldots n$. Since for each i, ![]() $V_i^*|_{\mathscr{H}}=T_i^*$, we have, for any
$V_i^*|_{\mathscr{H}}=T_i^*$, we have, for any ![]() $h\in \mathscr{H} $,
$h\in \mathscr{H} $,
 \begin{equation*}
\widetilde{V}_i^*(Yh)=(YV_iY^*)^*Yh=YV_i^*Y^*Yh=YV_i^*h=YT_i^*h.
\end{equation*}
\begin{equation*}
\widetilde{V}_i^*(Yh)=(YV_iY^*)^*Yh=YV_i^*Y^*Yh=YV_i^*h=YT_i^*h.
\end{equation*} Therefore,  $\widetilde{V}_i^*|_{Y(\mathscr{H})}=YT_i^*Y^*|_{Y(\mathscr{H})}$ for
$\widetilde{V}_i^*|_{Y(\mathscr{H})}=YT_i^*Y^*|_{Y(\mathscr{H})}$ for ![]() $1\leq i \leq n$. So, we have
$1\leq i \leq n$. So, we have  $T_1^{k_1}\ldots T_n^{k_n}=Y^*\widetilde{V}_1^{k_1}\ldots \widetilde{V}_n^{k_n}Y $. Thus,
$T_1^{k_1}\ldots T_n^{k_n}=Y^*\widetilde{V}_1^{k_1}\ldots \widetilde{V}_n^{k_n}Y $. Thus,  $ (\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ is an isometric dilation of
$ (\widetilde{V}_{11}\oplus \widetilde{V}_{12},\ldots, \widetilde{V}_{n1}\oplus \widetilde{V}_{n2})$ is an isometric dilation of ![]() $(T_1,\ldots, T_n ) $, where
$(T_1,\ldots, T_n ) $, where  $\widetilde{V}_{i1}= I\otimes\widetilde{U}_iQ_i^{\perp}+M_z \otimes \widetilde{U}_iQ_i$ and
$\widetilde{V}_{i1}= I\otimes\widetilde{U}_iQ_i^{\perp}+M_z \otimes \widetilde{U}_iQ_i$ and  $\widetilde{V}_{i2}=\tau_2 V_{i2} \tau_2^* $ for
$\widetilde{V}_{i2}=\tau_2 V_{i2} \tau_2^* $ for ![]() $1\leq i \leq n$. This completes the proof.
$1\leq i \leq n$. This completes the proof.
7. A model theory for a class of commuting contractions
In this section, we present a model theory for a tuple of commuting contractions satisfying the conditions of Theorems 3.5 and 3.9.
Theorem 7.1 Let ![]() $(T_1,\ldots, T_n)$ be commuting tuple of contractions on a Hilbert space
$(T_1,\ldots, T_n)$ be commuting tuple of contractions on a Hilbert space ![]() $\mathscr{H}$ and let
$\mathscr{H}$ and let ![]() $T=\Pi_{i=1}^nT_i$. Suppose there are projections
$T=\Pi_{i=1}^nT_i$. Suppose there are projections ![]() $P_1,\ldots,P_n\in \mathscr{B}(\mathscr{D}_{T^*})$ and commuting unitaries
$P_1,\ldots,P_n\in \mathscr{B}(\mathscr{D}_{T^*})$ and commuting unitaries ![]() $U_1,\ldots,U_n\in \mathscr{B}(\mathscr{D}_{T^*})$ such that for each
$U_1,\ldots,U_n\in \mathscr{B}(\mathscr{D}_{T^*})$ such that for each ![]() $i=1, \dots, n$,
$i=1, \dots, n$,
(1)
 $D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,
$D_{T^*}T_i^*=P_i^{\perp}U_i^*D_{T^*}+P_iU_i^*D_{T^*}T^*$,(2)
 $P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,
$P_i^{\perp}U_i^*P_j^{\perp}U_j^*=P_j^{\perp}U_j^*P_i^{\perp}U_i^*$,(3)
 $U_iP_iU_jP_j=U_jP_jU_iP_i$,
$U_iP_iU_jP_j=U_jP_jU_iP_i$,(4)
 $D_{T^*}U_iP_iU_i^*D_{T^*}=D_{T_i^*}^2$.
$D_{T^*}U_iP_iU_i^*D_{T^*}=D_{T_i^*}^2$.
Let ![]() $Z_1,\ldots,Z_n$ on
$Z_1,\ldots,Z_n$ on ![]() $\mathscr{K}=\mathscr{H}\oplus l^2(\mathscr{D}_{T^*})$ be defined as follows:
$\mathscr{K}=\mathscr{H}\oplus l^2(\mathscr{D}_{T^*})$ be defined as follows:
 \begin{equation*} Z_i=\begin{bmatrix}
T_i&D_{T^*}U_iP_i&0&0&\ldots \\
0&U_iP_i^{\perp}&U_iP_i&0&\ldots \\
0&0&U_iP_i^{\perp}&U_iP_i&\ldots \\
0&0&0&U_iP_i^{\perp}&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix} , \qquad (1\leq i \leq n).
\end{equation*}
\begin{equation*} Z_i=\begin{bmatrix}
T_i&D_{T^*}U_iP_i&0&0&\ldots \\
0&U_iP_i^{\perp}&U_iP_i&0&\ldots \\
0&0&U_iP_i^{\perp}&U_iP_i&\ldots \\
0&0&0&U_iP_i^{\perp}&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix} , \qquad (1\leq i \leq n).
\end{equation*}Then,
(i)
 $(Z_1,\ldots,Z_n)$ is a commuting n-tuple of co-isometries,
$(Z_1,\ldots,Z_n)$ is a commuting n-tuple of co-isometries,  $\mathscr{H}$ is a common invariant subspace of
$\mathscr{H}$ is a common invariant subspace of  $Z_1,\ldots,Z_n$, and
$Z_1,\ldots,Z_n$, and  $Z_i|_{\mathscr{H}}=T_i$.
$Z_i|_{\mathscr{H}}=T_i$.(ii) there is an orthogonal decomposition
 $\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$ into common reducing subspaces of
$\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$ into common reducing subspaces of  $Z_1,\ldots,Z_n$ such that
$Z_1,\ldots,Z_n$ such that  $(Z_1|_{\mathscr{K}_1},\ldots,Z_n|_{\mathscr{K}_1})$ is a pure co-isometric tuple, that is,
$(Z_1|_{\mathscr{K}_1},\ldots,Z_n|_{\mathscr{K}_1})$ is a pure co-isometric tuple, that is,  $Z|_{\mathscr{K}_1}=\Pi_{i=1}^nZ_i|_{\mathscr{K}_1}$ is a pure co-isometry and
$Z|_{\mathscr{K}_1}=\Pi_{i=1}^nZ_i|_{\mathscr{K}_1}$ is a pure co-isometry and  $(Z_1|_{\mathscr{K}_2},\ldots,Z_n|_{\mathscr{K}_2})$ is a unitary tuple.
$(Z_1|_{\mathscr{K}_2},\ldots,Z_n|_{\mathscr{K}_2})$ is a unitary tuple.
Additionally, if
then
(iii)
 $\mathscr{K}_1$ can be identified with
$\mathscr{K}_1$ can be identified with  $H^2(\mathscr{D}_{Z})$, where
$H^2(\mathscr{D}_{Z})$, where  $\mathscr{D}_Z$ has same dimension as that of
$\mathscr{D}_Z$ has same dimension as that of  $\mathscr{D}_T$. Also, there are projections
$\mathscr{D}_T$. Also, there are projections  $\widehat{P_1},\ldots,\widehat{P_n}$ and commuting unitaries
$\widehat{P_1},\ldots,\widehat{P_n}$ and commuting unitaries  $ \widehat{U_1},\ldots,\widehat{U_n}$ such that the operator tuple
$ \widehat{U_1},\ldots,\widehat{U_n}$ such that the operator tuple  $(Z_1|_{\mathscr{K}_1},\ldots, Z_n|_{\mathscr{K}_1})$ is unitarily equivalent to the multiplication operator tuple
$(Z_1|_{\mathscr{K}_1},\ldots, Z_n|_{\mathscr{K}_1})$ is unitarily equivalent to the multiplication operator tuple
 \begin{equation*}
\left( M_{\widehat{U_1}\widehat{P_1}^{\perp}+\widehat{U_1}\widehat{P_1}\bar{z}},\ldots,M_{\widehat{U_n}\widehat{P_n}^{\perp}+\widehat{U_n}\widehat{P_n}\bar{z}} \right)
\end{equation*}
\begin{equation*}
\left( M_{\widehat{U_1}\widehat{P_1}^{\perp}+\widehat{U_1}\widehat{P_1}\bar{z}},\ldots,M_{\widehat{U_n}\widehat{P_n}^{\perp}+\widehat{U_n}\widehat{P_n}\bar{z}} \right)
\end{equation*}acting on
 $H^2(\mathscr{D}_{T})$.
$H^2(\mathscr{D}_{T})$.
Proof. We apply Theorem 3.9 to the tuple ![]() $(T_1^*,\ldots,T_n^*)$ of commuting contractions to have an isometric dilation
$(T_1^*,\ldots,T_n^*)$ of commuting contractions to have an isometric dilation ![]() $(X_1,\ldots,X_n)$ on
$(X_1,\ldots,X_n)$ on ![]() $\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T^*})$, where
$\mathscr{K}_0=\mathscr{H}\oplus l^2(\mathscr{D}_{T^*})$, where
 \begin{equation*}
X_i=\begin{bmatrix}
T_i^*&0&0&0&\ldots \\
P_iU_i^*D_{T^*}&P_i^{\perp}U_i^*&0&0&\ldots \\
0&P_iU_i^*&P_i^{\perp}U_i^*&0&\ldots \\
0&0&P_iU_i^*&P_i^{\perp}U_i^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix} , \qquad (1\leq i \leq n).
\end{equation*}
\begin{equation*}
X_i=\begin{bmatrix}
T_i^*&0&0&0&\ldots \\
P_iU_i^*D_{T^*}&P_i^{\perp}U_i^*&0&0&\ldots \\
0&P_iU_i^*&P_i^{\perp}U_i^*&0&\ldots \\
0&0&P_iU_i^*&P_i^{\perp}U_i^*&\ldots \\
\ldots & \ldots & \ldots & \ldots & \ldots
\end{bmatrix} , \qquad (1\leq i \leq n).
\end{equation*} Clearly, ![]() $Z_i=X_i^*$ for each i, and it is evident from the block matrix that
$Z_i=X_i^*$ for each i, and it is evident from the block matrix that ![]() $\mathscr{H}$ is a common invariant subspace for each Zi and
$\mathscr{H}$ is a common invariant subspace for each Zi and ![]() $Z_i|_{\mathscr{H}}=T_i$. This proves (i). Since
$Z_i|_{\mathscr{H}}=T_i$. This proves (i). Since ![]() $(X_1,\ldots,X_n)$ is a commuting tuple of isometry,
$(X_1,\ldots,X_n)$ is a commuting tuple of isometry, ![]() $X=\Pi_{i=1}^nX_i$ is an isometry. By Wold decomposition,
$X=\Pi_{i=1}^nX_i$ is an isometry. By Wold decomposition, ![]() $\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$ and that
$\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$ and that ![]() $X|_{\mathscr{K}_1}$ is a pure isometry,
$X|_{\mathscr{K}_1}$ is a pure isometry, ![]() $X|_{\mathscr{K}_2}$ is a unitary. Also, they are common reducing subspaces for each Xi. Indeed, if
$X|_{\mathscr{K}_2}$ is a unitary. Also, they are common reducing subspaces for each Xi. Indeed, if
 \begin{equation*}
X_i=\begin{pmatrix}
A_i&B_i\\ C_i&D_i
\end{pmatrix} \quad \quad X=\begin{pmatrix}
X_{K1} & 0\\
0 & X_{K2}
\end{pmatrix}
\end{equation*}
\begin{equation*}
X_i=\begin{pmatrix}
A_i&B_i\\ C_i&D_i
\end{pmatrix} \quad \quad X=\begin{pmatrix}
X_{K1} & 0\\
0 & X_{K2}
\end{pmatrix}
\end{equation*} with respect to the decomposition ![]() $\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$, then
$\mathscr{K}=\mathscr{K}_1\oplus \mathscr{K}_2$, then ![]() $X_iX=XX_i$ implies that
$X_iX=XX_i$ implies that
Therefore, for all ![]() $k\in\mathbb{N}$, we have
$k\in\mathbb{N}$, we have
Now ![]() $X_{K1}$ is a pure isometry and
$X_{K1}$ is a pure isometry and ![]() $X_{K2}$ is unitary, so on the one hand, we have
$X_{K2}$ is unitary, so on the one hand, we have ![]() $\|X_{K2}^{*k}B_i^*\|= \|B_i^*\|$, and on the other hand,
$\|X_{K2}^{*k}B_i^*\|= \|B_i^*\|$, and on the other hand, ![]() $\|B_i^*X_{K1}^{*k}\|\to 0$ as
$\|B_i^*X_{K1}^{*k}\|\to 0$ as ![]() $k \rightarrow \infty $. Hence,
$k \rightarrow \infty $. Hence, ![]() $B_i=0$. Similarly,
$B_i=0$. Similarly, ![]() $C_i=0$ for
$C_i=0$ for ![]() $1\leq i \leq n$. Thus, with respect to the decomposition
$1\leq i \leq n$. Thus, with respect to the decomposition ![]() $\mathscr{K}=\mathscr{K}_1\oplus\mathscr{K}_2$, the operator Xi takes form
$\mathscr{K}=\mathscr{K}_1\oplus\mathscr{K}_2$, the operator Xi takes form
 \begin{equation*}
X_i= \begin{pmatrix}
X_{i1}&0\\
0&X_{i2}
\end{pmatrix}, \qquad (1\leq i \leq n).
\end{equation*}
\begin{equation*}
X_i= \begin{pmatrix}
X_{i1}&0\\
0&X_{i2}
\end{pmatrix}, \qquad (1\leq i \leq n).
\end{equation*} Now since Xi is an isometry, so will be ![]() $X_{i1}$,
$X_{i1}$, ![]() $X_{i1}'=\Pi_{j\neq i}X_{j1}$ and
$X_{i1}'=\Pi_{j\neq i}X_{j1}$ and ![]() $X_{i2}$,
$X_{i2}$, ![]() $X_{i2}'=\Pi_{j\neq i}X_{j2}$. Further from the block matrix of Xi and from the fact that
$X_{i2}'=\Pi_{j\neq i}X_{j2}$. Further from the block matrix of Xi and from the fact that ![]() $X=\Pi_{i=1}^nX_i$, it is clear that
$X=\Pi_{i=1}^nX_i$, it is clear that ![]() $X_{K2}=\Pi_{i=1}^nX_{i2}$. Again,
$X_{K2}=\Pi_{i=1}^nX_{i2}$. Again, ![]() $X_{K2}$ is a unitary,
$X_{K2}$ is a unitary, ![]() $X_{i2}'$ is an isometry, and
$X_{i2}'$ is an isometry, and ![]() $X_{i2'}^*X_{K2}=X_{i2}$. So, we have
$X_{i2'}^*X_{K2}=X_{i2}$. So, we have
Thus, ![]() $X_{i2}$ is a unitary on
$X_{i2}$ is a unitary on ![]() $\mathscr{K}_2$ for each
$\mathscr{K}_2$ for each ![]() $i=1,\ldots,n$. Further,
$i=1,\ldots,n$. Further, ![]() $(X_{11},\ldots,X_{n1} )$ is a pure isometric tuple as
$(X_{11},\ldots,X_{n1} )$ is a pure isometric tuple as ![]() $X_{K1}=\Pi_{i=1}^nX_{i1}$ is a pure isometry. Since
$X_{K1}=\Pi_{i=1}^nX_{i1}$ is a pure isometry. Since ![]() $Z_i=X_i^*$, we have that
$Z_i=X_i^*$, we have that ![]() $(Z_1|_{\mathscr{K}_1},\ldots,Z_n|_{\mathscr{K}_1})$ is pure co-isometric tuple and
$(Z_1|_{\mathscr{K}_1},\ldots,Z_n|_{\mathscr{K}_1})$ is pure co-isometric tuple and ![]() $(Z_1|_{\mathscr{K}_2},\ldots,Z_n|_{\mathscr{K}_2})$ is a unitary tuple. Hence, (ii) holds.
$(Z_1|_{\mathscr{K}_2},\ldots,Z_n|_{\mathscr{K}_2})$ is a unitary tuple. Hence, (ii) holds.
Additionally, if (5) holds, then the dilation ![]() $(X_1,\ldots,X_n)$ satisfies the condition that X is the Schäffer’s minimal isometric dilation of
$(X_1,\ldots,X_n)$ satisfies the condition that X is the Schäffer’s minimal isometric dilation of ![]() $T^*$ by Theorem 3.5. Let us denote
$T^*$ by Theorem 3.5. Let us denote ![]() $Z=X^*$. Then, Z is a co-isometry as X is an isometry and
$Z=X^*$. Then, Z is a co-isometry as X is an isometry and
 \begin{equation*}
Z=\begin{bmatrix}
T&D_{T^*}&0&0&\ldots\\
0&0&I_{\mathscr{D}_{T^*}}&0&\ldots\\
0&0&0&I_{\mathscr{D}_{T^*}}&\ldots\\
\vdots&\vdots&\vdots&\vdots&\ldots
\end{bmatrix}.
\end{equation*}
\begin{equation*}
Z=\begin{bmatrix}
T&D_{T^*}&0&0&\ldots\\
0&0&I_{\mathscr{D}_{T^*}}&0&\ldots\\
0&0&0&I_{\mathscr{D}_{T^*}}&\ldots\\
\vdots&\vdots&\vdots&\vdots&\ldots
\end{bmatrix}.
\end{equation*} Note that the dimensions of ![]() $\mathscr{D}_{Z}$ and
$\mathscr{D}_{Z}$ and ![]() $\mathscr{D}_{T}$ are same. Indeed, if
$\mathscr{D}_{T}$ are same. Indeed, if ![]() $\tau:\mathscr{D}_{T}\to \mathscr{D}_{Z}$ is defined by
$\tau:\mathscr{D}_{T}\to \mathscr{D}_{Z}$ is defined by ![]() $\tau D_{T}h=D_{Z}h$ for all
$\tau D_{T}h=D_{Z}h$ for all ![]() $h\in \mathscr{H}$ and extended continuously to the closure, then τ is a unitary. We recall the proof here. Since X is the minimal isometric dilation of
$h\in \mathscr{H}$ and extended continuously to the closure, then τ is a unitary. We recall the proof here. Since X is the minimal isometric dilation of ![]() $T^*$, we have
$T^*$, we have
Now for ![]() $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and ![]() $h\in \mathscr{H}$, we have
$h\in \mathscr{H}$, we have
Therefore, ![]() $D_{Z}X^nh=0$ for any
$D_{Z}X^nh=0$ for any ![]() $n\in \mathbb{N}$ and
$n\in \mathbb{N}$ and ![]() $h\in \mathscr{H}$. So,
$h\in \mathscr{H}$. So, ![]() $\mathscr{D}_{Z}=\overline{D_{Z}\mathscr{K}}=\overline{D_{Z}\mathscr{H}}.$ Also,
$\mathscr{D}_{Z}=\overline{D_{Z}\mathscr{K}}=\overline{D_{Z}\mathscr{H}}.$ Also,
Therefore, τ is a unitary. By Theorem 3.1, we have that
 \begin{equation*}
(X_{11},\ldots,X_{n1})\cong (M_{\widetilde{U}_1Q_1^{\perp}+z\widetilde{U}_1Q_1},\ldots, M_{\widetilde{U}_nQ_n^{\perp}+z\widetilde{U}_nQ_n}),
\end{equation*}
\begin{equation*}
(X_{11},\ldots,X_{n1})\cong (M_{\widetilde{U}_1Q_1^{\perp}+z\widetilde{U}_1Q_1},\ldots, M_{\widetilde{U}_nQ_n^{\perp}+z\widetilde{U}_nQ_n}),
\end{equation*} where ![]() $Q_1,\ldots,Q_n$ are projections and
$Q_1,\ldots,Q_n$ are projections and ![]() $\widetilde{U}_1,\ldots \widetilde{U}_n$ are commuting unitaries from
$\widetilde{U}_1,\ldots \widetilde{U}_n$ are commuting unitaries from  $\mathscr{B}(\mathscr{D}_{X_{K1}^*})$ satisfying
$\mathscr{B}(\mathscr{D}_{X_{K1}^*})$ satisfying
 \begin{equation}
D_{X_{i1}^{\prime *}}^2X_{i1}^*=D_{X_{K1}^*}Q_i^{\perp}\widetilde{U}_i^*D_{X_{K1}^*}
\end{equation}
\begin{equation}
D_{X_{i1}^{\prime *}}^2X_{i1}^*=D_{X_{K1}^*}Q_i^{\perp}\widetilde{U}_i^*D_{X_{K1}^*}
\end{equation}and
 \begin{equation}
D_{X_{i1}^*}^2X_{i1}^{\prime *}=D_{X_{K1}^*}\widetilde{U}_iQ_iD_{X_{K2}^*} \end{equation}
\begin{equation}
D_{X_{i1}^*}^2X_{i1}^{\prime *}=D_{X_{K1}^*}\widetilde{U}_iQ_iD_{X_{K2}^*} \end{equation} for all ![]() $i=1, \dots, n$. Using the fact that
$i=1, \dots, n$. Using the fact that ![]() $X_{i2},\ldots, X_{n2}$ are unitaries on
$X_{i2},\ldots, X_{n2}$ are unitaries on ![]() $\mathscr{K}_2$, it follows that
$\mathscr{K}_2$, it follows that
 \begin{align*}D_{X_i^{\prime *}}^2& =I_{\mathscr{K}}-\begin{bmatrix}
X_{i1}'&0\\
0&X_{i2}'
\end{bmatrix}\begin{bmatrix}
X_{i1}^{\prime *}&0\\
0&X_{i2}^{\prime *}
\end{bmatrix}\\
& =\begin{bmatrix}
I_{\mathscr{K}_1}-X_{i1}'X_{i1}^{\prime *}&0\\
0&I_{\mathscr{K}_2}-X_{i2}'X_{i2}^{\prime *}
\end{bmatrix}=\begin{bmatrix}
I_{\mathscr{K}_1}-X_{i1}'X_{i1}^{\prime *}&0\\
0&0
\end{bmatrix}.
\end{align*}
\begin{align*}D_{X_i^{\prime *}}^2& =I_{\mathscr{K}}-\begin{bmatrix}
X_{i1}'&0\\
0&X_{i2}'
\end{bmatrix}\begin{bmatrix}
X_{i1}^{\prime *}&0\\
0&X_{i2}^{\prime *}
\end{bmatrix}\\
& =\begin{bmatrix}
I_{\mathscr{K}_1}-X_{i1}'X_{i1}^{\prime *}&0\\
0&I_{\mathscr{K}_2}-X_{i2}'X_{i2}^{\prime *}
\end{bmatrix}=\begin{bmatrix}
I_{\mathscr{K}_1}-X_{i1}'X_{i1}^{\prime *}&0\\
0&0
\end{bmatrix}.
\end{align*} Therefore,  $D_{X_{i}^{\prime *}}=D_{X_{i1}^{\prime *}}\oplus 0$. Similarly, we can prove that
$D_{X_{i}^{\prime *}}=D_{X_{i1}^{\prime *}}\oplus 0$. Similarly, we can prove that  $D_{X_{i}^*}= D_{X_{i1}^*}\oplus 0$ for
$D_{X_{i}^*}= D_{X_{i1}^*}\oplus 0$ for ![]() $1\leq i \leq n$, with respect to the above decomposition of
$1\leq i \leq n$, with respect to the above decomposition of ![]() $\mathscr{K}$. So,
$\mathscr{K}$. So,  $D_{X^*}= D_{X_{K1}^*}\oplus0$. Hence
$D_{X^*}= D_{X_{K1}^*}\oplus0$. Hence  $\mathscr{D}_{X_{K1}^*}=\mathscr{D}_{X^*}=\mathscr{D}_{Z}$. Let us denote
$\mathscr{D}_{X_{K1}^*}=\mathscr{D}_{X^*}=\mathscr{D}_{Z}$. Let us denote ![]() $\widehat{U_i}=\tau^*\widetilde{U}_i\tau $ and
$\widehat{U_i}=\tau^*\widetilde{U}_i\tau $ and  $Q_i=\widehat{P_i}$ for
$Q_i=\widehat{P_i}$ for ![]() $1\leq i\leq n$. Thus,
$1\leq i\leq n$. Thus,  $\widehat{U_1},\ldots, \widehat{U_n}$ are commuting unitaries and
$\widehat{U_1},\ldots, \widehat{U_n}$ are commuting unitaries and  $\widehat{P_1},\ldots,\widehat{P_n}$ are projections in
$\widehat{P_1},\ldots,\widehat{P_n}$ are projections in ![]() $\mathscr{B}(\mathscr{D}(T))$ such that
$\mathscr{B}(\mathscr{D}(T))$ such that ![]() $(Z_1|_{\mathscr{K}_1},\ldots Z_n|_{\mathscr{K}_1})$ is unitarily equivalent to
$(Z_1|_{\mathscr{K}_1},\ldots Z_n|_{\mathscr{K}_1})$ is unitarily equivalent to  $\left( M_{\widetilde{U}_1Q_1^{\perp}+z\widetilde{U}_1Q_1},\ldots, M_{\widetilde{U}_nQ_n^{\perp}+z\widetilde{U}_nQ_n} \right)$, which can be realized as
$\left( M_{\widetilde{U}_1Q_1^{\perp}+z\widetilde{U}_1Q_1},\ldots, M_{\widetilde{U}_nQ_n^{\perp}+z\widetilde{U}_nQ_n} \right)$, which can be realized as  $\left( M_{\widehat{U_1}\widehat{P_1}^{\perp}+\widehat{U_1}\widehat{P_1}\bar{z}},\ldots,M_{\widehat{U_n}\widehat{P_n}^{\perp}+\widehat{U_n}\widehat{P_n}\bar{z}} \right) $ on
$\left( M_{\widehat{U_1}\widehat{P_1}^{\perp}+\widehat{U_1}\widehat{P_1}\bar{z}},\ldots,M_{\widehat{U_n}\widehat{P_n}^{\perp}+\widehat{U_n}\widehat{P_n}\bar{z}} \right) $ on ![]() $H^2(\mathscr{D}_{T})$ via the unitary τ. This proves (iii) and the proof is complete.
$H^2(\mathscr{D}_{T})$ via the unitary τ. This proves (iii) and the proof is complete.
Apart from having the explicit constructions of isometric dilations and functional model for a commuting contractive tuple, another interesting consequence of Theorem 3.5 is that it gives a commutant lifting in several variables as discussed in Remark 3.6. We conclude this article here. There will be two more articles in this direction as sequels. One of them will describe explicit constructions of minimal unitary dilations of commuting contractions ![]() $(T_1, \dots, T_n)$ on the minimal unitary dilation spaces of
$(T_1, \dots, T_n)$ on the minimal unitary dilation spaces of ![]() $T=\prod_{i=1}^n T_i$. The other article will deal with dilations when the defect spaces
$T=\prod_{i=1}^n T_i$. The other article will deal with dilations when the defect spaces ![]() $\mathscr{D}_T, \mathscr{D}_{T^*}$ are finite dimensional and their interplay with distinguished varieties in the polydisc.
$\mathscr{D}_T, \mathscr{D}_{T^*}$ are finite dimensional and their interplay with distinguished varieties in the polydisc.
Acknowledgements
S.P. is supported by the Seed Grant of IIT Bombay, the CPDA, and the ‘Core Research Grant’ with Award No. CRG/2023/005223 of Science and Engineering Research Board, India. P.S. has been supported by the PhD Fellowship of Council of Scientific and Industrial Research, India.
Data availability statement
(1) Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
(2) In case any datasets are generated during and/or analysed during the current study, they must be available from the corresponding author on reasonable request.