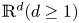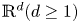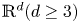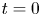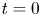1. Introduction
The compressible Navier–Stokes–Poisson equations are used to describe the motion of charged particles (i.e. the electrons and the holes or, the electrons and the ions) under the influence of the self-consistent electrostatic potential force arising from semiconductors and plasmas. In this model, the heavy holes and ions are assumed to be immobile and uniformly distributed in space, providing as a background of positive charge. The light electrons are modelled as a charged compressible fluid moving against the ionic forces. Neglecting magnetic effect and heat-conductive effect, the governing dynamics of the electron fluid are given by the following viscous isentropic compressible Navier–Stokes–Poisson equations (see [Reference Degond7, Reference Jüngel21, Reference Sitnko and Malnev35]):

for $(t,\,x)\in [0,\,\infty )\times \mathbb {R}^d(d\geq 1)$![]() . The unknown variables $n,\, u,\,\phi$
. The unknown variables $n,\, u,\,\phi$![]() are the electron density, the velocity and the electrostatic potential, $p(n)$
are the electron density, the velocity and the electrostatic potential, $p(n)$![]() is the pressure function, usually given by $p(\rho )=A\rho ^{\gamma }$
is the pressure function, usually given by $p(\rho )=A\rho ^{\gamma }$![]() with the constants $A>0$
with the constants $A>0$![]() and $\gamma \geq 1$
and $\gamma \geq 1$![]() . In this work, we assume that $p(n)$
. In this work, we assume that $p(n)$![]() is smooth and strictly increasing. $S(u)$
is smooth and strictly increasing. $S(u)$![]() denotes the viscous stress tensor with the form
denotes the viscous stress tensor with the form
here $\mu '$![]() and $\nu '$
and $\nu '$![]() are viscosity coefficients satisfying $\mu '>0$
are viscosity coefficients satisfying $\mu '>0$![]() and $\mu '+\nu '>0$
and $\mu '+\nu '>0$![]() for the sake of simplicity. The constant $m_e$
for the sake of simplicity. The constant $m_e$![]() is the ratio of the electron/ions mass, and $\lambda >0$
is the ratio of the electron/ions mass, and $\lambda >0$![]() is the Debye length. $N$
is the Debye length. $N$![]() stands for a given (constant) density of positively charged ions. Moreover, we also mention that, without viscous terms, (1.1) becomes the compressible isentropic Euler–Poisson system, which is another model describing the motion of charged particles. Finally, if the electrostatic potential $\phi$
stands for a given (constant) density of positively charged ions. Moreover, we also mention that, without viscous terms, (1.1) becomes the compressible isentropic Euler–Poisson system, which is another model describing the motion of charged particles. Finally, if the electrostatic potential $\phi$![]() is neglected, the compressible Navier–Stokes–Poisson equations (1.1) is then reduced to the classical compressible Navier–Stokes equations.
is neglected, the compressible Navier–Stokes–Poisson equations (1.1) is then reduced to the classical compressible Navier–Stokes equations.
Recently, some important progress has been made for the compressible Navier–Stokes–Poisson system. Here we only refer to some results about the isentropic compressible Navier–Stokes–Poisson system. The local and/or global existence of renormalized weak solutions to the Cauchy problem of the multi-dimensional compressible Navier–Stokes–Poisson system are proved in [Reference Ducomet14, Reference Zhang and Tan43]. The existence of non-trivial stationary solutions with compact support and their stability related to a free-boundary value problem for the three-dimensional Navier–Stokes–Poisson system are discussed in [Reference Ducomet15]. Some nonexistence result of global weak solutions is obtained in [Reference Chae5]. Large-time behaviour of the spherically symmetric Navier–Stokes–Poisson system with degenerate viscosity coefficients and with vacuum in $\mathbb {R}^3$![]() is shown in [Reference Zhang and Fang42]. The global existence of spherically symmetric weak solutions, and the regularity and long-time behaviour of global solution for free boundary value problem to three-dimensional spherically symmetric compressible Navier–Stokes–Poisson equations are shown in [Reference Kong and Li25]. The linear and nonlinear dynamical stability for the Lane–Emden solutions to the compressible Navier–Stokes–Poisson system is studied in [Reference Jang and Tice20]. The global strong solutions of the initial value problem for the multi-dimensional compressible Navier–Stokes–Poisson system with the strictly positive background profile in Besov spaces are investigated in [Reference Hao and Li19]. The global existence and $L^2$
is shown in [Reference Zhang and Fang42]. The global existence of spherically symmetric weak solutions, and the regularity and long-time behaviour of global solution for free boundary value problem to three-dimensional spherically symmetric compressible Navier–Stokes–Poisson equations are shown in [Reference Kong and Li25]. The linear and nonlinear dynamical stability for the Lane–Emden solutions to the compressible Navier–Stokes–Poisson system is studied in [Reference Jang and Tice20]. The global strong solutions of the initial value problem for the multi-dimensional compressible Navier–Stokes–Poisson system with the strictly positive background profile in Besov spaces are investigated in [Reference Hao and Li19]. The global existence and $L^2$![]() -decay rate of the smooth solution of the initial value problem for the compressible Navier–Stokes–Poisson system in $\mathbb {R}^3$
-decay rate of the smooth solution of the initial value problem for the compressible Navier–Stokes–Poisson system in $\mathbb {R}^3$![]() are proved in [Reference Li, Matsumura and Zhang27]. The pointwise estimates of the smooth solutions for the three-dimensional isentropic compressible Navier–Stokes–Poisson equation are obtained in [Reference Wang and Wu38]. The asymptotic stability of the nonlinear wave such as the rarefaction wave, the viscous shock wave and the stationary wave of the one-dimensional compressible Navier–Stokes–Poisson equation is studied in [Reference Duan and Liu12, Reference Duan, Liu and Zhang13, Reference Jiang, Lai, Yin and Zhu23, Reference Li and Zhu28, Reference Wang, Zhang and Zhang39].
are proved in [Reference Li, Matsumura and Zhang27]. The pointwise estimates of the smooth solutions for the three-dimensional isentropic compressible Navier–Stokes–Poisson equation are obtained in [Reference Wang and Wu38]. The asymptotic stability of the nonlinear wave such as the rarefaction wave, the viscous shock wave and the stationary wave of the one-dimensional compressible Navier–Stokes–Poisson equation is studied in [Reference Duan and Liu12, Reference Duan, Liu and Zhang13, Reference Jiang, Lai, Yin and Zhu23, Reference Li and Zhu28, Reference Wang, Zhang and Zhang39].
Moreover, the zero-electron-mass limit $m_e \to 0$![]() and the quasi-neutral limit $\lambda \to 0$
and the quasi-neutral limit $\lambda \to 0$![]() of the compressible Navier–Stokes–Poisson equations are the important problems in the theory of the compressible fluid of semiconductors and plasmas. Li and Liao [Reference Li and Liao26] showed the existence and zero-electron-mass limit of strong solutions to the stationary compressible Navier–Stokes–Poisson equation with large external force. Donatelli et al. [Reference Donatelli, Feireisl and Novotný10] discussed the vanishing electron-mass limit of weak solution for the plasma hydrodynamics in three-dimensional unbounded domain. Li et al. [Reference Li, Zhou and Liao29] investigated zero-electron-mass limit of the two-dimensional compressible Navier–Stokes–Poisson equations over bounded domain. The quasineutral limit of weak solution and smooth solutions of the compressible unipolar Navier–Stokes–Poisson system was studied in [Reference Donatelli and Marcati11, Reference Ju, Li and Li22, Reference Wang and Jiang37]. We also mention that many authors discussed the zero-electron-mass limit in the Euler–Poisson system for both well- and ill-prepared initial data, and we can refer to [Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4, Reference Xu and Yong40, Reference Xu and Zhang41] and some references therein. To our knowledge, there were no results on the zero-electron-mass limit of the classical local solutions to compressible Navier–Stokes–Poisson equations (1.1). The goal of this work is to fill in the void and study the zero-electron-mass limit of the classical solutions to compressible Navier–Stokes–Poisson equations (1.1) with well- and ill-prepared initial data in $\mathbb {R}^d(d\geq 1)$
of the compressible Navier–Stokes–Poisson equations are the important problems in the theory of the compressible fluid of semiconductors and plasmas. Li and Liao [Reference Li and Liao26] showed the existence and zero-electron-mass limit of strong solutions to the stationary compressible Navier–Stokes–Poisson equation with large external force. Donatelli et al. [Reference Donatelli, Feireisl and Novotný10] discussed the vanishing electron-mass limit of weak solution for the plasma hydrodynamics in three-dimensional unbounded domain. Li et al. [Reference Li, Zhou and Liao29] investigated zero-electron-mass limit of the two-dimensional compressible Navier–Stokes–Poisson equations over bounded domain. The quasineutral limit of weak solution and smooth solutions of the compressible unipolar Navier–Stokes–Poisson system was studied in [Reference Donatelli and Marcati11, Reference Ju, Li and Li22, Reference Wang and Jiang37]. We also mention that many authors discussed the zero-electron-mass limit in the Euler–Poisson system for both well- and ill-prepared initial data, and we can refer to [Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4, Reference Xu and Yong40, Reference Xu and Zhang41] and some references therein. To our knowledge, there were no results on the zero-electron-mass limit of the classical local solutions to compressible Navier–Stokes–Poisson equations (1.1). The goal of this work is to fill in the void and study the zero-electron-mass limit of the classical solutions to compressible Navier–Stokes–Poisson equations (1.1) with well- and ill-prepared initial data in $\mathbb {R}^d(d\geq 1)$![]() .
.
To study the zero-electron-mass limit of the Navier–Stokes–Poisson equations (1.1), we denote $\varepsilon ^2 = m_e$![]() , and we assume $\mu '=\varepsilon ^2\mu,\, \ \nu '=\varepsilon ^2\nu$
, and we assume $\mu '=\varepsilon ^2\mu,\, \ \nu '=\varepsilon ^2\nu$![]() . Moreover, let us introduce the electrostatic field $E=\nabla \phi$
. Moreover, let us introduce the electrostatic field $E=\nabla \phi$![]() and define the enthalpy $h=h(n)$
and define the enthalpy $h=h(n)$![]() by $h'(n) = p'(n) / n$
by $h'(n) = p'(n) / n$![]() and $h(1)=0$
and $h(1)=0$![]() . Then the viscous isentropic compressible Navier–Stokes–Poisson system (1.1) can be written as:
. Then the viscous isentropic compressible Navier–Stokes–Poisson system (1.1) can be written as:

where $\omega _{d-1}$![]() is the volume of the unit ball in $\mathbb {R} ^d$
is the volume of the unit ball in $\mathbb {R} ^d$![]() . From the analysis of [Reference Ali and Chen3], the operator $\Delta ^{-1}$
. From the analysis of [Reference Ali and Chen3], the operator $\Delta ^{-1}$![]() represents symbolically the fundamental solution of the Poisson equation, and $\Delta ^{-1}f$
represents symbolically the fundamental solution of the Poisson equation, and $\Delta ^{-1}f$![]() might not be well defined for not good enough functions $f$
might not be well defined for not good enough functions $f$![]() when the problem is considered on the whole space. However, $\nabla \Delta ^{-1} f$
when the problem is considered on the whole space. However, $\nabla \Delta ^{-1} f$![]() is well defined for $f \in H^s( \mathbb {R} ^d)$
is well defined for $f \in H^s( \mathbb {R} ^d)$![]() as long as $s>0$
as long as $s>0$![]() . Since we will prove the zero-electron-mass limit of the isentropic compressible Navier–Stokes–Poisson equations (1.2) with well- and ill-prepared initial data, we now supply the system (1.2) with the following initial data:
. Since we will prove the zero-electron-mass limit of the isentropic compressible Navier–Stokes–Poisson equations (1.2) with well- and ill-prepared initial data, we now supply the system (1.2) with the following initial data:
Moreover, for smooth solutions, the initial value problem (1.2)–(1.3) is equivalent to the following hyperbolic–parabolic type system:

with initial conditions
Here $n(h)$![]() is a smooth reversible function of $h(n)$
is a smooth reversible function of $h(n)$![]() , which can be assured by the assumption of $p(n)$
, which can be assured by the assumption of $p(n)$![]() .
.
The zero-electron-mass limit $\varepsilon \rightarrow 0$![]() in the problem (1.2)–(1.3) or (1.4)–(1.5) is reminiscent of the low Mach number (incompressible) limit of the compressible fluid equation, which has been investigated in a number of recent studies, see the monograph [Reference Danchin6] and the survey papers [Reference Alazard2, Reference Feireisl and Novotny16, Reference Masmoudi30, Reference Schochet32], and the references cited therein. The objective of this paper is to perform the limit as $\varepsilon \to 0$
in the problem (1.2)–(1.3) or (1.4)–(1.5) is reminiscent of the low Mach number (incompressible) limit of the compressible fluid equation, which has been investigated in a number of recent studies, see the monograph [Reference Danchin6] and the survey papers [Reference Alazard2, Reference Feireisl and Novotny16, Reference Masmoudi30, Reference Schochet32], and the references cited therein. The objective of this paper is to perform the limit as $\varepsilon \to 0$![]() in (1.2). Then as in [Reference Ali and Chen3, Reference Desjardins and Grenier8, Reference Dasjardins, Grenier, Lions and Masmoudi9, Reference Masmoudi30], we introduce the new variables:
in (1.2). Then as in [Reference Ali and Chen3, Reference Desjardins and Grenier8, Reference Dasjardins, Grenier, Lions and Masmoudi9, Reference Masmoudi30], we introduce the new variables:
then systems (1.2) and (1.4) are rewritten as

and

respectively, where $A( \varepsilon \tilde h ) = 1/ p' (n(h^0 + \varepsilon \tilde h ))$![]() . For smooth solutions, we use the variable $\tilde h$
. For smooth solutions, we use the variable $\tilde h$![]() instead of $\tilde n$
instead of $\tilde n$![]() , because the system (1.7) with some symmetric part is more convenient for standard energy estimates.
, because the system (1.7) with some symmetric part is more convenient for standard energy estimates.
Notations. First, $L^p(\mathbb {R}^d)$![]() with $1\leq p<\infty$
with $1\leq p<\infty$![]() denotes the space of measurable functions whose $p$
denotes the space of measurable functions whose $p$![]() -powers are integrable on $\mathbb {R}^d$
-powers are integrable on $\mathbb {R}^d$![]() , with norm $\|\cdot \|_{L^p}=(\int _{\mathbb {R}^d}|\cdot |^p{\rm d}x)^{1/p}$
, with norm $\|\cdot \|_{L^p}=(\int _{\mathbb {R}^d}|\cdot |^p{\rm d}x)^{1/p}$![]() , and $L^\infty (\mathbb {R}^d)$
, and $L^\infty (\mathbb {R}^d)$![]() is the space of bounded measurable functions on $\mathbb {R}^d$
is the space of bounded measurable functions on $\mathbb {R}^d$![]() , with the norm $\|\cdot \|_{L^\infty }=\mathrm {ess sup}_{x\in \mathbb {R}^d}|\cdot |$
, with the norm $\|\cdot \|_{L^\infty }=\mathrm {ess sup}_{x\in \mathbb {R}^d}|\cdot |$![]() . Without confusion, we also denote the norm of $L^2(\mathbb {R}^d)$
. Without confusion, we also denote the norm of $L^2(\mathbb {R}^d)$![]() by $\|\cdot \|$
by $\|\cdot \|$![]() for brevity. Next, for a nonnegative integer $k$
for brevity. Next, for a nonnegative integer $k$![]() , $H^k=H^k(\mathbb {R}^d)$
, $H^k=H^k(\mathbb {R}^d)$![]() denotes the usual $L^2$
denotes the usual $L^2$![]() -type Sobolev space of order $k$
-type Sobolev space of order $k$![]() . We also write $\|\cdot \|_k$
. We also write $\|\cdot \|_k$![]() for the standard norm of $H^k(\mathbb {R}^d)$
for the standard norm of $H^k(\mathbb {R}^d)$![]() . Moreover, we denote ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert \cdot \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }_{s,T} = \sup \nolimits _{0< t< T} \| \cdot \|_s$
. Moreover, we denote ${\left \vert \kern -0.25ex\left \vert \kern -0.25ex\left \vert \cdot \right \vert \kern -0.25ex\right \vert \kern -0.25ex\right \vert }_{s,T} = \sup \nolimits _{0< t< T} \| \cdot \|_s$![]() for $s\geq 0$
for $s\geq 0$![]() . In addition, we denote by $C([0,\, T],\, {\bf X})$
. In addition, we denote by $C([0,\, T],\, {\bf X})$![]() (resp. $L^2([0,\, T],\, {\bf X})$
(resp. $L^2([0,\, T],\, {\bf X})$![]() ) the space of continuous (resp. square integrable) functions on $[0,\, T]$
) the space of continuous (resp. square integrable) functions on $[0,\, T]$![]() with values in a Banach space ${\bf X}$
with values in a Banach space ${\bf X}$![]() . Finally, the symbols $c_i\ (i=1,\,2,\,\ldots )$
. Finally, the symbols $c_i\ (i=1,\,2,\,\ldots )$![]() or $C_j\ (j=0,\,1,\,2,\,\ldots )$
or $C_j\ (j=0,\,1,\,2,\,\ldots )$![]() are always used to denote generic positive constants independent of $\varepsilon$
are always used to denote generic positive constants independent of $\varepsilon$![]() , $c(\cdot )$
, $c(\cdot )$![]() and $C(\cdot )$
and $C(\cdot )$![]() denote some positive smooth functions which may vary from line to line.
denote some positive smooth functions which may vary from line to line.
The first result in this paper is the following uniform local existence.
Theorem 1.1 (Uniform-in-$\varepsilon$ local-in-time existence)
local-in-time existence)
Let $d\geq 1,\, s>d/2+2$![]() and $N>0,$
and $N>0,$![]() assume that the initial data $(n_I^\varepsilon,\, u_I^\varepsilon )$
assume that the initial data $(n_I^\varepsilon,\, u_I^\varepsilon )$![]() satisfy
satisfy

where $M_0$![]() a given constant independent of $\varepsilon$
a given constant independent of $\varepsilon$![]() . Then there exist constants $T_0>0$
. Then there exist constants $T_0>0$![]() and $M_0'>0$
and $M_0'>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() , and $\varepsilon _0(M_0)>0$
, and $\varepsilon _0(M_0)>0$![]() , such that, for all $\varepsilon$
, such that, for all $\varepsilon$![]() with $0< \varepsilon < \varepsilon _0(M_0)$
with $0< \varepsilon < \varepsilon _0(M_0)$![]() , the problem (1.2)–(1.3) has a classical solution $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$
, the problem (1.2)–(1.3) has a classical solution $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$![]() in $[0,\, T_0]$
in $[0,\, T_0]$![]() satisfying
satisfying
Next, we have the following zero-electron-mass limit for the problem (1.2)–(1.3) with well-prepared initial data, that is, the initial data is prepared to make the ‘initial time-derivatives’ uniformly bounded. Here the ‘initial time-derivative’ is understood by compatibility condition using the differential equation that time-derivative can be replaced by spatial-derivatives. The term ill-prepared initial data refers to that is not well-prepared.
Theorem 1.2 (Limit for well-prepared initial data)
Let the assumption of theorem 1.1 be held. Assume that the initial data are well-prepared, that is, $u_I^\varepsilon =u_I^0+\varepsilon u_I^1$![]() with $\nabla \cdot u_I^0 = 0,$
with $\nabla \cdot u_I^0 = 0,$![]() and
and
where $M_1$![]() is a constant. Let $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$
is a constant. Let $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$![]() be a classical solution to (1.2)–(1.3) in $[0,\, T_0]$
be a classical solution to (1.2)–(1.3) in $[0,\, T_0]$![]() with $T_0>0$
with $T_0>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() as obtained in theorem 1.1. Then we have the limit as $\varepsilon \to 0$
as obtained in theorem 1.1. Then we have the limit as $\varepsilon \to 0$![]() that
that
where $u^0$![]() is the unique classical solution of the incompressible Navier–Stokes equations
is the unique classical solution of the incompressible Navier–Stokes equations

and $\pi$![]() is the limit of
is the limit of
Finally, for the ill-prepared initial data of the problem (1.2)–(1.3), we have
Theorem 1.3 (Limit for ill-prepared initial data)
Let the assumptions of theorem 1.1 hold and let $d\geq 3,$![]() suppose that the initial data $u^\varepsilon _I \to u^0_I$
suppose that the initial data $u^\varepsilon _I \to u^0_I$![]() in $H^s (\mathbb {R}^d)$
in $H^s (\mathbb {R}^d)$![]() as $\varepsilon \to 0,$
as $\varepsilon \to 0,$![]() and let $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$
and let $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$![]() be a classical solution to (1.2)–(1.3) in $[0,\, T_0]$
be a classical solution to (1.2)–(1.3) in $[0,\, T_0]$![]() with $T_0>0$
with $T_0>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() . Then, as $\varepsilon \to 0,$
. Then, as $\varepsilon \to 0,$![]()

where $u^0_* \in L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) )$![]() is the solution of the incompressible Navier–Stokes equations
is the solution of the incompressible Navier–Stokes equations

for some $\pi \in L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) ),$![]() and $P$
and $P$![]() is the orthogonal projection of $H^s$
is the orthogonal projection of $H^s$![]() onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$
onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$![]() .
.
Remark 1.4 Theorem 1.3 holds only for $d\geq 3$![]() , since the decay property of the fundamental solution is essentially used in the spectral analysis. This is compatible with the corresponding result in [Reference Ali and Chen3].
, since the decay property of the fundamental solution is essentially used in the spectral analysis. This is compatible with the corresponding result in [Reference Ali and Chen3].
Remark 1.5 In the present work, we only discuss the zero-electron-mass limit for the unipolar isentropic Navier–Stokes–Poisson equation with well-prepared and ill-prepared initial data. It is also attractive for studying similar problems for the unipolar non-isentropic and bipolar compressible Navier–Stokes–Poisson system. These are expected to be done in the forthcoming papers.
The ideas and outlines of proving theorems 1.1, 1.2 and 1.3 are as follows. As a first step, we will get the uniform-in-$\varepsilon$![]() estimate in short time using a similar idea as in [Reference Alazard1, Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4]. Then applying the local existence of [Reference Kawashima24] and standard continuation argument, we can show theorem 1.1. To get the uniform estimate, we need to treat the singular terms with $\frac {1}{\varepsilon }$
estimate in short time using a similar idea as in [Reference Alazard1, Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4]. Then applying the local existence of [Reference Kawashima24] and standard continuation argument, we can show theorem 1.1. To get the uniform estimate, we need to treat the singular terms with $\frac {1}{\varepsilon }$![]() . Note that the terms $\frac {1}{\varepsilon } \mathrm {div} \, u$
. Note that the terms $\frac {1}{\varepsilon } \mathrm {div} \, u$![]() and $\frac {1}{\varepsilon } \nabla \tilde h$
and $\frac {1}{\varepsilon } \nabla \tilde h$![]() in (1.6) are symmetric, the key ingredient of the uniform local estimate is the control of the term $\frac {1}{\varepsilon } \tilde E$
in (1.6) are symmetric, the key ingredient of the uniform local estimate is the control of the term $\frac {1}{\varepsilon } \tilde E$![]() in (1.6), which can be similarly estimated as in [Reference Ali and Chen3]. Then, after obtaining the estimate of time derivatives with a similar argument as the one used in [Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4], the zero-electron-mass limit for the well-prepared initial data on $\mathbb {R}^d(d\geq 1)$
in (1.6), which can be similarly estimated as in [Reference Ali and Chen3]. Then, after obtaining the estimate of time derivatives with a similar argument as the one used in [Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4], the zero-electron-mass limit for the well-prepared initial data on $\mathbb {R}^d(d\geq 1)$![]() can be achieved by using Aubin's lemma. We will prove theorem 1.2 in § 4.
can be achieved by using Aubin's lemma. We will prove theorem 1.2 in § 4.
For the proof of theorem 1.3, we still follow the approach of [Reference Grenier17, Reference Grenier18, Reference Ukai36], which was used in [Reference Ali and Chen3]. That is, we first consider the linearized Navier–Stokes–Poisson equations, and next study the properties of the semigroup $\mathcal {L}^\varepsilon (t)$![]() generated by the linear operator. Then we can decompose the solution $(\tilde {n},\,u)=(0,\,u_1)+(\tilde {n},\,u_2)$
generated by the linear operator. Then we can decompose the solution $(\tilde {n},\,u)=(0,\,u_1)+(\tilde {n},\,u_2)$![]() with $u_1$
with $u_1$![]() being the divergence free part. Finally, by further use of the properties of $\mathcal {L}^\varepsilon (t)$
being the divergence free part. Finally, by further use of the properties of $\mathcal {L}^\varepsilon (t)$![]() , it is possible to get estimates for $\partial _tu_1$
, it is possible to get estimates for $\partial _tu_1$![]() , which help the discussion of the convergence away from ${t = 0}$
, which help the discussion of the convergence away from ${t = 0}$![]() . Therefore, we can prove the limit for ill-prepared initial data in § 5. It is worth noting that the eigenvalues of the linear compressible Navier–Stokes–Poisson equations are different from that of the linear compressible Euler equations in [Reference Grenier17, Reference Grenier18, Reference Ukai36] and that of the linear compressible Euler–Poisson equations in [Reference Ali and Chen3]. The solution of the linearized equation in [Reference Grenier17, Reference Grenier18, Reference Ukai36] has an algebra decay rate, and the solution of the linearized equation in [Reference Ali and Chen3] has an exponential decay rate due to the damping. However, the dissipation mechanism for the linear compressible Navier–Stokes–Poisson system is different here, which can be seen from its eigenvalues
. Therefore, we can prove the limit for ill-prepared initial data in § 5. It is worth noting that the eigenvalues of the linear compressible Navier–Stokes–Poisson equations are different from that of the linear compressible Euler equations in [Reference Grenier17, Reference Grenier18, Reference Ukai36] and that of the linear compressible Euler–Poisson equations in [Reference Ali and Chen3]. The solution of the linearized equation in [Reference Grenier17, Reference Grenier18, Reference Ukai36] has an algebra decay rate, and the solution of the linearized equation in [Reference Ali and Chen3] has an exponential decay rate due to the damping. However, the dissipation mechanism for the linear compressible Navier–Stokes–Poisson system is different here, which can be seen from its eigenvalues

this is somehow similar to that of heat equation, and the fundamental solution contains some part like the heat kernel, and a big difficulty is the singularity of the heat kernel at $t=0$![]() . Next, we have the characteristic decomposition of the solution operator in the form (5.3), with each mode corresponding to an eigenvalue, and then analyse carefully the uniform-in-$\varepsilon$
. Next, we have the characteristic decomposition of the solution operator in the form (5.3), with each mode corresponding to an eigenvalue, and then analyse carefully the uniform-in-$\varepsilon$![]() estimates of each mode. See lemma 5.1 for details. Due to the singularity of the heat kernel at $t=0$
estimates of each mode. See lemma 5.1 for details. Due to the singularity of the heat kernel at $t=0$![]() and good decay away from $t=0$
and good decay away from $t=0$![]() , we need to have more precise local in time estimate of the solution operator such that the result is integrable in time. Thus we need two sets of estimates: $t<\delta$
, we need to have more precise local in time estimate of the solution operator such that the result is integrable in time. Thus we need two sets of estimates: $t<\delta$![]() and $t\geq \delta$
and $t\geq \delta$![]() , for any given positive constant $\delta$
, for any given positive constant $\delta$![]() . Without loss of generality, we consider $\delta =1$
. Without loss of generality, we consider $\delta =1$![]() , that is, we derive the estimate (5.6) for $t<1$
, that is, we derive the estimate (5.6) for $t<1$![]() , and, estimate (5.7) for $t\geq 1$
, and, estimate (5.7) for $t\geq 1$![]() . The solution of the full linearized problem (5.1) can be represented by Duhamel's principle using the solution operator of the linear part, which essentially relies on the time integrability of the estimate near $t=0$
. The solution of the full linearized problem (5.1) can be represented by Duhamel's principle using the solution operator of the linear part, which essentially relies on the time integrability of the estimate near $t=0$![]() . See also remark 5.2. Another difficulty in the analysis is due to the complicated structure of the eigenvalues $\lambda _\pm$
. See also remark 5.2. Another difficulty in the analysis is due to the complicated structure of the eigenvalues $\lambda _\pm$![]() . More specifically, the term inside the square-root in $\lambda _\pm$
. More specifically, the term inside the square-root in $\lambda _\pm$![]() , $F(|\xi |^2) := 4 (1+a|\xi |^2) - (\mu +\nu )^2 |\xi |^4 \varepsilon ^2$
, $F(|\xi |^2) := 4 (1+a|\xi |^2) - (\mu +\nu )^2 |\xi |^4 \varepsilon ^2$![]() , is not monotone with respect to $|\xi |^2$
, is not monotone with respect to $|\xi |^2$![]() , unlike $\tilde F(|\xi |^2)= 4 (1+a|\xi |^2) - \varepsilon ^2$
, unlike $\tilde F(|\xi |^2)= 4 (1+a|\xi |^2) - \varepsilon ^2$![]() for the Euler–Poisson case which was strictly increasing, will bring difficulty to our analysis. To deal with this problem, we properly decompose the solution operator with respect to frequencies, say, the low, medium and high frequency parts, and estimate each part respectively. See (5.13) and subsequent computations for details.
for the Euler–Poisson case which was strictly increasing, will bring difficulty to our analysis. To deal with this problem, we properly decompose the solution operator with respect to frequencies, say, the low, medium and high frequency parts, and estimate each part respectively. See (5.13) and subsequent computations for details.
This paper is organized as follows. In the next section we state some useful lemmas which will be used later, then we give the uniform local estimate of the terms involving the term $\frac {1}{\varepsilon } \tilde E$![]() . We will prove the uniform local existence of the compressible Navier–Stokes–Poisson equation in § 3. Finally, the limit for the solutions of the compressible Navier–Stokes–Poisson equation with well- and ill-prepared initial data will be considered in § 4 and § 5, respectively.
. We will prove the uniform local existence of the compressible Navier–Stokes–Poisson equation in § 3. Finally, the limit for the solutions of the compressible Navier–Stokes–Poisson equation with well- and ill-prepared initial data will be considered in § 4 and § 5, respectively.
2. Preliminary
We make some preliminaries in this section, by first giving some useful lemmas which will be used later, then showing the uniform local estimate of the term involving the term $\frac {1}{\varepsilon } \tilde E$![]() . To begin with, we list the following classical differential inequalities in Sobolev spaces [Reference Majda31].
. To begin with, we list the following classical differential inequalities in Sobolev spaces [Reference Majda31].
Lemma 2.1 (i) Let $f,\, g\in H^s(\mathbb {R}^d)$![]() for $s\geq \frac d2+1$
for $s\geq \frac d2+1$![]() . Then, for all multi-indices $\alpha$
. Then, for all multi-indices $\alpha$![]() with $|\alpha |\leq s,$
with $|\alpha |\leq s,$![]() it holds that $\partial _x^\alpha (fg)\in L^2(\mathbb {R}^d)$
it holds that $\partial _x^\alpha (fg)\in L^2(\mathbb {R}^d)$![]() and
and
(ii) Let $f\in H^s(\mathbb {R}^d)$![]() and $g\in H^{s-1}(\mathbb {R}^d)$
and $g\in H^{s-1}(\mathbb {R}^d)$![]() for $s\geq \frac d2+2$
for $s\geq \frac d2+2$![]() . Then for all multi-indices $\alpha$
. Then for all multi-indices $\alpha$![]() with $|\alpha |\leq s,$
with $|\alpha |\leq s,$![]() it holds that the commutator $[\partial _x^\alpha,\, f]g\in L^2(\mathbb {R}^d)$
it holds that the commutator $[\partial _x^\alpha,\, f]g\in L^2(\mathbb {R}^d)$![]() and
and
(iii) Assume $g(u)$![]() is a smooth function on $G,$
is a smooth function on $G,$![]() $u(x)$
$u(x)$![]() is a continuous function with $u(x)\in G_1,$
is a continuous function with $u(x)\in G_1,$![]() $\bar {G}_1\subset \subset G,$
$\bar {G}_1\subset \subset G,$![]() and $u(x)\in L^\infty \cap H^s(\mathbb {R}^d)$
and $u(x)\in L^\infty \cap H^s(\mathbb {R}^d)$![]() . Then for $s\geq 1$
. Then for $s\geq 1$![]() ,
,
Here $|\cdot |_{r,\bar {G}_1}$![]() is the $C^r$
is the $C^r$![]() -norm on the set $\bar {G}_1$
-norm on the set $\bar {G}_1$![]() and $C_s$
and $C_s$![]() is a generic constant depending only on $s$
is a generic constant depending only on $s$![]() .
.
Next, we recall the following Aubin's lemma in [Reference Simon33, Reference Simon34].
Lemma 2.2 Assume $X\subset E\subset Y$![]() are Banach spaces and $X\hookrightarrow \hookrightarrow Y$
are Banach spaces and $X\hookrightarrow \hookrightarrow Y$![]() . Then the following imbeddings are compact:
. Then the following imbeddings are compact:
(i) $\Big \{\varphi :\varphi \in L^q(0,\,T;X),\,\frac {\partial \varphi }{\partial t}\in L^1(0,\,T;Y)\Big \}\hookrightarrow \hookrightarrow L^q(0,\,T;E)$
 , if $1\leq q\leq \infty$
, if $1\leq q\leq \infty$ ;
;(ii) $\Big \{\varphi :\varphi \in L^\infty (0,\,T;X),\,\frac {\partial \varphi }{\partial t}\in L^\gamma (0,\,T;Y)\Big \}\hookrightarrow \hookrightarrow C(0,\,T;E)$
 , if $1<\gamma \leq \infty$
, if $1<\gamma \leq \infty$ .
.
To end this section, we give the following estimates of the terms involving the term such as $\frac {1}{\varepsilon } \tilde E$![]() .
.
Lemma 2.3 Under the assumptions of theorem 1.1, let $(\tilde h,\, u,\, \tilde E)$![]() be the solution of the Cauchy problem for (1.7) with (1.5) in $[0,\, T^*]$
be the solution of the Cauchy problem for (1.7) with (1.5) in $[0,\, T^*]$![]() for some $T^*>0$
for some $T^*>0$![]() (may depend on $\varepsilon$
(may depend on $\varepsilon$![]() ), and (3.1) hold. Then we have
), and (3.1) hold. Then we have
and
Furthermore, for any multi-index $\alpha$![]() with $1\leq |\alpha | \leq s$
with $1\leq |\alpha | \leq s$![]() , denote
, denote
we also have

The proof is similar to that in [Reference Ali and Chen3], thus is omitted here.
3. Uniform local existence
In this section, we mainly show uniform-in-$\varepsilon$![]() local existence of smooth solution for (1.2)–(1.3). That is, we prove theorem 1.1. Applying the local existence of [Reference Kawashima24] and standard continuation argument, we only need the following uniform a priori estimate.
local existence of smooth solution for (1.2)–(1.3). That is, we prove theorem 1.1. Applying the local existence of [Reference Kawashima24] and standard continuation argument, we only need the following uniform a priori estimate.
Lemma 3.1 (Uniform-in-$\varepsilon$ a priori estimates)
a priori estimates)
Under the assumptions of theorem 1.1, let $(\tilde h,\, u,\, \tilde E)$![]() be the solution of the Cauchy problem for (1.7) with (1.5) in $[0,\, T^*]$
be the solution of the Cauchy problem for (1.7) with (1.5) in $[0,\, T^*]$![]() for some $T^*>0$
for some $T^*>0$![]() (may depend on $\varepsilon$
(may depend on $\varepsilon$![]() ), and
), and
for some positive constant $M$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() . Then there exist $\varepsilon _0 =\varepsilon _0(M)$
. Then there exist $\varepsilon _0 =\varepsilon _0(M)$![]() and $c(M)>0$
and $c(M)>0$![]() such that for all $0<\varepsilon <\varepsilon _0,$
such that for all $0<\varepsilon <\varepsilon _0,$![]() it holds that
it holds that
Before the proof of lemma 3.1, we give some necessary preliminaries. First, from (3.1) and Sobolev inequalities, it is easy to see that, there exists a constant $C(M)>0$![]() , such that, for $|\alpha |\leq 2$
, such that, for $|\alpha |\leq 2$![]() ,
,
and
for sufficiently small $\varepsilon$![]() . Furthermore, since
. Furthermore, since
we also have
Moreover, using (1.7) $_1$![]() , we have
, we have
and

which together with (3.3)–(3.4) imply
Proof of lemma 3.1. Multiply (1.7) $_1$![]() and (1.7) $_2$
and (1.7) $_2$![]() by $\tilde h$
by $\tilde h$![]() and $u$
and $u$![]() , respectively, take the summation and integrate over $\mathbb {R}^d$
, respectively, take the summation and integrate over $\mathbb {R}^d$![]() , then we have
, then we have

First, utilizing (3.3), (3.5) and (3.6), it is trivial that
Next, by using Cauchy's inequality and (3.3), we have
Finally, from (2.1) in lemma 2.3, we have
Hence, putting the estimates (3.8)–(3.10) into (3.7), using (3.3) and (3.4), we get

Next, we derive the estimates of derivatives of $(\tilde h ,\, u,\, \tilde E)$![]() . Let $\alpha$
. Let $\alpha$![]() be a multi-index with $1\leq |\alpha | \leq s$
be a multi-index with $1\leq |\alpha | \leq s$![]() , denote $h_\alpha = D^\alpha \tilde h, \ u_\alpha = D^\alpha u, \ E_\alpha = D^\alpha \tilde E$
, denote $h_\alpha = D^\alpha \tilde h, \ u_\alpha = D^\alpha u, \ E_\alpha = D^\alpha \tilde E$![]() , and define $| D^{|\alpha |} u | := \sup \nolimits _\alpha | D^\alpha u|$
, and define $| D^{|\alpha |} u | := \sup \nolimits _\alpha | D^\alpha u|$![]() . Then applying the operator $D^\alpha$
. Then applying the operator $D^\alpha$![]() to (1.7), we have
to (1.7), we have

where

In fact $|\beta | = |\alpha | - 1$![]() here. Now multiply (3.12) $_1$
here. Now multiply (3.12) $_1$![]() and (3.12) $_2$
and (3.12) $_2$![]() by $h_\alpha$
by $h_\alpha$![]() and $u_\alpha$
and $u_\alpha$![]() , respectively, and integrate the resultant equations over $\mathbb {R}^d$
, respectively, and integrate the resultant equations over $\mathbb {R}^d$![]() , then the summation of the two equations yields
, then the summation of the two equations yields

First, using (3.3) and (3.6), it is easy to find that
Second, by using Cauchy's inequality and (3.3), we have
and similarly,

Next, from (2.3) in lemma 2.3, we have

Finally, from lemma 2.1 and (3.4), we have

and similarly, we have
thus, by using Cauchy–Schwarz's inequality, we obtain
Putting the estimates (3.14)–(3.18) into (3.13), using again (3.3) and (3.4), we readily have

Finally, taking summation (3.11) and (3.19) for $1\leq \alpha |\leq s$![]() , we have
, we have

which together with Gronwall's inequality imply (3.2), this completes the proof of lemma 3.1.
4. Limit for well-prepared initial data
In this section, we consider the zero-electron-mass limit of the isentropic compressible Navier–Stokes–Poisson equation with well-prepared initial data, that is, we shall prove theorem 1.2. Similar to that in [Reference Ali and Chen3, Reference Ali, Chen, Jüngel and Peng4], we need the following uniform estimates of the time derivatives.
Lemma 4.1 Under the assumptions of theorem 1.2 and lemma 3.1, there exists $\varepsilon _1 \in (0,\, \varepsilon _0)$![]() such that for all $0<\varepsilon < \varepsilon _1,$
such that for all $0<\varepsilon < \varepsilon _1,$![]() it holds that
it holds that

Proof. Take time derivative to (1.7), we have

where

Multiply (4.2) $_1$![]() and (4.2) $_2$
and (4.2) $_2$![]() by $\tilde h_t$
by $\tilde h_t$![]() and $u_t$
and $u_t$![]() , respectively, then integrate over $\mathbb {R}^d$
, respectively, then integrate over $\mathbb {R}^d$![]() and take the summation, we get
and take the summation, we get

Similar to (3.8) and (3.14), one has
Next, similar to (3.9) and (3.15), one has
For $J_3$![]() , by using lemma 2.3, we have
, by using lemma 2.3, we have
Finally, by using Cauchy inequality, (3.3) and (3.4), we have
Now, put (4.4)–(4.7) into (4.3), and noting (3.4), we have

Moreover, from (1.7) $_1$![]() and $u_I^\varepsilon =u_I^0+\varepsilon u_I^1$
and $u_I^\varepsilon =u_I^0+\varepsilon u_I^1$![]() with $\nabla \cdot u_I^0 =0$
with $\nabla \cdot u_I^0 =0$![]() , we know
, we know
Similarly, with the condition (1.10), we also have
Then, apply Gronwall's inequality to (4.8), by noting (4.9)–(4.10), we readily have (4.1). This completes the proof.
Now we show the proof of theorem 1.2.
Proof Proof of theorem 1.2
thus, as $\varepsilon \to 0$![]() ,
,
and further by lemma 2.2, there exist a subsequence, still denoted by $u^\varepsilon$![]() , such that as $\varepsilon \to 0$
, such that as $\varepsilon \to 0$![]() ,
,
It remains to show (1.11). In fact, it holds for all $\chi (t) \in C^\infty [0,\, T_0]$![]() and $\psi (x) \in C_0^\infty (\mathbb {R}^d; \mathbb {R}^d )$
and $\psi (x) \in C_0^\infty (\mathbb {R}^d; \mathbb {R}^d )$![]() such that $\nabla \cdot \psi = 0$
such that $\nabla \cdot \psi = 0$![]() ,
,

Then passing the limit as $\varepsilon \to 0$![]() in above equation to get
in above equation to get

By the definition of weak time derivative of $u^0$![]() , we conclude that
, we conclude that
where $P$![]() is the standard projection on the set of divergence-free vector fields. Since we already have
is the standard projection on the set of divergence-free vector fields. Since we already have
which implies that
we infer
Thus, $u^0 \in C^1 ( [0,\, T_0]\times (\mathbb {R}^d) )$![]() is a classical solution to
is a classical solution to
The second equation and the regularity of $\partial _t u^0+ u^0 \cdot \nabla u^0 -({\mu }/{ N }) \Delta u^0$![]() show that there exists a function $\pi \in L^\infty ([0,\,T_0]; H^s(\mathbb {R}^d))$
show that there exists a function $\pi \in L^\infty ([0,\,T_0]; H^s(\mathbb {R}^d))$![]() such that
such that
Further, taking into account the equation satisfied by $u^\varepsilon$![]() and
and
weakly* in $L^\infty ([0,\,T];L^2(\mathbb {R}^d))$![]() , we get
, we get
Finally, the uniqueness of smooth solutions to the incompressible Navier–Stokes equation implies the convergence of the whole sequence. This completes the proof.
5. Limit for ill-prepared initial data
In this section, we study the zero-electron-mass limit of the initial value problem (1.2)–(1.3) with ill-prepared initial data. To begin with, we rewrite (1.6) into the following linearized form:

where

Further, we set $N = 1$![]() without loss of generality, and denote $a= h'(N)$
without loss of generality, and denote $a= h'(N)$![]() . Let us consider the Cauchy problem of the linear part of (5.1):
. Let us consider the Cauchy problem of the linear part of (5.1):
where the linear operator
Let $\mathcal {L}^\varepsilon (t)$![]() be the semigroup generated by $L$
be the semigroup generated by $L$![]() , then $U(x,\,t) = \mathcal {L}^\varepsilon (t) U_I(x)$
, then $U(x,\,t) = \mathcal {L}^\varepsilon (t) U_I(x)$![]() solves Cauchy problem (5.2). We have
solves Cauchy problem (5.2). We have
Lemma 5.1 Assume $U_I \in L^1\cap H^s$![]() . The solution of (5.2) can be decomposed as
. The solution of (5.2) can be decomposed as
in which (i)
where $\mathcal {G}(x,\,t) =( {1}/{( 4\pi \mu t)})^{d/2} \exp (- ({|x|^2}/{ 4 \mu t}))$![]() is the heat kernel, $P$
is the heat kernel, $P$![]() is the orthogonal projection of $H^s$
is the orthogonal projection of $H^s$![]() onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$
onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$![]() , and
, and
(ii) For $t<1$![]() and $\theta \in (0,\, \frac {1}{ d}),$
and $\theta \in (0,\, \frac {1}{ d}),$![]()

(iii) For $t\geq 1,$![]()
(iv) Furthermore, for any fixed $\tau >0,$![]()
Remark 5.2 Note that (5.6), the local-in-time behaviour of the solution, is essential for the estimate of the full nonlinear system when we apply Duhamel's principle, since the singularity at $t=0$![]() in (5.6) is integrable. The three terms on the right hand side of (5.6) correspond to low, medium and high frequency part, respectively. On the other hand, if the solution exist for longer time, the behaviour of the solution is controlled by (5.7).
in (5.6) is integrable. The three terms on the right hand side of (5.6) correspond to low, medium and high frequency part, respectively. On the other hand, if the solution exist for longer time, the behaviour of the solution is controlled by (5.7).
Proof. (i) Taking the Fourier transform of system (5.2), we get
where $\hat U(t) = \hat U(\xi,\, t) = \mathcal {F} U (\xi,\, t)$![]() , $B( \varepsilon,\, \xi )$
, $B( \varepsilon,\, \xi )$![]() is defined as
is defined as

Further, the eigenvalues of the matrix $B$![]() are computed from the determinant
are computed from the determinant
That is,

The corresponding eigenvectors of $B$![]() are
are
where

Then the solution of (5.9) can be represented by
and the inverse Fourier transform

gives the solution to (5.2), where

Now let us estimate each part of the above decomposition. First, by definition, we compute

where $\mathcal {G}(x,\,t) =({1}/{ 4\pi \mu t})^{d/2} \exp (- ({|x|^2}/{ 4 \mu t}))$![]() is the heat kernel. Since $e_j(\xi ) = (0,\, \tilde e_j(\xi )^T ) ^T$
is the heat kernel. Since $e_j(\xi ) = (0,\, \tilde e_j(\xi )^T ) ^T$![]() , we get
, we get
in which

that is, $P$![]() is the orthogonal projection of $H^s$
is the orthogonal projection of $H^s$![]() onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$
onto the subspace $\{v\in H^s: \, \nabla \cdot v = 0 \}$![]() . Furthermore, (5.5) is proved by using Hausdorff–Young inequality for convolution.
. Furthermore, (5.5) is proved by using Hausdorff–Young inequality for convolution.
Next, to estimate $\mathcal {L}^\varepsilon _\pm$![]() for given $\varepsilon$
for given $\varepsilon$![]() , we recall that
, we recall that
Due to the singularity of the heat kernel at $t=0$![]() and good decay away from $t=0$
and good decay away from $t=0$![]() , we need to have more precise local in time estimate of the solution operator such that the result is integrable in time. Thus we need two sets of estimates: $t<\delta$
, we need to have more precise local in time estimate of the solution operator such that the result is integrable in time. Thus we need two sets of estimates: $t<\delta$![]() and $t\geq \delta$
and $t\geq \delta$![]() , for any given positive constant $\delta$
, for any given positive constant $\delta$![]() . Without loss of generality, we take $\delta =1$
. Without loss of generality, we take $\delta =1$![]() , then derive the estimate for $t<1$
, then derive the estimate for $t<1$![]() and $t\geq 1$
and $t\geq 1$![]() , respectively. (ii) For $t<1$
, respectively. (ii) For $t<1$![]() , let
, let
the frequency is decomposed into three parts: $|\xi |^2 \in [0,\, A],\, ~ [A,\,B],\, ~[B,\, \infty )$![]() . Note that $t <1$
. Note that $t <1$![]() , the above selection of $A$
, the above selection of $A$![]() implies $A < C := {2a }/({ (\mu +\nu )^2\varepsilon ^2 })$
implies $A < C := {2a }/({ (\mu +\nu )^2\varepsilon ^2 })$![]() for $\varepsilon$
for $\varepsilon$![]() small, thus $F$
small, thus $F$![]() is strictly increasing in the low frequency part. See figure 1.
is strictly increasing in the low frequency part. See figure 1.

FIG. 1. Frequency decomposition.
Then we have
where

In the following we will give the estimates of $I_{\pm },\, J_{\pm }$![]() and $K_{\pm }$
and $K_{\pm }$![]() , respectively. First, it is easy to compute
, respectively. First, it is easy to compute

Setting

then for $k=1,\,2$![]() , we have
, we have

Note $g_{\pm, k}(0,\,x) = 0$![]() , we have
, we have

thus

Recall $A= ( \frac {t }{ \varepsilon } )^{2\theta }$![]() . Direct computation shows
. Direct computation shows

thus the first term in the right hand side of (5.14) can be controlled by

Moreover, we compute

Recall that for $d\geq 3$![]() , one has (see [Reference Ali and Chen3, P2756]),
, one has (see [Reference Ali and Chen3, P2756]),
and noting also that $\zeta (r)$![]() and $\zeta ' (r)$
and $\zeta ' (r)$![]() will both have a factor ${\rm e}^{- ({(\mu + \nu )}/{ 2}) r^2 t }$
will both have a factor ${\rm e}^{- ({(\mu + \nu )}/{ 2}) r^2 t }$![]() , after tedious calculation, with the estimates in (5.15), we find
, after tedious calculation, with the estimates in (5.15), we find
Similar estimate holds for $g_{\pm, 2} (r,\,x)$![]() . Thus for $k=1,\,2$
. Thus for $k=1,\,2$![]() ,
,

Plugging (5.16) and (5.17) into (5.14), we have

Next, since

we have

Finally, noting that $F$![]() is negative for $|\xi |^2 \geq B$
is negative for $|\xi |^2 \geq B$![]() , then $\lambda _\pm$
, then $\lambda _\pm$![]() are real numbers:
are real numbers:
where $0 < \delta = ({(4 (1+a|\xi |^2) )}/{( (\mu +\nu )^2 |\xi |^4 \varepsilon ^2)}) \leq 1$![]() in the case of high frequency. Moreover, since $\delta \in (0,\, 1]$
in the case of high frequency. Moreover, since $\delta \in (0,\, 1]$![]() ,
,
then
Hence we have

Combine (5.18), (5.19), (5.21) and (5.13), we conclude (5.6). (iii) Next, we prove (5.7) for the case $t\geq 1$![]() . Indeed, we will use different frequency decomposition. That is, taking $\tilde A = C/2 = {a }/({ (\mu +\nu )^2\varepsilon ^2 })$
. Indeed, we will use different frequency decomposition. That is, taking $\tilde A = C/2 = {a }/({ (\mu +\nu )^2\varepsilon ^2 })$![]() , the three parts of the frequency are now $|\xi |^2 \in [0,\, \tilde A],\, ~ [\tilde A,\,B],\, ~[B,\, \infty )$
, the three parts of the frequency are now $|\xi |^2 \in [0,\, \tilde A],\, ~ [\tilde A,\,B],\, ~[B,\, \infty )$![]() . The estimate (5.16) is modified to
. The estimate (5.16) is modified to
the estimate (5.17) is modified to

thus, instead of (5.18), we have

Next, for the medium frequency part, the estimate (5.19) is modified to

The high frequency part estimate is unchanged. Combining (5.21)–(5.23), we have the estimate (5.7) for $t>1$![]() . (iv) The estimate (5.8) is directly derived from (5.5)–(5.7). The proof of the lemma is finished.
. (iv) The estimate (5.8) is directly derived from (5.5)–(5.7). The proof of the lemma is finished.
Moreover, from Hölder's inequality, lemma 2.1 and the uniform estimates in theorem 1.1, we also have
Lemma 5.3 Under the assumptions of theorem 1.1, there exists a constant $C>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() such that for any $\tau \in [0,\,T_0]$
such that for any $\tau \in [0,\,T_0]$![]() , $k=1,\,2$
, $k=1,\,2$![]() ,
,
The proof of lemma 5.3 is same as that of lemma 7 in [Reference Ali and Chen3], and we can omit the details here.
Now let us consider the zero-electron-mass limit of the initial value problem (1.2)–(1.3) in the ill-prepared initial data case. First, by the Duhamel's principle, the solution of system (5.1) can be given as
where $\mathcal {L}^\varepsilon (t)$![]() is the solution operator studied in previous subsection, and
is the solution operator studied in previous subsection, and
Note the decomposition (5.3), we rewrite
where

By the definition of $\mathcal {L}^\varepsilon _* (t)$![]() and (5.4)–(5.5), we have
and (5.4)–(5.5), we have
Note (5.5) and the heat kernel $\mathcal {G}$![]() is smooth, then, with use of lemma 5.1 and lemma 5.3, we have
is smooth, then, with use of lemma 5.1 and lemma 5.3, we have
Lemma 5.4 Under the assumptions of theorem 1.3, there exists a constant $C$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() such that
such that
Proof. By the orthogonal projection, we firstly have
from the uniform estimate (1.9). Secondly, the solution $u_*^\varepsilon$![]() defined in (5.26) satisfies
defined in (5.26) satisfies
thus
by using (1.9), lemma 5.1 and lemma 5.3. The proof is completed.
Lemma 5.5 Assume $U_I \in L^1\cap H^s$![]() . For any fixed $s >0,$
. For any fixed $s >0,$![]() it holds that
it holds that
Proof. Without loss of generality, we assume $t>1$![]() and decompose the integral
and decompose the integral
By using (5.8), we find
For $\tau \in [0,\, t-1]$![]() , that is, $t- \tau \geq 1$
, that is, $t- \tau \geq 1$![]() , then using the estimate of $\mathcal {L}^\varepsilon _\pm$
, then using the estimate of $\mathcal {L}^\varepsilon _\pm$![]() in (5.7) and lemma 5.1, we compute
in (5.7) and lemma 5.1, we compute

thus we have

Similarly, for $\tau \in (t-1,\, t]$![]() , that is, $0 \leq t- \tau <1$
, that is, $0 \leq t- \tau <1$![]() , then use the estimate of $\mathcal {L}^\varepsilon _\pm$
, then use the estimate of $\mathcal {L}^\varepsilon _\pm$![]() in (5.6) and lemma 5.1, we compute
in (5.6) and lemma 5.1, we compute

thus

Combining (5.28)–(5.30), we have (5.27). This completes the proof.
Now we are ready to prove the zero-electron-mass limit of (1.2)–(1.3) for ill-prepared initial data.
Proof Proof of theorem 1.3
Let $(n^\varepsilon,\, u^\varepsilon,\, E^\varepsilon )$![]() be a classical solution defined in theorem 1.1 to (1.2)–(1.3) in $[0,\, T_0]$
be a classical solution defined in theorem 1.1 to (1.2)–(1.3) in $[0,\, T_0]$![]() , with $T_0>0$
, with $T_0>0$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() . From (1.9), we have
. From (1.9), we have
Recall (5.24)–(5.25), we write
For the first part $\mathcal {U}^\varepsilon _* = (0,\, u_*^\varepsilon )^T$![]() , by lemma 5.4, there exists a subsequence of $u_*^\varepsilon$
, by lemma 5.4, there exists a subsequence of $u_*^\varepsilon$![]() (still denoted by itself), and $u_*^0 \in C^0([0,\, T_0] \times \mathbb {R}^d) \cap L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) )$
(still denoted by itself), and $u_*^0 \in C^0([0,\, T_0] \times \mathbb {R}^d) \cap L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) )$![]() , such that
, such that
Further use lemma 5.5, we have
By the orthogonal decomposition of $\mathcal {U}^\varepsilon$![]() , we have $P u_*^\varepsilon = u_*^\varepsilon$
, we have $P u_*^\varepsilon = u_*^\varepsilon$![]() . Passing to the limit as $\varepsilon \to 0$
. Passing to the limit as $\varepsilon \to 0$![]() gives
gives
Next, recall the uniform estimates in theorem 1.1, we have the weak-$*$![]() convergence of $(\tilde n^\varepsilon,\, u^\varepsilon )$
convergence of $(\tilde n^\varepsilon,\, u^\varepsilon )$![]() in $L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) )$
in $L^\infty ( [0,\, T_0] ; H^s (\mathbb {R}^d) )$![]() , thus
, thus
Now pass to the limit as $\varepsilon \to 0$![]() in (5.26), we get
in (5.26), we get
thus $u_*^0$![]() satisfies the equation
satisfies the equation
thus the proof of theorem 1.3 is complete.
Acknowledgments
The authors would like to express sincere thanks to the referees for the suggestive comments on this paper. Li is supported in part by the National Natural Science Foundation of China (Grant No. 12171258). Liao is supported in part by the National Natural Science Foundation of China (Grant Nos. 11871335 and 11971008).