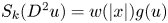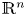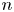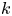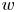1. Introduction and main results
This paper deals with the semi-stability of nonconstant radial solutions of
posed in $\mathbb {R}^n$![]() , where $n\geq 1$
, where $n\geq 1$![]() , $k\in \{1,\,\ldots,\,n\}$
, $k\in \{1,\,\ldots,\,n\}$![]() , the function $g\in C^1(\mathbb {R})$
, the function $g\in C^1(\mathbb {R})$![]() is nonnegative and nonincreasing, and $w$
is nonnegative and nonincreasing, and $w$![]() is a nonnegative radial function that satisfies some suitable conditions. The operator $S_k(D^2u)$
is a nonnegative radial function that satisfies some suitable conditions. The operator $S_k(D^2u)$![]() is the $k$
is the $k$![]() -Hessian of $u$
-Hessian of $u$![]() , which is defined by the sum of all $k$
, which is defined by the sum of all $k$![]() -th principal minors of the Hessian matrix. Alternatively, $S_k(D^2u)$
-th principal minors of the Hessian matrix. Alternatively, $S_k(D^2u)$![]() is the $k$
is the $k$![]() -th elementary symmetric polynomial of the eigenvalues of the Hessian matrix $D^2 u$
-th elementary symmetric polynomial of the eigenvalues of the Hessian matrix $D^2 u$![]() . According to [Reference Caffarelli, Nirenberg and Spruck1], to ensure ellipticity of equation (1.1), we consider $k$
. According to [Reference Caffarelli, Nirenberg and Spruck1], to ensure ellipticity of equation (1.1), we consider $k$![]() -admissible or $k$
-admissible or $k$![]() -convex solutions, i.e., functions that belong to
-convex solutions, i.e., functions that belong to
We point out that there are no previous works concerning semi-stable solutions to the $k$![]() -Hessian operator in the whole space $\mathbb {R}^n$
-Hessian operator in the whole space $\mathbb {R}^n$![]() for general nonlinearities and $k\neq 1$
for general nonlinearities and $k\neq 1$![]() . In fact, to the best of our knowledge, the only results devoted to stable solutions to (1.1) are contained in the work [Reference Wang and Lei10] and they concern only the particular cases $w(r)\equiv 1$
. In fact, to the best of our knowledge, the only results devoted to stable solutions to (1.1) are contained in the work [Reference Wang and Lei10] and they concern only the particular cases $w(r)\equiv 1$![]() and $g(u)$
and $g(u)$![]() a power nonlinearity. More precisely, in [Reference Wang and Lei10], the authors gave a definition of stable radial solutions of the $k$
a power nonlinearity. More precisely, in [Reference Wang and Lei10], the authors gave a definition of stable radial solutions of the $k$![]() -Hessian equation $F_{k}(D^2V)=(-V)^p$
-Hessian equation $F_{k}(D^2V)=(-V)^p$![]() in $\mathbb {R}^n$
in $\mathbb {R}^n$![]() , where $F_{k}(D^2V)=S_k(D^2\,V)$
, where $F_{k}(D^2V)=S_k(D^2\,V)$![]() . They stablished connections between stability and certain critical exponents of Joseph–Lundgren type available for $k$
. They stablished connections between stability and certain critical exponents of Joseph–Lundgren type available for $k$![]() -Hessian operators. Their tools also include Wolff potentials.
-Hessian operators. Their tools also include Wolff potentials.
For existence and non-existence results for equations of the form (1.1) we refer to [Reference Clément, Manásevich and Mitidieri3], where a special emphasis was put in the model equation
being
Some existence and non-existence results for radial solutions are given in terms of an integral condition involving the function $a$![]() . In [Reference Lei6], among other results, the author constructs explicit negative solutions of the equation $F_{k}(D^2V)=R(x)(-V)^q$
. In [Reference Lei6], among other results, the author constructs explicit negative solutions of the equation $F_{k}(D^2V)=R(x)(-V)^q$![]() in $\mathbb {R}^n$
in $\mathbb {R}^n$![]() , where $F_{k}(D^2V)=S_k(D^2\,V)$
, where $F_{k}(D^2V)=S_k(D^2\,V)$![]() and $R(x)$
and $R(x)$![]() is a radial function that satisfies $C^{-1}\leq R(x)\leq C$
is a radial function that satisfies $C^{-1}\leq R(x)\leq C$![]() for some constant $C>1$
for some constant $C>1$![]() . See [Reference Lei6, theorem 4.2].
. See [Reference Lei6, theorem 4.2].
Throughout this work, we identify a radial solution $u$![]() by their one variable representant, that is, $u(x) = u(r),\, \left \vert x \right \vert =r$
by their one variable representant, that is, $u(x) = u(r),\, \left \vert x \right \vert =r$![]() . At the point $x=(r,\,0,\,\ldots,\,0)$
. At the point $x=(r,\,0,\,\ldots,\,0)$![]() , the eigenvalues of $D^2 u$
, the eigenvalues of $D^2 u$![]() are $\lambda _1=u''$
are $\lambda _1=u''$![]() , which is simple, and $\lambda _2=\frac {u'}{r}$
, which is simple, and $\lambda _2=\frac {u'}{r}$![]() , which has multiplicity $n-1$
, which has multiplicity $n-1$![]() , where by abuse of notation, we write $u'$
, where by abuse of notation, we write $u'$![]() or $\partial _r u$
or $\partial _r u$![]() as the radial derivative of a radial function $u$
as the radial derivative of a radial function $u$![]() . Thus the $k$
. Thus the $k$![]() -Hessian operator acting on radially symmetric $C^2$
-Hessian operator acting on radially symmetric $C^2$![]() functions can be written as
functions can be written as
where $c_{n,k}$![]() is defined by $c_{n,k}=\binom {n}{k}/n$
is defined by $c_{n,k}=\binom {n}{k}/n$![]() .
.
Remark 1.1 Note that, if $u$![]() is a radial solution of (1.1) then, in particular, $S_1(D^2 u)=r^{1-n}(r^{n-1}u')'\geq 0$
is a radial solution of (1.1) then, in particular, $S_1(D^2 u)=r^{1-n}(r^{n-1}u')'\geq 0$![]() . Thus $G(r)=r^{n-1}u'$
. Thus $G(r)=r^{n-1}u'$![]() is nondecreasing, since ${G(0)=0}$
is nondecreasing, since ${G(0)=0}$![]() , we deduce that $G\geq 0$
, we deduce that $G\geq 0$![]() and hence $u$
and hence $u$![]() is nondecreasing. As a consequence, $\lambda _2\geq 0$
is nondecreasing. As a consequence, $\lambda _2\geq 0$![]() .
.
Definition 1.2 We say that a radial solution $u\in \Phi ^k$![]() of (1.1) is semi-stable if
of (1.1) is semi-stable if
for every radially symmetric function $\xi \in C_c^{1}(\mathbb {R}^n)$![]() .
.
In this paper, we establish pointwise estimates and necessary conditions for the existence of semi-stable solutions (not necessarily bounded) of (1.1). For bounded solutions we estimate their asymptotic behaviour at infinity. All the estimates are given in terms of the spatial dimension $n$![]() , the values of $k$
, the values of $k$![]() and the behaviour at infinity of the growth rate function of $w$
and the behaviour at infinity of the growth rate function of $w$![]() , that is, the function $W(r):=\frac {rw'(r)}{w(r)}$
, that is, the function $W(r):=\frac {rw'(r)}{w(r)}$![]() .
.
We now establish our precise assumptions on the weight $w(r)$![]() that we will assume throughout the paper:
that we will assume throughout the paper:

In order to state our main results, we need the following notation:
Let

where
Note that when $k=1$![]() and $w\equiv 1$
and $w\equiv 1$![]() , $\delta (r)$
, $\delta (r)$![]() takes the constant value $-\frac {n}{2}+\sqrt {n-1}+2$
takes the constant value $-\frac {n}{2}+\sqrt {n-1}+2$![]() , which plays a crucial role in pointwise estimates. We refer to [Reference Villegas9] by Villegas for details. A great difference here is that $\delta (r)$
, which plays a crucial role in pointwise estimates. We refer to [Reference Villegas9] by Villegas for details. A great difference here is that $\delta (r)$![]() is a variable exponent, this produces additional technical difficulties.
is a variable exponent, this produces additional technical difficulties.
Our main results are
Proposition 1.3 Let $n>k(k+1)/(2k+\gamma )$![]() and $u$
and $u$![]() be a semi-stable nonconstant radial solution of (1.1). Then $\left \vert \nabla u(x)\right \vert >0$
be a semi-stable nonconstant radial solution of (1.1). Then $\left \vert \nabla u(x)\right \vert >0$![]() for all $\left \vert x \right \vert >0$
for all $\left \vert x \right \vert >0$![]() .
.
We have the following pointwise estimate for not necessarily bounded solutions of (1.1).
Theorem 1.4 Let $w\in C^1(\mathbb {R}^n{\setminus} \{0\})$![]() be a radial function that satisfies (1.4) , $n>k(k+1)/(2k+\gamma )$
be a radial function that satisfies (1.4) , $n>k(k+1)/(2k+\gamma )$![]() and $u$
and $u$![]() be a semi-stable nonconstant radial solution of (1.1) (not necessarily bounded). Then, there exist $M>0$
be a semi-stable nonconstant radial solution of (1.1) (not necessarily bounded). Then, there exist $M>0$![]() and $r_0\geq 1$
and $r_0\geq 1$![]() depending on $u$
depending on $u$![]() and $w$
and $w$![]() such that for all $r\geq r_0$
such that for all $r\geq r_0$![]() ,
,

Remark 1.5 This theorem is sharp for some $\beta \in \mathbb {R},\, \mu =\frac {\sigma }{k}+2$![]() and
and

where $\sigma >-k$![]() and $w(r)=r^{\sigma }$
and $w(r)=r^{\sigma }$![]() , as shown in the appendix.
, as shown in the appendix.
Theorem 1.6 Let $w\in C^1(\mathbb {R}^n{\setminus} \{0\})$![]() be a radial function that satisfies (1.4), $n\geq 2$
be a radial function that satisfies (1.4), $n\geq 2$![]() and $u$
and $u$![]() be a semi-stable nonconstant bounded radial solution of (1.1). Then,
be a semi-stable nonconstant bounded radial solution of (1.1). Then,
(i) $n>2(k+\frac {2\gamma }{k}+4)$
 .
.(ii) There exists $u_\infty =\lim \limits _{r\rightarrow +\infty }{u(r)}\in \mathbb {R}$
 and $M>0$
and $M>0$ depending on $u$
depending on $u$ and $w$
and $w$ such that for all $r\geq 1,$
such that for all $r\geq 1,$ (1.9)\begin{equation} \left\vert u(r)-u_\infty\right\vert \geq M r^{\delta(r)}. \end{equation}
(1.9)\begin{equation} \left\vert u(r)-u_\infty\right\vert \geq M r^{\delta(r)}. \end{equation}
Remark 1.8 See [Reference Villegas9] to compare our results with the semilinear case ($k=1$![]() ) and for related equations involving the $p$
) and for related equations involving the $p$![]() -Laplacian operator, see [Reference Castorina, Esposito and Sciunzi2, Reference Fazly5, Reference Navarro and Villegas8].
-Laplacian operator, see [Reference Castorina, Esposito and Sciunzi2, Reference Fazly5, Reference Navarro and Villegas8].
This paper is organized as follows. In § 2 we prove our main results, proposition 1.3, theorem 1.4 and theorem 1.6. We conclude the paper by presenting in the appendix some examples of functions $w$![]() and $g$
and $g$![]() for which our theorems are sharp.
for which our theorems are sharp.
2. Proof of the main results
We claim that if $u$![]() is a $C^2$
is a $C^2$![]() radial solution, then $u'\in C_{loc}^{0,1}(\mathbb {R}^n)$
radial solution, then $u'\in C_{loc}^{0,1}(\mathbb {R}^n)$![]() . To prove our claim, we first observe that $u'\in C^0(\mathbb {R}^n)\cap C^1(\mathbb {R}^n{\setminus} \{0\})$
. To prove our claim, we first observe that $u'\in C^0(\mathbb {R}^n)\cap C^1(\mathbb {R}^n{\setminus} \{0\})$![]() with $u'(0)=0$
with $u'(0)=0$![]() and $\left \vert u '(x)\right \vert \leq C_R\left \vert x \right \vert$
and $\left \vert u '(x)\right \vert \leq C_R\left \vert x \right \vert$![]() in any open ball $B_R$
in any open ball $B_R$![]() of radius $R>0$
of radius $R>0$![]() . Now from (1.1) and (1.2) we obtain, for $r>0$
. Now from (1.1) and (1.2) we obtain, for $r>0$![]() ,
,
from which we deduce that

Thus, for any $R>0$![]() , the function $u''$
, the function $u''$![]() is bounded on $B_R{\setminus} \{0\}$
is bounded on $B_R{\setminus} \{0\}$![]() . Also for any $x,\,y\in \mathbb {R}^n$
. Also for any $x,\,y\in \mathbb {R}^n$![]() such that $R>\left \vert y \right \vert >\left \vert x \right \vert >0$
such that $R>\left \vert y \right \vert >\left \vert x \right \vert >0$![]() , we have
, we have

We conclude that $u'\in C_{loc}^{0,1}(\mathbb {R}^n)$![]() . This will be used in the proof of lemma 2.1 below.
. This will be used in the proof of lemma 2.1 below.
Lemma 2.1 Let $n\geq 2$![]() and $u$
and $u$![]() be any radial solution of (1.1). Then
be any radial solution of (1.1). Then

for every radially symmetric function $\eta \in (H_c^1\cap L_{loc}^{\infty })(\mathbb {R}^n)$![]() , where $v$
, where $v$![]() is defined as in (1.7). Here $(\cdot,\, \cdot )$
is defined as in (1.7). Here $(\cdot,\, \cdot )$![]() denotes the standard scalar product in $\mathbb {R}^n$
denotes the standard scalar product in $\mathbb {R}^n$![]() .
.
Proof. Let $\eta \in H_c^1(\mathbb {R}^n)\cap L_{loc}^\infty (\mathbb {R}^n)$![]() and $\zeta \in C_{loc}^{0,1}(\mathbb {R}^n)$
and $\zeta \in C_{loc}^{0,1}(\mathbb {R}^n)$![]() be radial functions. Then, by a standard density argument, we can take $\xi =\zeta \eta \in H_c^1(\mathbb {R}^n)\cap L_{loc}^\infty (\mathbb {R}^n)$
be radial functions. Then, by a standard density argument, we can take $\xi =\zeta \eta \in H_c^1(\mathbb {R}^n)\cap L_{loc}^\infty (\mathbb {R}^n)$![]() in (1.3) to obtain
in (1.3) to obtain

Thus, as $u$![]() and $\zeta$
and $\zeta$![]() are radial functions, we get
are radial functions, we get

where $\lambda _2=u'/{\left \vert x \right \vert }$![]() .
.
From (1.2) and differentiating (1.1) with respect to $r$![]() , we obtain
, we obtain

Then, multiplying the latter equation by $u'\eta ^2=r\lambda _2\eta ^2$![]() , we have
, we have

Thus, integrating by parts, and taking into account that $\lambda _2\in L_{loc}^\infty (\mathbb {R}^n)$![]() , we obtain
, we obtain

and

Next, using $\zeta =u'$![]() in (2.2), (2.3), we have
in (2.2), (2.3), we have

Then, from (2.2), (2.4), (2.5), (2.6) and (2.7), we obtain

Since
from (1.7), we have
Hence

which concludes the proof.
Multiplying the equation (1.2) by $r^{n+\frac {n}{k}-1}\lambda _2$![]() , we obtain
, we obtain
Since $r\lambda _2=u'$![]() , the above equation is equivalent to
, the above equation is equivalent to
On the other hand, from (1.4) and (1.7), we have
Thus, if $n>k(k+1)/(2k+\gamma )$![]() , it follows that
, it follows that
Proof of proposition 1.3. We follow an argument similar to that of proposition 1 in [Reference Farina and Navarro4]. Let $n>k(k+1)/(2k+\gamma )$![]() and let $u$
and let $u$![]() be a semi-stable nonconstant radial solution of (1.1). Arguing by contradiction, assume that $u'(r_0) = 0$
be a semi-stable nonconstant radial solution of (1.1). Arguing by contradiction, assume that $u'(r_0) = 0$![]() for some $r_0 > 0$
for some $r_0 > 0$![]() . Now let $\chi _{B_{r_0}}$
. Now let $\chi _{B_{r_0}}$![]() be the indicator function of the open ball of radius $r_0$
be the indicator function of the open ball of radius $r_0$![]() centred at the origin, so $\chi _{B_{r_0}}\in H_c^1(\mathbb {R}^n)\cap L_{loc}^\infty (\mathbb {R}^n)$
centred at the origin, so $\chi _{B_{r_0}}\in H_c^1(\mathbb {R}^n)\cap L_{loc}^\infty (\mathbb {R}^n)$![]() . From (2.1), we obtain
. From (2.1), we obtain

where we have used the fact that $\lambda _2\geq 0$![]() , (2.10) and the monotonicity of $v$
, (2.10) and the monotonicity of $v$![]() to get the above inequality. Thus, the semi-stability of $u$
to get the above inequality. Thus, the semi-stability of $u$![]() implies that $u(r)=u_0$
implies that $u(r)=u_0$![]() for all $r\in [0,\,r_0]$
for all $r\in [0,\,r_0]$![]() .
.
Let $v(r)=(r^{\frac {n}{k}-1}u')^{k+1}$![]() . From (2.8), we have the following problem
. From (2.8), we have the following problem

Finally, by Cauchy's theorem, we get that $u=u_0$![]() for any $r>0$
for any $r>0$![]() , a contradiction.
, a contradiction.
We adapt some estimates given by Villegas in [Reference Villegas9] for the nonweighted semilinear equation. Here is one of our main integral estimates.
Lemma 2.2 Let $w\in C^1(\mathbb {R}^n{\setminus} \{0\})$![]() be a radial function that satisfies (1.4) , ${n>k(k+1)/ (2k+\gamma)}$
be a radial function that satisfies (1.4) , ${n>k(k+1)/ (2k+\gamma)}$![]() and $u$
and $u$![]() be a semi-stable nonconstant radial solution of (1.1). Then, there exists $K>0$
be a semi-stable nonconstant radial solution of (1.1). Then, there exists $K>0$![]() depending on $u$
depending on $u$![]() and $w$
and $w$![]() and such that
and such that
Proof. From proposition 1.3, we have that $u'(r)\neq 0$![]() for all $r>0$
for all $r>0$![]() . Furthermore, $u'>0$
. Furthermore, $u'>0$![]() on $(0,\,\infty )$
on $(0,\,\infty )$![]() (see remark 1.1).
(see remark 1.1).
Next we show that $\alpha (r)$![]() defined in (1.5) is strictly positive for all $r\geq 1$
defined in (1.5) is strictly positive for all $r\geq 1$![]() . For this, let $\kappa \geq 0$
. For this, let $\kappa \geq 0$![]() and define the function
and define the function
From (2.10), we have
Then

Thus, from (1.4), (2.10), (2.12) and (2.13), we obtain
and

Therefore by the previous inequalities, we get

We now fix $R>r\geq 1$![]() and consider the function
and consider the function

Since, $u$![]() is a semi-stable solution, from (2.1), we have
is a semi-stable solution, from (2.1), we have

where $\omega _n$![]() is the measure area of the $n-1$
is the measure area of the $n-1$![]() dimensional unit sphere $S^{n-1}$
dimensional unit sphere $S^{n-1}$![]() .
.
Then by (2.10), we have

and by (1.5), we obtain

Now to estimate $I_3$![]() , we need to consider two cases according to the sign of $v$
, we need to consider two cases according to the sign of $v$![]() in the interval $[r,\,R]$
in the interval $[r,\,R]$![]() . For this, we rewrite $I_3$
. For this, we rewrite $I_3$![]() as
as
and we define $\Phi _R: [r,\,R]\rightarrow \mathbb {R}$![]() as
as
and recall that $\lambda _2=u'(s)/s$![]() for $s>0$
for $s>0$![]() .
.
Thus for $t\in [r,\,R]$![]() :
:
• If $v(t)\geq 0$
 , then by (2.10), it follows that
(2.19)\begin{equation} \begin{aligned} I_3^+ & =\int_r^R{t^{n-1}\lambda_{2}^{k+1}\left((t\eta')^2+2v(t)(t\eta\eta')\right)\,{\rm d}t}\\ & \quad-\int_r^R{t^{n-1}\lambda_{2}^{k+1}\left(\left(\frac{n}{k}v(t)+\frac{n}{k}-1-tv'(t)\right)\eta^2\right)\,{\rm d}t}\\ & \leq\int_r^R{t^{n-1}\lambda_{2}^{k+1}\frac{r^{{-}2\alpha(r)}}{\Phi^2_{R}(r)}t^{{-}2n}\lambda_{2}^{{-}2(k+1)}\,{\rm d}t}\\ & =\frac{r^{{-}2\alpha(r)}}{\Phi^2_{R}(r)}\int_{r}^R t^{-(n+1)}\lambda_2^{-(k+1)}\,{\rm d}t=\frac{r^{{-}2\alpha(r)}}{\Phi_{R}(r)}. \end{aligned} \end{equation}
, then by (2.10), it follows that
(2.19)\begin{equation} \begin{aligned} I_3^+ & =\int_r^R{t^{n-1}\lambda_{2}^{k+1}\left((t\eta')^2+2v(t)(t\eta\eta')\right)\,{\rm d}t}\\ & \quad-\int_r^R{t^{n-1}\lambda_{2}^{k+1}\left(\left(\frac{n}{k}v(t)+\frac{n}{k}-1-tv'(t)\right)\eta^2\right)\,{\rm d}t}\\ & \leq\int_r^R{t^{n-1}\lambda_{2}^{k+1}\frac{r^{{-}2\alpha(r)}}{\Phi^2_{R}(r)}t^{{-}2n}\lambda_{2}^{{-}2(k+1)}\,{\rm d}t}\\ & =\frac{r^{{-}2\alpha(r)}}{\Phi^2_{R}(r)}\int_{r}^R t^{-(n+1)}\lambda_2^{-(k+1)}\,{\rm d}t=\frac{r^{{-}2\alpha(r)}}{\Phi_{R}(r)}. \end{aligned} \end{equation}
• If $v(t)<0$
 , then for all $\epsilon >0$
, then for all $\epsilon >0$ \[{-}2v(t)\Phi_R(t)t^{{-}n}\lambda_2^{-(k+1)}\leq \epsilon^2v(t)^2\Phi_R(t)^2+\frac{t^{{-}2n}\lambda_2^{{-}2(k+1)}}{\epsilon^2}, \]and
\[{-}2v(t)\Phi_R(t)t^{{-}n}\lambda_2^{-(k+1)}\leq \epsilon^2v(t)^2\Phi_R(t)^2+\frac{t^{{-}2n}\lambda_2^{{-}2(k+1)}}{\epsilon^2}, \]and \begin{align*} I_3^{-}& \leq \left(1+\frac1{\epsilon^2}\right) \frac{r^{{-}2\alpha(r)}}{\Phi_R(r)}-\frac{r^{{-}2\alpha(r)}}{\Phi_R(r)^2}\\ & \quad\times\int_{\{t\in[r,R]:v(t)<0\}}{t^{n-1}\lambda_2^{k+1}\left( \!-\epsilon^2v(t)^2\!+\!\frac{n}{k}v(t)\!+\frac{n}{k}-1\!-\!tv'(t)\right)\Phi_R(t)^2\,{\rm d}t }. \end{align*}
\begin{align*} I_3^{-}& \leq \left(1+\frac1{\epsilon^2}\right) \frac{r^{{-}2\alpha(r)}}{\Phi_R(r)}-\frac{r^{{-}2\alpha(r)}}{\Phi_R(r)^2}\\ & \quad\times\int_{\{t\in[r,R]:v(t)<0\}}{t^{n-1}\lambda_2^{k+1}\left( \!-\epsilon^2v(t)^2\!+\!\frac{n}{k}v(t)\!+\frac{n}{k}-1\!-\!tv'(t)\right)\Phi_R(t)^2\,{\rm d}t }. \end{align*}
Moreover, by (1.4) and (1.7), we have that
\[ \left\vert v_{\infty}\right\vert>\left\vert v(t)\right\vert>0\mbox{ for any }t\in\{t\in[r,R]:v(t)<0\}. \]
By (2.10) we can pick $\epsilon \in (0,\,\sqrt {\frac {n}{k}v_{\infty }+\frac {n}{k}-1}/\left \vert v _{\infty }\right \vert )$
 . Then applying the Young's inequality with $\varepsilon$
. Then applying the Young's inequality with $\varepsilon$ to $-v(t)\Phi _R(t) t^{-n}\lambda _2^{-(k+1)}$
to $-v(t)\Phi _R(t) t^{-n}\lambda _2^{-(k+1)}$ with exponents 2 and 2, and using again (2.10), we have
\[ -\epsilon^2v(t)^2+\frac{n}{k}v(t)+\frac{n}{k}-1-tv'(t)\geq{-}\epsilon^2v_{\infty}^2+\frac{n}{k}v_{\infty}+\frac{n}{k}-1>0, \]and therefore
with exponents 2 and 2, and using again (2.10), we have
\[ -\epsilon^2v(t)^2+\frac{n}{k}v(t)+\frac{n}{k}-1-tv'(t)\geq{-}\epsilon^2v_{\infty}^2+\frac{n}{k}v_{\infty}+\frac{n}{k}-1>0, \]and therefore (2.20)\begin{equation} I_3^{-}\leq\left(1+\frac{1}{\epsilon^2}\right) \frac{r^{{-}2\alpha(r)}}{\Phi_R(r)}. \end{equation}
(2.20)\begin{equation} I_3^{-}\leq\left(1+\frac{1}{\epsilon^2}\right) \frac{r^{{-}2\alpha(r)}}{\Phi_R(r)}. \end{equation}
Finally, from (2.15)–(2.17), (2.19) and (2.20), the lemma follows.
Applying lemma 2.2 enables us to prove the following pointwise estimate.
Proposition 2.3 Let $w\in C^1(\mathbb {R}^n{\setminus} \{0\})$![]() be a radial function that satisfies (1.4) , $n>k(k+1)/(2k+\gamma )$
be a radial function that satisfies (1.4) , $n>k(k+1)/(2k+\gamma )$![]() and $u$
and $u$![]() be a semi-stable nonconstant radial solution of (1.1). Then, there exists $K'>0$
be a semi-stable nonconstant radial solution of (1.1). Then, there exists $K'>0$![]() depending on $u$
depending on $u$![]() and $w$
and $w$![]() and such that
and such that
Proof. Fix $r\geq 1$![]() . Applying Hölder's inequality, lemma 2.2 with $R=2r$
. Applying Hölder's inequality, lemma 2.2 with $R=2r$![]() and recalling that $u'$
and recalling that $u'$![]() does not vanish in $(0,\,\infty )$
does not vanish in $(0,\,\infty )$![]() , we deduce
, we deduce

which gives (2.21).
Proof of theorem 1.4. Let $\delta (r)$![]() and $\delta _\infty (\gamma )$
and $\delta _\infty (\gamma )$![]() as in (1.6). By (2.9) and (2.10), we obtain
as in (1.6). By (2.9) and (2.10), we obtain
Thus, from (1.4), (1.5), (1.7), the L'Höspital rule and the elementary equality $2\sqrt {ab}=a+b-(\sqrt {a}-\sqrt {b})^2$![]() for $a,\,b\geq 0$
for $a,\,b\geq 0$![]() , we have
, we have

where $C$![]() is a positive constant depending on $n,\,k$
is a positive constant depending on $n,\,k$![]() and $\gamma$
and $\gamma$![]() .
.
Additionally, from (2.14) and (1.6), we obtain
Now, according to the dimension $n$![]() , we consider three cases:
, we consider three cases:
• Case $n>2(k+\frac {2\gamma }{k}+4)$
 . By (2.22), $\delta _{\infty }(\gamma )<0$
. By (2.22), $\delta _{\infty }(\gamma )<0$ , and by continuity there exists $r_0>1$
, and by continuity there exists $r_0>1$ such that $\delta (r)<0$
such that $\delta (r)<0$ for any $r\geq r_0$
for any $r\geq r_0$ . At this point, we have two subcases:
. At this point, we have two subcases:• $\lim \limits _{r\to +\infty }{\left \vert u (r)\right \vert }\in (0,\,\infty ]$
 . From (2.23), we have $0>\delta (r)\geq \delta _{\infty }(\gamma )$
. From (2.23), we have $0>\delta (r)\geq \delta _{\infty }(\gamma )$ for any $r\geq r_0$
for any $r\geq r_0$ . Then, $1>r^{\delta (r)}\geq r^{\delta _{\infty }(\gamma )}$
. Then, $1>r^{\delta (r)}\geq r^{\delta _{\infty }(\gamma )}$ , $\forall r\geq r_0$
, $\forall r\geq r_0$ and it follows that
\[ \lim\limits_{r\to +\infty}r^{\delta(r)}\in[0,1]. \]If $\lim \limits _{r\to +\infty }r^{\delta (r)}\in (0,\,1]$
and it follows that
\[ \lim\limits_{r\to +\infty}r^{\delta(r)}\in[0,1]. \]If $\lim \limits _{r\to +\infty }r^{\delta (r)}\in (0,\,1]$
 , we have a contradiction. Hence, $\lim \limits _{r\to +\infty }r^{\delta (r)}=0$
, we have a contradiction. Hence, $\lim \limits _{r\to +\infty }r^{\delta (r)}=0$ and (1.8) follows immediately.
and (1.8) follows immediately.• $\lim \limits _{r\to +\infty }{\left \vert u (r)\right \vert }=0$
 . Let $R\geq 2r$
. Let $R\geq 2r$ and $r\geq 1$
and $r\geq 1$ . Thus, by the monotony of $u$
. Thus, by the monotony of $u$ and proposition 2.3 there exists $K'>0$
and proposition 2.3 there exists $K'>0$ such that:
(2.24)\begin{equation} \begin{aligned} \left\vert u(R)-u(r)\right\vert & =\left\vert u(R)-u(2r)\right\vert+\left\vert u(2r)-u(r)\right\vert\\ & \geq\left\vert u(2r)-u(r)\right\vert\geq K'r^{\delta(r)}. \end{aligned} \end{equation}Letting $R\to +\infty$
such that:
(2.24)\begin{equation} \begin{aligned} \left\vert u(R)-u(r)\right\vert & =\left\vert u(R)-u(2r)\right\vert+\left\vert u(2r)-u(r)\right\vert\\ & \geq\left\vert u(2r)-u(r)\right\vert\geq K'r^{\delta(r)}. \end{aligned} \end{equation}Letting $R\to +\infty$
 , (1.8) is proved for $r_0=1$
, (1.8) is proved for $r_0=1$ .
.
• Case $n<2(k+\frac {2\gamma }{k}+4)$
 . We have three subcases:
. We have three subcases:
• $\lim \limits _{r\to +\infty }{\left \vert u (r)\right \vert r ^{-\delta (r)}}=0$
 . From (2.21), we have that $K'=0$
. From (2.21), we have that $K'=0$ , a contradiction.
, a contradiction.• $\lim \limits _{r\to +\infty }{\left \vert u (r)\right \vert r ^{-\delta (r)}}=L\in (0,\,+\infty )$
 . Then, $\forall \epsilon >0$
. Then, $\forall \epsilon >0$ there exists $r_0\geq 1$
there exists $r_0\geq 1$ such that $\left \vert \left \vert u (r)\right \vert r ^{-\delta (r)}-L\right \vert <\epsilon$
such that $\left \vert \left \vert u (r)\right \vert r ^{-\delta (r)}-L\right \vert <\epsilon$ for any $r\geq r_0$
for any $r\geq r_0$ and (1.8) is proved for $r_0$
and (1.8) is proved for $r_0$ .
.• $\lim \limits _{r\to +\infty }{\left \vert u (r)\right \vert r ^{-\delta (r)}}=+\infty$
 . Then there exists $r_0\geq 1$
. Then there exists $r_0\geq 1$ and $K>0$
and $K>0$ such that $\left \vert u (r)\right \vert r ^{-\delta (r)}\geq K$
such that $\left \vert u (r)\right \vert r ^{-\delta (r)}\geq K$ for any $r\geq r_0$
for any $r\geq r_0$ and (1.8) is proved for $r_0$
and (1.8) is proved for $r_0$ .
.
• Case $n=2(k+\frac {2\gamma }{k}+4)$
 . Let $r\geq 1$
. Let $r\geq 1$ . Then there exists $m\in \mathbb {N}$
. Then there exists $m\in \mathbb {N}$ and $1\leq r_1<2$
and $1\leq r_1<2$ such that $r=2^{m-1}r_1$
such that $r=2^{m-1}r_1$ . Thus, by the monotony of $u$
. Thus, by the monotony of $u$ and proposition 2.3, it follows that
(2.25)\begin{equation} \begin{aligned} \left\vert u(r)\right\vert & \geq\left\vert u(r)-u(r_1)\right\vert-\left\vert u(r_1)\right\vert\\ & =\sum_{j=1}^{m-1}\left\vert u(2^j r_1)-u(2^{j-1} r_1)\right\vert-\left\vert u(r_1)\right\vert\\ & \geq \sum_{j=1}^{m-1}{K'(2^{j-1}r_1)^{\delta(2^{j-1}r_1)}}-\left\vert u(r_1)\right\vert. \end{aligned} \end{equation}
and proposition 2.3, it follows that
(2.25)\begin{equation} \begin{aligned} \left\vert u(r)\right\vert & \geq\left\vert u(r)-u(r_1)\right\vert-\left\vert u(r_1)\right\vert\\ & =\sum_{j=1}^{m-1}\left\vert u(2^j r_1)-u(2^{j-1} r_1)\right\vert-\left\vert u(r_1)\right\vert\\ & \geq \sum_{j=1}^{m-1}{K'(2^{j-1}r_1)^{\delta(2^{j-1}r_1)}}-\left\vert u(r_1)\right\vert. \end{aligned} \end{equation}
By (2.23), we have
\[ \left(2^{j-1}r_1\right)^{\delta(2^{j-1}r_1)}\geq\left(2^{j-1}r_1\right)^{\delta_{\infty}(\gamma)}=1, \]for any $j\in \{1,\,\ldots,\,m-1\}$
 and together with (2.25), we get
(2.26)\begin{equation} \left\vert u(r)\right\vert\geq K'(m-1)-\left\vert u(r_1)\right\vert=\left(\frac{K'}{\log 2}\right)\left(\log r-\log r_1\right) -\left\vert u(r_1)\right\vert, \end{equation}and (1.8) follows easily.
and together with (2.25), we get
(2.26)\begin{equation} \left\vert u(r)\right\vert\geq K'(m-1)-\left\vert u(r_1)\right\vert=\left(\frac{K'}{\log 2}\right)\left(\log r-\log r_1\right) -\left\vert u(r_1)\right\vert, \end{equation}and (1.8) follows easily.
Proof of theorem 1.6. From (1.8) of theorem 1.4, it follows that $n\neq 2(k+\frac {2\gamma }{k}+4)$![]() .
.
Recall that
Let $R\geq 2r$![]() and $r\geq 1$
and $r\geq 1$![]() . From (2.23) and (2.24), we have
. From (2.23) and (2.24), we have
Thus, letting $r\to +\infty$![]() , we conclude that $\delta _{\infty }(\gamma )$
, we conclude that $\delta _{\infty }(\gamma )$![]() must be negative, which is equivalent to $n>2(k+\tfrac {2\gamma }{k}+4)$
must be negative, which is equivalent to $n>2(k+\tfrac {2\gamma }{k}+4)$![]() . This prove $i)$
. This prove $i)$![]() .
.
Finally, letting $R\to +\infty$![]() , we have
, we have
which is $ii)$![]() with $M=K'$
with $M=K'$![]() . The proof is complete.
. The proof is complete.
Acknowledgments
The authors express their gratitude to the referee who read the paper very carefully and made some suggestions for improving the presentation. M. Navarro was supported by XUNTA de Galicia under Grant Axudas á etapa de formación posdoutoral 2017 and partially supported by AEI of Spain under Grant MTM2016-75140-P and co-financed by European Community fund FEDER and XUNTA de Galicia under grants GRC2015/004, R2016/022 and ED431C2019/02. J. Sánchez was partially supported by ANID Fondecyt Grant No. 1221928.
Appendix A. Proofs of remarks 1.5 and 1.7
We will see that the results obtained in the previous section are optimal.
Example A.1 Let $\sigma _1,\,\sigma _2,\,\tau,\,\mu \in \mathbb {R}$![]() , $(n\geq 2)\in \mathbb {N}$
, $(n\geq 2)\in \mathbb {N}$![]() and $k\in \{1,\,2,\,\ldots,\,n\}$
and $k\in \{1,\,2,\,\ldots,\,n\}$![]() . Define the function
. Define the function
and
We assume that $\sigma _1,\,\sigma _2,\,\tau$![]() and $n$
and $n$![]() satisfy the following conditions:
satisfy the following conditions:
• If $\tau =0$
 , then
(A.3)\begin{equation} \sigma_1>{-}k\mbox{ and }\,n>\frac{k(k+1)}{2k+\sigma_1}. \end{equation}
, then
(A.3)\begin{equation} \sigma_1>{-}k\mbox{ and }\,n>\frac{k(k+1)}{2k+\sigma_1}. \end{equation}
• If $\tau >0$
 , then
(A.4)\begin{equation} \begin{aligned} & k(\sigma_2-2)\geq \sigma_1>{-}k,\,2k+\sigma_1>\tau\mbox{ and }\\ & n>\max\left\lbrace \sqrt{\frac{\tau\sigma_2}{k+1}}+\frac{2k-(k-1)\sigma_1}{k},\,\frac{k(k+1)}{2k+\sigma_1-\tau}\right\rbrace. \end{aligned} \end{equation}
, then
(A.4)\begin{equation} \begin{aligned} & k(\sigma_2-2)\geq \sigma_1>{-}k,\,2k+\sigma_1>\tau\mbox{ and }\\ & n>\max\left\lbrace \sqrt{\frac{\tau\sigma_2}{k+1}}+\frac{2k-(k-1)\sigma_1}{k},\,\frac{k(k+1)}{2k+\sigma_1-\tau}\right\rbrace. \end{aligned} \end{equation}
Now, let $u_{\beta }$![]() be a radial function defined by
be a radial function defined by

On the other hand, let $\beta \in \mathbb {R}$![]() such that
such that

where $\nu :=\sqrt {v(0)^2+\frac {n}{k}v(0)+\frac {n}{k}-1 -v'(1)}$![]() and $v$
and $v$![]() is defined by (1.7).
is defined by (1.7).
Then $u_{\beta }$![]() is a semi-stable nonconstant radial solution of (1.1) with $g=g_{\beta }$
is a semi-stable nonconstant radial solution of (1.1) with $g=g_{\beta }$![]() defined by
defined by
• If $\beta \neq 0$
 ,
\[ g_{\beta}(s):=c_{n,k} \begin{cases} \left\vert\beta\right\vert^k\left(\left(\left\vert s\right\vert^{\frac{\mu}{\beta}}-1\right)^{\frac{\sigma_2}{\mu}}+1\right)^{\frac{\tau}{\sigma_2}}\times & \mbox{if }s\in I_{\beta\neq0},\\ \times\left(n+k(\beta-2)+k\left(\mu-\beta\right)\left\vert s\right\vert^{-\frac{\mu}{\beta}}\right)\left\vert s\right\vert^{k-\frac{k\mu}{\beta}}\\ C^1-\mbox{extension} & \mbox{if }s\not\in I_{\beta\neq0}, \end{cases} \]
,
\[ g_{\beta}(s):=c_{n,k} \begin{cases} \left\vert\beta\right\vert^k\left(\left(\left\vert s\right\vert^{\frac{\mu}{\beta}}-1\right)^{\frac{\sigma_2}{\mu}}+1\right)^{\frac{\tau}{\sigma_2}}\times & \mbox{if }s\in I_{\beta\neq0},\\ \times\left(n+k(\beta-2)+k\left(\mu-\beta\right)\left\vert s\right\vert^{-\frac{\mu}{\beta}}\right)\left\vert s\right\vert^{k-\frac{k\mu}{\beta}}\\ C^1-\mbox{extension} & \mbox{if }s\not\in I_{\beta\neq0}, \end{cases} \]
• If $\beta =0$
 ,
\[ g_{0}(s):=c_{n,k} \begin{cases} \left(\left(e^{\mu s}-1\right)^{\frac{\sigma_2}{\mu}}+1\right)^{\frac{\tau}{\sigma_2}}\left(n+k(\beta-2)+k\mu e^{-\mu s}\right)e^{{-}k\mu s} & \mbox{if }s\in I_{0},\\ C^1-\mbox{extension} & \mbox{if }s\not\in I_{0}, \end{cases} \]
,
\[ g_{0}(s):=c_{n,k} \begin{cases} \left(\left(e^{\mu s}-1\right)^{\frac{\sigma_2}{\mu}}+1\right)^{\frac{\tau}{\sigma_2}}\left(n+k(\beta-2)+k\mu e^{-\mu s}\right)e^{{-}k\mu s} & \mbox{if }s\in I_{0},\\ C^1-\mbox{extension} & \mbox{if }s\not\in I_{0}, \end{cases} \]
where

To establish the above result we need the following auxiliary lemmata.
Lemma A.2 Let $\theta \in \mathbb {R}$![]() and $\rho \in C(\mathbb {R}^n),\,0\leq V\in C^1(\mathbb {R}^n{\setminus} \{0\})$
and $\rho \in C(\mathbb {R}^n),\,0\leq V\in C^1(\mathbb {R}^n{\setminus} \{0\})$![]() be radial functions such that
be radial functions such that
and
Then
for every radially symmetric function $\eta \in C^1_c(\mathbb {R}^n)$![]() .
.
Proof. Let $\eta \in C_c^{1}(\mathbb {R}^n)$![]() be a radial function, then
be a radial function, then
for all $t\in \mathbb {R}$![]() . Extending the above expression, we get the following quadratic inequality for $t$
. Extending the above expression, we get the following quadratic inequality for $t$![]() :
:

Integrating by parts and using (A.8), we obtain

Therefore, the above quadratic inequality is equivalent to

We are now ready to establish example A.1.
Proof of example A.1. We claim that $2k+\gamma >0$![]() , where $\gamma$
, where $\gamma$![]() is given in (1.4). To this end, let $w(r)$
is given in (1.4). To this end, let $w(r)$![]() as in (A.1). Then, differentiating $\log w(r)=\sigma _1\log r-\frac {\tau }{\sigma _2}\log (1+r^{\sigma _2})$
as in (A.1). Then, differentiating $\log w(r)=\sigma _1\log r-\frac {\tau }{\sigma _2}\log (1+r^{\sigma _2})$![]() with respect to $r$
with respect to $r$![]() , we obtain
, we obtain
where
It follows that
From (1.7), we have
with
Moreover, we also obtain that
On the other hand, by (A.12) we get
which, by (A.3) and (A.4), implies that
and the claim follows.
Next, we divide the proof into two steps.
Step 1. For any $\beta \in \mathbb {R}$![]() , $u_{\beta }$
, $u_{\beta }$![]() is a $k$
is a $k$![]() -convex solution of (1.1) with $g=g_{\beta }$
-convex solution of (1.1) with $g=g_{\beta }$![]() and $w$
and $w$![]() defined by (A.1).
defined by (A.1).
A direct calculation gives that

By (A.2)–(A.4), it follows that
also

Consequently, differentiating $\log \lambda _{2,\beta }$![]() with respect to $r$
with respect to $r$![]() and using (A.10), we obtain
and using (A.10), we obtain
Fix any $j\in \{1,\,2,\,\ldots,\,k\}$![]() . By (1.2), we have
. By (1.2), we have

Combining (2.12), (A.3), (A.4) and (A.12), we have

By (A.10) and setting $\lambda =\sigma _2$![]() in (A.11) together with (A.13), we get
in (A.11) together with (A.13), we get
From the last two inequalities and (2.10), (A.3), (A.4), and the fact that $-rv'(r)\geq 0$![]() for any $r\geq 0$
for any $r\geq 0$![]() , a straightforward calculation gives
, a straightforward calculation gives

From the previous inequality, (A.2) and (A.5), we deduce that

Therefore, from (A.18), $S_j(D^2 u_{\beta })\geq 0$![]() for any $j\in \{1,\,2,\,\ldots,\,k\}$
for any $j\in \{1,\,2,\,\ldots,\,k\}$![]() . This shows that the functions $u_\beta$
. This shows that the functions $u_\beta$![]() are $k$
are $k$![]() -convex.
-convex.
From (A.16) and (A.18), we have

On the other hand, it is easy to see that

From this, (A.1) and (A.2), we have

Now for every $s\geq 0$![]() , let us define the function
, let us define the function

with

which lead us to

Let $y\in I_{\beta }$![]() and $s=\left \vert y \right \vert$
and $s=\left \vert y \right \vert$![]() . Using (A.6), we see that:
. Using (A.6), we see that:
• If $\beta >0$
 , then $s\geq 1$
, then $s\geq 1$ .
.• If $\beta =0$
 , then $s\geq 0$
, then $s\geq 0$ .
.• If $\beta <0$
 , then $s\in (0,\,1]$
, then $s\in (0,\,1]$ .
.
Therefore, to study the differentiability of $f_{\beta }$![]() , we must consider the points $s=0$
, we must consider the points $s=0$![]() for $\beta \leq 0$
for $\beta \leq 0$![]() and $s=1$
and $s=1$![]() for $\beta \neq 0$
for $\beta \neq 0$![]() .
.
Since $q_{\beta \neq 0}(1)=q_0(0)=1$![]() , from (A.20) and (A.21), we have
, from (A.20) and (A.21), we have

Now, differentiating $\log f_{\beta }(s)$![]() with respect to $s$
with respect to $s$![]() and using (A.20), we obtain
and using (A.20), we obtain

If $\tau =0$![]() , then from (A.22) and (A.23), we get
, then from (A.22) and (A.23), we get

and if $\tau >0$![]() , from (A.21), we have
, from (A.21), we have

From (A.2) and (A.4), it follows that $\mu \leq \sigma _2$![]() and then
and then

Therefore, concerning the cases $s=0$![]() for $\beta = 0$
for $\beta = 0$![]() and $s=1$
and $s=1$![]() for $\beta \neq 0$
for $\beta \neq 0$![]() , we have
, we have

For the case when $\beta <0$![]() and $\tau \geq 0$
and $\tau \geq 0$![]() , we rewrite $q_{\beta }(s)$
, we rewrite $q_{\beta }(s)$![]() to get
to get

From (A.2) and (A.15), it follows that $k\mu -\tau =2k+\sigma _1-\tau >0$![]() . Then
. Then
Thus, from (A.20), (A.23) and (A.28), for $\beta \neq 0$![]() , we get
, we get

as $s\to 0$![]() .
.
Therefore, from (A.29), we obtain

and

Collecting (A.22), (A.24), (A.27), (A.30) and (A.31), there exists a $C^1$![]() -extension for $f_{\beta }(s)$
-extension for $f_{\beta }(s)$![]() when $s\not \in I_{\beta }$
when $s\not \in I_{\beta }$![]() , and we have that $u_{\beta }$
, and we have that $u_{\beta }$![]() is a radial solution of (1.1) with $g=g_{\beta }$
is a radial solution of (1.1) with $g=g_{\beta }$![]() , where
, where

Step 2. For $\beta$![]() satisfying the inequality (A.5), $u_{\beta }$
satisfying the inequality (A.5), $u_{\beta }$![]() is a semistable solution of (1.1).
is a semistable solution of (1.1).
Next, for suitable $\rho,\,\theta$![]() and $V$
and $V$![]() we verify the hypotheses of lemma A.2. To this end, let $V=r^2\lambda _{2,\beta }^{k+1}$
we verify the hypotheses of lemma A.2. To this end, let $V=r^2\lambda _{2,\beta }^{k+1}$![]() . Differentiating $\log V$
. Differentiating $\log V$![]() with respect to $r$
with respect to $r$![]() , from (A.10), (A.16) and (A.17), we have
, from (A.10), (A.16) and (A.17), we have
Note that in both cases $\tau =0$![]() or $\tau >0$
or $\tau >0$![]() , we have that $n>k(k+1)/(2k+\sigma _1)$
, we have that $n>k(k+1)/(2k+\sigma _1)$![]() and $k+\sigma _1>0$
and $k+\sigma _1>0$![]() by (A.3) and (A.4). Now, since
by (A.3) and (A.4). Now, since
it follows that $n>-(k+1)(\sigma _1/k)$![]() . Combining this with (A.2) and (A.16), we have
. Combining this with (A.2) and (A.16), we have
with $C_{\beta }=\left \vert \beta \right \vert ^{k+1}$![]() for $\beta \neq 0$
for $\beta \neq 0$![]() and $C_{\beta }=1$
and $C_{\beta }=1$![]() for $\beta =0$
for $\beta =0$![]() .
.
Now, consider $\rho =v$![]() and $\theta =2\nu$
and $\theta =2\nu$![]() . From (A.33), we have
. From (A.33), we have
We have from (A.5) that

From this we obtain

Consider the function

Note that $\partial _r(\int _1^r{\frac {v(s)ds}{s}}-v(r)\log r)=-v'(r)\log r\geq 0$![]() for any $r\geq 1$
for any $r\geq 1$![]() by (A.13). Then $\int _1^r{\frac {v(s)ds}{s}}-v(r)\log r\geq 0$
by (A.13). Then $\int _1^r{\frac {v(s)ds}{s}}-v(r)\log r\geq 0$![]() for every $r\geq 1$
for every $r\geq 1$![]() . Therefore $A(r)\geq 0$
. Therefore $A(r)\geq 0$![]() for every $r\geq 0$
for every $r\geq 0$![]() . Now since, $\beta \geq Q(r)$
. Now since, $\beta \geq Q(r)$![]() and $h_{\mu }(r)\in [0,\,1)$
and $h_{\mu }(r)\in [0,\,1)$![]() , it follows that
, it follows that
We claim that
Using (A.2), (A.12) and (A.13), we can easily see that
Let us now consider the functions:
Since $n>k/(v(0)+1)$![]() by (2.10), we have
by (2.10), we have

From this and the fact that $\nu \geq 0$![]() by (A.19), it follows that $I_+>0$
by (A.19), it follows that $I_+>0$![]() .
.
On the other hand, from (A.5), (A.37) and (A.38), we have

It follows that

In the following, we will prove that $I_{-}I_+\geq 0$![]() , which implies that $I_{-}\geq 0$
, which implies that $I_{-}\geq 0$![]() since $I_+>0$
since $I_+>0$![]() . To do that, we begin by noting that
. To do that, we begin by noting that
and
where $B(r):=\frac {(k^2+1)(v(0)+1)}{k}+n-2k+\frac {2\tau }{k+1}h_{\sigma _2}(r)$![]() . Using that
. Using that

together with (A.39) and (A.41) we then have

If $\tau =0$![]() , we are done. So assume that $\tau >0$
, we are done. So assume that $\tau >0$![]() , then
, then

by (A.4). From this and (A.42), $I_{-}I_+\geq 0$![]() , which proves the claim (A.36).
, which proves the claim (A.36).
Thus, according to (A.35) and (A.36), we have
Hence, from the previous inequality and from (A.34), we conclude that the conditions (A.7) and (A.8) of lemma A.2 are satisfied. Recall that $V=r^2\lambda _{2,\beta }^{k+1},\, \rho =v$![]() and $\theta =2\nu$
and $\theta =2\nu$![]() , then one can see from (A.9) and (A.19) that
, then one can see from (A.9) and (A.19) that

for every radially symmetric function $\eta \in C^1_c(\mathbb {R}^n)$![]() .
.
Therefore, from lemma 2.1 and corollary 1.8 of [Reference Navarro and Sánchez7], we have that $u_\beta$![]() is a semi-stable solution of (1.1). Although only the case of a ball appears in corollary 1.8, one can see that the proof of this lemma can be adapted without difficulties to the $\mathbb {R}^n$
is a semi-stable solution of (1.1). Although only the case of a ball appears in corollary 1.8, one can see that the proof of this lemma can be adapted without difficulties to the $\mathbb {R}^n$![]() space.
space.
Proof of remark 1.5. Let $u_{\beta }$![]() as in remark 1.5 a semi-stable solution of (1.1). From theorem 1.4, there exist $M>0$
as in remark 1.5 a semi-stable solution of (1.1). From theorem 1.4, there exist $M>0$![]() and $r_0\geq 1$
and $r_0\geq 1$![]() , such that for any $r\geq r_0$
, such that for any $r\geq r_0$![]() , we have
, we have
• If $n\neq 2(k+\tfrac {2\sigma _1}{k}+4)$
 ,
,
• If $\beta \neq 0$
 , then
(A.43)\begin{equation} C_{\beta}r^{\beta-\delta(r)}\geq\frac{\left\vert u_{\beta}(r)\right\vert}{r^{\delta(r)}}\geq M, \end{equation}where $C_{\beta }=2^{\beta /\mu }$
, then
(A.43)\begin{equation} C_{\beta}r^{\beta-\delta(r)}\geq\frac{\left\vert u_{\beta}(r)\right\vert}{r^{\delta(r)}}\geq M, \end{equation}where $C_{\beta }=2^{\beta /\mu }$
 if $\beta >0$
if $\beta >0$ and $C_{\beta }=1$
and $C_{\beta }=1$ if $\beta <0$
if $\beta <0$ ,
,• If $\beta =0$
 , then
(A.44)\begin{equation} \left(\frac{\log 2}{\mu}+\log r\right) r^{-\delta(r)}\geq\frac{\left\vert u_{0}(r)\right\vert}{r^{\delta(r)}}\geq M, \end{equation}
, then
(A.44)\begin{equation} \left(\frac{\log 2}{\mu}+\log r\right) r^{-\delta(r)}\geq\frac{\left\vert u_{0}(r)\right\vert}{r^{\delta(r)}}\geq M, \end{equation}
• If $n=2(k+\frac {2\sigma _1}{k}+4)$
 and $\beta \neq 0$
and $\beta \neq 0$ , then
(A.45)\begin{equation} C_{\beta}\frac{r^{\beta}}{\log r}\geq\frac{\left\vert u_{\beta}(r)\right\vert}{\log r}\geq M, \end{equation}where $C_{\beta }$
, then
(A.45)\begin{equation} C_{\beta}\frac{r^{\beta}}{\log r}\geq\frac{\left\vert u_{\beta}(r)\right\vert}{\log r}\geq M, \end{equation}where $C_{\beta }$
 is as in (A.43).
is as in (A.43).
Now, let $\tau =0$![]() in (A.1), then $w(r)=r^{\sigma _1}$
in (A.1), then $w(r)=r^{\sigma _1}$![]() . Thus from (1.6) and (A.5) we get
. Thus from (1.6) and (A.5) we get
So, if $\delta _{\infty }(\sigma _1)>\beta$![]() , we have
, we have
• If $n\neq 2(k+\frac {2\sigma _1}{k}+4)$
 , from (A.43) and (A.44), letting $r\to +\infty$
, from (A.43) and (A.44), letting $r\to +\infty$ , we obtain a contradiction.
, we obtain a contradiction.• If $n=2(k+\frac {2\sigma _1}{k}+4)$
 , from (2.22), we have that $\delta _{\infty }(\sigma _1)=0$
, from (2.22), we have that $\delta _{\infty }(\sigma _1)=0$ and from (A.45), letting $r\to +\infty$
and from (A.45), letting $r\to +\infty$ , we obtain a contradiction.
, we obtain a contradiction.
Hence, $\beta \geq \delta _{\infty }(\sigma _1)=\delta (r)=Q(r),\,\forall r\geq 1$![]() .
.
In addition, it is easy to check that for any $r\geq 1$![]() , we have that
, we have that
• If $n\neq 2(k+\frac {2\sigma _1}{k}+4)$
 ,
\[ \frac{\left\vert u_{\beta}(r)\right\vert}{r^{\delta_{\infty}(\sigma_1)}}\geq\begin{cases} 2^{\frac{\beta}{\mu}} & \mbox{if }\beta<0,\\ \frac{1}{\mu}\log 2 & \mbox{if }\beta=0,\\ 1 & \mbox{if }\beta>0. \end{cases} \]
,
\[ \frac{\left\vert u_{\beta}(r)\right\vert}{r^{\delta_{\infty}(\sigma_1)}}\geq\begin{cases} 2^{\frac{\beta}{\mu}} & \mbox{if }\beta<0,\\ \frac{1}{\mu}\log 2 & \mbox{if }\beta=0,\\ 1 & \mbox{if }\beta>0. \end{cases} \]
• If $n=2(k+\frac {2\sigma _1}{k}+4)$
 ,
\[ \frac{\left\vert u_{\beta}(r)\right\vert}{\log r}\geq\begin{cases} \beta e & \mbox{if }\beta>0,\\ 1 & \mbox{if }\beta=0. \end{cases} \]
,
\[ \frac{\left\vert u_{\beta}(r)\right\vert}{\log r}\geq\begin{cases} \beta e & \mbox{if }\beta>0,\\ 1 & \mbox{if }\beta=0. \end{cases} \]
Therefore, we conclude that theorem 1.4 is sharp for $\gamma =\sigma _1>-k$![]() and $w(r)=r^{\sigma _1}$
and $w(r)=r^{\sigma _1}$![]() where
where

and $r_0=1$![]() .
.
Proof of remark 1.7. Let $\beta <0$![]() such that (A.5) holds. From example A.1 $u_{\beta }(r)=-(1+r^\mu )^\frac {\beta }{\mu }$
such that (A.5) holds. From example A.1 $u_{\beta }(r)=-(1+r^\mu )^\frac {\beta }{\mu }$![]() is a semi-stable bounded solution of (1.1). Now note that from (2.12), (A.12), (A.13) and the fact that, for $r\geq 1$
is a semi-stable bounded solution of (1.1). Now note that from (2.12), (A.12), (A.13) and the fact that, for $r\geq 1$![]() , $h_{\sigma _2}(r)\in [1/2,\,1)$
, $h_{\sigma _2}(r)\in [1/2,\,1)$![]() , $h'_{\sigma _2}(r)>0$
, $h'_{\sigma _2}(r)>0$![]() , we have
, we have

From this and (A.19), we obtain

Hence, from (2.23), (A.5) and (A.14), we have

From this, we have that $0>\beta \geq \delta (r) ,\,\forall r\geq 1$![]() and item $i)$
and item $i)$![]() follows from (2.22).
follows from (2.22).
Since $\beta -\delta (r)\geq 0$![]() for any $r\geq 1,\, u_{\beta,\infty }=\lim _{r\to +\infty }{u_{\beta }(r)}=0$
for any $r\geq 1,\, u_{\beta,\infty }=\lim _{r\to +\infty }{u_{\beta }(r)}=0$![]() and $(1+r^{-\mu })^{\frac {\beta }{\mu }}\geq 2^{\frac {\beta }{\mu }}$
and $(1+r^{-\mu })^{\frac {\beta }{\mu }}\geq 2^{\frac {\beta }{\mu }}$![]() , from (A.46), we finally obtain
, from (A.46), we finally obtain
and item $ii)$![]() follows.
follows.