Let $F$ be a unramified finite extension of $\mathbb{Q}_{p}$ and $\overline{\unicode[STIX]{x1D70C}}$ be an irreducible mod $p$ two-dimensional representation of the absolute Galois group of $F$. The aim of this article is the explicit computation of the Kisin variety parameterizing the Breuil–Kisin modules associated to certain families of potentially Barsotti–Tate deformations of $\overline{\unicode[STIX]{x1D70C}}$. We prove that this variety is a finite union of products of $\mathbb{P}^{1}$. Moreover, it appears as an explicit closed connected subvariety of $(\mathbb{P}^{1})^{[F:\mathbb{Q}_{p}]}$. We define a stratification of the Kisin variety by locally closed subschemes and explain how the Kisin variety equipped with its stratification may help in determining the ring of Barsotti–Tate deformations of $\overline{\unicode[STIX]{x1D70C}}$.

Let $p\geqslant 5$ be a prime, and let ${\mathcal{O}}$ be the ring of integers of a finite extension $K$ of $\mathbb{Q}_{p}$ with uniformizer ${\it\pi}$. Let ${\it\rho}_{n}:G_{\mathbb{Q}}\rightarrow \mathit{GL}_{2}\left({\mathcal{O}}/({\it\pi}^{n})\right)$ have modular mod-${\it\pi}$ reduction $\bar{{\it\rho}}$, be ordinary at $p$, and satisfy some mild technical conditions. We show that ${\it\rho}_{n}$ can be lifted to an ${\mathcal{O}}$-valued characteristic-zero geometric representation which arises from a newform. This is new in the case when $K$ is a ramified extension of $\mathbb{Q}_{p}$. We also show that a prescribed ramified complete discrete valuation ring ${\mathcal{O}}$ is the weight-$2$ deformation ring for $\bar{{\it\rho}}$ for a suitable choice of auxiliary level. This implies that the field of Fourier coefficients of newforms of weight 2, square-free level, and trivial nebentype that give rise to semistable $\bar{{\it\rho}}$ of weight 2 can have arbitrarily large ramification index at $p$.

We prove that, for any prime ℓ and any even integer n, there are infinitely many exponents k for which appears as a Galois group over . This generalizes a result of Wiese from 2006, which inspired this paper.

This paper is a continuation of our previous work (D. Jiang and D. Soudry, On the genericity of cuspidal automorphic forms on${\rm SO}_{2n+1}$, J. reine angew. Math., to appear). We extend Moeglin's results (C. Moeglin, J. Lie Theory 7 (1997), 201–229, 231–238) from the even orthogonal groups to old orthogonal groups and complete our proof of the CAP conjecture for irreducible cuspidal automorphic representations of $\mathrm{SO}_{2n+1}(\mathbb{A})$ with special Bessel models. We also give a characterization of the vanishing of the central value of the standard $L$-function of $\mathrm{SO}_{2n+1}(\mathbb{A})$ in terms of theta correspondence. As a result, we obtain the weak Langlands functorial transfer from $\mathrm{SO}_{2n+1}(\mathbb{A})$ to $\mathrm{GL}_{2n}(\mathbb{A})$ for irreducible cuspidal automorphic representations of $\mathrm{SO}_{2n+1}(\mathbb{A})$ with special Bessel models.

In a 1987 paper, Gross introduced certain curves associated to a definite quaternion algebra $B$ over $\mathbf{Q}$; he then proved an analog of his result with Zagier for these curves. In Gross’ paper, the curves were defined in a somewhat ad hoc manner. In this article, we present an interpretation of these curves as projective varieties arising from graded rings of automorphic forms on ${{B}^{\times }}$, analogously to the construction in the Satake compactification. To define such graded rings, one needs to introduce a “multiplication” of automorphic forms that arises from the representation ring of ${{B}^{\times }}$. The resulting curves are unions of projective lines equipped with a collection of Hecke correspondences. They parametrize two-dimensional complex tori with quaternionic multiplication. In general, these complex tori are not abelian varieties; they are algebraic precisely when they correspond to $\text{CM}$ points on these curves, and are thus isogenous to a product $E\,\times \,E$, where $E$ is an elliptic curve with complex multiplication. For these $\text{CM}$ points one can make a relation between the action of the $p$-th Hecke operator and Frobenius at $p$, similar to the well-known congruence relation of Eichler and Shimura.

In this paper we use Langlands-Shahidi method and the result of Langlands which says that non self-conjugate maximal parabolic subgroups do not contribute to the residual spectrum, to prove the holomorphy of several completed automorphic $L$-functions on the whole complex plane which appear in constant terms of the Eisenstein series. 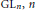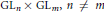They include the exterior square $L$-functions of $\text{G}{{\text{L}}_{\text{n}}},\,n$ odd, the Rankin-Selberg $L$-functions of $\text{G}{{\text{L}}_{n}}\times \,\text{G}{{\text{L}}_{m}},\,n\,\ne \,m$, and $L$-functions 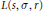$L\left( s,\,\sigma ,\,r \right)$, where $\sigma $ is a generic cuspidal representation of 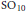$\text{S}{{\text{O}}_{10}}$ and $r$ is the half-spin representation of GSpin 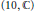$\left( 10,\,\mathbb{C} \right)$. The main part is proving the holomorphy and non-vanishing of the local normalized intertwining operators by reducing them to natural conjectures in harmonic analysis, such as standard module conjecture.

Let G be a complex reductive group, and G^ its set of irreducible admissible representations. The Bruhat order on G^ is defined in a natural way. We prove that this Bruhat order is preserved by transfer. This gives new proofs of some results by the author on L-functions.