Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T21:22:17.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Langlands-Shahidi Method and Poles of Automorphic L-Functions: Application to Exterior Square L-Functions

Published online by Cambridge University Press:  20 November 2018

Henry H. Kim
Henry H. Kim*
Affiliation:
Department of Mathematics, Southern Illinois University, Carbondale, IL 62901, USA email: henrykim@math.siu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we use Langlands-Shahidi method and the result of Langlands which says that non self-conjugate maximal parabolic subgroups do not contribute to the residual spectrum, to prove the holomorphy of several completed automorphic $L$-functions on the whole complex plane which appear in constant terms of the Eisenstein series. 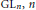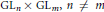They include the exterior square $L$-functions of $\text{G}{{\text{L}}_{\text{n}}},\,n$ odd, the Rankin-Selberg $L$-functions of $\text{G}{{\text{L}}_{n}}\times \,\text{G}{{\text{L}}_{m}},\,n\,\ne \,m$, and $L$-functions 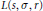$L\left( s,\,\sigma ,\,r \right)$, where $\sigma $ is a generic cuspidal representation of 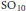$\text{S}{{\text{O}}_{10}}$ and $r$ is the half-spin representation of GSpin 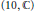$\left( 10,\,\mathbb{C} \right)$. The main part is proving the holomorphy and non-vanishing of the local normalized intertwining operators by reducing them to natural conjectures in harmonic analysis, such as standard module conjecture.

Keywords

11F22E
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 4 , 01 August 1999 , pp. 835 - 849
Copyright
Copyright © Canadian Mathematical Society 1999

References

[Bu-Fr] Bump, D. and Friedberg, S., The exterior square automorphic L-functions on GL(n). Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday, Part II (Ramat Aviv, 1989), Israel Math. Conf. Proc. 3,Weizmann, Jerusalem, 1990, 47–65.Google Scholar
[C-Sh] Casselman, W. and Shahidi, F., On irreducibility of standard modules for generic representations. Ann. Sci. École Norm. Sup. Sér. 4 31(1998), 561–589.Google Scholar
[Ge-Sh] Gelbart, S. and Shahidi, F., Analytic Properties of Automorphic L-Functions. Academic Press, 1988.Google Scholar
[J-S1] Jacquet, H. and Shalika, J., On Euler products and the classification of automorphic forms II. Amer. J. Math. 103(1981), 777–815.Google Scholar
[J-S2] Jacquet, H. and Shalika, J., Exterior square L-functions. In: Automorphic forms, Shimura varieties, and L-functions, Vol. II (Ann Arbor, MI, 1988), Academic Press, 1990, 143–226.Google Scholar
[K1] Kim, H., The residual spectrum of Sp4. Compositio Math. 99(1995), 129–151.Google Scholar
[K2] Kim, H., The residual spectrum of G2. Canad. J. Math. (6) 48(1996), 1245–1272.Google Scholar
[Ki-Sh] Kim, H. and Shahidi, F., Symmetric cube L-functions of GL2 are entire. Ann. of Math., to appear.Google Scholar
[La1] Langlands, R. P., Euler Products. Yale University Press, 1971.Google Scholar
[La2] Langlands, R. P., On the Functional Equations Satisfied by Eisenstein Series. Lecture Notes in Math. 544, Springer-Verlag, 1976.Google Scholar
[M-W1] Moeglin, C. and Waldspurger, J. L., Spectral Decomposition and Eisenstein series, une paraphrase de l’Ecriture. Cambridge Tracts in Math. 113, Cambridge University Press, 1995.Google Scholar
[M-W2] Moeglin, C. and Waldspurger, J. L., Le spectre résiduel de GL(n). Ann. Sci. École Norm. Sup. (4) 22(1989), 605–674.Google Scholar
[Mu1] Muíc, G., The unitary dual of p-adic G2. Duke Math. J. 90(1997), 465–493.Google Scholar
[Mu2] Muíc, G., Some results on square integrable representations; irreducibility of standard representations. Internat.Math. Res. Notices 14(1998), 705–726.Google Scholar
[Mu-Sh] Muíc, G. and Shahidi, F., Irreducibility of standard representations for Iwahori-spherical representations. Preprint, 1997.Google Scholar
[Sh1] Shahidi, F., A proof of Langlands conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. 132(1990), 273–330.Google Scholar
[Sh2] Shahidi, F., On multiplicativity of local factors. In: Festschrift in honor of I. I. Piatetski–Shapiro, Part II, Israel Math. Conf. Proc. 3, Weizmann, Jerusalem, 1990, 279–289.Google Scholar
[Sh3] Shahidi, F., On certain L-functions. Amer. J. Math. 103(1981), 297–355.Google Scholar
[Sh4] Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions. Ann. of Math. 127(1988), 547–584.Google Scholar
[Sh5] Shahidi, F., Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke Math. J. (1) 66(1992), 1–41.Google Scholar
[Sh6] Shahidi, F., Automorphic L-functions: a survey. In: Automorphic forms, Shimura varieties, and Lfunctions, Vol. II (Ann Arbor, MI, 1988), Academic Press, 1990, 415–437.Google Scholar
[Ta] Tadic, M., Classification of unitary representations in irreducible representations of general linear group (non-Archimedean case). Ann. Sci. École Norm. Sup. (4) 19(1986), 335–382.Google Scholar
[Vo] Vogan, D., The unitary dual of GL(n)over an archimedean field. Invent.Math. 83(1986), 449–505.Google Scholar
[Zh] Zhang, Y., The holomorphy and nonvanishing of normalized local intertwining operators. Pacific. J. Math. 180(1997), 358–398.Google Scholar