Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-07T03:57:55.685Z Has data issue: false hasContentIssue false
  • English
  • Français

LIFTING TORSION GALOIS REPRESENTATIONS

Published online by Cambridge University Press:  24 August 2015

CHANDRASHEKHAR KHARE  and
RAVI RAMAKRISHNA
CHANDRASHEKHAR KHARE
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA; shekhar@math.ucla.edu
RAVI RAMAKRISHNA
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853-4210, USA; ravi@math.cornell.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 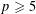$p\geqslant 5$ be a prime, and let 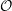${\mathcal{O}}$ be the ring of integers of a finite extension 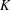$K$ of 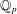$\mathbb{Q}_{p}$ with uniformizer ${\it\pi}$. Let 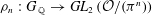${\it\rho}_{n}:G_{\mathbb{Q}}\rightarrow \mathit{GL}_{2}\left({\mathcal{O}}/({\it\pi}^{n})\right)$ have modular mod-${\it\pi}$ reduction $\bar{{\it\rho}}$, be ordinary at 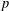$p$, and satisfy some mild technical conditions. We show that 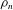${\it\rho}_{n}$ can be lifted to an 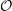${\mathcal{O}}$-valued characteristic-zero geometric representation which arises from a newform. This is new in the case when 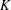$K$ is a ramified extension of 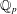$\mathbb{Q}_{p}$. We also show that a prescribed ramified complete discrete valuation ring 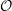${\mathcal{O}}$ is the weight-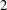$2$ deformation ring for 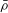$\bar{{\it\rho}}$ for a suitable choice of auxiliary level. This implies that the field of Fourier coefficients of newforms of weight 2, square-free level, and trivial nebentype that give rise to semistable 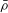$\bar{{\it\rho}}$ of weight 2 can have arbitrarily large ramification index at 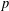$p$.

Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e14
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Atiyah, M. and MacDonald, I., Introduction to Commutative Algebra (Addison-Wesley, Reading, MA, 1969).Google Scholar
Boston, N., ‘Appendix to On p-adic analytic families of Galois representations by B. Mazur and A. Wiles’, Compos. Math. 59 (1986), 231–264.Google Scholar
Camporino, M. and Pacetti, A., ‘Congruences between modular forms modulo prime powers’, Preprint.Google Scholar
Darmon, H., Diamond, F. and Taylor, R., Fermat’s Last Theorem, Current Developments in Mathematics, 1 (International Press, 1995), 1–157. Reprinted in Elliptic curves, modular forms & Fermat’s last theorem (Hong Kong, 1993), 2–140, International Press, Cambridge, MA, 1997.Google Scholar
Diamond, F. and Taylor, R., ‘Nonoptimal levels of mod l modular representations’, Invent. Math. 115(3) (1994), 435–462.Google Scholar
Flach, M., ‘A finiteness theorem for the symmetric square of an elliptic curve’, Invent. Math. 109 (1992), 307–327.CrossRefGoogle Scholar
Fontaine, J.-M. and Lafaille, G., ‘Construction de représentaions p-adiques’, Ann. Sci. Éc. Norm. Supér. (4) 15 (1982), 179–207.Google Scholar
Hamblen, S. and Ramakrishna, R., ‘Deformations of certain reducible Galois representations, II’, Amer. J. Math. 130 913–944.CrossRefGoogle Scholar
Khare, C., ‘Modularity of p-adic Galois representations via p-adic approximations’, J. Théor. Nombres Bordeaux 16 (2004), 179–185.Google Scholar
Khare, C., Larsen, M. and Ramakrishna, R., ‘Constructing semisimple p-adic Galois representations with prescribed properties’, Amer. J. Math. 127(4) (2005), 709–734.Google Scholar
Lundell, B., ‘Selmer groups and ranks of Hecke rings’, PhD Thesis, Cornell University, 2011.Google Scholar
Ramakrishna, R., ‘Lifting Galois representations’, Invent. Math. 138(3) (1999), 537–562.Google Scholar
Ramakrishna, R., ‘Deforming Galois representations and the conjectures of Serre and Fontaine-Mazur’, Ann. of Math. (2) 156(1) (2002), 115–154.Google Scholar
Ramakrishna, R., ‘Constructing Galois representations with very large image’, Canad. J. Math. 60(1) (2008), 208–221.Google Scholar
Ramakrishna, R., ‘Maps to weight space in Hida families’, Indian J. Pure Appl. Math. 45(5) (2014), 759–776.Google Scholar
Ribet, K., ‘Report on mod ℓ representations of Gal(ℚ∕ℚ)’, Motives II PSPM 55.2 (1991), 639–676.Google Scholar
Taylor, R., ‘On icosahedral Artin representations. II’, Amer. J. Math. 125(3) (2003), 549–566.Google Scholar
Thorne, J., ‘Automorphy of some residually dihedral Galois representations’, Preprint.Google Scholar
Wiles, A., ‘Modular elliptic curves and Fermat’s last theorem’, Ann. of Math. (2) 141(3) (1995), 443–551.Google Scholar