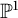 $\mathbb {P}^1$
$\mathbb {P}^1$
 $\mathscr{D}$-modules and index theorems
$\mathscr{D}$-modules and index theorems
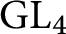 $ \operatorname {{\mathrm {GL}}}_4$
$ \operatorname {{\mathrm {GL}}}_4$