We study a quiver description of the nested Hilbert scheme of points on the affine plane and its higher rank generalization – that is, the moduli space of flags of framed torsion-free sheaves on the projective plane. We show that stable representations of the quiver provide an ADHM-like construction for such moduli spaces. We introduce a natural torus action and use equivariant localization to compute some of their (virtual) topological invariants, including the case of compact toric surfaces. We conjecture that the generating function of holomorphic Euler characteristics for rank one is given in terms of polynomials in the equivariant weights, which, for specific numerical types, coincide with (modified) Macdonald polynomials. From the physics viewpoint, the quivers we study describe a class of surface defects in four-dimensional supersymmetric gauge theories in terms of nested instantons.

We study the spaces of twisted conformal blocks attached to a $\Gamma$-curve $\Sigma$ with marked $\Gamma$-orbits and an action of $\Gamma$ on a simple Lie algebra $\mathfrak {g}$, where $\Gamma$ is a finite group. We prove that if $\Gamma$ stabilizes a Borel subalgebra of $\mathfrak {g}$, then the propagation theorem and factorization theorem hold. We endow a flat projective connection on the sheaf of twisted conformal blocks attached to a smooth family of pointed $\Gamma$-curves; in particular, it is locally free. We also prove that the sheaf of twisted conformal blocks on the stable compactification of Hurwitz stack is locally free. Let $\mathscr {G}$ be the parahoric Bruhat–Tits group scheme on the quotient curve $\Sigma /\Gamma$ obtained via the $\Gamma$-invariance of Weil restriction associated to $\Sigma$ and the simply connected simple algebraic group $G$ with Lie algebra $\mathfrak {g}$. We prove that the space of twisted conformal blocks can be identified with the space of generalized theta functions on the moduli stack of quasi-parabolic $\mathscr {G}$-torsors on $\Sigma /\Gamma$ when the level $c$ is divisible by $|\Gamma |$ (establishing a conjecture due to Pappas and Rapoport).

Using new explicit formulas for the stationary Gromov–Witten/Pandharipande–Thomas ( $\mathrm {GW}/{\mathrm {PT}}$ ) descendent correspondence for nonsingular projective toric threefolds, we show that the correspondence intertwines the Virasoro constraints in Gromov–Witten theory for stable maps with the Virasoro constraints for stable pairs proposed in [18]. Since the Virasoro constraints in Gromov–Witten theory are known to hold in the toric case, we establish the stationary Virasoro constraints for the theory of stable pairs on toric threefolds. As a consequence, new Virasoro constraints for tautological integrals over Hilbert schemes of points on surfaces are also obtained.

We construct natural operators connecting the cohomology of the moduli spaces of stable Higgs bundles with different ranks and genera which, after numerical specialisation, recover the topological mirror symmetry conjecture of Hausel and Thaddeus concerning $\mathrm {SL}_n$- and $\mathrm {PGL}_n$-Higgs bundles. This provides a complete description of the cohomology of the moduli space of stable $\mathrm {SL}_n$-Higgs bundles in terms of the tautological classes, and gives a new proof of the Hausel–Thaddeus conjecture, which was also proven recently by Gröchenig, Wyss and Ziegler via p-adic integration.

Our method is to relate the decomposition theorem for the Hitchin fibration, using vanishing cycle functors, to the decomposition theorem for the twisted Hitchin fibration, whose supports are simpler.

We conjecture a Verlinde type formula for the moduli space of Higgs sheaves on a surface with a holomorphic 2-form. The conjecture specializes to a Verlinde formula for the moduli space of sheaves. Our formula interpolates between K-theoretic Donaldson invariants studied by Göttsche and Nakajima-Yoshioka and K-theoretic Vafa-Witten invariants introduced by Thomas and also studied by Göttsche and Kool. We verify our conjectures in many examples (for example, on K3 surfaces).

For complex connected, reductive, affine, algebraic groups G, we give a Lie-theoretic characterization of the semistability of principal G-co-Higgs bundles on the complex projective line ℙ1 in terms of the simple roots of a Borel subgroup of G. We describe a stratification of the moduli space in terms of the Harder–Narasimhan type of the underlying bundle.

Let $X$ be a smooth projective curve of arbitrary genus $g\,>\,3$ over the complex numbers. In this short note we will show that the moduli space of rank $2$ stable vector bundles with determinant isomorphic to ${{L}_{x}}$ , where ${{L}_{x}}$ denotes the line bundle corresponding to a point $x\,\in \,X$, is isomorphic to a certain variety of lines in the moduli space of $S$-equivalence classes of semistable bundles of rank $2$ with trivial determinant.

We present a construction of framed torsion free instanton sheaves on a projective variety containing a fixed line which further generalises the one on projective spaces. This is done by generalising the so called ADHM variety. We show that the moduli space of such objects is a quasi projective variety, which is fine in the case of projective spaces. We also give an ADHM categorical description of perverse instanton sheaves in the general case, along with a hypercohomological characterisation of these sheaves in the particular case of projective spaces.

A Hopf surface is the quotient of the complex surface 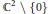${{\mathbb{C}}^{2}}\,\backslash \,\left\{ 0 \right\}$ by an infinite cyclic group of dilations of 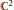${{\mathbb{C}}^{2}}$. In this paper, we study the moduli spaces 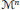${{\mathcal{M}}^{n}}$ of stable 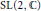$\text{SL}\left( 2,\,\mathbb{C} \right)$-bundles on a Hopf surface 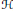$\mathcal{H}$, from the point of view of symplectic geometry. An important point is that the surface 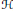$\mathcal{H}$ is an elliptic fibration, which implies that a vector bundle on 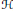$\mathcal{H}$ can be considered as a family of vector bundles over an elliptic curve. We define a map 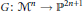$G:\,{{\mathcal{M}}^{n}}\,\to \,{{\mathbb{P}}^{2n+1}}$ that associates to every bundle on 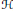$\mathcal{H}$ a divisor, called the graph of the bundle, which encodes the isomorphism class of the bundle over each elliptic curve. We then prove that the map 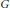$G$ is an algebraically completely integrable Hamiltonian system, with respect to a given Poisson structure on 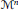${{\mathcal{M}}^{n}}$. We also give an explicit description of the fibres of the integrable system. This example is interesting for several reasons; in particular, since the Hopf surface is not Kähler, it is an elliptic fibration that does not admit a section.