Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T13:47:09.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrable Systems Associated to a Hopf Surface

Published online by Cambridge University Press:  20 November 2018

Ruxandra Moraru
Ruxandra Moraru*
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, Quebec H3A 2K6 e-mail: moraru@math.mcgill.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A Hopf surface is the quotient of the complex surface 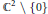${{\mathbb{C}}^{2}}\,\backslash \,\left\{ 0 \right\}$ by an infinite cyclic group of dilations of 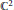${{\mathbb{C}}^{2}}$. In this paper, we study the moduli spaces 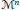${{\mathcal{M}}^{n}}$ of stable 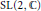$\text{SL}\left( 2,\,\mathbb{C} \right)$-bundles on a Hopf surface 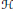$\mathcal{H}$, from the point of view of symplectic geometry. An important point is that the surface 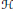$\mathcal{H}$ is an elliptic fibration, which implies that a vector bundle on 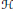$\mathcal{H}$ can be considered as a family of vector bundles over an elliptic curve. We define a map 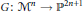$G:\,{{\mathcal{M}}^{n}}\,\to \,{{\mathbb{P}}^{2n+1}}$ that associates to every bundle on 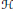$\mathcal{H}$ a divisor, called the graph of the bundle, which encodes the isomorphism class of the bundle over each elliptic curve. We then prove that the map 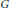$G$ is an algebraically completely integrable Hamiltonian system, with respect to a given Poisson structure on 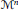${{\mathcal{M}}^{n}}$. We also give an explicit description of the fibres of the integrable system. This example is interesting for several reasons; in particular, since the Hopf surface is not Kähler, it is an elliptic fibration that does not admit a section.

Keywords

14J6014D2114H7014J27
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 55 , Issue 3 , 01 June 2003 , pp. 609 - 635
Copyright
Copyright © Canadian Mathematical Society 2003

References

[At] Atiyah, M. F. Vector bundles over an elliptic curve. Proc. LondonMath. Soc. (3) 7(1957), 414–452.Google Scholar
[Ba] Barth, W. Some properties of stable rank-2 vector bundles on Pn. Math. Ann. 226(1977), 125–150.Google Scholar
[Be] Beauville, A. Systèmes hamiltoniens complètement intégrables associés aux surfaces K3. Sympos. Math. 32(1992), 25–31.Google Scholar
[BH] Braam, P. J. and Hurtubise, J. Instantons on Hopf surfaces and monopoles on solid tori. J. Reine Angew.Math. 400(1989), 146–172.Google Scholar
[BHMM] Boyer, C., Hurtubise, J., Mann, B. M. and Milgram, R. J. The topology of instanton moduli spaces, I: The Atiyah-Jones conjecture. Ann. of Math. (2) 137(1993), 561–609.Google Scholar
[Bo1] Bottacin, F. Poisson structures on moduli spaces of sheaves over Poisson surfaces. Invent.Math. 121(1995), 421–436.Google Scholar
[Bo2] Bottacin, F. Symplectic geometry on moduli spaces of stable pairs. Ann. Sci. École Norm. Sup. (4) 28(1995), 391–433.Google Scholar
[Bh] Buchdahl, N. P. Hermitian-Einstein connections and stable vector bundles over compact complex surfaces. Math. Ann. 280(1978), 625–648.Google Scholar
[F] Friedman, R., Algebraic Surfaces and Holomorphic Vector Bundles. Universitext, Springer, New York Berlin Heidelberg, 1998.Google Scholar
[FMW] Friedman, R., Morgan, J. and Witten, E. Vector bundles over elliptic fibrations. J. Algebraic Geom. 2(1999), 279–401.Google Scholar
[G] Gauduchon, P. Le théorème de l'excentricité nulle. C. R. Acad. Sci. Paris 285(1977), 387–390.Google Scholar
[H] Hurtubise, J. Instantons and jumping lines. Comm. Math. Phys. 105(1986), 107–122.Google Scholar
[Ha] Hartshorne, R., Algebraic Geometry. Graduate Texts in Math. 52, Springer-Verlag, Berlin-Heidelberg-New York, 1977.Google Scholar
[Hi] Hitchin, N. Stable bundles and integrable systems. Duke Math. J. 54(1987), 91–114.Google Scholar
[Ma] Maruyama, M., Elementary transformations in the theory of algebraic vector bundles. In: Algebraic Geometry (La Rábida, 1981), Lecture Notes in Math. 961, Springer-Verlag, 1982, 241–266.Google Scholar
[Mar] Markman, E. Spectral curves and integrable systems. Compositio Math. 93(1994), 255–290.Google Scholar
[Mo] Moraru, R., Moduli spaces of vector bundles over a Hopf surface, and their stability properties. PhD thesis, McGill University, 2000.Google Scholar
[Mu] Mukai, S. Symplectic structure of the moduli space of sheaves on an abelian or K3 surface. Invent.Math. 77(1984), 101–116.Google Scholar
[T] Teleman, A. Moduli spaces of stable bundles on non-Kählerian elliptic fibre bundles over curves. Expo. Math. 16(1998), 193–248.Google Scholar
[We] Weinstein, A. The local structure of Poisson manifolds. J. Differential Geom. 18(1983), 523–557.Google Scholar