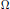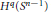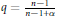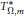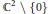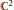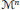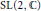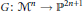Research Article
Graph Subspaces and the Spectral Shift Function
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-503
-
- Article
-
- You have access
- Export citation
Certain Operators with Rough Singular Kernels
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 504-532
-
- Article
-
- You have access
- Export citation
Automorphismes modérés de l'espace affine
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 533-560
-
- Article
-
- You have access
- Export citation
Quasi-Homogeneous Linear Systems on ℙ2 with Base Points of Multiplicity 5
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-575
-
- Article
-
- You have access
- Export citation
Automorphic Orthogonal and Extremal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 576-608
-
- Article
-
- You have access
- Export citation
Integrable Systems Associated to a Hopf Surface
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 609-635
-
- Article
-
- You have access
- Export citation
Higher Dimensional Asymptotic Cycles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 636-648
-
- Article
-
- You have access
- Export citation
Surfaces with pg = q = 2 and an Irrational Pencil
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 649-672
-
- Article
-
- You have access
- Export citation