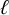 $\ell $
-adic images of Galois for elliptic curves over
$\ell $
-adic images of Galois for elliptic curves over
 $\mathbb {Q}$
(and an appendix with John Voight)
$\mathbb {Q}$
(and an appendix with John Voight)
 $4$
$4$