Let 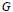$\mathbf {G}$ be a connected reductive algebraic group over an algebraically closed field $\Bbbk $ and ${\mathbf B}$ be a Borel subgroup of ${\mathbf G}$. In this paper, we completely determine the composition factors of the permutation module $\mathbb {F}[{\mathbf G}/{\mathbf B}]$ for any field $\mathbb {F}$.

The Hanna Neumann conjecture is a statement about the rank of the intersection of two finitely generated subgroups of a free group. The conjecture was posed by Hanna Neumann in 1957. In 2011, a strengthened version of the conjecture was proved independently by Joel Friedman and by Igor Mineyev. In this paper we show that the strengthened Hanna Neumann conjecture holds not only in free groups but also in non-solvable surface groups. In addition, we show that a retract in a free group and in a surface group is inert. This implies the Dicks–Ventura inertia conjecture for free and surface groups.

Let p ≥ 3 be a prime. A generalized multi-edge spinal group

$$G = \langle \{ a\} \cup \{ b_i^{(j)} {\rm \mid }1 \le j \le p,\, 1 \le i \le r_j\} \rangle \le {\rm Aut}(T)$$

$b^{(j)}_{1}, \ldots, b^{(j)}_{r_{j}}$

Harish-Chandra induction and restriction functors play a key role in the representation theory of reductive groups over finite fields. In this paper, extending earlier work of Dat, we introduce and study generalisations of these functors which apply to a wide range of finite and profinite groups, typical examples being compact open subgroups of reductive groups over non-archimedean local fields. We prove that these generalisations are compatible with two of the tools commonly used to study the (smooth, complex) representations of such groups, namely Clifford theory and the orbit method. As a test case, we examine in detail the induction and restriction of representations from and to the Siegel Levi subgroup of the symplectic group $\text{Sp}_{4}$ over a finite local principal ideal ring of length two. We obtain in this case a Mackey-type formula for the composition of these induction and restriction functors which is a perfect analogue of the well-known formula for the composition of Harish-Chandra functors. In a different direction, we study representations of the Iwahori subgroup $I_{n}$ of $\text{GL}_{n}(F)$, where $F$ is a non-archimedean local field. We establish a bijection between the set of irreducible representations of $I_{n}$ and tuples of primitive irreducible representations of smaller Iwahori subgroups, where primitivity is defined by the vanishing of suitable restriction functors.

Let $F$ be a field of characteristic $p\geq 0$ and $G$ any group. In this article, the Engel property of the group of units of the group algebra $FG$ is investigated. We show that if $G$ is locally finite, then ${\mathcal{U}}(FG)$ is an Engel group if and only if $G$ is locally nilpotent and $G^{\prime }$ is a $p$-group. Suppose that the set of nilpotent elements of $FG$ is finite. It is also shown that if $G$ is torsion, then ${\mathcal{U}}(FG)$ is an Engel group if and only if $G^{\prime }$ is a finite $p$-group and $FG$ is Lie Engel, if and only if ${\mathcal{U}}(FG)$ is locally nilpotent. If $G$ is nontorsion but $FG$ is semiprime, we show that the Engel property of ${\mathcal{U}}(FG)$ implies that the set of torsion elements of $G$ forms an abelian normal subgroup of $G$.

Nontrivial pairs of zero-divisors in group rings are introduced and discussed. A problem on the existence of nontrivial pairs of zero-divisors in group rings of free Burnside groups of odd exponent $n\,\gg \,1$ is solved in the affirmative. Nontrivial pairs of zero-divisors are also found in group rings of free products of groups with torsion.

Let $R$ be a commutative ring with unity and let $G$ be a group. The group ring $RG$ has a natural involution that maps each element $g\in G$ to its inverse. We denote by $RG^-$ the set of skew symmetric elements under this involution. We study necessary and sufficient conditions for $RG^-$ to be commutative.

Let $G$ be a group, $F$ a field of prime characteristic $p$ and $V$ a finite-dimensional $FG$-module. Let $L(V)$ denote the free Lie algebra on $V$ regarded as an $FG$-submodule of the free associative algebra (or tensor algebra) $T(V)$. For each positive integer $r$, let $L^r (V)$ and $T^r (V)$ be the $r$th homogeneous components of $L(V)$ and $T(V)$, respectively. Here $L^r (V)$ is called the $r$th Lie power of $V$. Our main result is that there are submodules $B_1$, $B_2$, ... of $L(V)$ such that, for all $r$, $B_r$ is a direct summand of $T^r(V)$ and, whenever $m \geqslant 0$ and $k$ is not divisible by $p$, the module $L^{p^mk} (V)$ is the direct sum of $L^{p^m} (B_k)$, $L^{p^{m - 1}} (B_{pk})$, ..., $L^1 (B_{p^mk})$. Thus every Lie power is a direct sum of Lie powers of $p$-power degree. The approach builds on an analysis of $T^r (V)$ as a bimodule for $G$ and the Solomon descent algebra.

A complete structural characterization of submonoids $S$ of a polycyclic-by-finite group such that the semigroup algebra $K[S]$ over a field $K$ is right noetherian is obtained. It follows that such algebras are also left noetherian.

The normalized positive definite class functions $\C G\,{\longrightarrow}\,\C$ are determined for all those direct limits $G$ of finite alternating groups $\Alt(\Omega_i)$ for which the embeddings $\Alt(\Omega_i)\,{\longrightarrow}\,\Alt(\Omega_j)$ are natural in the sense that every non-trivial $\Alt(\Omega_i)$-orbit in $\Omega_j$ is natural.

In this note a proof is given that in the case of finitely generated amenable groups, the classical zero divisor conjecture implies the analytic zero divisor conjecture of Linnell.

Let $G$ be a free product of cyclic groups of prime order. The structure of the unit group $U(\mathbb{Q}G)$ of the rational group ring $\mathbb{Q}G$ is given in terms of free products and amalgamated free products of groups. As an application, all finite subgroups of $U(\mathbb{Q}G)$, up to conjugacy, are described and the Zassenhaus Conjecture for finite subgroups in $\mathbb{Z}G$ is proved. A strong version of the Tits Alternative for $U(\mathbb{Q}G)$ is obtained as a corollary of the structural result.

Let $G$ be any group, and 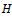$H$ be a normal subgroup of 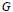$G$. Then M. Hartl identified the subgroup 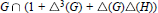$G\,\cap \,(1+\,{{\Delta }^{3}}\,(G)\,+\,\Delta (G)\Delta (H))$ of 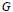$G$. In this note we give an independent proof of the result of Hartl, and we identify two subgroups 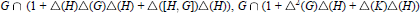$G\,\cap \,(1\,+\,\Delta (H)\Delta (G)\Delta (H)\,+\,\Delta (\left[ H,\,G \right]\Delta (H)),\,G\,\cap \,(1\,+\,{{\Delta }^{2}}\,(G)\Delta (H)\,+\,\Delta (K)\Delta (H))$ of 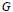$G$ for some subgroup 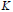$K$ of 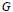$G$ containing 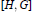$[H,G]$.

We prove the existence of trace functions in the rings of fractions of polycyclic-by-finite group rings or their homomorphic images. In particular a trace function exists in the ring of fractions of KH, where H is a polycyclic-by-finite group and char K > N, where N is a constant depending on H.

Special cases of Bovdi's conjecture are proved. In particular the conjecture is proved for supersolvable and Frobenius groups. We also prove that if is finite, α ∊ VℤG a torsion unit and m the smallest positive integer such that αm ∊ G then m divides .

We give a complete description of the second Fox subgroup G ∩ (1 + Δ2(G)Δ(H)) relative to a given normal subgroup H of an arbitrary finitely generated group G.

Let U(KλG) be the group of units of the infinite twisted group algebra KλG over a field K. We describe the FC-centre ΔU of U(KλG) and give a characterization of the groups G and fields K for which U(KλG) = ΔU. In the case of group algebras we obtain the Cliff-Sehgal-Zassenhaus theorem.

Let KG be the group ring of a group G over a field K and let U(KG) be its group of units. If K has characteristic p > 0 and G contains p-elements, then it is proved that U(KG) is hypercentral if and only if G is nilpotent and G′ is a finite p-group.

In [5], Roggenkamp and Scott gave an affirmative answer to the isomorphism problem for integral group rings of finite p-groups G and H, i.e. to the question whether ZG ⥲ ZH implies G ⥲ H (in this case, G is said to be characterized by its integral group ring). Progress on the analogous question with Z replaced by the field Fp of p elements has been very little during the last couple of years; and the most far reaching result in this area in a certain sense - due to Passi and Sehgal, see [8] - may be compared to the integral case, where the group G is of nilpotency class 2.