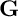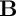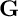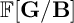1 Introduction
Let
![]() $\mathbf G$
be a connected reductive algebraic group over an algebraically closed field
$\mathbf G$
be a connected reductive algebraic group over an algebraically closed field
![]() $\Bbbk $
and
$\Bbbk $
and
![]() ${\mathbf B}$
be an Borel subgroup of
${\mathbf B}$
be an Borel subgroup of
![]() ${\mathbf G}$
. We will identify
${\mathbf G}$
. We will identify
![]() ${\mathbf G}$
with
${\mathbf G}$
with
![]() ${\mathbf G}(\Bbbk )$
and
${\mathbf G}(\Bbbk )$
and
![]() ${\mathbf B}$
with
${\mathbf B}$
with
![]() ${\mathbf B}(\Bbbk )$
. Let
${\mathbf B}(\Bbbk )$
. Let
![]() $\mathbb {F}$
be another field and all the representations are over
$\mathbb {F}$
be another field and all the representations are over
![]() $\mathbb {F}$
. Now we just regard
$\mathbb {F}$
. Now we just regard
![]() ${\mathbf G}/{\mathbf B}$
as a quotient set and consider the vector space
${\mathbf G}/{\mathbf B}$
as a quotient set and consider the vector space
![]() $\mathbb {F} [{\mathbf G}/{\mathbf B}]$
, which has a basis of the left cosets of
$\mathbb {F} [{\mathbf G}/{\mathbf B}]$
, which has a basis of the left cosets of
![]() ${\mathbf B}$
in
${\mathbf B}$
in
![]() ${\mathbf G}$
. With left multiplication of the group
${\mathbf G}$
. With left multiplication of the group
![]() ${\mathbf G}$
,
${\mathbf G}$
,
![]() $\mathbb {F} [{\mathbf G}/{\mathbf B}]$
is an
$\mathbb {F} [{\mathbf G}/{\mathbf B}]$
is an
![]() $\mathbb {F}{\mathbf G}$
-module, which is isomorphic to
$\mathbb {F}{\mathbf G}$
-module, which is isomorphic to
![]() $\mathbb {F} {\mathbf G} \otimes _{\mathbb {F} \mathbf B} \text {tr}$
, where
$\mathbb {F} {\mathbf G} \otimes _{\mathbb {F} \mathbf B} \text {tr}$
, where
![]() $\text {tr}$
denotes the one-dimensional trivial
$\text {tr}$
denotes the one-dimensional trivial
![]() ${\mathbf B}$
-module. The permutation module
${\mathbf B}$
-module. The permutation module
![]() $\mathbb {F} [{\mathbf G}/{\mathbf B}]$
was studied in [Reference Chen and Dong2] and [Reference Chen and Dong3] when
$\mathbb {F} [{\mathbf G}/{\mathbf B}]$
was studied in [Reference Chen and Dong2] and [Reference Chen and Dong3] when
![]() $\Bbbk = \bar {\mathbb {F}}_q$
, where
$\Bbbk = \bar {\mathbb {F}}_q$
, where
![]() $\bar {\mathbb {F}}_q$
is the algebraically closure of finite field
$\bar {\mathbb {F}}_q$
is the algebraically closure of finite field
![]() $\mathbb {F}_q$
of q elements. In their determination of the composition factors of
$\mathbb {F}_q$
of q elements. In their determination of the composition factors of
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
, the proofs make essential use of the fact that
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
, the proofs make essential use of the fact that
![]() $\bar {\mathbb {F}}_q$
is a union of finite fields.
$\bar {\mathbb {F}}_q$
is a union of finite fields.
The Steinberg module
![]() $\text {St}$
is the socle of
$\text {St}$
is the socle of
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
, and the irreducibility of
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
, and the irreducibility of
![]() $\text {St}$
has been proved by Xi (see [Reference Xi8]) in the case
$\text {St}$
has been proved by Xi (see [Reference Xi8]) in the case
![]() $\Bbbk = \bar {\mathbb {F}}_q$
, and
$\Bbbk = \bar {\mathbb {F}}_q$
, and
![]() $\text {char} \ \mathbb {F} =0 \ \text {or}\ \text {char} \ \bar {\mathbb {F}}_q$
. Later, Yang removed this restriction on
$\text {char} \ \mathbb {F} =0 \ \text {or}\ \text {char} \ \bar {\mathbb {F}}_q$
. Later, Yang removed this restriction on
![]() $\text {char} \ \mathbb {F}$
and proved the irreducibility of Steinberg module for any field
$\text {char} \ \mathbb {F}$
and proved the irreducibility of Steinberg module for any field
![]() $\mathbb {F}$
in [Reference Yang9] (also in the case
$\mathbb {F}$
in [Reference Yang9] (also in the case
![]() $\Bbbk = \bar {\mathbb {F}}_q$
). Recently, Putman and Snowden showed that when
$\Bbbk = \bar {\mathbb {F}}_q$
). Recently, Putman and Snowden showed that when
![]() $\Bbbk $
is an infinite field (not necessary to be algebraically closed), then the Steinberg representation of
$\Bbbk $
is an infinite field (not necessary to be algebraically closed), then the Steinberg representation of
![]() ${\mathbf G}$
is always irreducible for any field
${\mathbf G}$
is always irreducible for any field
![]() $ \mathbb {F}$
(see [Reference Putman and Snowden6]). Their work inspires the idea of the determination of the composition factors of
$ \mathbb {F}$
(see [Reference Putman and Snowden6]). Their work inspires the idea of the determination of the composition factors of
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
for general case in this paper. We will construct a filtration of submodules for
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
for general case in this paper. We will construct a filtration of submodules for
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
whose subquotients are denoted by
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
whose subquotients are denoted by
![]() $E_J$
(indexed by the subsets of the set I of simple reflections). The main theorem is as follows:
$E_J$
(indexed by the subsets of the set I of simple reflections). The main theorem is as follows:
Theorem 1.1. Let
![]() $\mathbb {F}$
be any field. All
$\mathbb {F}$
be any field. All
![]() $\mathbb {F} {\mathbf G}$
-modules
$\mathbb {F} {\mathbf G}$
-modules
![]() $E_J$
are irreducible and pairwise nonisomorphic. Moreover, the
$E_J$
are irreducible and pairwise nonisomorphic. Moreover, the
![]() $\mathbb {F} {\mathbf G}$
-module
$\mathbb {F} {\mathbf G}$
-module
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
has exactly
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
has exactly
![]() $2^{|I|}$
composition factors, each occurring with multiplicity one.
$2^{|I|}$
composition factors, each occurring with multiplicity one.
It is well known that the flag variety
![]() ${\mathbf G}/{\mathbf B}$
plays a very important role in the representation theory. So the decomposition of
${\mathbf G}/{\mathbf B}$
plays a very important role in the representation theory. So the decomposition of
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
may have many applications in other areas such as algebraic geometry and number theory.
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
may have many applications in other areas such as algebraic geometry and number theory.
This paper is organized as follows: Section 2 contains some notations and preliminary results. In particular, we study the properties of the subquotient modules
![]() $E_J$
of
$E_J$
of
![]() $\mathbb {F} [{\mathbf G}/{\mathbf B}]$
. In Section 3, we list some properties of the unipotent radical
$\mathbb {F} [{\mathbf G}/{\mathbf B}]$
. In Section 3, we list some properties of the unipotent radical
![]() ${\mathbf U}$
of
${\mathbf U}$
of
![]() ${\mathbf B}$
and study the self-enclosed subgroup of
${\mathbf B}$
and study the self-enclosed subgroup of
![]() ${\mathbf U}$
, which is useful in the later discussion. Section 4 gives the nonvanishing property of the augmentation. In the last section, we will prove that all the
${\mathbf U}$
, which is useful in the later discussion. Section 4 gives the nonvanishing property of the augmentation. In the last section, we will prove that all the
![]() $\mathbb {F} {\mathbf G}$
-modules
$\mathbb {F} {\mathbf G}$
-modules
![]() $E_J$
are irreducible for any fields
$E_J$
are irreducible for any fields
![]() $\Bbbk $
and
$\Bbbk $
and
![]() $\mathbb {F}$
.
$\mathbb {F}$
.
2 Preliminaries
As in the introduction,
![]() $\mathbf G$
is a connected reductive algebraic group over an algebraically closed field
$\mathbf G$
is a connected reductive algebraic group over an algebraically closed field
![]() $\Bbbk $
and
$\Bbbk $
and
![]() ${\mathbf B}$
is a Borel subgroup. Let
${\mathbf B}$
is a Borel subgroup. Let
![]() ${\mathbf T}$
be a maximal torus contained in
${\mathbf T}$
be a maximal torus contained in
![]() ${\mathbf B}$
, and
${\mathbf B}$
, and
![]() ${\mathbf U}=R_u({\mathbf B})$
be the unipotent radical of
${\mathbf U}=R_u({\mathbf B})$
be the unipotent radical of
![]() ${\mathbf B}$
. We identify
${\mathbf B}$
. We identify
![]() ${\mathbf G}$
with
${\mathbf G}$
with
![]() ${\mathbf G}(\Bbbk )$
and do likewise for various subgroups of
${\mathbf G}(\Bbbk )$
and do likewise for various subgroups of
![]() ${\mathbf G}$
such as
${\mathbf G}$
such as
![]() ${\mathbf B}, {\mathbf T}, {\mathbf U}$
${\mathbf B}, {\mathbf T}, {\mathbf U}$
![]() $\cdots $
. We denote by
$\cdots $
. We denote by
![]() $\Phi =\Phi ({\mathbf G};{\mathbf T})$
the corresponding root system, and by
$\Phi =\Phi ({\mathbf G};{\mathbf T})$
the corresponding root system, and by
![]() $\Phi ^+$
(resp.
$\Phi ^+$
(resp.
![]() $\Phi ^-$
) the set of positive (resp. negative) roots determined by
$\Phi ^-$
) the set of positive (resp. negative) roots determined by
![]() ${\mathbf B}$
. Let
${\mathbf B}$
. Let
![]() $W=N_{\mathbf G}({\mathbf T})/{\mathbf T}$
be the corresponding Weyl group. We denote by
$W=N_{\mathbf G}({\mathbf T})/{\mathbf T}$
be the corresponding Weyl group. We denote by
![]() $\Delta =\{\alpha _i\mid i\in I\}$
the set of simple roots and by
$\Delta =\{\alpha _i\mid i\in I\}$
the set of simple roots and by
![]() $S=\{s_i:=s_{\alpha _i}\mid i\in I\}$
the corresponding simple reflections in W. For each
$S=\{s_i:=s_{\alpha _i}\mid i\in I\}$
the corresponding simple reflections in W. For each
![]() $\alpha \in \Phi $
, let
$\alpha \in \Phi $
, let
![]() ${\mathbf U}_\alpha $
be the root subgroup corresponding to
${\mathbf U}_\alpha $
be the root subgroup corresponding to
![]() $\alpha $
and we fix an isomorphism
$\alpha $
and we fix an isomorphism
![]() $\varepsilon _\alpha : \Bbbk \rightarrow {\mathbf U}_\alpha $
such that
$\varepsilon _\alpha : \Bbbk \rightarrow {\mathbf U}_\alpha $
such that
![]() $t\varepsilon _\alpha (c)t^{-1}=\varepsilon _\alpha (\alpha (t)c)$
for any
$t\varepsilon _\alpha (c)t^{-1}=\varepsilon _\alpha (\alpha (t)c)$
for any
![]() $t\in {\mathbf T}$
and
$t\in {\mathbf T}$
and
![]() $c\in \Bbbk $
. For any
$c\in \Bbbk $
. For any
![]() $w\in W$
, let
$w\in W$
, let
![]() ${\mathbf U}_w$
(resp.
${\mathbf U}_w$
(resp.
![]() ${\mathbf U}_w^{\prime }$
) be the subgroup of
${\mathbf U}_w^{\prime }$
) be the subgroup of
![]() ${\mathbf U}$
generated by all
${\mathbf U}$
generated by all
![]() ${\mathbf U}_\alpha $
with
${\mathbf U}_\alpha $
with
![]() $w(\alpha )\in \Phi ^-$
(resp.
$w(\alpha )\in \Phi ^-$
(resp.
![]() $w(\alpha )\in \Phi ^+$
). For any
$w(\alpha )\in \Phi ^+$
). For any
![]() $J\subset I$
, let
$J\subset I$
, let
![]() $W_J$
be the corresponding standard parabolic subgroup of W and
$W_J$
be the corresponding standard parabolic subgroup of W and
![]() $w_J$
be the longest element in
$w_J$
be the longest element in
![]() $W_J$
. For a subgroup H of
$W_J$
. For a subgroup H of
![]() $ {\mathbf G}$
and
$ {\mathbf G}$
and
![]() $g\in {\mathbf G}$
, let
$g\in {\mathbf G}$
, let
![]() $H^{g}= g^{-1}H g$
.
$H^{g}= g^{-1}H g$
.
The permutation module
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
is isomorphic to the induced module
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
is isomorphic to the induced module
![]() $\mathbb {M}(\operatorname {tr})= \mathbb {F} {\mathbf G} \otimes _{\mathbb {F} \mathbf B} \text {tr}$
. Now let
$\mathbb {M}(\operatorname {tr})= \mathbb {F} {\mathbf G} \otimes _{\mathbb {F} \mathbf B} \text {tr}$
. Now let
![]() ${\mathbf 1}_{tr}$
be a nonzero element of
${\mathbf 1}_{tr}$
be a nonzero element of
![]() $\operatorname {tr}$
. For convenience, we abbreviate
$\operatorname {tr}$
. For convenience, we abbreviate
![]() $x\otimes {\mathbf 1}_{\operatorname {tr}}\in \mathbb {M}(\operatorname {tr})$
to
$x\otimes {\mathbf 1}_{\operatorname {tr}}\in \mathbb {M}(\operatorname {tr})$
to
![]() $x{\mathbf 1}_{\operatorname {tr}}$
. Each element
$x{\mathbf 1}_{\operatorname {tr}}$
. Each element
![]() $\varphi \in \operatorname {End}_{\mathbb {F}{\mathbf G}}(\mathbb {M}(\operatorname {tr}))$
is determined by
$\varphi \in \operatorname {End}_{\mathbb {F}{\mathbf G}}(\mathbb {M}(\operatorname {tr}))$
is determined by
![]() $\varphi ({\mathbf 1}_{tr})$
. Note that
$\varphi ({\mathbf 1}_{tr})$
. Note that
![]() $\varphi ({\mathbf 1}_{tr})$
is a
$\varphi ({\mathbf 1}_{tr})$
is a
![]() ${\mathbf B}$
-stable vector. Thus we have
${\mathbf B}$
-stable vector. Thus we have
![]() $\varphi ({\mathbf 1}_{tr})= \lambda {\mathbf 1}_{tr}$
for some
$\varphi ({\mathbf 1}_{tr})= \lambda {\mathbf 1}_{tr}$
for some
![]() $\lambda \in \mathbb {F}$
, which implies that
$\lambda \in \mathbb {F}$
, which implies that
![]() $\operatorname {End}_{\mathbb {F}{\mathbf G}}(\mathbb {M}(\operatorname {tr}))\cong \mathbb {F} $
. In particular, the
$\operatorname {End}_{\mathbb {F}{\mathbf G}}(\mathbb {M}(\operatorname {tr}))\cong \mathbb {F} $
. In particular, the
![]() $\mathbb {F} {\mathbf G}$
-module
$\mathbb {F} {\mathbf G}$
-module
![]() $\mathbb {M}(\operatorname {tr})$
is indecomposable.
$\mathbb {M}(\operatorname {tr})$
is indecomposable.
For any
![]() $w\in W$
, let
$w\in W$
, let
![]() $\dot {w}$
be a representative of w. For any
$\dot {w}$
be a representative of w. For any
![]() $t\in {\mathbf T}$
and
$t\in {\mathbf T}$
and
![]() $n\in N_{\mathbf G}({\mathbf T})$
, we have
$n\in N_{\mathbf G}({\mathbf T})$
, we have
![]() $nt {\mathbf 1}_{\operatorname {tr}}= n {\mathbf 1}_{\operatorname {tr}}$
. Thus
$nt {\mathbf 1}_{\operatorname {tr}}= n {\mathbf 1}_{\operatorname {tr}}$
. Thus
![]() $w {\mathbf 1}_{\operatorname {tr}}=\dot {w} {\mathbf 1}_{\operatorname {tr}}$
is well-defined. For any
$w {\mathbf 1}_{\operatorname {tr}}=\dot {w} {\mathbf 1}_{\operatorname {tr}}$
is well-defined. For any
![]() $J\subset I$
, we set
$J\subset I$
, we set
 $$ \begin{align*}\eta_J=\sum_{w\in W_J}(-1)^{\ell(w)}w {\mathbf 1}_{\operatorname{tr}},\end{align*} $$
$$ \begin{align*}\eta_J=\sum_{w\in W_J}(-1)^{\ell(w)}w {\mathbf 1}_{\operatorname{tr}},\end{align*} $$
where
![]() $\ell (w)$
is the length of w. Let
$\ell (w)$
is the length of w. Let
![]() $\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf G}\eta _J$
. It was proved in [Reference Xi8, Prop. 2.3] that
$\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf G}\eta _J$
. It was proved in [Reference Xi8, Prop. 2.3] that
![]() $\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf U}W\eta _J.$
For
$\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf U}W\eta _J.$
For
![]() $w\in W$
, we set
$w\in W$
, we set
For any subset
![]() $J\subset I$
, we let
$J\subset I$
, we let
Proposition 2.1. For any
![]() $J\subset I$
, the
$J\subset I$
, the
![]() $\mathbb {F} {\mathbf G}$
-module
$\mathbb {F} {\mathbf G}$
-module
![]() $\mathbb {M}(\operatorname {tr})_J$
has the form
$\mathbb {M}(\operatorname {tr})_J$
has the form
 $$ \begin{align*}\mathbb{M}(\operatorname{tr})_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}w\eta_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}_{w_Jw^{-1}}w\eta_J,\end{align*} $$
$$ \begin{align*}\mathbb{M}(\operatorname{tr})_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}w\eta_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}_{w_Jw^{-1}}w\eta_J,\end{align*} $$
and the set
![]() $\{uw\eta _J \mid w\in X_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
$\{uw\eta _J \mid w\in X_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
![]() $\mathbb {M}(\operatorname {tr})_J$
.
$\mathbb {M}(\operatorname {tr})_J$
.
Proof. First, it is easy to see that
![]() $\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf U}W\eta _J= \mathbb {F}{\mathbf U}X_J\eta _J$
since
$\mathbb {M}(\operatorname {tr})_J=\mathbb {F}{\mathbf U}W\eta _J= \mathbb {F}{\mathbf U}X_J\eta _J$
since
![]() $y\eta _J= (-1)^{\ell (y)} \eta _J$
for any
$y\eta _J= (-1)^{\ell (y)} \eta _J$
for any
![]() $y\in W_J$
. Let
$y\in W_J$
. Let
![]() $w\in X_J$
. For any
$w\in X_J$
. For any
![]() $\gamma \in \Phi ^+$
such that
$\gamma \in \Phi ^+$
such that
![]() $w_Jw^{-1}(\gamma ) \in \Phi ^+ $
, we have
$w_Jw^{-1}(\gamma ) \in \Phi ^+ $
, we have
![]() $x^{-1}w^{-1}(\gamma ) \in \Phi ^+$
for any
$x^{-1}w^{-1}(\gamma ) \in \Phi ^+$
for any
![]() $x\in W_J$
. For
$x\in W_J$
. For
![]() $u\in {\mathbf U}_{\gamma }$
and
$u\in {\mathbf U}_{\gamma }$
and
![]() $x\in W_J$
, we get
$x\in W_J$
, we get
since
![]() $x^{-1}w^{-1} u w x\in {\mathbf U}$
. In particular, we get
$x^{-1}w^{-1} u w x\in {\mathbf U}$
. In particular, we get
![]() ${\mathbf U}w\eta _J= {\mathbf U}_{w_Jw^{-1}}w\eta _J$
. Then we obtain the first part.
${\mathbf U}w\eta _J= {\mathbf U}_{w_Jw^{-1}}w\eta _J$
. Then we obtain the first part.
In the following, we show that
![]() $\{uw\eta _J \mid w\in X_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
$\{uw\eta _J \mid w\in X_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
![]() $\mathbb {M}(\operatorname {tr})_J$
. It is enough to prove that this set is linearly independent. Suppose this set is linearly dependent, then there exist
$\mathbb {M}(\operatorname {tr})_J$
. It is enough to prove that this set is linearly independent. Suppose this set is linearly dependent, then there exist
![]() $f_{u,w}\in \mathbb {F}$
(not all zero) such that
$f_{u,w}\in \mathbb {F}$
(not all zero) such that
 $$ \begin{align} \sum_{w\in X_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uw\eta_J=0. \end{align} $$
$$ \begin{align} \sum_{w\in X_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uw\eta_J=0. \end{align} $$
Let
![]() $z\in X_J$
whose length is maximal such that
$z\in X_J$
whose length is maximal such that
![]() $f_{u_0,z}\ne 0$
for some
$f_{u_0,z}\ne 0$
for some
![]() $u_0\in {\mathbf U}_{{w_J}z^{-1}}$
. Substitute
$u_0\in {\mathbf U}_{{w_J}z^{-1}}$
. Substitute
 $\eta _J=\displaystyle \sum _{x\in W_J}(-1)^{\ell (x)}x {\mathbf 1}_{\operatorname {tr}} $
in the equation (2.1). According to the Bruhat decomposition, the set
$\eta _J=\displaystyle \sum _{x\in W_J}(-1)^{\ell (x)}x {\mathbf 1}_{\operatorname {tr}} $
in the equation (2.1). According to the Bruhat decomposition, the set
![]() $\{uw{\mathbf 1}_{\operatorname {tr}} \mid w\in W, u\in {\mathbf U}_{w^{-1}} \}$
is linearly independent in
$\{uw{\mathbf 1}_{\operatorname {tr}} \mid w\in W, u\in {\mathbf U}_{w^{-1}} \}$
is linearly independent in
![]() $\mathbb {M}(\operatorname {tr})$
. Then we have
$\mathbb {M}(\operatorname {tr})$
. Then we have
 $\displaystyle \sum _{u\in {\mathbf U}_{{w_J}z^{-1}} } f_{u, z} uzw_J{\mathbf 1}_{\operatorname {tr}}=0.$
So we get
$\displaystyle \sum _{u\in {\mathbf U}_{{w_J}z^{-1}} } f_{u, z} uzw_J{\mathbf 1}_{\operatorname {tr}}=0.$
So we get
![]() $f_{u,z}=0$
for all
$f_{u,z}=0$
for all
![]() $u\in {\mathbf U}_{{w_J}z^{-1}}$
, which is a contradiction. The proposition is proved.
$u\in {\mathbf U}_{{w_J}z^{-1}}$
, which is a contradiction. The proposition is proved.
For any
![]() $i\in I$
, set
$i\in I$
, set
![]() $ {\mathbf U}_{\alpha _i}^*= {\mathbf U}_{\alpha _i}\backslash \{id\}$
, where
$ {\mathbf U}_{\alpha _i}^*= {\mathbf U}_{\alpha _i}\backslash \{id\}$
, where
![]() $id$
is the neutral element of
$id$
is the neutral element of
![]() $ {\mathbf U}$
. For the convenience of later discussion, we give some details about the expression of the element
$ {\mathbf U}$
. For the convenience of later discussion, we give some details about the expression of the element
![]() $\dot {s_i} u_i w \eta _J $
, where
$\dot {s_i} u_i w \eta _J $
, where
![]() $u_i\in {\mathbf U}_{\alpha _i}^*$
and
$u_i\in {\mathbf U}_{\alpha _i}^*$
and
![]() $w\in X_J$
. For each
$w\in X_J$
. For each
![]() $u_i\in {\mathbf U}_{\alpha _i}^*$
, we have
$u_i\in {\mathbf U}_{\alpha _i}^*$
, we have
where
![]() $f_i(u_i),g_i(u_i) \in {\mathbf U}_{\alpha _i}^*$
, and
$f_i(u_i),g_i(u_i) \in {\mathbf U}_{\alpha _i}^*$
, and
![]() $h_i(u_i)\in {\mathbf T}$
are uniquely determined. Moreover, if we regard
$h_i(u_i)\in {\mathbf T}$
are uniquely determined. Moreover, if we regard
![]() $f_i$
as a morphism on
$f_i$
as a morphism on
![]() ${\mathbf U}_{\alpha _i}^*$
, then
${\mathbf U}_{\alpha _i}^*$
, then
![]() $f_i$
is a bijection. The following lemma is very useful in the later discussion. Its proof can be found in the proof of [Reference Xi8, Prop. 2.3] and we omit it.
$f_i$
is a bijection. The following lemma is very useful in the later discussion. Its proof can be found in the proof of [Reference Xi8, Prop. 2.3] and we omit it.
Lemma 2.2. Let
![]() $u_i\in {\mathbf U}_{\alpha _i}^* $
, with the notation above, then we have
$u_i\in {\mathbf U}_{\alpha _i}^* $
, with the notation above, then we have
(a) If
![]() $ww_J\leq s_iww_J$
, then
$ww_J\leq s_iww_J$
, then
![]() $\dot {s_i} u_i w\eta _J =s_iw \eta _J $
.
$\dot {s_i} u_i w\eta _J =s_iw \eta _J $
.
(b) If
![]() $s_i w \leq w$
, then
$s_i w \leq w$
, then
![]() $\dot {s_i} u_i w \eta _J = f_i(u_i)w\eta _J$
.
$\dot {s_i} u_i w \eta _J = f_i(u_i)w\eta _J$
.
(c) If
![]() $w \leq s_iw$
but
$w \leq s_iw$
but
![]() $s_iww_J\leq ww_J$
, then
$s_iww_J\leq ww_J$
, then
![]() $\dot {s_i} u_i w \eta _J =(f_i(u_i)-1)w\eta _J $
.
$\dot {s_i} u_i w \eta _J =(f_i(u_i)-1)w\eta _J $
.
Following [Reference Xi8, 2.6], we define
where
![]() $\mathbb {M}(\operatorname {tr})_J^{\prime }$
is the sum of all
$\mathbb {M}(\operatorname {tr})_J^{\prime }$
is the sum of all
![]() $\mathbb {M}(\operatorname {tr})_K$
with
$\mathbb {M}(\operatorname {tr})_K$
with
![]() $J\subsetneq K$
. We denote by
$J\subsetneq K$
. We denote by
![]() $C_J$
the image of
$C_J$
the image of
![]() $\eta _J$
in
$\eta _J$
in
![]() $E_J$
. For each
$E_J$
. For each
![]() $w\in W$
, let
$w\in W$
, let
 $$ \begin{align*}h_w=\sum_{y\leq w}(-1)^{\ell(w)-\ell(y)}P_{y,w}(1)y\in \mathbb{F} W,\end{align*} $$
$$ \begin{align*}h_w=\sum_{y\leq w}(-1)^{\ell(w)-\ell(y)}P_{y,w}(1)y\in \mathbb{F} W,\end{align*} $$
where
![]() $P_{y,w}$
are Kazhdan-Lusztig polynomials (see [Reference Kazhdan and Lusztig5, Th. 1.1]). The set
$P_{y,w}$
are Kazhdan-Lusztig polynomials (see [Reference Kazhdan and Lusztig5, Th. 1.1]). The set
![]() $\{h_w\mid w\in W\}$
is a basis of
$\{h_w\mid w\in W\}$
is a basis of
![]() $ \mathbb {F} W$
. We set
$ \mathbb {F} W$
. We set
Lemma 2.3. Let
![]() $J\subset I$
. Then each one of the following sets is a basis of
$J\subset I$
. Then each one of the following sets is a basis of
![]() $\mathbb {F} Wh_{w_J}$
:
$\mathbb {F} Wh_{w_J}$
:
(a)
![]() $\{wh_{w_J}\mid w\in X_J\}$
;
$\{wh_{w_J}\mid w\in X_J\}$
;
(b)
![]() $\{h_{ww_J}\mid w\in X_J\}$
;
$\{h_{ww_J}\mid w\in X_J\}$
;
(c)
![]() $\{yh_{w_J}\mid y\in Y_J\}\cup \{h_{xw_J}\mid x\in X_J\backslash Y_J\}$
.
$\{yh_{w_J}\mid y\in Y_J\}\cup \{h_{xw_J}\mid x\in X_J\backslash Y_J\}$
.
Proof. (a) By [Reference Kazhdan and Lusztig5, Lem. 2.6(vi)], we see that
 $$ \begin{align*}h_{w_J}=(-1)^{\ell(w_J)} \sum_{y\in W_J} (-1)^{\ell(y)}y \in \mathbb{F} W.\end{align*} $$
$$ \begin{align*}h_{w_J}=(-1)^{\ell(w_J)} \sum_{y\in W_J} (-1)^{\ell(y)}y \in \mathbb{F} W.\end{align*} $$
It is clear that
![]() $wh_{w_J}=(-1)^{\ell (w)}h_{w_J} $
for any
$wh_{w_J}=(-1)^{\ell (w)}h_{w_J} $
for any
![]() $w\in W_J$
. So we have
$w\in W_J$
. So we have
![]() $\mathbb {F} Wh_{w_J}=\mathbb {F} X_Jh_{w_J}$
. Now suppose that there exist
$\mathbb {F} Wh_{w_J}=\mathbb {F} X_Jh_{w_J}$
. Now suppose that there exist
![]() $a_w\in \mathbb {F}$
(not all zero) such that
$a_w\in \mathbb {F}$
(not all zero) such that
 $\displaystyle \sum _{w\in X_J} a_w wh_{w_J}=0.$
Let
$\displaystyle \sum _{w\in X_J} a_w wh_{w_J}=0.$
Let
![]() $z\in X_J$
whose length is maximal such that
$z\in X_J$
whose length is maximal such that
![]() $a_z\ne 0$
. Substitute
$a_z\ne 0$
. Substitute
![]() $h_{w_J}$
and we get
$h_{w_J}$
and we get
![]() $a_zww_J=0$
in
$a_zww_J=0$
in
![]() $\mathbb {F} W$
. So
$\mathbb {F} W$
. So
![]() $a_z=0$
, which is a contraction. Therefore,
$a_z=0$
, which is a contraction. Therefore,
![]() $\{wh_{w_J}\mid w\in X_J\}$
is a basis of
$\{wh_{w_J}\mid w\in X_J\}$
is a basis of
![]() $\mathbb {F} Wh_{w_J}$
.
$\mathbb {F} Wh_{w_J}$
.
(b) By [Reference Geck4, Lem. 2.8(c)], for
![]() $x\in X_J$
, we have
$x\in X_J$
, we have
 $$ \begin{align} h_{xw_J}=xh_{w_J}+ \sum_{ w\in X_J, w<x}b_wwh_{w_J}, \quad b_w\in \mathbb{F}. \end{align} $$
$$ \begin{align} h_{xw_J}=xh_{w_J}+ \sum_{ w\in X_J, w<x}b_wwh_{w_J}, \quad b_w\in \mathbb{F}. \end{align} $$
Using induction on
![]() $\ell (x)$
we see that
$\ell (x)$
we see that
 $$ \begin{align} xh_{w_J}=h_{xw_J} + \sum_{ w\in X_J, w<x}b^{\prime}_wh_{ww_J}, \quad b^{\prime}_w\in \mathbb{F}. \end{align} $$
$$ \begin{align} xh_{w_J}=h_{xw_J} + \sum_{ w\in X_J, w<x}b^{\prime}_wh_{ww_J}, \quad b^{\prime}_w\in \mathbb{F}. \end{align} $$
Thus (b) is proved by (a).
(c) We claim that for any
![]() $w\in X_J$
,
$w\in X_J$
,
![]() $wh_{w_J}$
is a linear combination of the elements in
$wh_{w_J}$
is a linear combination of the elements in
![]() $\{yh_{w_J}\mid y\in Y_J\}\cup \{h_{xw_J}\mid x\in X_J\backslash Y_J\}$
. If
$\{yh_{w_J}\mid y\in Y_J\}\cup \{h_{xw_J}\mid x\in X_J\backslash Y_J\}$
. If
![]() $\ell (w)=0,$
then the claim is obvious. Now assume that the claim is true for
$\ell (w)=0,$
then the claim is obvious. Now assume that the claim is true for
![]() $z\in X_J$
with
$z\in X_J$
with
![]() $\ell (z)<\ell (w)$
. If
$\ell (z)<\ell (w)$
. If
![]() $w\in Y_J$
, then the claim is clear. If
$w\in Y_J$
, then the claim is clear. If
![]() $w\in X_J\backslash Y_J$
, using formula (2.3) and induction hypothesis, we see that the claim is true. Now (c) is proved.
$w\in X_J\backslash Y_J$
, using formula (2.3) and induction hypothesis, we see that the claim is true. Now (c) is proved.
Proposition 2.4. For
![]() $J\subset I$
, we have
$J\subset I$
, we have
 $$ \begin{align*}E_J=\sum_{w\in Y_J} \mathbb{F} {\mathbf U}_{w_Jw^{-1}}wC_J,\end{align*} $$
$$ \begin{align*}E_J=\sum_{w\in Y_J} \mathbb{F} {\mathbf U}_{w_Jw^{-1}}wC_J,\end{align*} $$
and the set
![]() $\{uwC_J \mid w\in Y_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
$\{uwC_J \mid w\in Y_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
forms a basis of
![]() $E_J$
.
$E_J$
.
Proof. For
![]() $w\in W$
, we set
$w\in W$
, we set
![]() $h^{\prime }_w=h_w {\mathbf 1}_{\operatorname {tr}}\in \mathbb {M}(\operatorname {tr})$
. Thus,
$h^{\prime }_w=h_w {\mathbf 1}_{\operatorname {tr}}\in \mathbb {M}(\operatorname {tr})$
. Thus,
![]() $h^{\prime }_{w_J} =(-1)^{\ell (w_J)}\eta _J$
for any
$h^{\prime }_{w_J} =(-1)^{\ell (w_J)}\eta _J$
for any
![]() $J\subset I$
by [Reference Kazhdan and Lusztig5, Lem. 2.6(vi)]. According to Lemma 2.3 (c), we get
$J\subset I$
by [Reference Kazhdan and Lusztig5, Lem. 2.6(vi)]. According to Lemma 2.3 (c), we get
 $$ \begin{align*}\mathbb{M}(\operatorname{tr})_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}w\eta_J= \sum_{w\in Y_J}\mathbb{F}{\mathbf U}w\eta_J+ \sum_{x\in X_J \setminus Y_J}\mathbb{F}{\mathbf U}h^{\prime}_{xw_J}.\end{align*} $$
$$ \begin{align*}\mathbb{M}(\operatorname{tr})_J=\sum_{w\in X_J}\mathbb{F}{\mathbf U}w\eta_J= \sum_{w\in Y_J}\mathbb{F}{\mathbf U}w\eta_J+ \sum_{x\in X_J \setminus Y_J}\mathbb{F}{\mathbf U}h^{\prime}_{xw_J}.\end{align*} $$
We claim that
 $\mathbb {M}(\operatorname {tr})_J^{\prime }=\displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} $
. For
$\mathbb {M}(\operatorname {tr})_J^{\prime }=\displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} $
. For
![]() $x\in X_J \setminus Y_J$
, we see that
$x\in X_J \setminus Y_J$
, we see that
![]() $\mathscr {R}(xw_J)=K$
for some
$\mathscr {R}(xw_J)=K$
for some
![]() $K \supsetneq J$
. Thus
$K \supsetneq J$
. Thus
![]() $xw_J=yw_K$
for some
$xw_J=yw_K$
for some
![]() $y\in X_K$
. By Lemma 2.3 (b), we have
$y\in X_K$
. By Lemma 2.3 (b), we have
![]() $ h^{\prime }_{xw_J}= h^{\prime }_{yw_K} \in \mathbb {F} W\eta _K$
which implies
$ h^{\prime }_{xw_J}= h^{\prime }_{yw_K} \in \mathbb {F} W\eta _K$
which implies
 $ \displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} \subseteq \mathbb {M}(\operatorname {tr})_J^{\prime }$
. On the other hand, we see that
$ \displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} \subseteq \mathbb {M}(\operatorname {tr})_J^{\prime }$
. On the other hand, we see that
![]() $X_K \subseteq X_J\backslash Y_J$
for any
$X_K \subseteq X_J\backslash Y_J$
for any
![]() $K \supsetneq J$
. Therefore we get
$K \supsetneq J$
. Therefore we get
 $\mathbb {M}(\operatorname {tr})_K \subseteq \displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J}$
for any
$\mathbb {M}(\operatorname {tr})_K \subseteq \displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J}$
for any
![]() $K \supsetneq J$
. The claim is proved and we get
$K \supsetneq J$
. The claim is proved and we get
 $$ \begin{align*}E_J=\mathbb{M}(\operatorname{tr})_J/\mathbb{M}(\operatorname{tr})_J^{\prime}= \sum_{w\in Y_J} \mathbb{F} {\mathbf U} wC_J.\end{align*} $$
$$ \begin{align*}E_J=\mathbb{M}(\operatorname{tr})_J/\mathbb{M}(\operatorname{tr})_J^{\prime}= \sum_{w\in Y_J} \mathbb{F} {\mathbf U} wC_J.\end{align*} $$
It is not difficult to see that
![]() $ {\mathbf U} wC_J= {\mathbf U}_{w_Jw^{-1}}wC_J$
for any
$ {\mathbf U} wC_J= {\mathbf U}_{w_Jw^{-1}}wC_J$
for any
![]() $w\in Y_J$
. Thus, we obtain the first part.
$w\in Y_J$
. Thus, we obtain the first part.
Now we show that the set
![]() $\{uwC_J \mid w\in Y_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
is a basis of
$\{uwC_J \mid w\in Y_J, u\in {\mathbf U}_{w_Jw^{-1}} \}$
is a basis of
![]() $E_J$
. It is enough to prove that this set is linearly independent. Suppose that this set is linearly dependent. Then there exist
$E_J$
. It is enough to prove that this set is linearly independent. Suppose that this set is linearly dependent. Then there exist
![]() $f_{u, w} \in \mathbb {F}$
(not all zero) such that
$f_{u, w} \in \mathbb {F}$
(not all zero) such that
 $$ \begin{align*}\sum_{w\in Y_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uwC_J=0.\end{align*} $$
$$ \begin{align*}\sum_{w\in Y_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uwC_J=0.\end{align*} $$
Noting that
![]() $E_J=\mathbb {M}(\operatorname {tr})_J/\mathbb {M}(\operatorname {tr})_J^{\prime }$
, we have
$E_J=\mathbb {M}(\operatorname {tr})_J/\mathbb {M}(\operatorname {tr})_J^{\prime }$
, we have
 $$ \begin{align*}\sum_{w\in Y_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uw\eta_J \in \mathbb{M}(\operatorname{tr})_J^{\prime}.\end{align*} $$
$$ \begin{align*}\sum_{w\in Y_J} \sum_{u\in {\mathbf U}_{w_Jw^{-1}} } f_{u, w} uw\eta_J \in \mathbb{M}(\operatorname{tr})_J^{\prime}.\end{align*} $$
Without loss of generality, we assume that
![]() $u_0=id$
for some
$u_0=id$
for some
![]() $z\in Y_J$
with
$z\in Y_J$
with
![]() $f_{u_0,z} \ne 0$
. Note that the
$f_{u_0,z} \ne 0$
. Note that the
![]() ${\mathbf T}$
-fixed subspace of
${\mathbf T}$
-fixed subspace of
![]() $\mathbb {M}(\operatorname {tr})_J$
is
$\mathbb {M}(\operatorname {tr})_J$
is
 $\displaystyle \sum _{w\in X_J} \mathbb {F}w\eta _J $
. Since
$\displaystyle \sum _{w\in X_J} \mathbb {F}w\eta _J $
. Since
![]() $z\eta _J$
is a
$z\eta _J$
is a
![]() ${\mathbf T}$
-stable vector and
${\mathbf T}$
-stable vector and
 $\mathbb {M}(\operatorname {tr})_J^{\prime }=\displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} $
, it is not difficult to see that
$\mathbb {M}(\operatorname {tr})_J^{\prime }=\displaystyle \sum _{x\in X_J \setminus Y_J}\mathbb {F}{\mathbf U}h^{\prime }_{xw_J} $
, it is not difficult to see that
![]() $z\eta _J$
is a linear combination of the following set
$z\eta _J$
is a linear combination of the following set
This is a contradiction by Lemma 2.3 (c). The proposition is proved.
Proposition 2.5. [Reference Xi8, Prop. 2.7] If J and K are different subsets of I, then
![]() $E_J$
and
$E_J$
and
![]() $E_K$
are not isomorphic.
$E_K$
are not isomorphic.
By the definition of
![]() $E_J$
, there exists a filtration of submodules for
$E_J$
, there exists a filtration of submodules for
![]() $\mathbb {F}[{\mathbf G}/{\mathbf B}]$
whose subquotients are
$\mathbb {F}[{\mathbf G}/{\mathbf B}]$
whose subquotients are
![]() $E_J$
$E_J$
![]() $(J\subset I)$
. In the following of this paper, we prove the irreducibility of
$(J\subset I)$
. In the following of this paper, we prove the irreducibility of
![]() $E_J$
for any
$E_J$
for any
![]() $J\subset I$
. Combining Proposition 2.5, we get Theorem 1.1.
$J\subset I$
. Combining Proposition 2.5, we get Theorem 1.1.
3 Self-enclosed subgroups
This section contains some preliminaries and properties of unipotent groups that are useful in later discussion. As before, let
![]() ${\mathbf U}$
be the unipotent radical of the Borel subgroup
${\mathbf U}$
be the unipotent radical of the Borel subgroup
![]() ${\mathbf B}$
. For any
${\mathbf B}$
. For any
![]() $w\in W$
, we set
$w\in W$
, we set
As before,
![]() ${\mathbf U}_w$
(resp.
${\mathbf U}_w$
(resp.
![]() ${\mathbf U}_w^{\prime }$
) is the subgroup of
${\mathbf U}_w^{\prime }$
) is the subgroup of
![]() ${\mathbf U}$
generated by all
${\mathbf U}$
generated by all
![]() ${\mathbf U}_\alpha $
with
${\mathbf U}_\alpha $
with
![]() $\alpha \in \Phi _w^-$
(resp.
$\alpha \in \Phi _w^-$
(resp.
![]() $\alpha \in \Phi _w^+$
). The following properties are well known (see [Reference Carter1]).
$\alpha \in \Phi _w^+$
). The following properties are well known (see [Reference Carter1]).
(a) For
![]() $w\in W$
and any root
$w\in W$
and any root
![]() $\alpha \in \Phi $
, we have
$\alpha \in \Phi $
, we have
![]() $\dot {w}{\mathbf U}_\alpha \dot {w}^{-1}={\mathbf U}_{w(\alpha )}$
;
$\dot {w}{\mathbf U}_\alpha \dot {w}^{-1}={\mathbf U}_{w(\alpha )}$
;
(b)
![]() $ {\mathbf U}_w$
and
$ {\mathbf U}_w$
and
![]() ${\mathbf U}^{\prime }_w$
are subgroups of
${\mathbf U}^{\prime }_w$
are subgroups of
![]() ${\mathbf U}$
, and we have
${\mathbf U}$
, and we have
![]() $\dot {w}{\mathbf U}^{\prime }_w\dot {w}^{-1} \subset {\mathbf U}$
;
$\dot {w}{\mathbf U}^{\prime }_w\dot {w}^{-1} \subset {\mathbf U}$
;
(c) The multiplication map
![]() ${\mathbf U}_w\times {\mathbf U}_w^{\prime }\rightarrow {\mathbf U}$
is a bijection;
${\mathbf U}_w\times {\mathbf U}_w^{\prime }\rightarrow {\mathbf U}$
is a bijection;
(d) Let
![]() $\Phi ^+ =\{\delta _1, \delta _2, \dots , \delta _m\}$
. Then
$\Phi ^+ =\{\delta _1, \delta _2, \dots , \delta _m\}$
. Then
![]() ${\mathbf U}= {\mathbf U}_{\delta _1}{\mathbf U}_{\delta _2}\dots {\mathbf U}_{\delta _m}$
and each element
${\mathbf U}= {\mathbf U}_{\delta _1}{\mathbf U}_{\delta _2}\dots {\mathbf U}_{\delta _m}$
and each element
![]() $u \in {\mathbf U}$
is uniquely expressible in the form
$u \in {\mathbf U}$
is uniquely expressible in the form
![]() $u=u_1u_2\dots u_m$
with
$u=u_1u_2\dots u_m$
with
![]() $u_{i}\in {\mathbf U}_{\delta _i}$
;
$u_{i}\in {\mathbf U}_{\delta _i}$
;
(e) (Commutator relations) Given two positive roots
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, there exist a total ordering on
$\beta $
, there exist a total ordering on
![]() $\Phi ^+$
and integers
$\Phi ^+$
and integers
![]() $c^{mn}_{\alpha \beta }$
such that
$c^{mn}_{\alpha \beta }$
such that
 $$ \begin{align*}[\varepsilon_\alpha(a),\varepsilon_\beta(b)]:=\varepsilon_\alpha(a)\varepsilon_\beta(b)\varepsilon_\alpha(a)^{-1}\varepsilon_\beta(b)^{-1}= \underset{m,n>0}{\prod} \varepsilon_{m\alpha+n\beta}(c^{mn}_{\alpha \beta}a^mb^n),\end{align*} $$
$$ \begin{align*}[\varepsilon_\alpha(a),\varepsilon_\beta(b)]:=\varepsilon_\alpha(a)\varepsilon_\beta(b)\varepsilon_\alpha(a)^{-1}\varepsilon_\beta(b)^{-1}= \underset{m,n>0}{\prod} \varepsilon_{m\alpha+n\beta}(c^{mn}_{\alpha \beta}a^mb^n),\end{align*} $$
for all
![]() $a,b\in \Bbbk $
, where the product is over all integers
$a,b\in \Bbbk $
, where the product is over all integers
![]() $m,n>0$
such that
$m,n>0$
such that
![]() $m\alpha +n\beta \in \Phi ^{+}$
, taken according to the chosen ordering.
$m\alpha +n\beta \in \Phi ^{+}$
, taken according to the chosen ordering.
As before, let
![]() $\Phi ^+ =\{\delta _1, \delta _2, \dots , \delta _m\}$
and for an element
$\Phi ^+ =\{\delta _1, \delta _2, \dots , \delta _m\}$
and for an element
![]() $u\in {\mathbf U}$
, we have
$u\in {\mathbf U}$
, we have
![]() $u=x_1x_2\dots x_m$
with
$u=x_1x_2\dots x_m$
with
![]() $x_i\in {\mathbf U}_{\delta _i}$
. If we choose another order of
$x_i\in {\mathbf U}_{\delta _i}$
. If we choose another order of
![]() $\Phi ^+$
and write
$\Phi ^+$
and write
![]() $\Phi ^+=\{\delta ^{\prime }_1, \delta ^{\prime }_2, \dots , \delta ^{\prime }_m\}$
, we get another expression of u such that
$\Phi ^+=\{\delta ^{\prime }_1, \delta ^{\prime }_2, \dots , \delta ^{\prime }_m\}$
, we get another expression of u such that
![]() $u=y_1y_2\dots y_m$
with
$u=y_1y_2\dots y_m$
with
![]() $y_i\in {\mathbf U}_{\delta ^{\prime }_i}$
. If
$y_i\in {\mathbf U}_{\delta ^{\prime }_i}$
. If
![]() $\delta _i=\delta ^{\prime }_j =\alpha $
is a simple root, by the commutator relations of root subgroups, we get
$\delta _i=\delta ^{\prime }_j =\alpha $
is a simple root, by the commutator relations of root subgroups, we get
![]() $x_i=y_j$
which is called the
$x_i=y_j$
which is called the
![]() ${\mathbf U}_{\alpha }$
-component of u. Noting that the simple roots are
${\mathbf U}_{\alpha }$
-component of u. Noting that the simple roots are
![]() $\Delta =\{\alpha _1, \alpha _2, \dots , \alpha _n\}$
and each
$\Delta =\{\alpha _1, \alpha _2, \dots , \alpha _n\}$
and each
![]() $\gamma \in \Phi ^+$
can be written as
$\gamma \in \Phi ^+$
can be written as
 $\gamma =\displaystyle \sum _{i=1}^n k_i \alpha _i$
, we denote by
$\gamma =\displaystyle \sum _{i=1}^n k_i \alpha _i$
, we denote by
 $\text {ht}(\gamma )=\displaystyle \sum _{i=1}^n k_i$
the height of
$\text {ht}(\gamma )=\displaystyle \sum _{i=1}^n k_i$
the height of
![]() $\gamma $
. It is easy to see that
$\gamma $
. It is easy to see that
 $\displaystyle \prod _{\text {ht}(\gamma )\geq s} {\mathbf U}_{\gamma }$
is a subgroup of
$\displaystyle \prod _{\text {ht}(\gamma )\geq s} {\mathbf U}_{\gamma }$
is a subgroup of
![]() $\mathbf U$
for any fixed integer
$\mathbf U$
for any fixed integer
![]() $s\in \mathbb {N}$
by the commutator relations of root subgroups.
$s\in \mathbb {N}$
by the commutator relations of root subgroups.
Given an order “
![]() $\prec $
” on
$\prec $
” on
![]() $\Phi ^+$
, we list all the positive roots
$\Phi ^+$
, we list all the positive roots
![]() $\delta _1, \delta _2, \dots , and\ \delta _m$
with respect to this order such that
$\delta _1, \delta _2, \dots , and\ \delta _m$
with respect to this order such that
![]() $\delta _i \prec \delta _j$
when
$\delta _i \prec \delta _j$
when
![]() $i<j$
. For any
$i<j$
. For any
![]() $u\in {\mathbf U}$
, we have a unique expression in the form
$u\in {\mathbf U}$
, we have a unique expression in the form
![]() $u=u_1u_2\dots u_m$
with
$u=u_1u_2\dots u_m$
with
![]() $u_i\in {\mathbf U}_{\delta _i}$
. Let X be a subset of
$u_i\in {\mathbf U}_{\delta _i}$
. Let X be a subset of
![]() $\mathbf U$
, we denote by
$\mathbf U$
, we denote by
It is easy to see that
![]() $X\cap {\mathbf U}_{\delta _k} \subseteq X\cap _{\prec } {\mathbf U}_{\delta _k}$
. Now let H be a subgroup of
$X\cap {\mathbf U}_{\delta _k} \subseteq X\cap _{\prec } {\mathbf U}_{\delta _k}$
. Now let H be a subgroup of
![]() ${\mathbf U}$
, and we say that a subgroup
${\mathbf U}$
, and we say that a subgroup
![]() $H \subset \mathbf U$
is self-enclosed with respect to the order “
$H \subset \mathbf U$
is self-enclosed with respect to the order “
![]() $\prec $
” if
$\prec $
” if
If H is self-enclosed with respect to any order on
![]() $\Phi ^+$
, then we say that H is a self-enclosed subgroup of
$\Phi ^+$
, then we say that H is a self-enclosed subgroup of
![]() $\mathbf U$
.
$\mathbf U$
.
Let H be a self-enclosed subgroup of
![]() $\mathbf U$
. For each
$\mathbf U$
. For each
![]() $\gamma \in \Phi ^+$
, we set
$\gamma \in \Phi ^+$
, we set
![]() $H_{\gamma }=H \cap {\mathbf U}_{\gamma }$
. Then we have
$H_{\gamma }=H \cap {\mathbf U}_{\gamma }$
. Then we have
![]() $H= H_{\delta _1} H_{\delta _2}\dots H_{\delta _m}.$
For
$H= H_{\delta _1} H_{\delta _2}\dots H_{\delta _m}.$
For
![]() $w\in W$
, set
$w\in W$
, set
![]() $H_w= H\cap {\mathbf U}_w$
. Then it is easy to see that
$H_w= H\cap {\mathbf U}_w$
. Then it is easy to see that
![]() $H_w$
is also a self-enclosed subgroup, and we have
$H_w$
is also a self-enclosed subgroup, and we have
 $\displaystyle H_w= \prod _{\gamma \in \Phi ^{-}_w} H_{\gamma }$
.
$\displaystyle H_w= \prod _{\gamma \in \Phi ^{-}_w} H_{\gamma }$
.
Example 3.1. Suppose
![]() $\Bbbk =\bar {\mathbb {F}}_q$
and
$\Bbbk =\bar {\mathbb {F}}_q$
and
![]() $\{\delta _1, \delta _2, \dots , \delta _m\}$
are all the positive roots such that
$\{\delta _1, \delta _2, \dots , \delta _m\}$
are all the positive roots such that
![]() $\text {ht}(\delta _1)\leq \text {ht}(\delta _2) \leq \dots \leq \text {ht}(\delta _m)$
. Assume that
$\text {ht}(\delta _1)\leq \text {ht}(\delta _2) \leq \dots \leq \text {ht}(\delta _m)$
. Assume that
![]() ${\mathbf U}$
is defined over
${\mathbf U}$
is defined over
![]() $\mathbb {F}_q$
and let
$\mathbb {F}_q$
and let
![]() $U_{q^a}$
be the set of
$U_{q^a}$
be the set of
![]() $\mathbb {F}_{q^a}$
-points of
$\mathbb {F}_{q^a}$
-points of
![]() $\mathbf U$
. Given
$\mathbf U$
. Given
![]() $a_1, a_2,\dots , a_m \in \mathbb {N}$
such that
$a_1, a_2,\dots , a_m \in \mathbb {N}$
such that
![]() $a_i$
is divisible by
$a_i$
is divisible by
![]() $a_j$
for any
$a_j$
for any
![]() $i < j$
, we set
$i < j$
, we set
Then it is not difficult to check that H is a self-enclosed subgroup of
![]() $\mathbf U$
.
$\mathbf U$
.
Now let H be a subgroup of
![]() $\mathbf U$
. Let
$\mathbf U$
. Let
![]() ${\mathbf V}$
be a subgroup of
${\mathbf V}$
be a subgroup of
![]() ${\mathbf U}$
which has the form
${\mathbf U}$
which has the form
![]() ${\mathbf V}= {\mathbf U}_{\beta _1}{\mathbf U}_{\beta _2}\dots {\mathbf U}_{\beta _k}$
. We let
${\mathbf V}= {\mathbf U}_{\beta _1}{\mathbf U}_{\beta _2}\dots {\mathbf U}_{\beta _k}$
. We let
 $$ \begin{align*}{\mathbf U}= \displaystyle \bigcup_{x\in L} x {\mathbf V} \quad \text{and} \quad {\mathbf U}= \displaystyle \bigcup_{y\in R} {\mathbf V} y,\end{align*} $$
$$ \begin{align*}{\mathbf U}= \displaystyle \bigcup_{x\in L} x {\mathbf V} \quad \text{and} \quad {\mathbf U}= \displaystyle \bigcup_{y\in R} {\mathbf V} y,\end{align*} $$
where L (resp. R) is a set of the left (resp. right) coset representatives of
![]() ${\mathbf V}$
in
${\mathbf V}$
in
![]() ${\mathbf U}$
. Then we define the following two sets:
${\mathbf U}$
. Then we define the following two sets:
Proposition 3.2. Let H be a self-enclosed subgroup of
![]() $\mathbf U$
. Let
$\mathbf U$
. Let
![]() ${\mathbf V}$
be a subgroup of
${\mathbf V}$
be a subgroup of
![]() $\mathbf U$
with the form
$\mathbf U$
with the form
![]() ${\mathbf V}= {\mathbf U}_{\beta _1}{\mathbf U}_{\beta _2}\dots {\mathbf U}_{\beta _k}$
, where
${\mathbf V}= {\mathbf U}_{\beta _1}{\mathbf U}_{\beta _2}\dots {\mathbf U}_{\beta _k}$
, where
![]() $\beta _1, \beta _2, \dots , \beta _k\in \Phi ^+$
. Then we have
$\beta _1, \beta _2, \dots , \beta _k\in \Phi ^+$
. Then we have
Proof. We just prove that
![]() $H_{{\mathbf V}}= H \cap {\mathbf V}$
. It is clear that
$H_{{\mathbf V}}= H \cap {\mathbf V}$
. It is clear that
![]() $H \cap {\mathbf V} \subset H_{{\mathbf V}}$
. Noting that
$H \cap {\mathbf V} \subset H_{{\mathbf V}}$
. Noting that
![]() ${\mathbf V}$
is a subgroup of
${\mathbf V}$
is a subgroup of
![]() ${\mathbf U}$
, we denote
${\mathbf U}$
, we denote
Let
![]() $v\in H_{{\mathbf V}}$
. Thus, there exists
$v\in H_{{\mathbf V}}$
. Thus, there exists
![]() $h \in H$
such that
$h \in H$
such that
![]() $h=xv$
for some
$h=xv$
for some
![]() $x\in L$
. We write
$x\in L$
. We write
Since H is self-enclosed, we see that
![]() $v_{\beta _j}\in H \cap {\mathbf U}_{\beta _j}$
which implies that
$v_{\beta _j}\in H \cap {\mathbf U}_{\beta _j}$
which implies that
![]() $v\in H \cap {\mathbf V}$
. Therefore, we get
$v\in H \cap {\mathbf V}$
. Therefore, we get
![]() $H_{{\mathbf V}}= H \cap {\mathbf V}$
. Similarly, we have
$H_{{\mathbf V}}= H \cap {\mathbf V}$
. Similarly, we have
![]() ${}_{\mathbf V}H= H \cap {\mathbf V}$
. The proposition is proved.
${}_{\mathbf V}H= H \cap {\mathbf V}$
. The proposition is proved.
Now we consider the special case that
![]() $\Bbbk $
is a field of positive characteristic p. In this case, it is well known that all the finitely generated subgroups of
$\Bbbk $
is a field of positive characteristic p. In this case, it is well known that all the finitely generated subgroups of
![]() ${\mathbf U}$
are finite p-groups. We have the following lemma.
${\mathbf U}$
are finite p-groups. We have the following lemma.
Lemma 3.3. Let X be a finite subset of
![]() ${\mathbf U}$
. There exists a finite p-subgroup H of
${\mathbf U}$
. There exists a finite p-subgroup H of
![]() ${\mathbf U}$
such that
${\mathbf U}$
such that
![]() $H\supseteq X$
and H is self-enclosed.
$H\supseteq X$
and H is self-enclosed.
Proof. Let
![]() $\Phi ^+= \{\delta _1, \delta _2, \dots , \delta _m\}$
such that
$\Phi ^+= \{\delta _1, \delta _2, \dots , \delta _m\}$
such that
![]() $\text {ht}(\delta _1)\leq \text {ht}(\delta _2) \leq \dots \leq \text {ht}(\delta _m)$
. For each
$\text {ht}(\delta _1)\leq \text {ht}(\delta _2) \leq \dots \leq \text {ht}(\delta _m)$
. For each
![]() $1 \leq k \leq m $
, we set
$1 \leq k \leq m $
, we set
![]() $X_{k}= X\cap _{\prec } {\mathbf U}_{\delta _k}$
. Let
$X_{k}= X\cap _{\prec } {\mathbf U}_{\delta _k}$
. Let
![]() $H_1$
be the subgroup of
$H_1$
be the subgroup of
![]() ${\mathbf U}_{\delta _1}$
, which is generated by
${\mathbf U}_{\delta _1}$
, which is generated by
![]() $X_1$
. Now we define the subgroup
$X_1$
. Now we define the subgroup
![]() $H_k$
by recursive step. Suppose that
$H_k$
by recursive step. Suppose that
![]() $H_1, H_2,\dots , H_{k-1}$
are defined, we set
$H_1, H_2,\dots , H_{k-1}$
are defined, we set
and let
![]() $H_k$
be the subgroup of
$H_k$
be the subgroup of
![]() ${\mathbf U}_{\delta _k}$
, which is generated by
${\mathbf U}_{\delta _k}$
, which is generated by
![]() $X_k$
and
$X_k$
and
![]() $Y_k$
. Now we have a series of subgroups
$Y_k$
. Now we have a series of subgroups
![]() $ H_1, H_2, \dots , H_{m}$
and then we set
$ H_1, H_2, \dots , H_{m}$
and then we set
![]() $H= \langle H_1, H_2, \dots , H_{m}\rangle $
, which is a finitely generated subgroup of
$H= \langle H_1, H_2, \dots , H_{m}\rangle $
, which is a finitely generated subgroup of
![]() ${\mathbf U}$
. Thus H is a finite p-subgroup of
${\mathbf U}$
. Thus H is a finite p-subgroup of
![]() ${\mathbf U}$
, which contains X by its construction. Moreover, it is not difficult to check that H is a self-enclosed of
${\mathbf U}$
, which contains X by its construction. Moreover, it is not difficult to check that H is a self-enclosed of
![]() $\mathbf U$
using the commutator relations of root subgroups.
$\mathbf U$
using the commutator relations of root subgroups.
It is easy to verify that the intersection of two self-enclosed subgroups of
![]() ${\mathbf U}$
is also self-enclosed. For a finite subset X of
${\mathbf U}$
is also self-enclosed. For a finite subset X of
![]() ${\mathbf U}$
, there exists a minimal self-enclosed subgroup V containing X. In this case, we also say that V is the self-enclosed subgroup generated by X.
${\mathbf U}$
, there exists a minimal self-enclosed subgroup V containing X. In this case, we also say that V is the self-enclosed subgroup generated by X.
4 Nonvanishing property of the augmentation
In this section, we fix a subset
![]() $J\subset I$
. By Proposition 2.4, we have
$J\subset I$
. By Proposition 2.4, we have
 $$ \begin{align*}E_J=\bigoplus_{w\in Y_J} \mathbb{F} {\mathbf U}_{w_Jw^{-1}}w C_J,\end{align*} $$
$$ \begin{align*}E_J=\bigoplus_{w\in Y_J} \mathbb{F} {\mathbf U}_{w_Jw^{-1}}w C_J,\end{align*} $$
as
![]() $\mathbb {F}$
-vector space. For each
$\mathbb {F}$
-vector space. For each
![]() $w\in Y_J$
, we denote by
$w\in Y_J$
, we denote by
the projection of vector spaces and by
the augmentation (restricting on w) which takes the sum of the coefficients with respect to the natural basis, i.e., for
 $\xi = \displaystyle \sum _{x\in {\mathbf U}_{w_Jw^{-1}} } a_x x w C_J$
, we set
$\xi = \displaystyle \sum _{x\in {\mathbf U}_{w_Jw^{-1}} } a_x x w C_J$
, we set
 $\epsilon _w(\xi )= \displaystyle \sum _{x\in {\mathbf U}_{w_Jw^{-1}} } a_x$
. Now we denote by
$\epsilon _w(\xi )= \displaystyle \sum _{x\in {\mathbf U}_{w_Jw^{-1}} } a_x$
. Now we denote by
 $$ \begin{align*}\epsilon= \bigoplus_{w\in Y_J} \epsilon_w \mathfrak{P}_w: E_J \rightarrow \mathbb{F}^{|Y_J|,}\end{align*} $$
$$ \begin{align*}\epsilon= \bigoplus_{w\in Y_J} \epsilon_w \mathfrak{P}_w: E_J \rightarrow \mathbb{F}^{|Y_J|,}\end{align*} $$
the augmentation on
![]() $E_J$
.
$E_J$
.
When considering the irreducibility of Steinberg module, the nonvanishing property of the augmentation is very crucial (see [Reference Yang9, Lem. 2.5] and [Reference Putman and Snowden6, Prop. 1.6]). In this section, we show that the non-vanishing property also holds for the augmentation
![]() $\epsilon $
defined above. Firstly we have the following lemma.
$\epsilon $
defined above. Firstly we have the following lemma.
Lemma 4.1. Let
![]() $\xi \in E_J $
be a nonzero element. Then there exists
$\xi \in E_J $
be a nonzero element. Then there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $\mathfrak {P}_e(g\xi )$
is nonzero.
$\mathfrak {P}_e(g\xi )$
is nonzero.
Proof. By Proposition 2.4,
![]() $\xi \in E_J $
has the following expression
$\xi \in E_J $
has the following expression
 $$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J.\end{align*} $$
$$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J.\end{align*} $$
Then there exists an element
![]() $h\in W$
with minimal length such that
$h\in W$
with minimal length such that
![]() $a_{h,x}\ne 0$
for some
$a_{h,x}\ne 0$
for some
![]() $x\in {\mathbf U}_{w_Jh^{-1}}$
, which implies that
$x\in {\mathbf U}_{w_Jh^{-1}}$
, which implies that
![]() $\mathfrak {P}_h(\xi )$
is nonzero. When
$\mathfrak {P}_h(\xi )$
is nonzero. When
![]() $h=e$
, the lemma is proved. Now suppose that
$h=e$
, the lemma is proved. Now suppose that
![]() $\ell (h)\geq 1$
, so there is a simple reflection s such that
$\ell (h)\geq 1$
, so there is a simple reflection s such that
![]() $\sigma =sh< h$
. Without loss of generality, we can assume that
$\sigma =sh< h$
. Without loss of generality, we can assume that
![]() $a_{h,id}\ne 0$
. We claim that either
$a_{h,id}\ne 0$
. We claim that either
![]() $\mathfrak {P}_{\sigma }(\dot {s} \xi ) $
is nonzero or
$\mathfrak {P}_{\sigma }(\dot {s} \xi ) $
is nonzero or
![]() $\mathfrak {P}_{\sigma }(\dot {s}y \xi )$
is nonzero for some
$\mathfrak {P}_{\sigma }(\dot {s}y \xi )$
is nonzero for some
![]() $y \in {\mathbf U}_s$
.
$y \in {\mathbf U}_s$
.
If
![]() $\mathfrak {P}_{\sigma }(\dot {s} \xi ) =0$
, then according to Lemma 2.2, there exists at least one element
$\mathfrak {P}_{\sigma }(\dot {s} \xi ) =0$
, then according to Lemma 2.2, there exists at least one element
![]() $v\in Y_J$
, which satisfies the following condition
$v\in Y_J$
, which satisfies the following condition
The subset of
![]() $Y_J$
whose elements satisfy this condition is also denoted by
$Y_J$
whose elements satisfy this condition is also denoted by
![]() $\spadesuit $
. Thus,
$\spadesuit $
. Thus,
![]() $\mathfrak {P}_{\sigma }(\dot {s} \xi ) =0$
tells us that
$\mathfrak {P}_{\sigma }(\dot {s} \xi ) =0$
tells us that
 $$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \mathfrak{P}_h(\xi))+ \mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(\xi))=0.\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \mathfrak{P}_h(\xi))+ \mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(\xi))=0.\end{align*} $$
In particular, we get
 $\displaystyle \mathfrak {P}_{\sigma }(\dot {s} \cdot \sum _{v\in \spadesuit }\mathfrak {P}_v(\xi )) \ne 0$
. Since
$\displaystyle \mathfrak {P}_{\sigma }(\dot {s} \cdot \sum _{v\in \spadesuit }\mathfrak {P}_v(\xi )) \ne 0$
. Since
![]() ${\mathbf U}$
is infinite, there exists infinitely many
${\mathbf U}$
is infinite, there exists infinitely many
![]() $y\in {\mathbf U}_s$
such that the
$y\in {\mathbf U}_s$
such that the
![]() $ {\mathbf U}_s$
-component of
$ {\mathbf U}_s$
-component of
![]() $yx$
is nontrivial for any x with
$yx$
is nontrivial for any x with
![]() $a_{h, x} \ne 0$
. For such an element y, we get
$a_{h, x} \ne 0$
. For such an element y, we get
![]() $\mathfrak {P}_{\sigma }(\dot {s} \cdot \mathfrak {P}_h(y\xi ))=0$
by Lemma 2.2 (b).
$\mathfrak {P}_{\sigma }(\dot {s} \cdot \mathfrak {P}_h(y\xi ))=0$
by Lemma 2.2 (b).
On the other hand, for
![]() $v\in \spadesuit $
and
$v\in \spadesuit $
and
![]() $a_{v,x}\ne 0$
, we see that the
$a_{v,x}\ne 0$
, we see that the
![]() $ {\mathbf U}_s$
-component of x is trivial, i.e.,
$ {\mathbf U}_s$
-component of x is trivial, i.e.,
![]() $ x\in {\mathbf U}^{\prime }_s$
. Note that
$ x\in {\mathbf U}^{\prime }_s$
. Note that
![]() ${\mathbf U}_{w_J \sigma ^{-1} s}={( {\mathbf U}_{w_J \sigma ^{-1}})}^{s} \cdot {\mathbf U}_s$
and
${\mathbf U}_{w_J \sigma ^{-1} s}={( {\mathbf U}_{w_J \sigma ^{-1}})}^{s} \cdot {\mathbf U}_s$
and
![]() $ {\mathbf U}^{\prime }_{w_J \sigma ^{-1}} = {({\mathbf U}^{\prime }_{w_J \sigma ^{-1}s})}^{s} \cdot {\mathbf U}_s$
. Then we can write
$ {\mathbf U}^{\prime }_{w_J \sigma ^{-1}} = {({\mathbf U}^{\prime }_{w_J \sigma ^{-1}s})}^{s} \cdot {\mathbf U}_s$
. Then we can write
Since this expression is unique, we can regard
![]() $p(-)$
and
$p(-)$
and
![]() $n(-)$
as functions on
$n(-)$
as functions on
![]() ${\mathbf U}^{\prime }_s$
. We let
${\mathbf U}^{\prime }_s$
. We let
![]() $yx= \omega _y(x)y$
, where
$yx= \omega _y(x)y$
, where
![]() $\omega _y(x) \in {\mathbf U}^{\prime }_s$
. Using the commutator relations of root subgroups, we can choose y such that
$\omega _y(x) \in {\mathbf U}^{\prime }_s$
. Using the commutator relations of root subgroups, we can choose y such that
![]() $n(\omega _y(x'))\ne n(\omega _y(x))$
unless
$n(\omega _y(x'))\ne n(\omega _y(x))$
unless
![]() $n(x)=n(x')$
since there are only finitely many
$n(x)=n(x')$
since there are only finitely many
![]() $x's$
satisfying
$x's$
satisfying
![]() $a_{v,x} \ne 0$
. Therefore, if we write
$a_{v,x} \ne 0$
. Therefore, if we write
 $$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(\xi))=\sum b_{\sigma,x} n(x)^{\dot{s}} \sigma C_J\ne 0,\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(\xi))=\sum b_{\sigma,x} n(x)^{\dot{s}} \sigma C_J\ne 0,\end{align*} $$
it is not difficult to see that
 $$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(y\xi))= \sum b_{\sigma,x} n({\omega_y(x)})^{\dot{s}}\sigma C_J,\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(y\xi))= \sum b_{\sigma,x} n({\omega_y(x)})^{\dot{s}}\sigma C_J,\end{align*} $$
which is also nonzero. Therefore,
 $$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s}y \xi)= \mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(y\xi))\ne 0.\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{\sigma}(\dot{s}y \xi)= \mathfrak{P}_{\sigma}(\dot{s} \cdot \sum_{v\in \spadesuit}\mathfrak{P}_v(y\xi))\ne 0.\end{align*} $$
By the argument above, we can do induction on the length of h and thus the lemma is proved.
The nonvanishing property of the augmentation
![]() $\epsilon $
on
$\epsilon $
on
![]() $E_J$
is as follows:
$E_J$
is as follows:
Proposition 4.2. Let
![]() $\xi \in E_J $
be a nonzero element. Then there exists
$\xi \in E_J $
be a nonzero element. Then there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $\epsilon (g\xi )$
is nonzero.
$\epsilon (g\xi )$
is nonzero.
Proof. By Lemma 4.1, we can assume that
![]() $\mathfrak {P}_e(\xi )$
is nonzero. For
$\mathfrak {P}_e(\xi )$
is nonzero. For
 $$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in E_J,\end{align*} $$
$$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in E_J,\end{align*} $$
we say that
![]() $\xi $
satisfies the condition
$\xi $
satisfies the condition
![]() $\heartsuit _h$
if
$\heartsuit _h$
if
 $\displaystyle \sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
for some
$\displaystyle \sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
for some
![]() $h\in W_J$
. We prove the following claim: if
$h\in W_J$
. We prove the following claim: if
![]() $\xi $
satisfies the condition
$\xi $
satisfies the condition
![]() $\heartsuit _h$
for some
$\heartsuit _h$
for some
![]() $h\in W_J$
, then there exists
$h\in W_J$
, then there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero.
$\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero.
We prove this claim by induction on the length of h. If
![]() $h=e$
, then it is obvious that
$h=e$
, then it is obvious that
 $\epsilon _e \mathfrak {P}_e(\xi )= \displaystyle \sum _{x\in {\mathbf U}_{w_J}} a_{e,x}$
which is already nonzero. We assume that the claim is valid for any
$\epsilon _e \mathfrak {P}_e(\xi )= \displaystyle \sum _{x\in {\mathbf U}_{w_J}} a_{e,x}$
which is already nonzero. We assume that the claim is valid for any
![]() $h\in W_J$
with
$h\in W_J$
with
![]() $\ell (h)\leq m$
. Now let
$\ell (h)\leq m$
. Now let
![]() $h\in W_J$
with
$h\in W_J$
with
![]() $\ell (h)=m+1$
such that
$\ell (h)=m+1$
such that
 $\displaystyle \sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
. We have
$\displaystyle \sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
. We have
![]() $h=\tau s$
for some
$h=\tau s$
for some
![]() $s\in \mathscr {R}(h)$
. Then
$s\in \mathscr {R}(h)$
. Then
![]() ${\mathbf U}_h= {\mathbf U}^s_\tau \cdot {\mathbf U}_s$
and
${\mathbf U}_h= {\mathbf U}^s_\tau \cdot {\mathbf U}_s$
and
![]() ${\mathbf U}^{\prime }_{\tau }=({\mathbf U^{\prime }_{\kern-1.5pt h}})^s \cdot {\mathbf U}_s$
by definition. Now our aim is to show that there exists
${\mathbf U}^{\prime }_{\tau }=({\mathbf U^{\prime }_{\kern-1.5pt h}})^s \cdot {\mathbf U}_s$
by definition. Now our aim is to show that there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $g\xi $
satisfies the condition
$g\xi $
satisfies the condition
![]() $\heartsuit _\tau $
.
$\heartsuit _\tau $
.
First, we prove that the element
![]() $\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
$\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
![]() $\heartsuit _\tau $
. Since
$\heartsuit _\tau $
. Since
![]() ${\mathbf U}_{w_J}= {\mathbf U}^{\prime }_h{\mathbf U}_h= {\mathbf U}^{\prime }_h{\mathbf U}^s_\tau {\mathbf U}_s $
, each element
${\mathbf U}_{w_J}= {\mathbf U}^{\prime }_h{\mathbf U}_h= {\mathbf U}^{\prime }_h{\mathbf U}^s_\tau {\mathbf U}_s $
, each element
![]() $x\in {\mathbf U}_{w_J}$
has a unique expression
$x\in {\mathbf U}_{w_J}$
has a unique expression
We just need to consider the coefficients of
![]() $a_{e, x}$
with
$a_{e, x}$
with
![]() $\dot {s} x^{\prime }_h x_{\tau } \dot {s}^{-1} \in {\mathbf U}^{\prime }_{\tau }$
, which implies that
$\dot {s} x^{\prime }_h x_{\tau } \dot {s}^{-1} \in {\mathbf U}^{\prime }_{\tau }$
, which implies that
![]() $x_{\tau }=id$
. For the case
$x_{\tau }=id$
. For the case
![]() $x_s\ne id$
, using Lemma 2.2 (c), we have
$x_s\ne id$
, using Lemma 2.2 (c), we have
where
![]() $x^{\prime \prime }_h= \dot {s} x^{\prime }_h \dot {s}^{-1} \in ({\mathbf U^{\prime }_h})^s \subset {\mathbf U}^{\prime }_{\tau }$
and
$x^{\prime \prime }_h= \dot {s} x^{\prime }_h \dot {s}^{-1} \in ({\mathbf U^{\prime }_h})^s \subset {\mathbf U}^{\prime }_{\tau }$
and
![]() $f(x_s)\in {\mathbf U}_s$
. Therefore if we write
$f(x_s)\in {\mathbf U}_s$
. Therefore if we write
 $$ \begin{align*}\dot{s} \cdot \mathfrak{P}_e(\xi)= \sum_{x\in {\mathbf U}_{w_J}}b_{e,x} x C_J,\end{align*} $$
$$ \begin{align*}\dot{s} \cdot \mathfrak{P}_e(\xi)= \sum_{x\in {\mathbf U}_{w_J}}b_{e,x} x C_J,\end{align*} $$
then
 $\displaystyle \sum _{x\in {\mathbf U}^{\prime }_\tau } b_{e,x} = -\sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
. Thus
$\displaystyle \sum _{x\in {\mathbf U}^{\prime }_\tau } b_{e,x} = -\sum _{x\in {\mathbf U}^{\prime }_h} a_{e,x}\ne 0$
. Thus
![]() $\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
$\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
![]() $\heartsuit _\tau $
.
$\heartsuit _\tau $
.
Now we consider
![]() $\dot {s}\xi $
and if
$\dot {s}\xi $
and if
![]() $\dot {s}\xi $
satisfies the condition
$\dot {s}\xi $
satisfies the condition
![]() $\heartsuit _\tau $
, we are done. Otherwise, there exists at least one element
$\heartsuit _\tau $
, we are done. Otherwise, there exists at least one element
![]() $v\in Y_J$
which satisfies the following condition
$v\in Y_J$
which satisfies the following condition
The subset of
![]() $Y_J$
whose elements satisfy this condition is also denoted by
$Y_J$
whose elements satisfy this condition is also denoted by
![]() $\clubsuit $
. With this setting,
$\clubsuit $
. With this setting,
 $\displaystyle \dot {s} \cdot \mathfrak {P}_e(\xi )+ \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
does not satisfy the condition
$\displaystyle \dot {s} \cdot \mathfrak {P}_e(\xi )+ \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
does not satisfy the condition
![]() $\heartsuit _\tau $
, which implies that
$\heartsuit _\tau $
, which implies that
 $\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
satisfies the condition
$\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
satisfies the condition
![]() $\heartsuit _\tau $
since we have proved that
$\heartsuit _\tau $
since we have proved that
![]() $\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
$\dot {s} \cdot \mathfrak {P}_e(\xi )$
satisfies the condition
![]() $\heartsuit _\tau $
. Since
$\heartsuit _\tau $
. Since
![]() ${\mathbf U}$
is infinite, we can choose an element
${\mathbf U}$
is infinite, we can choose an element
![]() $y\in {\mathbf U}_s$
such that the
$y\in {\mathbf U}_s$
such that the
![]() $ {\mathbf U}_s$
-component of
$ {\mathbf U}_s$
-component of
![]() $yx$
is nontrivial for any x with
$yx$
is nontrivial for any x with
![]() $a_{e, x} \ne 0$
. Then we consider the element
$a_{e, x} \ne 0$
. Then we consider the element
![]() $\dot {s}y\xi $
. Using Lemma 2.2 (c), it is easy to see that
$\dot {s}y\xi $
. Using Lemma 2.2 (c), it is easy to see that
![]() $\dot {s}\cdot \mathfrak {P}_e(y\xi )$
does not satisfy the condition
$\dot {s}\cdot \mathfrak {P}_e(y\xi )$
does not satisfy the condition
![]() $\heartsuit _\tau $
.
$\heartsuit _\tau $
.
Now for
![]() $v\in \clubsuit $
and
$v\in \clubsuit $
and
![]() $x\in {\mathbf U}_{w_Jv^{-1}}$
with
$x\in {\mathbf U}_{w_Jv^{-1}}$
with
![]() $a_{v,x}\ne 0$
, noting that the
$a_{v,x}\ne 0$
, noting that the
![]() ${\mathbf U}_s$
-component of x is trivial, we write
${\mathbf U}_s$
-component of x is trivial, we write
For
![]() $y\in {\mathbf U}_s$
, using the commutator relations of root subgroups, we have
$y\in {\mathbf U}_s$
, using the commutator relations of root subgroups, we have
and
Since
![]() ${\mathbf U}^{\prime }_{\tau }= ({\mathbf U}^{\prime }_h)^s {\mathbf U}_s$
, we get
${\mathbf U}^{\prime }_{\tau }= ({\mathbf U}^{\prime }_h)^s {\mathbf U}_s$
, we get
![]() $m(x)^{\dot {s}}\in {\mathbf U}^{\prime }_{\tau }$
if and only if
$m(x)^{\dot {s}}\in {\mathbf U}^{\prime }_{\tau }$
if and only if
![]() $m(x)\in ({\mathbf U}^{\prime }_h)^s $
. Thus,
$m(x)\in ({\mathbf U}^{\prime }_h)^s $
. Thus,
![]() $m_y(x)^{\dot {s}} \in {\mathbf U}^{\prime }_{\tau }$
if and only if
$m_y(x)^{\dot {s}} \in {\mathbf U}^{\prime }_{\tau }$
if and only if
![]() $m(x)^{\dot {s}} \in {\mathbf U}^{\prime }_{\tau }$
. Therefore, if we write
$m(x)^{\dot {s}} \in {\mathbf U}^{\prime }_{\tau }$
. Therefore, if we write
 $$ \begin{align*}\mathfrak{P}_{e}(\dot{s} \cdot \sum_{v\in\clubsuit}\mathfrak{P}_v(\xi))=\sum b_{x} m(x)^{\dot{s}} C_J,\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{e}(\dot{s} \cdot \sum_{v\in\clubsuit}\mathfrak{P}_v(\xi))=\sum b_{x} m(x)^{\dot{s}} C_J,\end{align*} $$
it is not difficult to see that
 $$ \begin{align*}\mathfrak{P}_{e}(\dot{s} \cdot \sum_{v\in \clubsuit}\mathfrak{P}_v(y\xi))=\sum b_{x} m_y(x)^{\dot{s}} C_J.\end{align*} $$
$$ \begin{align*}\mathfrak{P}_{e}(\dot{s} \cdot \sum_{v\in \clubsuit}\mathfrak{P}_v(y\xi))=\sum b_{x} m_y(x)^{\dot{s}} C_J.\end{align*} $$
Noting that
 $\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
satisfies the condition
$\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(\xi ))$
satisfies the condition
![]() $\heartsuit _\tau $
, we see that
$\heartsuit _\tau $
, we see that
 $\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(y\xi ))$
satisfies the condition
$\displaystyle \mathfrak {P}_{e}(\dot {s} \cdot \sum _{v\in \clubsuit }\mathfrak {P}_v(y\xi ))$
satisfies the condition
![]() $\heartsuit _\tau $
. Finally, there exists
$\heartsuit _\tau $
. Finally, there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $g\xi $
satisfies the condition
$g\xi $
satisfies the condition
![]() $\heartsuit _e$
, which implies that
$\heartsuit _e$
, which implies that
![]() $\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero. We have proved our claim.
$\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero. We have proved our claim.
Now we can assume that
![]() $a_{e,id}\ne 0$
. Thus, the element
$a_{e,id}\ne 0$
. Thus, the element
![]() $\xi $
satisfies the condition
$\xi $
satisfies the condition
![]() $\heartsuit _{w_J}$
. According to our claim, there exists
$\heartsuit _{w_J}$
. According to our claim, there exists
![]() $g\in {\mathbf G}$
such that
$g\in {\mathbf G}$
such that
![]() $\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero. In particular,
$\epsilon _e \mathfrak {P}_e(g\xi )$
is nonzero. In particular,
![]() $\epsilon (g\xi )$
is nonzero and the proposition is proved.
$\epsilon (g\xi )$
is nonzero and the proposition is proved.
5 Proof of the main theorem
In this section, we give the proof of Theorem 1.1. First, we deal with the cases: (1)
![]() $\text {char} \ \Bbbk =0$
and (2)
$\text {char} \ \Bbbk =0$
and (2)
![]() $\text {char} \ \Bbbk>0$
and
$\text {char} \ \Bbbk>0$
and
![]() $\text {char} \ \Bbbk \ne \text {char} \ \mathbb {F}$
. For
$\text {char} \ \Bbbk \ne \text {char} \ \mathbb {F}$
. For
![]() $J\subset I$
, we show that any nonzero submodule M of
$J\subset I$
, we show that any nonzero submodule M of
![]() $E_J$
contains
$E_J$
contains
![]() $C_J$
, and hence
$C_J$
, and hence
![]() $M=E_J$
. In particular,
$M=E_J$
. In particular,
![]() $E_J$
is irreducible for any
$E_J$
is irreducible for any
![]() $J\subset I$
. Let
$J\subset I$
. Let
![]() $\xi \in M$
be a nonzero element with the following expression
$\xi \in M$
be a nonzero element with the following expression
 $$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in M.\end{align*} $$
$$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in M.\end{align*} $$
By Proposition 4.2, we can assume that
![]() $\epsilon (\xi ) \ne 0$
. In the case (1) by [Reference Putman and Snowden6, Prop. 5.4] and in the case (2) by [Reference Putman and Snowden6, Prop. 6.7], we have
$\epsilon (\xi ) \ne 0$
. In the case (1) by [Reference Putman and Snowden6, Prop. 5.4] and in the case (2) by [Reference Putman and Snowden6, Prop. 6.7], we have
 $$ \begin{align*}\sum_{w\in Y_J}\sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} w C_J \in M.\end{align*} $$
$$ \begin{align*}\sum_{w\in Y_J}\sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} w C_J \in M.\end{align*} $$
In particular, we see that
 $$ \begin{align*}M\cap \sum_{w\in Y_J}\mathbb{F} w C_J\neq0.\end{align*} $$
$$ \begin{align*}M\cap \sum_{w\in Y_J}\mathbb{F} w C_J\neq0.\end{align*} $$
Noting that the discussion in the proof of [Reference Chen and Dong2, Claim 2] is still valid in our general setting, we see that
![]() $E_J$
is irreducible for any
$E_J$
is irreducible for any
![]() $J\subset I$
. The
$J\subset I$
. The
![]() $E_J$
’s are pairwise nonisomorphic by Proposition 2.5.
$E_J$
’s are pairwise nonisomorphic by Proposition 2.5.
It remains to consider the case
![]() $\text {char} \ \Bbbk = \text {char} \ \mathbb {F}=p>0$
. From now on, we assume that
$\text {char} \ \Bbbk = \text {char} \ \mathbb {F}=p>0$
. From now on, we assume that
![]() $\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p$
. For any finite subset X of
$\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p$
. For any finite subset X of
![]() ${\mathbf G}$
, let
${\mathbf G}$
, let
![]() $\underline {X}:=\sum _{x\in X}x \in \mathbb {F} {\mathbf G}$
. The following lemma is easy to get and will be very useful in our later discussion.
$\underline {X}:=\sum _{x\in X}x \in \mathbb {F} {\mathbf G}$
. The following lemma is easy to get and will be very useful in our later discussion.
Lemma 5.1. Let P be a finite abelian p-group such that
![]() $P=H\times K$
, where
$P=H\times K$
, where
![]() $H, K$
are two subgroups of P. Let
$H, K$
are two subgroups of P. Let
![]() $H'$
be a subgroup of P such that
$H'$
be a subgroup of P such that
![]() $|H'|=|H|$
. Then
$|H'|=|H|$
. Then
![]() $\underline {H'}\ \underline {K}= 0$
or
$\underline {H'}\ \underline {K}= 0$
or
![]() $\underline {P}$
.
$\underline {P}$
.
For a self-enclosed subgroup H of
![]() ${\mathbf U}$
, set
${\mathbf U}$
, set
![]() $H_{\gamma }=H \cap {\mathbf U}_{\gamma }$
as before for each
$H_{\gamma }=H \cap {\mathbf U}_{\gamma }$
as before for each
![]() $\gamma \in \Phi ^+$
. Let
$\gamma \in \Phi ^+$
. Let
![]() $\Phi ^+= \{\delta _1, \delta _2, \dots , \delta _m\}$
. We have
$\Phi ^+= \{\delta _1, \delta _2, \dots , \delta _m\}$
. We have
Let
![]() $H_w= H\cap {\mathbf U}_w$
. Then we have
$H_w= H\cap {\mathbf U}_w$
. Then we have
 $\displaystyle H_w= \prod _{\gamma \in \Phi ^{-}_w} H_{\gamma }$
and
$\displaystyle H_w= \prod _{\gamma \in \Phi ^{-}_w} H_{\gamma }$
and
 $\displaystyle \underline {H_w}= \prod _{\gamma \in \Phi ^{-}_w} \underline {H_{\gamma }}.$
The following two lemmas are very crucial in the later proof of Theorem 1.1.
$\displaystyle \underline {H_w}= \prod _{\gamma \in \Phi ^{-}_w} \underline {H_{\gamma }}.$
The following two lemmas are very crucial in the later proof of Theorem 1.1.
Lemma 5.2. Assume that
![]() $\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
and let M be a nonzero
$\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
and let M be a nonzero
![]() $\mathbb {F}{\mathbf G}$
-submodule of
$\mathbb {F}{\mathbf G}$
-submodule of
![]() $E_J$
. Then there exist an element
$E_J$
. Then there exist an element
![]() $w\in Y_J$
and a finite p-subgroup X of
$w\in Y_J$
and a finite p-subgroup X of
![]() ${\mathbf U}_{w_Jw^{-1}}$
such that
${\mathbf U}_{w_Jw^{-1}}$
such that
![]() $\underline {X} wC_J \in M$
.
$\underline {X} wC_J \in M$
.
Proof. Let
![]() $\xi $
be a nonzero element of M which has the form
$\xi $
be a nonzero element of M which has the form
 $$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in E_J.\end{align*} $$
$$ \begin{align*}\xi= \sum_{w\in Y_J} \sum_{x\in {\mathbf U}_{w_Jw^{-1}}}a_{w,x} x w C_J \in E_J.\end{align*} $$
By Lemma 3.3, there exists a self-enclosed finite p-subgroup V of
![]() ${\mathbf U}$
, which contains all
${\mathbf U}$
, which contains all
![]() $x\in {\mathbf U}_{w_Jw^{-1}}$
with
$x\in {\mathbf U}_{w_Jw^{-1}}$
with
![]() $a_{w,x}\ne 0$
. Then we have
$a_{w,x}\ne 0$
. Then we have
 $$ \begin{align*}\mathbb{F} V \xi\subset \bigoplus_{w\in Y_J} \mathbb{F} V_{w_Jw^{-1}} w C_J,\end{align*} $$
$$ \begin{align*}\mathbb{F} V \xi\subset \bigoplus_{w\in Y_J} \mathbb{F} V_{w_Jw^{-1}} w C_J,\end{align*} $$
as
![]() $\mathbb {F} V$
-modules. Since
$\mathbb {F} V$
-modules. Since
![]() $(\mathbb {F} V \xi )^{V}\ne 0$
by [Reference Serre7, Prop. 26] and noting that
$(\mathbb {F} V \xi )^{V}\ne 0$
by [Reference Serre7, Prop. 26] and noting that
 $$ \begin{align*}(\bigoplus_{w\in Y_J} \mathbb{F} V_{w_Jw^{-1}} w C_J)^{V}\subset \bigoplus_{w\in Y_J}\mathbb{F} \underline{V_{w_Jw^{-1}}} w C_J,\end{align*} $$
$$ \begin{align*}(\bigoplus_{w\in Y_J} \mathbb{F} V_{w_Jw^{-1}} w C_J)^{V}\subset \bigoplus_{w\in Y_J}\mathbb{F} \underline{V_{w_Jw^{-1}}} w C_J,\end{align*} $$
there exists a nonzero element
 $$ \begin{align*}\eta= \sum_{w\in Y_J} a_w \underline{V_{w_Jw^{-1}}} w C_J\in \mathbb{F} V \xi \subset M.\end{align*} $$
$$ \begin{align*}\eta= \sum_{w\in Y_J} a_w \underline{V_{w_Jw^{-1}}} w C_J\in \mathbb{F} V \xi \subset M.\end{align*} $$
Set
![]() $A(\eta )=\{w\in Y_J\mid a_w\ne 0\}$
. If
$A(\eta )=\{w\in Y_J\mid a_w\ne 0\}$
. If
![]() $|A(\eta )|=1$
, the lemma is proved.
$|A(\eta )|=1$
, the lemma is proved.
Now we assume that
![]() $|A(\eta )|\geq 2$
. We set
$|A(\eta )|\geq 2$
. We set
 $\Phi (\eta )=\displaystyle \bigcup _{w\in A(\eta ) } \Phi _{w_Jw^{-1}}^- $
. Let
$\Phi (\eta )=\displaystyle \bigcup _{w\in A(\eta ) } \Phi _{w_Jw^{-1}}^- $
. Let
![]() $\Phi (\eta )=\{\gamma _1, \gamma _2, \dots , \gamma _d\}$
such that
$\Phi (\eta )=\{\gamma _1, \gamma _2, \dots , \gamma _d\}$
such that
![]() $\text {ht}(\gamma _1)\leq \text {ht}(\gamma _2) \leq \dots \leq \text {ht}(\gamma _d)$
. Let s be the maximal integer such that
$\text {ht}(\gamma _1)\leq \text {ht}(\gamma _2) \leq \dots \leq \text {ht}(\gamma _d)$
. Let s be the maximal integer such that
 $\gamma _s\notin \displaystyle \bigcap _{w\in A(\eta ) } \Phi _{w_Jw^{-1}}^- $
. Let
$\gamma _s\notin \displaystyle \bigcap _{w\in A(\eta ) } \Phi _{w_Jw^{-1}}^- $
. Let
![]() $y\in {\mathbf U}_{\gamma _s}\backslash V_{\gamma _s}$
and H be a self-enclosed finite p-subgroup of
$y\in {\mathbf U}_{\gamma _s}\backslash V_{\gamma _s}$
and H be a self-enclosed finite p-subgroup of
![]() ${\mathbf U}_{\gamma _s}{\mathbf U}_{\gamma _{s+1}}\dots {\mathbf U}_{\gamma _d}$
such that H contains
${\mathbf U}_{\gamma _s}{\mathbf U}_{\gamma _{s+1}}\dots {\mathbf U}_{\gamma _d}$
such that H contains
![]() $V_{\gamma _s}V_{\gamma _{s+1}}\dots V_{\gamma _d}$
and y. Let X be the self-enclosed subgroup of
$V_{\gamma _s}V_{\gamma _{s+1}}\dots V_{\gamma _d}$
and y. Let X be the self-enclosed subgroup of
![]() $\mathbf U$
which is generated by H and V. Then it is easy to see that X has the following form
$\mathbf U$
which is generated by H and V. Then it is easy to see that X has the following form
where
![]() $X_{\gamma _k}= X\cap {\mathbf U}_{\gamma _k}$
for
$X_{\gamma _k}= X\cap {\mathbf U}_{\gamma _k}$
for
![]() $s\leq k\leq d$
. Denote by
$s\leq k\leq d$
. Denote by
![]() $\Omega _s$
a set of the left coset representatives of
$\Omega _s$
a set of the left coset representatives of
![]() $V_{\gamma _s}V_{\gamma _{s+1}}\dots V_{\gamma _d}$
in
$V_{\gamma _s}V_{\gamma _{s+1}}\dots V_{\gamma _d}$
in
![]() $X_{\gamma _s} X_{\gamma _{s+1}} \dots X_{\gamma _d}$
. For the
$X_{\gamma _s} X_{\gamma _{s+1}} \dots X_{\gamma _d}$
. For the
![]() $w\in Y_J$
such that
$w\in Y_J$
such that
![]() $\gamma _s \in \Phi _{w_Jw^{-1}}^- $
, we have
$\gamma _s \in \Phi _{w_Jw^{-1}}^- $
, we have
For the
![]() $w\in Y_J$
such that
$w\in Y_J$
such that
![]() $\gamma _s \notin \Phi _{w_Jw^{-1}}^- $
, we have
$\gamma _s \notin \Phi _{w_Jw^{-1}}^- $
, we have
![]() $\underline {\Omega _s} \ \underline {V_{w_Jw^{-1}}} w C_J= 0$
since
$\underline {\Omega _s} \ \underline {V_{w_Jw^{-1}}} w C_J= 0$
since
![]() $\text {char}\ \mathbb {F} =p$
. Then we get
$\text {char}\ \mathbb {F} =p$
. Then we get
 $$ \begin{align*}\eta'= \underline{\Omega_s} \ \eta= \sum_{w\in Y_J} b_w \underline{X_{w_Jw^{-1}}} w C_J,\end{align*} $$
$$ \begin{align*}\eta'= \underline{\Omega_s} \ \eta= \sum_{w\in Y_J} b_w \underline{X_{w_Jw^{-1}}} w C_J,\end{align*} $$
which satisfies that
![]() $|A(\eta ')| < |A(\eta )|$
, where
$|A(\eta ')| < |A(\eta )|$
, where
![]() $A(\eta ')=\{w\in Y_J\mid b_w\ne 0\} $
. Thus by the induction on the cardinality of
$A(\eta ')=\{w\in Y_J\mid b_w\ne 0\} $
. Thus by the induction on the cardinality of
![]() $A(\eta )$
, the lemma is proved.
$A(\eta )$
, the lemma is proved.
Lemma 5.3. Assume that
![]() $\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
and let M be a nonzero
$\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
and let M be a nonzero
![]() $\mathbb {F} {\mathbf G}$
-submodule of
$\mathbb {F} {\mathbf G}$
-submodule of
![]() $E_J$
. If there exists a finite p-subgroup X of
$E_J$
. If there exists a finite p-subgroup X of
![]() ${\mathbf U}_{w_Jw^{-1}s}$
such that
${\mathbf U}_{w_Jw^{-1}s}$
such that
![]() $\underline {X} swC_J \in M$
, where
$\underline {X} swC_J \in M$
, where
![]() $sw\in Y_J$
and
$sw\in Y_J$
and
![]() $sw>w$
(which implies that
$sw>w$
(which implies that
![]() $w\in Y_J$
), then there exists a finite p-subgroup H of
$w\in Y_J$
), then there exists a finite p-subgroup H of
![]() ${\mathbf U}_{w_Jw^{-1}}$
such that
${\mathbf U}_{w_Jw^{-1}}$
such that
![]() $\underline {H} wC_J \in M$
.
$\underline {H} wC_J \in M$
.
Proof. Using Lemma 3.3, we can assume that X is a self-enclosed subgroup of
![]() ${\mathbf U}_{w_Jw^{-1}s}$
. Since
${\mathbf U}_{w_Jw^{-1}s}$
. Since
![]() ${\mathbf U}_{w_Jw^{-1}s}= {\mathbf U}_{s} ({\mathbf U}_{w_Jw^{-1}})^s $
, we can write
${\mathbf U}_{w_Jw^{-1}s}= {\mathbf U}_{s} ({\mathbf U}_{w_Jw^{-1}})^s $
, we can write
![]() $X= X_{\alpha } V $
, where
$X= X_{\alpha } V $
, where
![]() $V= X\cap ({\mathbf U}_{w_Jw^{-1}})^s$
is also a self-enclosed subgroup of
$V= X\cap ({\mathbf U}_{w_Jw^{-1}})^s$
is also a self-enclosed subgroup of
![]() $({\mathbf U}_{w_Jw^{-1}})^s$
. Thus, we have
$({\mathbf U}_{w_Jw^{-1}})^s$
. Thus, we have
![]() $\underline {X}= \underline {X_{\alpha }}\ \underline {V}$
. In the following, we will prove that if
$\underline {X}= \underline {X_{\alpha }}\ \underline {V}$
. In the following, we will prove that if
![]() $\underline {Y}\ \underline {V} \ swC_J \in M$
for some finite subset Y of
$\underline {Y}\ \underline {V} \ swC_J \in M$
for some finite subset Y of
![]() $ {\mathbf U}_{s}$
and a self-enclosed subgroup V of
$ {\mathbf U}_{s}$
and a self-enclosed subgroup V of
![]() $({\mathbf U}_{w_Jw^{-1}})^s$
, then there exists a finite p-subgroup H of
$({\mathbf U}_{w_Jw^{-1}})^s$
, then there exists a finite p-subgroup H of
![]() ${\mathbf U}_{w_Jw^{-1}}$
such that
${\mathbf U}_{w_Jw^{-1}}$
such that
![]() $\underline {H} wC_J \in M$
. Without loss of generality, we can assume that Y contains the neutral element of
$\underline {H} wC_J \in M$
. Without loss of generality, we can assume that Y contains the neutral element of
![]() ${\mathbf U}_s$
.
${\mathbf U}_s$
.
For each
![]() $u\in {\mathbf U}_{\alpha }\backslash \{id\}$
, we have
$u\in {\mathbf U}_{\alpha }\backslash \{id\}$
, we have
where
![]() $f_\alpha (u), g_\alpha (u) \in {\mathbf U}_{\alpha }$
and
$f_\alpha (u), g_\alpha (u) \in {\mathbf U}_{\alpha }$
and
![]() $ h_{\alpha }(u)\in {\mathbf T}$
are uniquely determined. Then
$ h_{\alpha }(u)\in {\mathbf T}$
are uniquely determined. Then
Without loss of generality, we can assume that the group V contains enough elements such that
for any
![]() $u\in Y\backslash \{id\}$
. Indeed, we let
$u\in Y\backslash \{id\}$
. Indeed, we let
and H be a self-enclosed subgroup which contains
![]() $G_{\alpha }(X)$
and
$G_{\alpha }(X)$
and
![]() $\dot {s}^{-1}V \dot {s}$
. Then
$\dot {s}^{-1}V \dot {s}$
. Then
![]() $H_{w_Jw^{-1}}= H \cap {\mathbf U}_{w_Jw^{-1}}$
is also a self-enclosed subgroup which contains
$H_{w_Jw^{-1}}= H \cap {\mathbf U}_{w_Jw^{-1}}$
is also a self-enclosed subgroup which contains
![]() $\dot {s}^{-1}V \dot {s}$
. Then we can consider
$\dot {s}^{-1}V \dot {s}$
. Then we can consider
![]() $ \underline {Y}\ \underline {\dot {s}H_{w_Jw^{-1}}\dot {s}^{-1}}$
instead of
$ \underline {Y}\ \underline {\dot {s}H_{w_Jw^{-1}}\dot {s}^{-1}}$
instead of
![]() $\underline {Y}\ \underline {V}$
from the beginning. Noting that
$\underline {Y}\ \underline {V}$
from the beginning. Noting that
![]() $h_{\alpha }(u) \in {\mathbf T}$
, we have
$h_{\alpha }(u) \in {\mathbf T}$
, we have
which implies that
 $$ \begin{align*}\dot{s}\underline{Y}\ \underline{V} swC_J = \underline{\dot{s}V \dot{s}^{-1}} wC_J+ \sum_{u\in Y\backslash\{id\} }f_\alpha(u)\underline{ {h_{\alpha}(u)Vh_{\alpha}(u)}^{-1}} swC_J.\end{align*} $$
$$ \begin{align*}\dot{s}\underline{Y}\ \underline{V} swC_J = \underline{\dot{s}V \dot{s}^{-1}} wC_J+ \sum_{u\in Y\backslash\{id\} }f_\alpha(u)\underline{ {h_{\alpha}(u)Vh_{\alpha}(u)}^{-1}} swC_J.\end{align*} $$
Now we let
such that
![]() $\text {ht}(\beta _1) \leq \text {ht}(\beta _2)\leq \dots \leq \text {ht}(\beta _m)$
. Since
$\text {ht}(\beta _1) \leq \text {ht}(\beta _2)\leq \dots \leq \text {ht}(\beta _m)$
. Since
![]() $sw\in Y_J$
and
$sw\in Y_J$
and
![]() $sw>w$
, we have
$sw>w$
, we have
![]() $ ({\mathbf U}_{w_Jw^{-1}})^s \ne {\mathbf U}_{w_Jw^{-1}}$
by [Reference Chen and Dong3, Cor. 2.2]. Now let r be the maximal integer such that
$ ({\mathbf U}_{w_Jw^{-1}})^s \ne {\mathbf U}_{w_Jw^{-1}}$
by [Reference Chen and Dong3, Cor. 2.2]. Now let r be the maximal integer such that
![]() $\beta _r\notin \Phi ^-_{w_Jw^{-1}} \cap \Phi ^-_{w_Jw^{-1}s} $
and
$\beta _r\notin \Phi ^-_{w_Jw^{-1}} \cap \Phi ^-_{w_Jw^{-1}s} $
and
![]() $\beta _j\in \Phi ^-_{w_Jw^{-1}} \cap \Phi ^-_{w_Jw^{-1}s} $
for
$\beta _j\in \Phi ^-_{w_Jw^{-1}} \cap \Phi ^-_{w_Jw^{-1}s} $
for
![]() $j>r$
. When
$j>r$
. When
![]() $\beta _r \in \Phi ^-_{w_Jw^{-1}} \backslash \Phi ^-_{w_Jw^{-1}s}$
, using Lemma 3.3, Lemma 5.1 and [Reference Chen and Dong3, Lem. 4.5], we can choose certain subgroup
$\beta _r \in \Phi ^-_{w_Jw^{-1}} \backslash \Phi ^-_{w_Jw^{-1}s}$
, using Lemma 3.3, Lemma 5.1 and [Reference Chen and Dong3, Lem. 4.5], we can choose certain subgroup
![]() $\Omega _k$
of
$\Omega _k$
of
![]() ${\mathbf U}_{\beta _k}$
for each
${\mathbf U}_{\beta _k}$
for each
![]() $r\leq k \leq m$
such that
$r\leq k \leq m$
such that
for any
![]() $u\in Y\backslash \{id\}$
and
$u\in Y\backslash \{id\}$
and
for some finite subgroup
![]() $\Omega $
of
$\Omega $
of
![]() ${\mathbf U}_{w_Jw^{-1}}$
. Then the lemma is proved in this case.
${\mathbf U}_{w_Jw^{-1}}$
. Then the lemma is proved in this case.
When
![]() $\beta _r \in \Phi ^-_{w_Jw^{-1}s} \backslash \Phi ^-_{w_Jw^{-1}}$
, also by Lemmas 3.3, 5.1 and [Reference Chen and Dong3, Lem. 4.5], we can choose certain subgroup
$\beta _r \in \Phi ^-_{w_Jw^{-1}s} \backslash \Phi ^-_{w_Jw^{-1}}$
, also by Lemmas 3.3, 5.1 and [Reference Chen and Dong3, Lem. 4.5], we can choose certain subgroup
![]() $\Gamma _k$
of
$\Gamma _k$
of
![]() ${\mathbf U}_{\beta _k}$
for each
${\mathbf U}_{\beta _k}$
for each
![]() $r\leq k \leq m$
such that there exists at least one
$r\leq k \leq m$
such that there exists at least one
![]() $u\in Y \backslash \{id\}$
which satisfies
$u\in Y \backslash \{id\}$
which satisfies
where
![]() $\Gamma $
is some finite subgroup of
$\Gamma $
is some finite subgroup of
![]() $({\mathbf U}_{w_Jw^{-1}})^s $
. On the other hand, these groups
$({\mathbf U}_{w_Jw^{-1}})^s $
. On the other hand, these groups
![]() $\Gamma _r, \Gamma _{r+1}, \dots , \Gamma _m$
also make
$\Gamma _r, \Gamma _{r+1}, \dots , \Gamma _m$
also make
Therefore, we get
 $\displaystyle \sum _{x\in F}x \underline {\Gamma } swC_J\in M$
for some set F with
$\displaystyle \sum _{x\in F}x \underline {\Gamma } swC_J\in M$
for some set F with
![]() $|F|< |Y|$
and some finite subgroup
$|F|< |Y|$
and some finite subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() $({\mathbf U}_{w_Jw^{-1}})^s $
. Hence by the same discussion as before, we get another element
$({\mathbf U}_{w_Jw^{-1}})^s $
. Hence by the same discussion as before, we get another element
 $\displaystyle \sum _{y\in F'} y \underline {\Gamma '} swC_J\in M$
for some set
$\displaystyle \sum _{y\in F'} y \underline {\Gamma '} swC_J\in M$
for some set
![]() $F'$
with
$F'$
with
![]() $|F'|< |F|$
and some finite subgroup
$|F'|< |F|$
and some finite subgroup
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $({\mathbf U}_{w_Jw^{-1}})^s $
. Finally, we get an element
$({\mathbf U}_{w_Jw^{-1}})^s $
. Finally, we get an element
![]() $\underline {K} swC_J\in M$
for some finite subgroup K of
$\underline {K} swC_J\in M$
for some finite subgroup K of
![]() $({\mathbf U}_{w_Jw^{-1}})^s $
. Thus, we have
$({\mathbf U}_{w_Jw^{-1}})^s $
. Thus, we have
![]() $\underline {K^{\dot {s}}} wC_J\in M$
and the lemma is proved.
$\underline {K^{\dot {s}}} wC_J\in M$
and the lemma is proved.
Finally, we prove the irreducibility of
![]() $E_J$
in the case
$E_J$
in the case
![]() $\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
using the previous lemmas. Let M be a nonzero
$\text {char} \ \mathbb {F}= \text {char} \ \Bbbk =p>0$
using the previous lemmas. Let M be a nonzero
![]() $\mathbb {F} {\mathbf G}$
-submodule of
$\mathbb {F} {\mathbf G}$
-submodule of
![]() $E_J$
. Combining Lemmas 5.2 and 5.3, there exists a finite p-subgroup H of
$E_J$
. Combining Lemmas 5.2 and 5.3, there exists a finite p-subgroup H of
![]() ${\mathbf U}_{w_J}$
such that
${\mathbf U}_{w_J}$
such that
![]() $\underline {H}C_J\in M$
. Similar to the arguments of [Reference Yang9, Lem. 2.5], we see that the sum of all coefficients of
$\underline {H}C_J\in M$
. Similar to the arguments of [Reference Yang9, Lem. 2.5], we see that the sum of all coefficients of
![]() $\dot {w_J}x C_J$
in terms the basis
$\dot {w_J}x C_J$
in terms the basis
![]() $\{uC_J\mid u\in {\mathbf U}_{w_J}\}$
is zero when x is not the neutral element of
$\{uC_J\mid u\in {\mathbf U}_{w_J}\}$
is zero when x is not the neutral element of
![]() ${\mathbf U}_{w_J}$
. So if we write
${\mathbf U}_{w_J}$
. So if we write
 $$ \begin{align*}\xi= w_J \underline{H}C_J= \displaystyle \sum_{x\in {\mathbf U}_{w_J} } a_x xC_J,\end{align*} $$
$$ \begin{align*}\xi= w_J \underline{H}C_J= \displaystyle \sum_{x\in {\mathbf U}_{w_J} } a_x xC_J,\end{align*} $$
we have
 $\displaystyle \sum _{x\in {\mathbf U}_{w_J} } a_x= (-1)^{\ell (w_J)}$
, which is nonzero. We consider the
$\displaystyle \sum _{x\in {\mathbf U}_{w_J} } a_x= (-1)^{\ell (w_J)}$
, which is nonzero. We consider the
![]() $\mathbb {F} {\mathbf U}_{w_J}$
-module generated by
$\mathbb {F} {\mathbf U}_{w_J}$
-module generated by
![]() $\xi $
, and then using [Reference Putman and Snowden6, Prop. 4.1], we see that
$\xi $
, and then using [Reference Putman and Snowden6, Prop. 4.1], we see that
![]() $C_J\in M$
. Therefore
$C_J\in M$
. Therefore
![]() $M=E_J$
, which implies the irreducibility of
$M=E_J$
, which implies the irreducibility of
![]() $E_J$
for any
$E_J$
for any
![]() $J\subset I$
. All the
$J\subset I$
. All the
![]() $\mathbb {F}{\mathbf G}$
-modules
$\mathbb {F}{\mathbf G}$
-modules
![]() $E_J$
are pairwise non-isomorphic by Proposition 2.5 and thus Theorem 1.1 is proved.
$E_J$
are pairwise non-isomorphic by Proposition 2.5 and thus Theorem 1.1 is proved.
Acknowledgement
The author is grateful to Nanhua Xi and Xiaoyu Chen for their suggestions and helpful discussions. The author also thanks the referee for the helpful comments which greatly improve the manuscript. The work is sponsored by Shanghai Sailing Program (No. 21YF1429000) and NSFC-12101405.