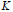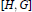Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vermani, L. R.
1999.
Algebra.
p.
227.
Vermani, L. R.
1999.
Algebra.
p.
227.
Karan, Ram
and
Kumar, Deepak
2002.
Some intersections and identifications in integral group rings.
Proceedings Mathematical Sciences,
Vol. 112,
Issue. 2,
p.
289.
Karan, Ram
and
Kumar, Deepak
2005.
Augmentation Quotients of Free Group Rings.
Algebra Colloquium,
Vol. 12,
Issue. 04,
p.
597.
HARTL, MANFRED
2010.
ON FOX QUOTIENTS OF ARBITRARY GROUP ALGEBRAS.
International Journal of Algebra and Computation,
Vol. 20,
Issue. 05,
p.
619.
Vermani, L. R.
2014.
On Certain Quotients of Lower Central Factors of a Normal Subgroup of a Free Group.
Communications in Algebra,
Vol. 42,
Issue. 8,
p.
3259.