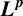 $\boldsymbol {L}^{\boldsymbol {p}}$–
$\boldsymbol {L}^{\boldsymbol {p}}$–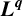 $\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
$\boldsymbol {L}^{\boldsymbol {q}}$ MULTIPLIERS ON COMMUTATIVE HYPERGROUPS
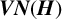 $\boldsymbol {VN(H)}$ AND
$\boldsymbol {VN(H)}$ AND 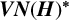 $\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP
$\boldsymbol {VN(H)^{*}} $ OF AN ULTRASPHERICAL HYPERGROUP 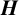 $\boldsymbol {H}$
$\boldsymbol {H}$