Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-24T18:37:30.155Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant Means on a Class of von Neumann Algebras Related to Ultraspherical Hypergroups II

Published online by Cambridge University Press:  20 November 2018

N. Shravan Kumar
N. Shravan Kumar*
Affiliation:
Department of Mathematics, Indian Institute of Technology Delhi, Delhi-110016, India. e-mail: shravankumar@maths.iitd.ac.in
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 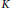$K$ be an ultraspherical hypergroup associated with a locally compact group $G$ and a spherical projector $\pi$ and let 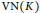$\text{VN}(K)$ denote the dual of the Fourier algebra 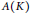$A(K)$ corresponding to 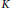$K$. In this note, we show that the set of invariant means on 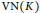$\text{VN}(K)$ is singleton if and only if 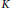$K$ is discrete. Here 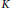$K$ need not be second countable. We also study invariant means on the dual of the Fourier algebra 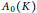${{A}_{0}}(K)$, the closure of 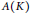$A(K)$ in the cb-multiplier norm. Finally, we consider generalized translations and generalized invariant means.

Keywords

43A6246J1043A3020N20ultraspherical hypergroupFourier algebraFourier-Stieltjes algebrainvariant meangeneralized translationgeneralized invariant mean
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 2 , 01 June 2017 , pp. 402 - 410
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Cheng, M. Y.-H., Dual spaces and translation invariant means on group von Neumann algebras. StudiaMath. 223(2014), 97–121. http://dx.doi.org/10.4064/sm223-2-1 Google Scholar
[2] Chu, C.-H. and Lau, A. T., Jordan structures in harmonic functions and Fourier algebras on homogeneous spaces. Math. Ann. 336(2006), 803–840. http://dx.doi.org/10.1007/s00208-006-0013-y Google Scholar
[3] Degenfeld-Schonburg, S., Kaniuth, E., and Lasser, R., Spectral synthesis in Fourier algebras of ultraspherical hypergroups. J. Fourier Anal. Appl. 20(2014), 258–281. http://dx.doi.org/10.1007/s00041-013-9311 -4 Google Scholar
[4] Effros, E. G. and Ruan, Z-J., Operator spaces. Oxford University Press, 2000.Google Scholar
[5] Folland, G. B., A course in abstract harmonic analysis. CRC Press, Boca Raton, FL, 1995. Google Scholar
[6] Forrest, B. E., Some Banach algebras without discontinuous derivations. Proc. Amer. Math. Soc. 114(1992), 965–970. http://dx.doi.org/10.1090/S0002-9939-1992-1068120-4 Google Scholar
[7] Forrest, B. E., Fourier analysis on coset spaces. Rocky Mountain J. Math. 28(1998), 173–190. http://dx.doi.org/10.1216/rmjm/1181071828 Google Scholar
[8] Forrest, B. E., Completely bounded multipliers and ideals in A(G) vanishing on closed subgroups. In: Banach algebras and their applications. Contemporary Mathematics, 363. American Mathematical Society, Providence, RI, 2004, pp-89-94. http://dx.doi.org/10.1090/conm/3 63/06644 Google Scholar
[9] Forrest, B. E. and Miao, T., Uniformly continuous functionals and M-weakly amenable groups. Canad. J. Math. 65(2013), 1005–1019. http://dx.doi.org/10.41 53/CJM-2O13-01 9-x Google Scholar
[10] Hewitt, E. and Ross, K. A., Abstract harmonic analysis. Vol I: Structure of topological groups, integration theory, group representations. Grundlehren der Math.Wissenschaften, 115. Springer, 1963. Google Scholar
[11] Jewett, R. I., Spaces with an abstract convolution of measures. Adv. in Math. 18(1975), 1–101. http://dx.doi.org/10.101 6/0001-8708(75)90002-X Google Scholar
[12] Lau, A. T. and Losert, V., The C*-algebra generated by operators with compact support on a locally compact group. J. Funct. Anal. 112(1993), 1–30. http://dx.doi.org/10.1006/jfan.1993.1024 Google Scholar
[13] Litvinov, G. L., Hypergroups and hypergroup algebras. J. Soviet Math. 38(1987), 1734–1761. Google Scholar
[14] Muruganandam, V., Fourier algebra of a hypergroup . I. J. Aust. Math. Soc. 82(2007), 59–83. http://dx.doi.org/10.101 7/S144678870001 747X Google Scholar
[15] Muruganandam, V., Fourier algebra of a hypergroup. II. Spherical hypergroups. Math. Nach. 11(2008), 1950–1603. http://dx.doi.org/10.1002/mana.200510699 Google Scholar
[16] Renaud, P. F., Invariant means on a class of von Neumann algebras. Trans. Amer. Math. Soc. 170(1972)285-291. http://dx.doi.org/10.1090/S0002-9947-1972-0304553-0 Google Scholar
[17] Shravan Kumar, N., Invariant means on a class of von Neumann algebras related to ultraspherical hypergroups. Studia Math. 225(2014), 235–247. http://dx.doi.org/! 0.4064/sm225-3-4 Google Scholar