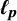 $\boldsymbol {\ell _{p}}$
structures for
$\boldsymbol {\ell _{p}}$
structures for
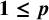 $ \boldsymbol {1\le p}$
<
$ \boldsymbol {1\le p}$
<
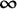 $ \boldsymbol {\infty }$
$ \boldsymbol {\infty }$
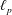 $\ell _{p}$ Spaces
$\ell _{p}$ Spaces
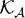 $\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
$\mathcal K_{\mathcal A}$-APPROXIMATION PROPERTY FOR BANACH SPACES
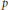 $p$-Convex,
$p$-Convex, 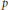 $p$-Concave and Positive
$p$-Concave and Positive 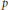 $p$-Summing Operators
$p$-Summing Operators