Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T04:27:28.980Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric sequence subspaces of C(α), II

Published online by Cambridge University Press:  20 November 2018

Denny H. Leung  and
Wee-Kee Tang
Denny H. Leung
Affiliation:
Department of Mathematics, National University of Singapore, Singapore 119260 email: matlhh@nus.edu.sg
Wee-Kee Tang
Affiliation:
National Institute of Education, Nanyang Technological University, 469 Bukit Timah Road, Singapore 259756 email: tangwk@nievax.nie.ac.sg
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 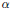$\alpha$ is an ordinal, then the space of all ordinals less than or equal to 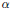$\alpha$ is a compact Hausdorff space when endowed with the order topology. Let 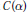$C(\alpha )$ be the space of all continuous real-valued functions defined on the ordinal interval 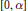$[0,\,\alpha ]$. We characterize the symmetric sequence spaces which embed into 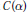$C(\alpha )$ for some countable ordinal 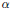$\alpha$. A hierarchy 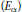$\left( {{E}_{\alpha }} \right)$ of symmetric sequence spaces is constructed so that, for each countable ordinal 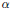$\alpha$, 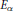${{E}_{\alpha }}$ embeds into 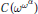$C\left( {{\omega }^{{{\omega }^{\alpha }}}} \right)$, but does not embed into 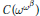$C\left( {{\omega }^{{{\omega }^{\beta }}}} \right)$ for any 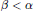$\beta \,<\,\alpha$.

Keywords

03E1303E1546B0346B4546E1554G12
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 2 , 01 April 1999 , pp. 309 - 325
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Alspach, D. and Argyros, S., Complexity of weakly null sequences. Dissertationes Math. (Rozprawy Mat.) 321 (1992), 1–44.Google Scholar
[2] Bessaga, C. and Pełczynski, A., Spaces of continuous functions (IV) (on isomorphical classification of spaces C(S)). Studia Math. 19 (1960), 53–62.Google Scholar
[3] Dugundji, James, Topology. Allyn and Bacon, Inc., Boston, 1966.Google Scholar
[4] Leung, Denny H., Symmetric sequence subspaces of C(α). J. LondonMath. Soc. (To appear.)Google Scholar
[5] Lindenstrauss, Joram and Tzafriri, Lior, Classical Banach Spaces I. Springer-Verlag, 1977.Google Scholar
[6] Mazurkiewicz, Stefan and Sierpiński, W., Contribution à la topologie des ensembles dénombrables. Fund.Math. 1 (1920), 17–27.Google Scholar
[7] Odell, E., Tomczak-Jaegermann, N., and Wagner, R., Proximity to `1 and Distortion in Asymptotic `1 spaces. J. Funct. Anal. 150 (1997), 101–145.Google Scholar
[8] Semadeni, Z., Banach Spaces of Continuous Functions. Polish Scientific Publishers, Warzawa, 1971.Google Scholar