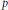Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bu∗, Qingying
Craddock, Michelle
and
Ji, Donghai
2009.
Reflexivity and the Grothendieck property for positive tensor products of Banach lattices-II.
Quaestiones Mathematicae,
Vol. 32,
Issue. 3,
p.
339.
Bu*, Qingying
Ji, Donghai
and
Li†, Yongjin
2011.
Copies ofℓ1in positive tensor products of Orlicz sequence spaces.
Quaestiones Mathematicae,
Vol. 34,
Issue. 4,
p.
407.
Achour, D.
and
Belacel, A.
2014.
Domination and factorization theorems for positive strongly $$p$$ p -summing operators.
Positivity,
Vol. 18,
Issue. 4,
p.
785.
Chen, Dongyang
Belacel, Amar
and
Chávez-Domínguez, Javier Alejandro
2021.
Positive p-summing operators and disjoint p-summing operators.
Positivity,
Vol. 25,
Issue. 3,
p.
1045.
Qingying, Bu
Rui, Liu
and
Jie, Shen
2023.
Positive multiple summing multilinear operators on bmL^p-spaces.
SCIENTIA SINICA Mathematica,
Belacel, Amar
Bougoutaia, Amar
and
Rueda, Pilar
2023.
Summability of multilinear operators and their linearizations on Banach lattices.
Journal of Mathematical Analysis and Applications,
Vol. 527,
Issue. 2,
p.
127459.