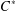 $C^{\ast }$-ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$-ENVELOPES OF EXACT OPERATOR SYSTEMS
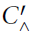 $C_{\hat{\ }}^{'}$, of Operator Spaces
$C_{\hat{\ }}^{'}$, of Operator Spaces
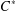 $C^{\ast }$ -ENVELOPES
$C^{\ast }$ -ENVELOPES
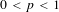 $0<p<1$
$0<p<1$
 ${\mathbb B}$(H) ⊗
${\mathbb B}$(H) ⊗  ${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS
${\mathbb B}$(H) AND RELATED TENSOR PRODUCTS