Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ricard, Éric
2018.
Fractional powers on noncommutative L for p < 1.
Advances in Mathematics,
Vol. 333,
Issue. ,
p.
194.
Cadilhac, Léonard
2019.
Noncommutative Khintchine inequalities in interpolation spaces of L-spaces.
Advances in Mathematics,
Vol. 352,
Issue. ,
p.
265.
Bakshi, Ainesh
Chepurko, Nadiia
and
Jayaram, Rajesh
2020.
Testing Positive Semi-Definiteness via Random Submatrices.
p.
1191.
Ricard, Éric
2021.
An $$L_p$$-Inequality for Anticommutators.
Integral Equations and Operator Theory,
Vol. 93,
Issue. 1,
Hong, Guixiang
and
Xu, Bang
2021.
A noncommutative weak type (1,1) estimate for a square function from ergodic theory.
Journal of Functional Analysis,
Vol. 280,
Issue. 9,
p.
108959.
Chuah, Chian Yeong
Han, Yazhou
Liu, Zhen-Chuan
and
Mei, Tao
2022.
Paley’s Inequality for Discrete Groups.
Journal of Fourier Analysis and Applications,
Vol. 28,
Issue. 5,
Huang, J.
Sukochev, F.
and
Zanin, D.
2022.
Operator θ$\theta$‐Hölder functions with respect to ∥·∥p$\Vert \cdot \Vert _p$, 0<p⩽∞$0< p\leqslant \infty$.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 4,
p.
2436.
Chen, Junxi
and
Cheng, Xiaoyu
2022.
A note on Poincaré constants.
Filomat,
Vol. 36,
Issue. 16,
p.
5463.
Chen, Zeqian
Randrianantoanina, Narcisse
and
Xu, Quanhua
2023.
Atomic decompositions for noncommutative martingales.
Journal of Functional Analysis,
Vol. 284,
Issue. 9,
p.
109877.
Spektor, Susanna
2024.
Non-commutative Khinchine-type inequality for dependent random variables and overview of its applications in data science.
Forum Mathematicum,
Vol. 36,
Issue. 1,
p.
5.
Chuah, Chian Yeong
Liu, Zhen-Chuan
and
Mei, Tao
2025.
A Marcinkiewicz multiplier theory for Schur multipliers.
Analysis & PDE,
Vol. 18,
Issue. 6,
p.
1511.
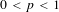 $0<p<1$
$0<p<1$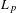 $L_{p}$-spaces for all
$L_{p}$-spaces for all 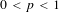 $0<p<1$. These new inequalities are valid for the Rademacher functions or Gaussian random variables, but also for more general sequences, for example, for the analogues of such random variables in free probability. We also prove a factorization for operators from a Hilbert space to a non-commutative
$0<p<1$. These new inequalities are valid for the Rademacher functions or Gaussian random variables, but also for more general sequences, for example, for the analogues of such random variables in free probability. We also prove a factorization for operators from a Hilbert space to a non-commutative 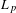 $L_{p}$-space, which is new for
$L_{p}$-space, which is new for 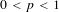 $0<p<1$. We end by showing that Mazur maps are Hölder on semifinite von Neumann algebras.
$0<p<1$. We end by showing that Mazur maps are Hölder on semifinite von Neumann algebras.