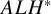 $ALH^*$
gravitational instantons
$ALH^*$
gravitational instantons
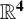 $\boldsymbol {{\mathbb {R}}^{4}}$
$\boldsymbol {{\mathbb {R}}^{4}}$