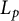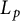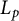1 Introduction
In [Reference Tatarko and Werner34], an
![]() $L_p$
Steiner formula was proved for the
$L_p$
Steiner formula was proved for the
![]() $L_p$
affine surface area, namely, if a convex body K is
$L_p$
affine surface area, namely, if a convex body K is
![]() $C^2_+$
, then we have, for all suitable t and for all
$C^2_+$
, then we have, for all suitable t and for all
![]() $p \in \mathbb {R}$
,
$p \in \mathbb {R}$
,
![]() $p \neq -n$
, that
$p \neq -n$
, that
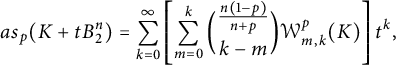 $$ \begin{align} as_p(K + t B^n_2) = \sum\limits_{k = 0}^\infty \left[ \sum\limits_{m=0}^k \binom{ \frac{n(1-p)}{n+p}}{{k-m}} {\mathcal{W}}^p_{{m}, k}(K) \right] t^k, \end{align} $$
$$ \begin{align} as_p(K + t B^n_2) = \sum\limits_{k = 0}^\infty \left[ \sum\limits_{m=0}^k \binom{ \frac{n(1-p)}{n+p}}{{k-m}} {\mathcal{W}}^p_{{m}, k}(K) \right] t^k, \end{align} $$
where
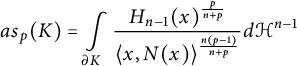 $$ \begin{align} as_p(K)= \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} d\mathcal{H}^{n-1} \end{align} $$
$$ \begin{align} as_p(K)= \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} d\mathcal{H}^{n-1} \end{align} $$
is the
![]() $L_p$
affine surface area of a convex body K,
$L_p$
affine surface area of a convex body K,
![]() $N(x)$
is the outer normal to K in
$N(x)$
is the outer normal to K in
![]() $x \in \partial K$
, the boundary of K,
$x \in \partial K$
, the boundary of K,
![]() $H_{n-1}(x)$
is the Gauss curvature in x,
$H_{n-1}(x)$
is the Gauss curvature in x,
![]() $\mathcal {H}^{n-1}$
is the usual surface area measure on
$\mathcal {H}^{n-1}$
is the usual surface area measure on
![]() $\partial K$
, and
$\partial K$
, and
![]() ${\alpha \choose k}$
are binomial coefficients (see (2.3)). The Euclidean unit ball centered at
${\alpha \choose k}$
are binomial coefficients (see (2.3)). The Euclidean unit ball centered at
![]() $0$
is denoted by
$0$
is denoted by
![]() $B^n_2$
.
$B^n_2$
.
Identity (1.1) is the analog of the classical Steiner formula (e.g., [Reference Gardner13, Reference Schneider29]) of the Brunn–Minkowski theory in the more recent
![]() $L_p$
Brunn–Minkowski theory. This theory has as its starting point Lutwak’s seminal paper [Reference Lutwak23] and it has been developed immensely (e.g., [Reference Besau, Ludwig and Werner3–Reference Böröczky, Lutwak, Yang and Zhang6, Reference Gardner, Hug, Weil and Ye14, Reference Huang, Lutwak, Yang and Zhang17, Reference Ludwig and Reitzner21, Reference Meyer and Werner24, Reference Ye41–Reference Zhao44]). In analogy to the classical theory, the coefficients
$L_p$
Brunn–Minkowski theory. This theory has as its starting point Lutwak’s seminal paper [Reference Lutwak23] and it has been developed immensely (e.g., [Reference Besau, Ludwig and Werner3–Reference Böröczky, Lutwak, Yang and Zhang6, Reference Gardner, Hug, Weil and Ye14, Reference Huang, Lutwak, Yang and Zhang17, Reference Ludwig and Reitzner21, Reference Meyer and Werner24, Reference Ye41–Reference Zhao44]). In analogy to the classical theory, the coefficients
![]() ${\mathcal {W}}^p_{{m}, k}(K) $
are called
${\mathcal {W}}^p_{{m}, k}(K) $
are called
![]() $L_p$
Steiner coefficients and they are defined in [Reference Tatarko and Werner34] for a (general) convex body K in
$L_p$
Steiner coefficients and they are defined in [Reference Tatarko and Werner34] for a (general) convex body K in
![]() $\mathbb {R}^n$
, for all
$\mathbb {R}^n$
, for all
![]() $k, m \in \mathbb {N} \cup \{0\}$
as
$k, m \in \mathbb {N} \cup \{0\}$
as
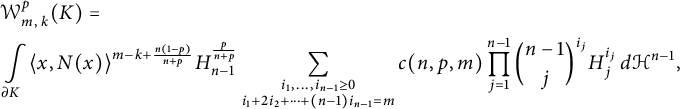 $$ \begin{align*} &\mathcal{W}^p_{m,\, k}(K) = \nonumber \\ &\int\limits_{\partial K} \langle x, N(x) \rangle^{m - k + \frac{n(1-p)}{n+p}} H_{n-1}^{\frac p{n+p}} \sum_{\substack{ i_1, \dots, i_{n-1} \geq 0 \\ i_1 + 2i_2 + \dots + (n- 1)i_{n-1}=m}} c(n, p,m) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} H_{j}^{i_j} \, d\mathcal{H}^{n-1}, \end{align*} $$
$$ \begin{align*} &\mathcal{W}^p_{m,\, k}(K) = \nonumber \\ &\int\limits_{\partial K} \langle x, N(x) \rangle^{m - k + \frac{n(1-p)}{n+p}} H_{n-1}^{\frac p{n+p}} \sum_{\substack{ i_1, \dots, i_{n-1} \geq 0 \\ i_1 + 2i_2 + \dots + (n- 1)i_{n-1}=m}} c(n, p,m) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} H_{j}^{i_j} \, d\mathcal{H}^{n-1}, \end{align*} $$
where the
![]() $H_j$
are the jth normalized elementary symmetric functions of the principal curvatures. The
$H_j$
are the jth normalized elementary symmetric functions of the principal curvatures. The
![]() $c(n, p,m)$
are certain binomial coefficients (see [Reference Tatarko and Werner34, Reference Tatarko and Werner35] for the details). The
$c(n, p,m)$
are certain binomial coefficients (see [Reference Tatarko and Werner34, Reference Tatarko and Werner35] for the details). The
![]() $L_p$
Steiner coefficients were studied in [Reference Tatarko and Werner35], where it was proved, among other results, that they are valuations on the set of convex bodies.
$L_p$
Steiner coefficients were studied in [Reference Tatarko and Werner35], where it was proved, among other results, that they are valuations on the set of convex bodies.
1.1 Main results
In this paper, we look at the
![]() $L_p$
Steiner formula with a different focus. Expressions also appearing naturally in formula (1.1) are weighted
$L_p$
Steiner formula with a different focus. Expressions also appearing naturally in formula (1.1) are weighted
![]() $L_p$
affine surface areas,
$L_p$
affine surface areas,
![]() $ \mu _{\vec {i}}-as_p(K)$
, which we define in Section 2.2.
$ \mu _{\vec {i}}-as_p(K)$
, which we define in Section 2.2.
We investigate in detail those weighted
![]() $L_p$
affine surface areas in Section 3. We show that they are homogeneous of a certain degree and are invariant under rotations and reflections. We show that they are valuations on the set of convex bodies. Valuations have become a vitally import subject of study in convexity and affine and differential geometry (e.g., [Reference Alesker1, Reference Colesanti, Ludwig and Mussnig10, Reference Haberl15, Reference Haberl and Parapatits16, Reference Ludwig22, Reference Schuster30]). The weighted
$L_p$
affine surface areas in Section 3. We show that they are homogeneous of a certain degree and are invariant under rotations and reflections. We show that they are valuations on the set of convex bodies. Valuations have become a vitally import subject of study in convexity and affine and differential geometry (e.g., [Reference Alesker1, Reference Colesanti, Ludwig and Mussnig10, Reference Haberl15, Reference Haberl and Parapatits16, Reference Ludwig22, Reference Schuster30]). The weighted
![]() $L_p$
affine surface areas satisfy isoperimetric inequalities which generalize the
$L_p$
affine surface areas satisfy isoperimetric inequalities which generalize the
![]() $L_p$
affine isoperimetric inequalities of [Reference Lutwak23, Reference Werner and Ye39]. This is shown in Theorem 3.2.
$L_p$
affine isoperimetric inequalities of [Reference Lutwak23, Reference Werner and Ye39]. This is shown in Theorem 3.2.
Theorem 3.2 Let
![]() $s\neq -n, r \neq -n, t \neq -n$
be real numbers. Let K be a
$s\neq -n, r \neq -n, t \neq -n$
be real numbers. Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin.
$\mathbb R^n$
with centroid at the origin.
(i) If
![]() $\frac {(n+r)(t-s)}{(n+t)(r-s)}>1$
, then
$\frac {(n+r)(t-s)}{(n+t)(r-s)}>1$
, then
(ii) If
![]() $\frac {(n+r)t}{(n+t)r}>1$
, then
$\frac {(n+r)t}{(n+t)r}>1$
, then
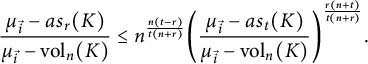 $$ \begin{align*}\frac{\mu_{\vec{i}} - as_r(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\leq n^{\frac{n(t-r)}{t(n+r)}} \bigg(\frac{\mu_{\vec{i}} - as_t(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\bigg)^{\frac{r(n+t)}{{t(n+r)}}}. \end{align*} $$
$$ \begin{align*}\frac{\mu_{\vec{i}} - as_r(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\leq n^{\frac{n(t-r)}{t(n+r)}} \bigg(\frac{\mu_{\vec{i}} - as_t(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\bigg)^{\frac{r(n+t)}{{t(n+r)}}}. \end{align*} $$
Equality holds in the above inequalities, if and only if K is an ellipsoid.
We show in Section 3.3, that the weighted
![]() $L_p$
affine surface areas have natural geometric interpretations in terms of certain convex bodies associated with the given convex body K.
$L_p$
affine surface areas have natural geometric interpretations in terms of certain convex bodies associated with the given convex body K.
We prove a monotonicity behavior in the parameter p for the weighted
![]() $L_p$
affine surface areas which allows to establish asymptotics for the weighted
$L_p$
affine surface areas which allows to establish asymptotics for the weighted
![]() $L_p$
affine surface areas. These asymptotics connects them to entropy powers, namely to the Kullbak–Leibler divergence
$L_p$
affine surface areas. These asymptotics connects them to entropy powers, namely to the Kullbak–Leibler divergence
![]() $D_{KL}$
of the cone measures of K and its polar
$D_{KL}$
of the cone measures of K and its polar
![]() $K^\circ $
,
$K^\circ $
,
![]() $Q_K,$
and
$Q_K,$
and
![]() $P_K$
. We quote the relevant Theorem 3.8 and refer to Section 3.4 for the details. We put
$P_K$
. We quote the relevant Theorem 3.8 and refer to Section 3.4 for the details. We put
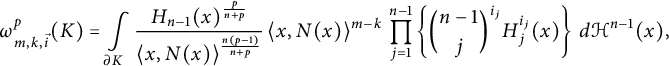 $$ \begin{align*} \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x), \end{align*} $$
$$ \begin{align*} \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x), \end{align*} $$
and then the following theorem holds.
Theorem 3.8 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin. Then,
$\mathbb R^n$
with centroid at the origin. Then,
-
(i)
 $$ \begin{align*} \lim\limits_{p \rightarrow \infty} \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_K||Q_K)}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
$$ \begin{align*} \lim\limits_{p \rightarrow \infty} \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_K||Q_K)}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
-
(ii)
 $$ \begin{align*} \lim\limits_{p \rightarrow 0} \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_{K^\circ}||Q_{K^\circ})}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
$$ \begin{align*} \lim\limits_{p \rightarrow 0} \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_{K^\circ}||Q_{K^\circ})}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
This leads naturally to consider more general f-divergences than just the Kullbak–Leibler divergence. We treat that in Section 4, where we also observe that the weighted
![]() $L_p$
affine surface areas themselves are special f-divergences.
$L_p$
affine surface areas themselves are special f-divergences.
Throughout the paper, we assume that the convex bodies K are
![]() $C^2_+$
, i.e., K has twice continuously differentiable boundary with strictly positive Gauss curvature everywhere and such that
$C^2_+$
, i.e., K has twice continuously differentiable boundary with strictly positive Gauss curvature everywhere and such that
![]() $0$
is the centroid of K,
$0$
is the centroid of K,
![]() $0 = \frac {1}{{\mathrm {vol}}_n(K)} \int _{K} xdx$
.
$0 = \frac {1}{{\mathrm {vol}}_n(K)} \int _{K} xdx$
.
2 Weighted
 $L_p$
-affine surface areas
$L_p$
-affine surface areas
2.1 Background from differential geometry
For more information and the details in this section, we refer to, e.g., [Reference Gardner13, Reference Schneider29].
Let K be a convex body of class
![]() $C^2.$
For a point x on the boundary
$C^2.$
For a point x on the boundary
![]() $\partial K$
of
$\partial K$
of
![]() $K,$
we denote by
$K,$
we denote by
![]() $N(x)$
the unique outward unit normal vector of K at
$N(x)$
the unique outward unit normal vector of K at
![]() $x.$
The map
$x.$
The map
![]() $N_K: \partial K \to S^{n - 1}$
is called the spherical image map or Gauss map of K and is of class
$N_K: \partial K \to S^{n - 1}$
is called the spherical image map or Gauss map of K and is of class
![]() $C^1.$
Its differential is called the Weingarten map. The eigenvalues of the Weingarten map are the principal curvatures
$C^1.$
Its differential is called the Weingarten map. The eigenvalues of the Weingarten map are the principal curvatures
![]() $k_i(x)$
of K at
$k_i(x)$
of K at
![]() $x.$
$x.$
The jth normalized elementary symmetric functions of the principal curvatures are denoted by
![]() $H_j$
. They are defined as follows:
$H_j$
. They are defined as follows:
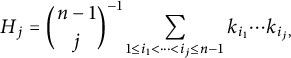 $$ \begin{align} H_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} k_{i_1} \cdots k_{i_j,} \end{align} $$
$$ \begin{align} H_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} k_{i_1} \cdots k_{i_j,} \end{align} $$
for
![]() $j = 1, \dots , n-1$
and
$j = 1, \dots , n-1$
and
![]() $H_0 = 1.$
Note that
$H_0 = 1.$
Note that
is the mean curvature, that is, the average of principal curvatures, and
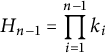 $$ \begin{align*}H_{n - 1}= \prod_{i=1}^{n-1} k_i\end{align*} $$
$$ \begin{align*}H_{n - 1}= \prod_{i=1}^{n-1} k_i\end{align*} $$
is the Gauss curvature.
We say that K is of class
![]() $C^2_+$
if K is of class
$C^2_+$
if K is of class
![]() $C^2$
and the Gauss map
$C^2$
and the Gauss map
![]() $\nu $
is a diffeomorphism. This means in particular that
$\nu $
is a diffeomorphism. This means in particular that
![]() $N_K$
has a smooth inverse. This assumption is stronger than just
$N_K$
has a smooth inverse. This assumption is stronger than just
![]() $C^2,$
and is equivalent to the assumption that all principal curvatures are strictly positive, or that the Gauss curvature
$C^2,$
and is equivalent to the assumption that all principal curvatures are strictly positive, or that the Gauss curvature
![]() $H_{n-1} \ne 0.$
It also means that the differential of
$H_{n-1} \ne 0.$
It also means that the differential of
![]() $N_K$
, i.e., the Weingarten map, is of maximal rank everywhere.
$N_K$
, i.e., the Weingarten map, is of maximal rank everywhere.
Let K be of class
![]() $C^2_+$
. For
$C^2_+$
. For
![]() $u \in {\mathbb {R}}^n \setminus \{0\}$
, let
$u \in {\mathbb {R}}^n \setminus \{0\}$
, let
![]() $\xi _K(u)$
be the unique point on the boundary of K at which u is an outward normal vector. The map
$\xi _K(u)$
be the unique point on the boundary of K at which u is an outward normal vector. The map
![]() $\xi _K$
is defined on
$\xi _K$
is defined on
![]() ${\mathbb {R}}^n \setminus \{0\}$
. Its restriction to the sphere
${\mathbb {R}}^n \setminus \{0\}$
. Its restriction to the sphere
![]() $S^{n - 1},$
the map
$S^{n - 1},$
the map
![]() $\bar {\xi }_K: S^{n - 1} \to \partial K$
, is called the reverse spherical image map, or reverse Gauss map. The differential of
$\bar {\xi }_K: S^{n - 1} \to \partial K$
, is called the reverse spherical image map, or reverse Gauss map. The differential of
![]() $\bar {\xi }_K$
is called the reverse Weingarten map. The eigenvalues of the reverse Weingarten map are called the principal radii of curvature
$\bar {\xi }_K$
is called the reverse Weingarten map. The eigenvalues of the reverse Weingarten map are called the principal radii of curvature
![]() $r_1, \dots , r_{n - 1}$
of K at
$r_1, \dots , r_{n - 1}$
of K at
![]() $u\in S^{n - 1}.$
$u\in S^{n - 1}.$
The jth normalized elementary symmetric functions of the principal radii of curvature are denoted by
![]() $s_j$
. In particular,
$s_j$
. In particular,
![]() $s_0=1$
, and for
$s_0=1$
, and for
![]() $1 \leq j \leq n-1,$
they are defined by
$1 \leq j \leq n-1,$
they are defined by
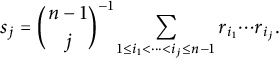 $$ \begin{align} s_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} r_{i_1} \cdots r_{i_j}. \end{align} $$
$$ \begin{align} s_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} r_{i_1} \cdots r_{i_j}. \end{align} $$
Note that the principal curvatures are functions on the boundary of K and the principal radii of curvature are functions on the sphere.
Now, we describe the connection between
![]() $H_j$
and
$H_j$
and
![]() $s_j.$
For a body K of class
$s_j.$
For a body K of class
![]() $C^2_+$
, we have for
$C^2_+$
, we have for
![]() $u\in S^{n - 1}$
that
$u\in S^{n - 1}$
that
![]() $\bar {\xi }_K(u) = N_K^{-1}(u)$
. In particular, the principal radii of curvature are reciprocals of the principal curvatures, that is,
$\bar {\xi }_K(u) = N_K^{-1}(u)$
. In particular, the principal radii of curvature are reciprocals of the principal curvatures, that is,
This implies that for
![]() $x \in \partial K$
with
$x \in \partial K$
with
![]() $N_K(x)=u$
,
$N_K(x)=u$
,
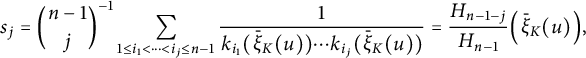 $$ \begin{align*}s_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} \frac1{k_{i_1}(\bar{\xi}_K(u)) \cdots k_{i_j}(\bar{\xi}_K(u))} = \frac{H_{n - 1 -j}}{H_{n - 1}}\Big(\bar{\xi}_K(u)\Big), \end{align*} $$
$$ \begin{align*}s_j = {n - 1 \choose j}^{-1} \sum_{1\leq i_1 < \dots < i_j \leq n - 1} \frac1{k_{i_1}(\bar{\xi}_K(u)) \cdots k_{i_j}(\bar{\xi}_K(u))} = \frac{H_{n - 1 -j}}{H_{n - 1}}\Big(\bar{\xi}_K(u)\Big), \end{align*} $$
and
for
![]() $j = 1, \dots , n-1.$
$j = 1, \dots , n-1.$
2.2 Definitions
For
![]() $\alpha \in \mathbb {R}$
and
$\alpha \in \mathbb {R}$
and
![]() $k \in \mathbb {N}$
, the generalized binomial coefficients are defined as
$k \in \mathbb {N}$
, the generalized binomial coefficients are defined as
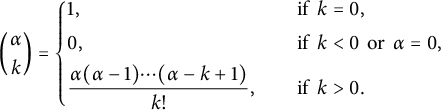 $$ \begin{align} {\alpha \choose k} = \left\{\vphantom{\begin{array}{@{\!\!\!\!\!\!\!\!}lll}&1, &\qquad\text{if }\, k=0,\\[2pt] &0, &\qquad\text{if }\, k<0 \, \text{ or }\, \alpha =0,\\[4pt] &\dfrac{\alpha(\alpha - 1)\cdots(\alpha - k + 1)}{k!}, &\qquad\text{if }\, k> 0. \end{array}_{}}\begin{array}{@{\kern-1pt\!\!\!\!\!\!}lll}&1, &\quad\text{if }\, k=0,\\[4pt] &0, &\quad\text{if }\, k<0 \, \text{ or }\, \alpha =0,\\[4pt] &\dfrac{\alpha(\alpha - 1)\cdots(\alpha - k + 1)}{k!}, &\quad\text{if }\, k> 0. \end{array}\right. \end{align} $$
$$ \begin{align} {\alpha \choose k} = \left\{\vphantom{\begin{array}{@{\!\!\!\!\!\!\!\!}lll}&1, &\qquad\text{if }\, k=0,\\[2pt] &0, &\qquad\text{if }\, k<0 \, \text{ or }\, \alpha =0,\\[4pt] &\dfrac{\alpha(\alpha - 1)\cdots(\alpha - k + 1)}{k!}, &\qquad\text{if }\, k> 0. \end{array}_{}}\begin{array}{@{\kern-1pt\!\!\!\!\!\!}lll}&1, &\quad\text{if }\, k=0,\\[4pt] &0, &\quad\text{if }\, k<0 \, \text{ or }\, \alpha =0,\\[4pt] &\dfrac{\alpha(\alpha - 1)\cdots(\alpha - k + 1)}{k!}, &\quad\text{if }\, k> 0. \end{array}\right. \end{align} $$
For fixed
![]() $k \in \mathbb {N}$
,
$k \in \mathbb {N}$
,
![]() $m\in \mathbb {N} \cup \{0\}$
and fixed sequence
$m\in \mathbb {N} \cup \{0\}$
and fixed sequence
![]() $\vec {i}=\{i_j\}_{j=0}^{n-1}$
such that
$\vec {i}=\{i_j\}_{j=0}^{n-1}$
such that
![]() $i_1+2 i_2+ \cdots (n-1) i_{n-1} =m$
and all
$i_1+2 i_2+ \cdots (n-1) i_{n-1} =m$
and all
![]() $p \in \mathbb {R}$
,
$p \in \mathbb {R}$
,
![]() $p \neq -n$
, we define
$p \neq -n$
, we define
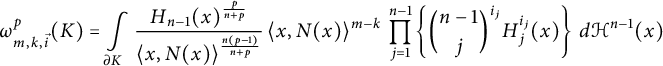 $$ \begin{align} \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \end{align} $$
$$ \begin{align} \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \end{align} $$
and
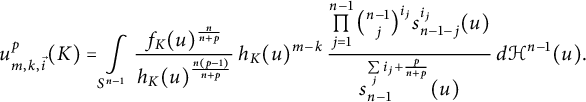 $$ \begin{align} u_{m,k,\vec{i}}^p (K) = \int\limits_{S^{n-1}}\frac{f_{K}(u)^{\frac{n}{n+p}}} {h_K(u) ^{\frac{n(p-1)}{n+p}}} \, h_K(u) ^{m-k} \, \frac{ \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} \, d\mathcal{H}^{n-1}(u). \end{align} $$
$$ \begin{align} u_{m,k,\vec{i}}^p (K) = \int\limits_{S^{n-1}}\frac{f_{K}(u)^{\frac{n}{n+p}}} {h_K(u) ^{\frac{n(p-1)}{n+p}}} \, h_K(u) ^{m-k} \, \frac{ \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} \, d\mathcal{H}^{n-1}(u). \end{align} $$
Remark 2.1 Note that the above quantities are vanishing for polytopes. Therefore, we will treat only
![]() $C^2_+$
convex bodies throughout the text and then
$C^2_+$
convex bodies throughout the text and then
Denote
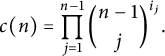 $$ \begin{align*}c(n) = \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j}. \end{align*} $$
$$ \begin{align*}c(n) = \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j}. \end{align*} $$
Let
![]() $\mu _{m,k,\vec {i}}$
be the measure on
$\mu _{m,k,\vec {i}}$
be the measure on
![]() $\partial K$
with density
$\partial K$
with density
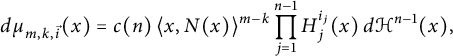 $$ \begin{align*}d\mu_{m,k,\vec{i}} (x) = c(n) \, \langle x,N(x)\rangle^{m-k} \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x)\, d\mathcal{H}^{n-1}(x), \end{align*} $$
$$ \begin{align*}d\mu_{m,k,\vec{i}} (x) = c(n) \, \langle x,N(x)\rangle^{m-k} \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x)\, d\mathcal{H}^{n-1}(x), \end{align*} $$
with respect to the surface measure
![]() $\mathcal {H}^{n-1}$
on
$\mathcal {H}^{n-1}$
on
![]() $\partial K,$
and let
$\partial K,$
and let
![]() $\nu _{m,k,\vec {i}}$
be the measure on
$\nu _{m,k,\vec {i}}$
be the measure on
![]() $S^{n-1}$
with density
$S^{n-1}$
with density
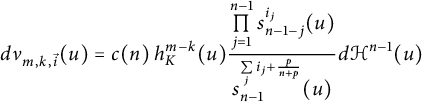 $$ \begin{align*}d\nu_{m,k,\vec{i}} (u) =c(n) \, h^{m-k}_K(u) \frac{\prod\limits_{j = 1}^{n - 1}s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} d\mathcal{H}^{n-1}(u) \end{align*} $$
$$ \begin{align*}d\nu_{m,k,\vec{i}} (u) =c(n) \, h^{m-k}_K(u) \frac{\prod\limits_{j = 1}^{n - 1}s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} d\mathcal{H}^{n-1}(u) \end{align*} $$
with respect to the surface measure
![]() $\mathcal {H}^{n-1}$
on
$\mathcal {H}^{n-1}$
on
![]() $S^{n-1}$
. To keep notations simple, we mostly write
$S^{n-1}$
. To keep notations simple, we mostly write
![]() $\mu _{\vec {i}}$
and
$\mu _{\vec {i}}$
and
![]() $\nu _{\vec {i}}$
instead of
$\nu _{\vec {i}}$
instead of
![]() $\mu _{m,k,\vec {i}}$
and
$\mu _{m,k,\vec {i}}$
and
![]() $\nu _{m,k,\vec {i}}$
.
$\nu _{m,k,\vec {i}}$
.
We then define the weighted
![]() $L_p$
-affine surface areas by
$L_p$
-affine surface areas by
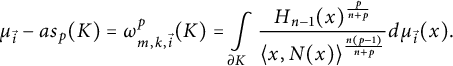 $$ \begin{align} \mu_{\vec{i}} - as_p(K)= \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} d\mu_{\vec{i}}(x). \end{align} $$
$$ \begin{align} \mu_{\vec{i}} - as_p(K)= \omega_{m,k,\vec{i}}^p (K) = \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} d\mu_{\vec{i}}(x). \end{align} $$
Definition (1.2) explains that those can be considered as
![]() $L_p$
-affine surface area weighted by the measure
$L_p$
-affine surface area weighted by the measure
![]() $\mu _{\vec {i}}$
. In particular,
$\mu _{\vec {i}}$
. In particular,
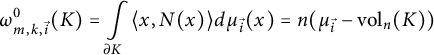 $$ \begin{align*}\omega_{m,k,\vec{i}}^0 (K) = \int\limits_{\partial K} \langle x,N(x)\rangle d\mu_{\vec{i}}(x) = n(\mu_{\vec{i}}-{\mathrm{vol}}_n(K)) \end{align*} $$
$$ \begin{align*}\omega_{m,k,\vec{i}}^0 (K) = \int\limits_{\partial K} \langle x,N(x)\rangle d\mu_{\vec{i}}(x) = n(\mu_{\vec{i}}-{\mathrm{vol}}_n(K)) \end{align*} $$
is a weighted volume of K, weighted by the measure
![]() $\mu _{\vec {i}}$
and
$\mu _{\vec {i}}$
and
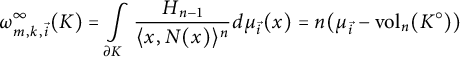 $$ \begin{align*}\omega_{m,k,\vec{i}}^\infty (K) = \int\limits_{\partial K} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} d\mu_{\vec{i}}(x) =n( \mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)) \end{align*} $$
$$ \begin{align*}\omega_{m,k,\vec{i}}^\infty (K) = \int\limits_{\partial K} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} d\mu_{\vec{i}}(x) =n( \mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)) \end{align*} $$
is a weighted volume of
![]() $K^\circ $
, weighted by the measure
$K^\circ $
, weighted by the measure
![]() $\mu _{\vec {i}}$
, where
$\mu _{\vec {i}}$
, where
is the polar body of K.
We can take another point of view for the measure
![]() $d\mathcal {H}^{n-1}$
on
$d\mathcal {H}^{n-1}$
on
![]() $S^{n-1}$
via the density
$S^{n-1}$
via the density
 $f_p(K,u) = \left (\frac {f_K(u)}{h_K^{p-1}(u)}\right )^{\frac n{n+p}}$
. This density was introduced by Lutwak [Reference Lutwak23]. Then
$f_p(K,u) = \left (\frac {f_K(u)}{h_K^{p-1}(u)}\right )^{\frac n{n+p}}$
. This density was introduced by Lutwak [Reference Lutwak23]. Then
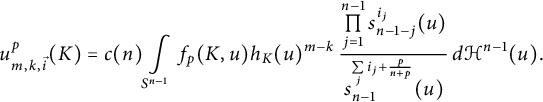 $$ \begin{align*}u_{m,k,\vec{i}}^p (K) = c(n) \int\limits_{S^{n-1}} f_p(K,u) h_K(u) ^{m-k} \, \frac{ \prod\limits_{j = 1}^{n - 1} s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} \, d\mathcal{H}^{n-1}(u). \end{align*} $$
$$ \begin{align*}u_{m,k,\vec{i}}^p (K) = c(n) \int\limits_{S^{n-1}} f_p(K,u) h_K(u) ^{m-k} \, \frac{ \prod\limits_{j = 1}^{n - 1} s_{n-1-j}^{i_j} (u)}{s_{n-1}^{\sum\limits_j i_j+\frac p{n+p}}(u)} \, d\mathcal{H}^{n-1}(u). \end{align*} $$
2.3 Special cases
Note that
where we denote the sequence
![]() $\vec {i} = \{0, \dots , 0\}$
as
$\vec {i} = \{0, \dots , 0\}$
as
![]() $0$
.
$0$
.
1. When
![]() $k = m$
, we get
$k = m$
, we get
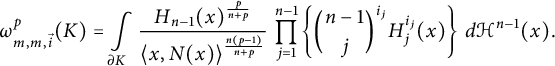 $$ \begin{align*}\omega_{m,m,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x). \end{align*} $$
$$ \begin{align*}\omega_{m,m,\vec{i}}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x). \end{align*} $$
2.
![]() $m = 0$
implies that
$m = 0$
implies that
![]() $\vec {i} = 0$
and (2.4) simplifies to
$\vec {i} = 0$
and (2.4) simplifies to
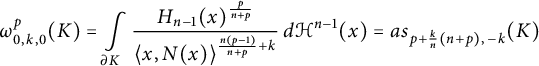 $$ \begin{align*}\omega_{0,k,0}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}+k}} \, d\mathcal{H}^{n-1}(x) = as_{p + \frac kn (n+p),\, -k}(K) \end{align*} $$
$$ \begin{align*}\omega_{0,k,0}^p (K) = \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}+k}} \, d\mathcal{H}^{n-1}(x) = as_{p + \frac kn (n+p),\, -k}(K) \end{align*} $$
(see [Reference Tatarko and Werner34, equation (29)]).
3. For the Euclidean unit ball
![]() $B^n_2$
, we get
$B^n_2$
, we get
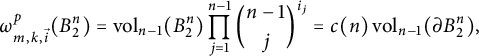 $$ \begin{align} \omega_{m,k,\vec{i}}^p (B^n_2) = {\mathrm{vol}}_{n-1}(B^n_2) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} = c(n)\, {\mathrm{vol}}_{n-1}(\partial B^n_2), \end{align} $$
$$ \begin{align} \omega_{m,k,\vec{i}}^p (B^n_2) = {\mathrm{vol}}_{n-1}(B^n_2) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} = c(n)\, {\mathrm{vol}}_{n-1}(\partial B^n_2), \end{align} $$
which does not depend on k. Note that if
![]() $i_0 \ne 0$
and
$i_0 \ne 0$
and
![]() $i_1 = \dots = i_{n-1} = 0$
, that is,
$i_1 = \dots = i_{n-1} = 0$
, that is,
![]() ${\vec {i} = \{i_0, 0, \dots , 0\}}$
, then
${\vec {i} = \{i_0, 0, \dots , 0\}}$
, then
![]() $\omega _{m,k,\vec {i}}^p (B^n_2) = {\mathrm {vol}}_{n-1}(\partial B^n_2)$
.
$\omega _{m,k,\vec {i}}^p (B^n_2) = {\mathrm {vol}}_{n-1}(\partial B^n_2)$
.
4. If
![]() $p = 0$
, we have
$p = 0$
, we have
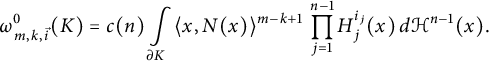 $$ \begin{align*}\omega_{m,k, \vec{i}}^0(K) = c(n) \int\limits_{\partial K} \langle x,N(x)\rangle ^{m-k+1} \, \prod\limits_{j = 1}^{n - 1}H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
$$ \begin{align*}\omega_{m,k, \vec{i}}^0(K) = c(n) \int\limits_{\partial K} \langle x,N(x)\rangle ^{m-k+1} \, \prod\limits_{j = 1}^{n - 1}H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
When in addition
![]() $k = m$
, we get
$k = m$
, we get
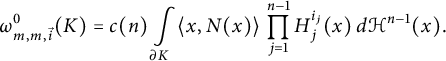 $$ \begin{align*}\omega_{m,m, \vec{i}}^0(K) = c(n) \int\limits_{\partial K} \langle x,N(x)\rangle \, \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
$$ \begin{align*}\omega_{m,m, \vec{i}}^0(K) = c(n) \int\limits_{\partial K} \langle x,N(x)\rangle \, \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
5. If
![]() $p = \infty $
, we get that
$p = \infty $
, we get that
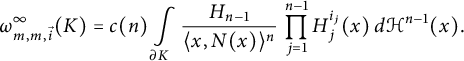 $$ \begin{align*}\omega_{m,m, \vec{i}}^\infty(K) = c(n) \int\limits_{\partial K} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \, \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
$$ \begin{align*}\omega_{m,m, \vec{i}}^\infty(K) = c(n) \int\limits_{\partial K} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \, \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}(x) \, d\mathcal{H}^{n-1}(x). \end{align*} $$
3 Properties of the weighted
 $L_p$
-affine surface areas
$L_p$
-affine surface areas
3.1 Valuation, invariance, and homogeneity
Proposition 3.1 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin. Let
$\mathbb R^n$
with centroid at the origin. Let
![]() $p \in \mathbb {R}$
,
$p \in \mathbb {R}$
,
![]() $p\neq -n$
. Then
$p\neq -n$
. Then
![]() $\omega _{m,k,\vec {i}}^p (K)$
is an
$\omega _{m,k,\vec {i}}^p (K)$
is an
![]() $\left (n\frac {n-p}{n+p}-k\right )$
-homogeneous valuation that is invariant under rotations and reflections.
$\left (n\frac {n-p}{n+p}-k\right )$
-homogeneous valuation that is invariant under rotations and reflections.
Proof The proof follows immediately from results in [Reference Tatarko and Werner35]. We present an outline of the proof for completeness.
1. Valuation. As was shown in [Reference Tatarko and Werner35, Theorem 5.9], for all
![]() $1 \leq i_1, \dots , i_{n-1} \leq n-1$
,
$1 \leq i_1, \dots , i_{n-1} \leq n-1$
,
![]() $1\leq j \leq n-1$
, and
$1\leq j \leq n-1$
, and
![]() $\alpha _1, \dots , \alpha _{j} \geq 0$
,
$\alpha _1, \dots , \alpha _{j} \geq 0$
,
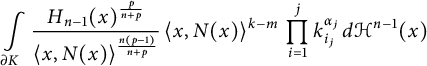 $$ \begin{align*}\int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{k-m} \, \prod\limits_{i = 1}^{j} k_{i_j}^{\alpha_j}\, d\mathcal{H}^{n-1}(x) \end{align*} $$
$$ \begin{align*}\int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{k-m} \, \prod\limits_{i = 1}^{j} k_{i_j}^{\alpha_j}\, d\mathcal{H}^{n-1}(x) \end{align*} $$
is a valuation. It immediately follows that
![]() $ \omega _{m,k,\vec {i}}^p (K) $
are valuations as the linear combination of valuations is again a valuation.
$ \omega _{m,k,\vec {i}}^p (K) $
are valuations as the linear combination of valuations is again a valuation.
2. Homogeneity. Similarly to [Reference Tatarko and Werner35, Theorem 5.1] we can show that
![]() $\omega _{m, k, \vec {i}}^p (K)$
are homogeneous of order
$\omega _{m, k, \vec {i}}^p (K)$
are homogeneous of order
![]() $n\frac {n-p}{n+p} - k$
. Applying [Reference Tatarko and Werner35, Proposition 5.4] with
$n\frac {n-p}{n+p} - k$
. Applying [Reference Tatarko and Werner35, Proposition 5.4] with
![]() $T = a\, Id$
, we get that
$T = a\, Id$
, we get that
![]() $\omega _{m, k, \vec {i}}^p (K) = a^{k - n\frac {n-p}{n+p}} \omega _{m, k, \vec {i}}^p (aK)$
.
$\omega _{m, k, \vec {i}}^p (K) = a^{k - n\frac {n-p}{n+p}} \omega _{m, k, \vec {i}}^p (aK)$
.
3. Invariance. If T is a rotation or a reflection, then
![]() $|\det T|=1$
,
$|\det T|=1$
,
![]() $\|T^{-1t}(N_{ K}(T^{-1}(y)))\| = \| N_{ K}(T^{-1}(y))\| = 1$
and for all
$\|T^{-1t}(N_{ K}(T^{-1}(y)))\| = \| N_{ K}(T^{-1}(y))\| = 1$
and for all
![]() $1 \leq j \leq n-1$
,
$1 \leq j \leq n-1$
,
Thus, using these observations and [Reference Tatarko and Werner35, Proposition 5.4], we get
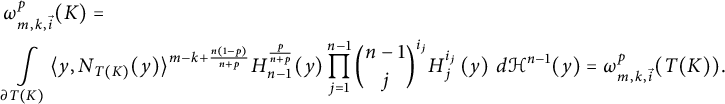 $$ \begin{align*} &\omega_{m, k, \vec{i}}^p (K) =\\ & \int\limits_{\partial T(K)} \langle y, N_{T(K)}(y) \rangle^{m - k + \frac{n(1-p)}{n+p}} H_{n-1}^{\frac p{n+p}} (y) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} H_{j}^{i_j}\left(y \right) \, d\mathcal{H}^{n-1}(y) = \omega_{m, k, \vec{i}}^p (T(K)). \end{align*} $$
$$ \begin{align*} &\omega_{m, k, \vec{i}}^p (K) =\\ & \int\limits_{\partial T(K)} \langle y, N_{T(K)}(y) \rangle^{m - k + \frac{n(1-p)}{n+p}} H_{n-1}^{\frac p{n+p}} (y) \prod\limits_{j = 1}^{n - 1} {n - 1\choose j}^{i_j} H_{j}^{i_j}\left(y \right) \, d\mathcal{H}^{n-1}(y) = \omega_{m, k, \vec{i}}^p (T(K)). \end{align*} $$
3.2 Inequalities
Theorem 3.2 Let
![]() $s\neq -n, r \neq -n, t \neq -n$
be real numbers. Let K be a
$s\neq -n, r \neq -n, t \neq -n$
be real numbers. Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin.
$\mathbb R^n$
with centroid at the origin.
-
(i) If
 $\frac {(n+r)(t-s)}{(n+t)(r-s)}>1$
, then
$\frac {(n+r)(t-s)}{(n+t)(r-s)}>1$
, then  $$ \begin{align*} \mu_{\vec{i}} - as_r(K) \leq \big(\mu_{\vec{i}} - as_t(K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\mu_{\vec{i}} - as_s(K) \big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}. \end{align*} $$
$$ \begin{align*} \mu_{\vec{i}} - as_r(K) \leq \big(\mu_{\vec{i}} - as_t(K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\mu_{\vec{i}} - as_s(K) \big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}. \end{align*} $$
-
(ii) If
 $\frac {(n+r)t}{(n+t)r}>1$
, then Equality holds in the above inequalities, if and only if K is an ellipsoid.
$\frac {(n+r)t}{(n+t)r}>1$
, then Equality holds in the above inequalities, if and only if K is an ellipsoid. $$ \begin{align*}\frac{\mu_{\vec{i}} - as_r(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\leq n^{\frac{n(t-r)}{t(n+r)}} \bigg(\frac{\mu_{\vec{i}} - as_t(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\bigg)^{\frac{r(n+t)}{{t(n+r)}}}. \end{align*} $$
$$ \begin{align*}\frac{\mu_{\vec{i}} - as_r(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\leq n^{\frac{n(t-r)}{t(n+r)}} \bigg(\frac{\mu_{\vec{i}} - as_t(K)}{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)}\bigg)^{\frac{r(n+t)}{{t(n+r)}}}. \end{align*} $$
Proof
(i) By Hölder’s inequality—which enforces the condition
![]() $\frac {(n+r)(s-t)}{(n+t)(s-r)}>1$
, we then get
$\frac {(n+r)(s-t)}{(n+t)(s-r)}>1$
, we then get
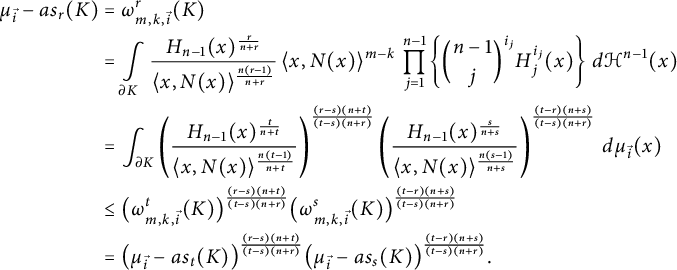 $$ \begin{align} \mu_{\vec{i}} - as_r(K) &= \omega_{m,k,\vec{i}}^r (K) \\ &= \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{r}{n+r}}} {\langle x,N(x)\rangle ^{\frac{n(r-1)}{n+r}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \nonumber \\ &= \int _{\partial K} \left(\frac{H_{n-1}(x)^{\frac{t}{n+t}}}{\langle x, N(x)\rangle ^{\frac{n(t-1)}{n+t}}} \right)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \left(\frac{H_{n-1}(x)^{\frac{s}{n+s}}}{\langle x, N(x)\rangle ^{\frac{n(s-1)}{n+s}}}\right)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}\, d\mu_{\vec{i}}(x) \nonumber \\ &\leq \big(\omega_{m,k,\vec{i}}^t (K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\omega_{m,k,\vec{i}}^s (K)\big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}} \nonumber \\ &= \big(\mu_{\vec{i}} - as_t(K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\mu_{\vec{i}} - as_s(K) \big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}. \nonumber \end{align} $$
$$ \begin{align} \mu_{\vec{i}} - as_r(K) &= \omega_{m,k,\vec{i}}^r (K) \\ &= \int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{r}{n+r}}} {\langle x,N(x)\rangle ^{\frac{n(r-1)}{n+r}}} \,\langle x,N(x)\rangle ^{m-k} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \nonumber \\ &= \int _{\partial K} \left(\frac{H_{n-1}(x)^{\frac{t}{n+t}}}{\langle x, N(x)\rangle ^{\frac{n(t-1)}{n+t}}} \right)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \left(\frac{H_{n-1}(x)^{\frac{s}{n+s}}}{\langle x, N(x)\rangle ^{\frac{n(s-1)}{n+s}}}\right)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}\, d\mu_{\vec{i}}(x) \nonumber \\ &\leq \big(\omega_{m,k,\vec{i}}^t (K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\omega_{m,k,\vec{i}}^s (K)\big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}} \nonumber \\ &= \big(\mu_{\vec{i}} - as_t(K) \big)^{\frac{(r-s)(n+t)}{(t-s)(n+r)}} \big(\mu_{\vec{i}} - as_s(K) \big)^{\frac{(t-r)(n+s)}{(t-s)(n+r)}}. \nonumber \end{align} $$
(ii) Similarly, again using Hölder’s inequality—which now enforces the condition
![]() $~\frac {(n+r)t}{(n+t)r}>1,~$
$~\frac {(n+r)t}{(n+t)r}>1,~$
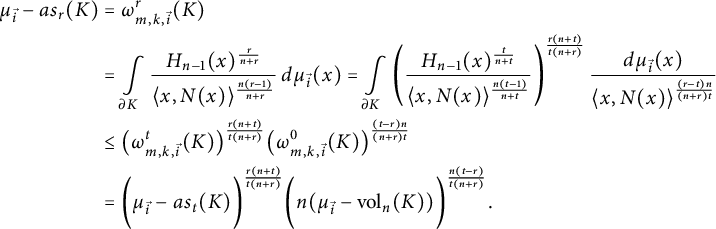 $$ \begin{align*} \mu_{\vec{i}} - as_r(K) &=\omega_{m,k,\vec{i}}^r(K)\\ &=\int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{r}{n+r}}}{\langle x, N(x)\rangle ^{\frac{n(r-1)}{n+r}}}\, d\mu_{\vec{i}} (x) = \int\limits_{\partial K} \left(\frac{H_{n-1}(x)^{\frac{t}{n+t}}}{\langle x, N(x)\rangle ^{\frac{n(t-1)}{n+t}}} \right)^{\frac{r(n+t)}{t(n+r)}} \frac{d\mu_{\vec{i}} (x)}{\langle x, N(x)\rangle ^{\frac{(r-t)n}{(n+r)t}}} \\ &\leq \big(\omega_{m,k,\vec{i}}^t(K)\big)^{\frac{r(n+t)}{t(n+r)}} \big( \omega_{m,k,\vec{i}}^0(K)\big)^{\frac{(t-r)n}{(n+r)t}} \nonumber \\ &= \bigg(\mu_{\vec{i}} - as_t(K)\bigg)^{\frac{r(n+t)}{{t(n+r)}}} \bigg(n(\mu_{\vec{i}}-{\mathrm{vol}}_n(K))\bigg)^{\frac{n(t-r)}{{t(n+r)}}}. \end{align*} $$
$$ \begin{align*} \mu_{\vec{i}} - as_r(K) &=\omega_{m,k,\vec{i}}^r(K)\\ &=\int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{r}{n+r}}}{\langle x, N(x)\rangle ^{\frac{n(r-1)}{n+r}}}\, d\mu_{\vec{i}} (x) = \int\limits_{\partial K} \left(\frac{H_{n-1}(x)^{\frac{t}{n+t}}}{\langle x, N(x)\rangle ^{\frac{n(t-1)}{n+t}}} \right)^{\frac{r(n+t)}{t(n+r)}} \frac{d\mu_{\vec{i}} (x)}{\langle x, N(x)\rangle ^{\frac{(r-t)n}{(n+r)t}}} \\ &\leq \big(\omega_{m,k,\vec{i}}^t(K)\big)^{\frac{r(n+t)}{t(n+r)}} \big( \omega_{m,k,\vec{i}}^0(K)\big)^{\frac{(t-r)n}{(n+r)t}} \nonumber \\ &= \bigg(\mu_{\vec{i}} - as_t(K)\bigg)^{\frac{r(n+t)}{{t(n+r)}}} \bigg(n(\mu_{\vec{i}}-{\mathrm{vol}}_n(K))\bigg)^{\frac{n(t-r)}{{t(n+r)}}}. \end{align*} $$
The equality characterizations follow from the equality characterization of Hölder’s inequality.
Equality holds in (i) and (ii) if and only if equality holds in Hölder’s inequality which happens if and only if
![]() $\mu _{\vec {i}}$
-almost everywhere on
$\mu _{\vec {i}}$
-almost everywhere on
![]() $\partial K$
. As
$\partial K$
. As
![]() $\partial K$
is
$\partial K$
is
![]() $C^2_+$
,
$C^2_+$
,
![]() $\{ x \in \partial K: \mu _{\vec {i}}(x) =0\} = \emptyset $
and therefore
$\{ x \in \partial K: \mu _{\vec {i}}(x) =0\} = \emptyset $
and therefore
holds for all
![]() $x \in \partial K$
. Thus, we can use the following theorem by Petty [Reference Petty27], which then finishes the proof.
$x \in \partial K$
. Thus, we can use the following theorem by Petty [Reference Petty27], which then finishes the proof.
Theorem 3.3 [Reference Petty27]
Let K be a convex body in
![]() ${\mathbb {R}}^n$
that is
${\mathbb {R}}^n$
that is
![]() $C^2_+$
. K is an ellipsoid if and only if, for all x in
$C^2_+$
. K is an ellipsoid if and only if, for all x in
![]() $\partial K,$
$\partial K,$
where
![]() $c>0$
is a constant.
$c>0$
is a constant.
Theorem 3.4 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin. If
$\mathbb R^n$
with centroid at the origin. If
![]() $r<s<k,$
then
$r<s<k,$
then
Equality holds if and only if K is a ball.
Proof
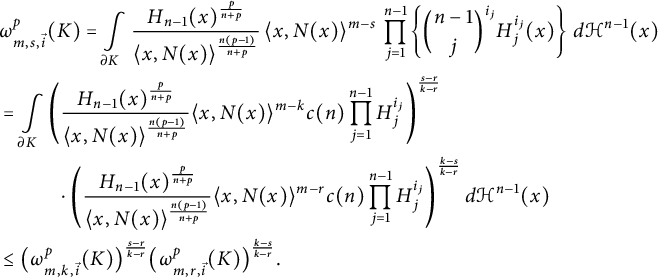 $$ \begin{align} &\omega_{m,s,\vec{i}}^p (K) =\int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-s} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \nonumber \\ &= \int\limits_{\partial K} \left(\frac{H_{n-1}(x)^{\frac{p}{n+p}}}{\langle x, N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \langle x,N(x)\rangle ^{m-k} c(n) \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}\right)^{\frac{s-r}{k-r}}\\ &\hskip 10mm \cdot\left(\frac{H_{n-1}(x)^{\frac{p}{n+p}}}{\langle x, N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \langle x,N(x)\rangle ^{m-r} c(n) \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}\right)^{\frac{k-s}{k-r}} d\mathcal{H}^{n-1}(x) \nonumber\\ &\leq \big(\omega_{m,k,\vec{i}}^p (K) \big)^{\frac{s-r}{k-r}} \big(\omega_{m,r,\vec{i}}^p (K) \big)^{\frac{k-s}{k-r}}. \nonumber \end{align} $$
$$ \begin{align} &\omega_{m,s,\vec{i}}^p (K) =\int\limits_{\partial K}\frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \,\langle x,N(x)\rangle ^{m-s} \, \prod\limits_{j = 1}^{n - 1}\left\{ {n - 1\choose j}^{i_j} H_{j}^{i_j}(x)\right\} \, d\mathcal{H}^{n-1}(x) \nonumber \\ &= \int\limits_{\partial K} \left(\frac{H_{n-1}(x)^{\frac{p}{n+p}}}{\langle x, N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \langle x,N(x)\rangle ^{m-k} c(n) \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}\right)^{\frac{s-r}{k-r}}\\ &\hskip 10mm \cdot\left(\frac{H_{n-1}(x)^{\frac{p}{n+p}}}{\langle x, N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \langle x,N(x)\rangle ^{m-r} c(n) \prod\limits_{j = 1}^{n - 1} H_{j}^{i_j}\right)^{\frac{k-s}{k-r}} d\mathcal{H}^{n-1}(x) \nonumber\\ &\leq \big(\omega_{m,k,\vec{i}}^p (K) \big)^{\frac{s-r}{k-r}} \big(\omega_{m,r,\vec{i}}^p (K) \big)^{\frac{k-s}{k-r}}. \nonumber \end{align} $$
Equality holds if and only if equality holds in Hölder’s inequality which happens if and only if
![]() $\langle x, N(x)\rangle = \mathrm {constant}$
if and only if K is a ball.
$\langle x, N(x)\rangle = \mathrm {constant}$
if and only if K is a ball.
Remark 3.5 When
![]() $\vec {i} = 0$
and
$\vec {i} = 0$
and
![]() $k = 0$
, we recover
$k = 0$
, we recover
![]() $L_p$
affine isoperimetric inequalities of [Reference Werner and Ye39].
$L_p$
affine isoperimetric inequalities of [Reference Werner and Ye39].
We also obtain monotonicity behaviors.
Corollary 3.6 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() ${\mathbb {R}}^n$
with centroid at the origin. Let
${\mathbb {R}}^n$
with centroid at the origin. Let
![]() $p \ne -n$
be a real number.
$p \ne -n$
be a real number.
(i) The function
 $p \rightarrow \left (\frac {\omega _{m, k, \vec {i}}^p (K)}{\omega ^0_{m, k, \vec {i}}(K)}\right )^{\frac {n+p}{p}}$
is increasing in
$p \rightarrow \left (\frac {\omega _{m, k, \vec {i}}^p (K)}{\omega ^0_{m, k, \vec {i}}(K)}\right )^{\frac {n+p}{p}}$
is increasing in
![]() $p \in (-n, \infty )$
and
$p \in (-n, \infty )$
and
![]() $p \in (-\infty , -n)$
.
$p \in (-\infty , -n)$
.
(ii) The function
![]() $p \rightarrow \left (\frac {\omega _{m, k, \vec {i}}^p (K)}{\omega ^0_{m, k, \vec {i}}(K)}\right )^{n+p}$
is decreasing in
$p \rightarrow \left (\frac {\omega _{m, k, \vec {i}}^p (K)}{\omega ^0_{m, k, \vec {i}}(K)}\right )^{n+p}$
is decreasing in
![]() $p \in (-n, \infty )$
and
$p \in (-n, \infty )$
and
![]() $p \in (-\infty , -n)$
.
$p \in (-\infty , -n)$
.
(iii) The inequalities are strict unless K is an ellipsoid.
3.3 Geometric interpretations
We recall several constructions of convex bodies associated with a given convex body K. Namely:
1. Weighted floating bodies [Reference Werner36]
Let K be a convex body in
![]() $ {\mathbb R}^n$
and denote by
$ {\mathbb R}^n$
and denote by
![]() $\lambda $
the Lebesgue measure on
$\lambda $
the Lebesgue measure on
![]() $\mathbb {R}^n$
. Let
$\mathbb {R}^n$
. Let
![]() $s \geq 0,$
and let
$s \geq 0,$
and let
![]() $f:K\rightarrow \mathbb R$
be an integrable function such that
$f:K\rightarrow \mathbb R$
be an integrable function such that
![]() $f>0\ \lambda $
-a.e. The weighted floating body
$f>0\ \lambda $
-a.e. The weighted floating body
![]() $F(K,f,s)$
was defined in [Reference Werner36] (see also [Reference Besau, Ludwig and Werner3–Reference Besau and Werner4]) as the intersection of all closed half-spaces
$F(K,f,s)$
was defined in [Reference Werner36] (see also [Reference Besau, Ludwig and Werner3–Reference Besau and Werner4]) as the intersection of all closed half-spaces
![]() $H^{+}$
whose defining hyperplanes H cut off a set of
$H^{+}$
whose defining hyperplanes H cut off a set of
![]() $(f\, \lambda )$
-measure less than or equal to s from K,
$(f\, \lambda )$
-measure less than or equal to s from K,
It was shown in [Reference Werner36] that
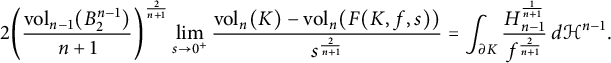 $$ \begin{align*}2 \bigg(\frac{\mbox{vol}_{n-1}(B^{n-1}_2)}{n+1}\bigg)^{\frac{2}{n+1}} \lim_{s \to 0^+} \frac{\mbox{vol}_n(K)-\mbox{vol}_n(F(K,f,s))} {s^{\frac{2}{n+1}}}= \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n+1}}} {f^{\frac{2}{n+1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
$$ \begin{align*}2 \bigg(\frac{\mbox{vol}_{n-1}(B^{n-1}_2)}{n+1}\bigg)^{\frac{2}{n+1}} \lim_{s \to 0^+} \frac{\mbox{vol}_n(K)-\mbox{vol}_n(F(K,f,s))} {s^{\frac{2}{n+1}}}= \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n+1}}} {f^{\frac{2}{n+1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
2. Surface bodies [Reference Schütt and Werner33]
Let K be a convex body, and let
![]() $f:\partial K\rightarrow \mathbb R$
be a nonnegative, integrable function with
$f:\partial K\rightarrow \mathbb R$
be a nonnegative, integrable function with
![]() $\int _{\partial K}f \, \mathcal {H}^{n-1}=1$
. The probability measure
$\int _{\partial K}f \, \mathcal {H}^{n-1}=1$
. The probability measure
![]() $\mathbb P_{f}$
is the measure on
$\mathbb P_{f}$
is the measure on
![]() $\partial K$
with density f. Let
$\partial K$
with density f. Let
![]() $s \geq 0$
. The surface body
$s \geq 0$
. The surface body
![]() $S(K, f,s)$
was defined in [Reference Schütt and Werner33] as the intersection of all the closed half-spaces
$S(K, f,s)$
was defined in [Reference Schütt and Werner33] as the intersection of all the closed half-spaces
![]() $H^{+}$
whose defining hyperplanes H cut off a set of
$H^{+}$
whose defining hyperplanes H cut off a set of
![]() $\mathbb P_{f}$
-measure less than or equal to s from
$\mathbb P_{f}$
-measure less than or equal to s from
![]() $\partial K$
,
$\partial K$
,
It was shown in [Reference Schütt and Werner33] that
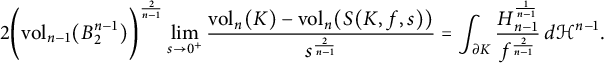 $$ \begin{align*}2 \bigg(\mbox{vol}_{n-1}(B^{n-1}_2)\bigg)^{\frac{2}{n-1}}\lim_{s \to 0^+} \frac{\mathrm{vol}_n(K)-\mathrm{vol}_n(S(K, f,s))} {s^{\frac{2}{n-1}}}= \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n-1}}} {f^{\frac{2}{n-1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
$$ \begin{align*}2 \bigg(\mbox{vol}_{n-1}(B^{n-1}_2)\bigg)^{\frac{2}{n-1}}\lim_{s \to 0^+} \frac{\mathrm{vol}_n(K)-\mathrm{vol}_n(S(K, f,s))} {s^{\frac{2}{n-1}}}= \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n-1}}} {f^{\frac{2}{n-1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
3. Random polytopes [Reference Schütt and Werner32]
A random polytope is the convex hull of finitely many points that are chosen with respect to a probability measure. In [Reference Schütt and Werner32], random polytopes are considered where the points are chosen from
![]() $\partial K$
with respect to
$\partial K$
with respect to
![]() $\mathbb P_{f}$
, where
$\mathbb P_{f}$
, where
![]() $f:\partial K\rightarrow \mathbb R$
is an integrable, nonnegative function with
$f:\partial K\rightarrow \mathbb R$
is an integrable, nonnegative function with
![]() $\int _{\partial K} f \, d\mathcal {H}^{n-1} =1$
and
$\int _{\partial K} f \, d\mathcal {H}^{n-1} =1$
and
![]() $ d \,\mathbb {P}_{f} = f \,d\mathcal {H}^{n-1}$
. Then the expected volume of such a random polytope is
$ d \,\mathbb {P}_{f} = f \,d\mathcal {H}^{n-1}$
. Then the expected volume of such a random polytope is
where
![]() $[x_{1},\dots ,x_{N}]$
is the convex hull of the points
$[x_{1},\dots ,x_{N}]$
is the convex hull of the points
![]() $x_{1},\dots ,x_{N}$
. It was shown in [Reference Schütt and Werner32] that under mild smoothness assumptions on K,
$x_{1},\dots ,x_{N}$
. It was shown in [Reference Schütt and Werner32] that under mild smoothness assumptions on K,
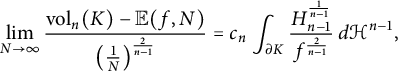 $$ \begin{align*}\lim_{N \to \infty} \frac{\mathrm{vol}_n(K)-\mathbb{E}(f ,N)}{\left(\frac{1}{N}\right)^{\frac{2}{n-1}}}= c_n \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n-1}}} {f^{\frac{2}{n-1}}} \, d\mathcal{H}^{n-1}, \end{align*} $$
$$ \begin{align*}\lim_{N \to \infty} \frac{\mathrm{vol}_n(K)-\mathbb{E}(f ,N)}{\left(\frac{1}{N}\right)^{\frac{2}{n-1}}}= c_n \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n-1}}} {f^{\frac{2}{n-1}}} \, d\mathcal{H}^{n-1}, \end{align*} $$
where
 $c_n=\frac {(n-1)^{\frac {n+1}{n-1}}\Gamma \left (n+1+\tfrac {2}{n-1}\right )} {2(n+1)!(\mathrm {vol}_{n-2}(\partial B_{2}^{n-1}))^{\frac {2}{n-1}}}.$
$c_n=\frac {(n-1)^{\frac {n+1}{n-1}}\Gamma \left (n+1+\tfrac {2}{n-1}\right )} {2(n+1)!(\mathrm {vol}_{n-2}(\partial B_{2}^{n-1}))^{\frac {2}{n-1}}}.$
4. Ulam floating bodies [Reference Huang, Slomka and Werner19]
Given a Borel measure
![]() $\mu $
on
$\mu $
on
![]() ${\mathbb {R}}^{n}$
, the metronoid associated with
${\mathbb {R}}^{n}$
, the metronoid associated with
![]() $\mu $
was introduced by Huang and Slomka [Reference Huang and Slomka18] and is the convex set defined by
$\mu $
was introduced by Huang and Slomka [Reference Huang and Slomka18] and is the convex set defined by
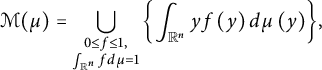 $$\begin{align*}\mathcal{M}(\mu)=\bigcup_{\substack{0\leq f\leq1,\\ \int_{{\mathbb{R}}^{n}}f d{\mu}=1}} \left\{ \int_{{\mathbb{R}}^{n}}yf\left(y\right) d{\mu}\left(y\right)\right\} \!, \end{align*}$$
$$\begin{align*}\mathcal{M}(\mu)=\bigcup_{\substack{0\leq f\leq1,\\ \int_{{\mathbb{R}}^{n}}f d{\mu}=1}} \left\{ \int_{{\mathbb{R}}^{n}}yf\left(y\right) d{\mu}\left(y\right)\right\} \!, \end{align*}$$
where the union is taken over all functions
![]() $0\le f\le 1$
for which
$0\le f\le 1$
for which
![]() $\int _{{\mathbb {R}}^{n}}f d{\mu =1}$
and
$\int _{{\mathbb {R}}^{n}}f d{\mu =1}$
and
![]() $\int _{{\mathbb {R}}^{n}}yf\left (y\right )d{\mu }\left (y\right )$
exists. The metronoid
$\int _{{\mathbb {R}}^{n}}yf\left (y\right )d{\mu }\left (y\right )$
exists. The metronoid
![]() $\mathcal {M}_{\delta }(K)$
is generated by the uniform measure on K with total mass
$\mathcal {M}_{\delta }(K)$
is generated by the uniform measure on K with total mass
![]() $\delta ^{-1}\left |K\right |$
. Namely, let
$\delta ^{-1}\left |K\right |$
. Namely, let
![]() be the characteristic function of K, and let
be the characteristic function of K, and let
![]() $\mu $
be the measure whose density with respect to Lebesgue measure is
$\mu $
be the measure whose density with respect to Lebesgue measure is
![]() . Then
. Then
![]() $\mathcal {M}_{\delta }(K):=\mathcal {M}(\mu )$
. In [Reference Huang, Slomka and Werner19] weighted variations of
$\mathcal {M}_{\delta }(K):=\mathcal {M}(\mu )$
. In [Reference Huang, Slomka and Werner19] weighted variations of
![]() $\mathcal {M}_{\delta }(K)$
were defined where the weight is given by a positive continuous function
$\mathcal {M}_{\delta }(K)$
were defined where the weight is given by a positive continuous function
![]() $f:K\to {\mathbb {R}}$
,
$f:K\to {\mathbb {R}}$
,
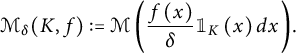
It was shown in [Reference Huang, Slomka and Werner19] that
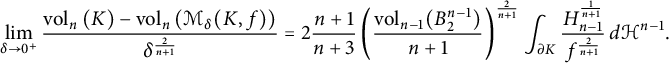 $$ \begin{align*} \lim_{\delta\rightarrow 0^+}\frac{ \mathrm{vol}_{n}\left (K\right)- \mathrm{vol}_{n}\left(\mathcal{M}_{\delta}(K, f)\right)}{\delta^{\frac{2}{n+1}}}= 2\frac{n+1}{n+3}\left(\frac{{\mathrm{vol}}_{n-1}(B_{2}^{n-1})}{n+1}\right)^{\frac{2}{n+1}} \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n+1}}} {f^{\frac{2}{n+1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
$$ \begin{align*} \lim_{\delta\rightarrow 0^+}\frac{ \mathrm{vol}_{n}\left (K\right)- \mathrm{vol}_{n}\left(\mathcal{M}_{\delta}(K, f)\right)}{\delta^{\frac{2}{n+1}}}= 2\frac{n+1}{n+3}\left(\frac{{\mathrm{vol}}_{n-1}(B_{2}^{n-1})}{n+1}\right)^{\frac{2}{n+1}} \int_{\partial K} \frac{H_{n-1}^{\frac{1}{n+1}}} {f^{\frac{2}{n+1}}} \, d\mathcal{H}^{n-1}. \end{align*} $$
This leads to geometric interpretations of the weighted
![]() $L_p$
-affine surface areas in terms of these associated bodies. That is, if we let
$L_p$
-affine surface areas in terms of these associated bodies. That is, if we let
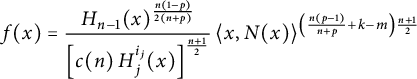 $$ \begin{align*}f(x)= \frac{H_{n-1}(x)^{\frac{n(1-p)}{2(n+p)}}} {\left[c(n)\, H_{j}^{i_j}(x)\right]^{\frac{n+1}{2}}} \,\langle x,N(x)\rangle ^{\left(\frac{n(p-1)}{n+p} +k-m\right) \frac{n+1}{2} } \end{align*} $$
$$ \begin{align*}f(x)= \frac{H_{n-1}(x)^{\frac{n(1-p)}{2(n+p)}}} {\left[c(n)\, H_{j}^{i_j}(x)\right]^{\frac{n+1}{2}}} \,\langle x,N(x)\rangle ^{\left(\frac{n(p-1)}{n+p} +k-m\right) \frac{n+1}{2} } \end{align*} $$
in the case of weighted floating bodies and Ulam floating bodies, and
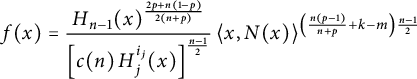 $$ \begin{align*}f(x)= \frac{H_{n-1}(x)^{\frac{2p+n(1-p)}{2(n+p)}}} {\left[c(n)\, H_{j}^{i_j}(x)\right]^{\frac{n-1}{2}}} \,\langle x,N(x)\rangle ^{\left(\frac{n(p-1)}{n+p} +k-m\right) \frac{n-1}{2} } \end{align*} $$
$$ \begin{align*}f(x)= \frac{H_{n-1}(x)^{\frac{2p+n(1-p)}{2(n+p)}}} {\left[c(n)\, H_{j}^{i_j}(x)\right]^{\frac{n-1}{2}}} \,\langle x,N(x)\rangle ^{\left(\frac{n(p-1)}{n+p} +k-m\right) \frac{n-1}{2} } \end{align*} $$
in the case of surface bodies and random polytopes, respectively, and denote by
![]() $K_{f,s}$
the corresponding associated body, i.e.,
$K_{f,s}$
the corresponding associated body, i.e.,
then, with the properly adjusted constant
![]() $c_n$
, we get the following proposition.
$c_n$
, we get the following proposition.
Proposition 3.7 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() ${\mathbb {R}}^n$
with centroid at the origin. Let
${\mathbb {R}}^n$
with centroid at the origin. Let
![]() $p \ne -n$
be a real number.
$p \ne -n$
be a real number.
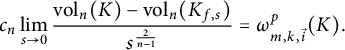 $$ \begin{align*} c_n \lim_{s \to 0} \frac{\mathrm{vol}_n(K)-\mathrm{vol}_n(K_{f,s})} {s^{\frac{2}{n-1}}}= \omega_{m,k,\vec{i}}^p (K). \end{align*} $$
$$ \begin{align*} c_n \lim_{s \to 0} \frac{\mathrm{vol}_n(K)-\mathrm{vol}_n(K_{f,s})} {s^{\frac{2}{n-1}}}= \omega_{m,k,\vec{i}}^p (K). \end{align*} $$
3.4 Asymptotics for the weighted
 $L_p$
-affine surface areas
$L_p$
-affine surface areas
Let
![]() $(X, \mu )$
be a measure space, and let
$(X, \mu )$
be a measure space, and let
![]() $dP = p d\mu $
and
$dP = p d\mu $
and
![]() $Q = q d\mu $
be measures in X that are absolutely continuous with respect to the measure
$Q = q d\mu $
be measures in X that are absolutely continuous with respect to the measure
![]() $\mu $
. The Kullback–Leibler divergence or relative entropy from P to Q is defined as in [Reference Cover and Thomas11]
$\mu $
. The Kullback–Leibler divergence or relative entropy from P to Q is defined as in [Reference Cover and Thomas11]
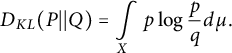 $$ \begin{align} D_{KL}(P||Q) = \int\limits_X p \log{\frac pq} d\mu. \end{align} $$
$$ \begin{align} D_{KL}(P||Q) = \int\limits_X p \log{\frac pq} d\mu. \end{align} $$
The information inequality (also called Gibb’s inequality) [Reference Cover and Thomas11] holds for the Kullback–Leibler divergence. Let P and Q be as above, then
with equality if and only if
![]() $P=Q$
.
$P=Q$
.
We will apply this when
![]() $(X, \mu ) = (\partial K, \mu _{\vec {i}})$
, where K is
$(X, \mu ) = (\partial K, \mu _{\vec {i}})$
, where K is
![]() $C^2_+$
and densities p and q with respect to
$C^2_+$
and densities p and q with respect to
![]() $\mu _{\vec {i}}$
given by
$\mu _{\vec {i}}$
given by
We let
Recall that classical cone measure
![]() $cm_K$
on
$cm_K$
on
![]() $\partial K$
is defined as follows: for every measurable set
$\partial K$
is defined as follows: for every measurable set
![]() $A \subseteq \partial K,$
$A \subseteq \partial K,$
It is wellknown (see, e.g., [Reference Paouris and Werner26] for a proof) that the measures
![]() $\frac {H_{n-1}}{\langle x,N(x)\rangle ^n}\mathcal {H}^{n-1}$
and
$\frac {H_{n-1}}{\langle x,N(x)\rangle ^n}\mathcal {H}^{n-1}$
and
![]() $\langle x,N(x)\rangle \mathcal {H}^{n-1}$
are the cone measures of K and
$\langle x,N(x)\rangle \mathcal {H}^{n-1}$
are the cone measures of K and
![]() $K^\circ $
,
$K^\circ $
,
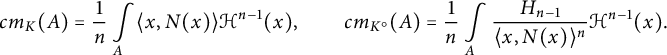 $$ \begin{align*} cm_K(A) = \frac1n \int\limits_{A} \langle x,N(x)\rangle \mathcal{H}^{n-1}(x), \qquad cm_{K^\circ}(A) = \frac1n \int\limits_{A} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \mathcal{H}^{n-1}(x). \end{align*} $$
$$ \begin{align*} cm_K(A) = \frac1n \int\limits_{A} \langle x,N(x)\rangle \mathcal{H}^{n-1}(x), \qquad cm_{K^\circ}(A) = \frac1n \int\limits_{A} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \mathcal{H}^{n-1}(x). \end{align*} $$
The interpretation of
![]() $cm_{K^\circ }$
as the “cone measure of
$cm_{K^\circ }$
as the “cone measure of
![]() $K^\circ $
” is via the Gauss map on
$K^\circ $
” is via the Gauss map on
![]() $K^\circ $
,
$K^\circ $
,
![]() $N_{K^\circ }: \partial K^\circ \rightarrow S^{n-1}, \ x \longmapsto N_{K^\circ }(x)$
and the inverse of the Gauss map on
$N_{K^\circ }: \partial K^\circ \rightarrow S^{n-1}, \ x \longmapsto N_{K^\circ }(x)$
and the inverse of the Gauss map on
![]() $K N_{K}: \partial K \rightarrow S^{n-1}, \ x \longmapsto N_{K}(x)$
,
$K N_{K}: \partial K \rightarrow S^{n-1}, \ x \longmapsto N_{K}(x)$
,
where we use
![]() $N_K(x)$
to emphasize that it is the normal vector of a body K at
$N_K(x)$
to emphasize that it is the normal vector of a body K at
![]() $x \in \partial K$
.
$x \in \partial K$
.
We now define the weighted cone measures
![]() $\mu _{\vec {i}} -cm_K$
of K and
$\mu _{\vec {i}} -cm_K$
of K and
![]() $\mu _{\vec {i}} -cm_{K^\circ }$
of
$\mu _{\vec {i}} -cm_{K^\circ }$
of
![]() $K^\circ $
by
$K^\circ $
by
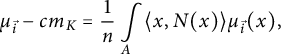 $$ \begin{align} \mu_{\vec{i}} -cm_K = \frac1n \int\limits_{A} \langle x,N(x)\rangle \mu_{\vec{i}}(x), \end{align} $$
$$ \begin{align} \mu_{\vec{i}} -cm_K = \frac1n \int\limits_{A} \langle x,N(x)\rangle \mu_{\vec{i}}(x), \end{align} $$
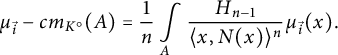 $$ \begin{align} \mu_{\vec{i}} -cm_{K^\circ} (A )= \frac1n \int\limits_{A} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \mu_{\vec{i}}(x). \end{align} $$
$$ \begin{align} \mu_{\vec{i}} -cm_{K^\circ} (A )= \frac1n \int\limits_{A} \frac{H_{n-1}}{\langle x,N(x)\rangle^n} \mu_{\vec{i}}(x). \end{align} $$
We show that the limits of the weighted
![]() $L_p$
affine surface areas are entropy powers.
$L_p$
affine surface areas are entropy powers.
Theorem 3.8 Let K be a
![]() $C^2_+$
convex body in
$C^2_+$
convex body in
![]() $\mathbb R^n$
with centroid at the origin.
$\mathbb R^n$
with centroid at the origin.
(i)
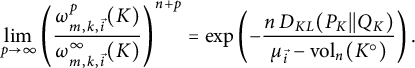 $$ \begin{align*} \lim\limits_{p \rightarrow \infty} \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_K||Q_K)}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
$$ \begin{align*} \lim\limits_{p \rightarrow \infty} \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_K||Q_K)}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
(ii)
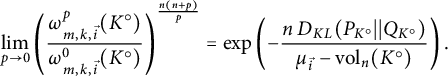 $$ \begin{align*} \lim\limits_{p \rightarrow 0} \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_{K^\circ}||Q_{K^\circ})}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
$$ \begin{align*} \lim\limits_{p \rightarrow 0} \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} = \mathrm{exp} \left(-\frac{n \, D_{KL} (P_{K^\circ}||Q_{K^\circ})}{\mu_{\vec{i}} - {\mathrm{vol}}_n(K^\circ)}\right). \end{align*} $$
Proof (i) We use L’Hospital’s rule
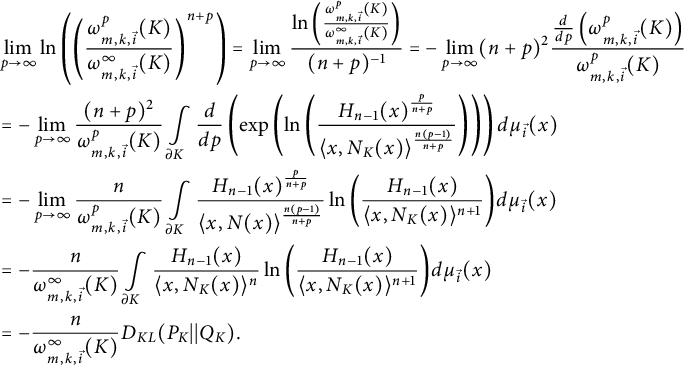 $$ \begin{align*} &\lim\limits_{p \rightarrow \infty} \ln \left(\left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} \right) = \lim\limits_{p \rightarrow \infty} \frac{\ln \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)} \right)}{(n+p)^{-1}} = - \lim\limits_{p \rightarrow \infty} (n+p)^2 \frac{\frac{d}{dp} \left(\omega_{m, k, \vec{i}}^p (K)\right) }{\omega_{m, k, \vec{i}}^p (K)} \\ &= -\lim\limits_{p \rightarrow \infty} \frac{(n+p)^2}{\omega_{m, k, \vec{i}}^p (K)} \int\limits_{\partial K} \frac{d}{dp} \left( \mathrm{exp} \left( \ln \left( \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_K(x)\rangle ^{\frac{n(p-1)}{n+p}}} \right) \right) \right) d\mu_{\vec{i}} (x)\\ &= -\lim\limits_{p \rightarrow \infty} \frac{n}{\omega_{m, k, \vec{i}}^p (K)} \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_K(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega_{m, k, \vec{i}}^\infty (K)} \int\limits_{\partial K} \frac{H_{n-1}(x)} {\langle x,N_K(x)\rangle ^n} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_K(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega_{m, k, \vec{i}}^\infty (K)} D_{KL}(P_K||Q_K). \end{align*} $$
$$ \begin{align*} &\lim\limits_{p \rightarrow \infty} \ln \left(\left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)}\right)^{n+p} \right) = \lim\limits_{p \rightarrow \infty} \frac{\ln \left(\frac{\omega_{m, k, \vec{i}}^p (K)}{\omega^\infty_{m, k, \vec{i}}(K)} \right)}{(n+p)^{-1}} = - \lim\limits_{p \rightarrow \infty} (n+p)^2 \frac{\frac{d}{dp} \left(\omega_{m, k, \vec{i}}^p (K)\right) }{\omega_{m, k, \vec{i}}^p (K)} \\ &= -\lim\limits_{p \rightarrow \infty} \frac{(n+p)^2}{\omega_{m, k, \vec{i}}^p (K)} \int\limits_{\partial K} \frac{d}{dp} \left( \mathrm{exp} \left( \ln \left( \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_K(x)\rangle ^{\frac{n(p-1)}{n+p}}} \right) \right) \right) d\mu_{\vec{i}} (x)\\ &= -\lim\limits_{p \rightarrow \infty} \frac{n}{\omega_{m, k, \vec{i}}^p (K)} \int\limits_{\partial K} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N(x)\rangle ^{\frac{n(p-1)}{n+p}}} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_K(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega_{m, k, \vec{i}}^\infty (K)} \int\limits_{\partial K} \frac{H_{n-1}(x)} {\langle x,N_K(x)\rangle ^n} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_K(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega_{m, k, \vec{i}}^\infty (K)} D_{KL}(P_K||Q_K). \end{align*} $$
(ii) We use L’Hospital’s rule
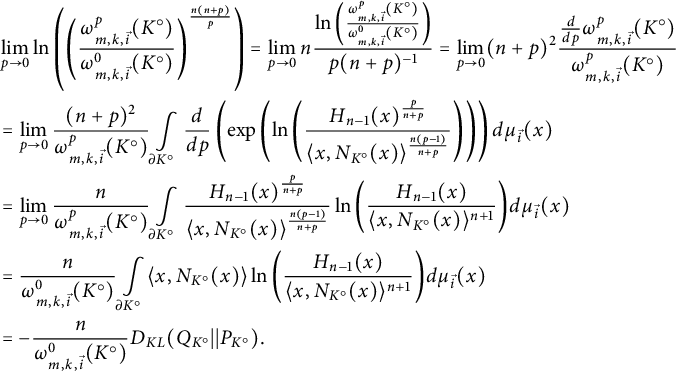 $$ \begin{align*} &\lim\limits_{p \rightarrow 0} \ln \left( \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} \right) = \lim\limits_{p \rightarrow 0} n \frac{\ln \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)} \right)}{p(n+p)^{-1}} = \lim\limits_{p \rightarrow 0} (n+p)^2 \frac{\frac{d}{dp}\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^p_{m, k, \vec{i}}(K^\circ)}\\ &= \lim\limits_{p \rightarrow 0} \frac{(n+p)^2}{\omega^p_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \frac{d}{dp} \left( \mathrm{exp} \left( \ln \left( \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_{K^\circ}(x)\rangle ^{\frac{n(p-1)}{n+p}}} \right) \right) \right) d\mu_{\vec{i}} (x)\\ &= \lim\limits_{p \rightarrow 0} \frac{n}{\omega^p_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_{K^\circ}(x)\rangle ^{\frac{n(p-1)}{n+p}}} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_{K^\circ}(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= \frac{n}{\omega^0_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \langle x,N_{K^\circ}(x)\rangle \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_{K^\circ}(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega^0_{m, k, \vec{i}}(K^\circ)} D_{KL}(Q_{K^\circ}||P_{K^\circ}).\\[-34pt] \end{align*} $$
$$ \begin{align*} &\lim\limits_{p \rightarrow 0} \ln \left( \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)}\right)^{\frac{n(n+p)}p} \right) = \lim\limits_{p \rightarrow 0} n \frac{\ln \left(\frac{\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^0_{m, k, \vec{i}}(K^\circ)} \right)}{p(n+p)^{-1}} = \lim\limits_{p \rightarrow 0} (n+p)^2 \frac{\frac{d}{dp}\omega_{m, k, \vec{i}}^p (K^\circ)}{\omega^p_{m, k, \vec{i}}(K^\circ)}\\ &= \lim\limits_{p \rightarrow 0} \frac{(n+p)^2}{\omega^p_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \frac{d}{dp} \left( \mathrm{exp} \left( \ln \left( \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_{K^\circ}(x)\rangle ^{\frac{n(p-1)}{n+p}}} \right) \right) \right) d\mu_{\vec{i}} (x)\\ &= \lim\limits_{p \rightarrow 0} \frac{n}{\omega^p_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \frac{H_{n-1}(x)^{\frac{p}{n+p}}} {\langle x,N_{K^\circ}(x)\rangle ^{\frac{n(p-1)}{n+p}}} \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_{K^\circ}(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= \frac{n}{\omega^0_{m, k, \vec{i}}(K^\circ)} \int\limits_{\partial K^\circ} \langle x,N_{K^\circ}(x)\rangle \ln{\left( \frac{H_{n-1}(x)}{\langle x,N_{K^\circ}(x)\rangle^{n+1}}\right)} d\mu_{\vec{i}} (x)\\ &= - \frac{n}{\omega^0_{m, k, \vec{i}}(K^\circ)} D_{KL}(Q_{K^\circ}||P_{K^\circ}).\\[-34pt] \end{align*} $$
4 f-divergence
The results in the previous section lead naturally to consider more general f-divergences than just the Kullback–Leibler divergence.
4.1 Background on f-divergence
In information theory, probability theory and statistics, an f-divergence is a functional that measures the difference between two (probability) distributions. This notion was introduced by Csiszár [Reference Csiszár12], and independently Morimoto [Reference Morimoto25] and Ali and Silvery [Reference Ali and Silvey2].
Let
![]() $(X, \mu )$
be a measure space, and let
$(X, \mu )$
be a measure space, and let
![]() $P=p \mu $
and
$P=p \mu $
and
![]() $Q=q \mu $
be (probability) measures on X that are absolutely continuous with respect to the measure
$Q=q \mu $
be (probability) measures on X that are absolutely continuous with respect to the measure
![]() $\mu $
. Let
$\mu $
. Let
![]() $f: (0, \infty ) \rightarrow \mathbb {R}$
be a convex or a concave function. The
$f: (0, \infty ) \rightarrow \mathbb {R}$
be a convex or a concave function. The
![]() $*$
-adjoint function
$*$
-adjoint function
![]() $f^*:(0, \infty ) \rightarrow \mathbb {R}$
of f is defined by
$f^*:(0, \infty ) \rightarrow \mathbb {R}$
of f is defined by
It is obvious that
![]() $(f^*)^*=f$
and that
$(f^*)^*=f$
and that
![]() $f^*$
is again convex, if f is convex, respectively, concave, if f is concave. Then the f-divergence
$f^*$
is again convex, if f is convex, respectively, concave, if f is concave. Then the f-divergence
![]() $D_f(P,Q)$
of the measures P and Q is defined by
$D_f(P,Q)$
of the measures P and Q is defined by
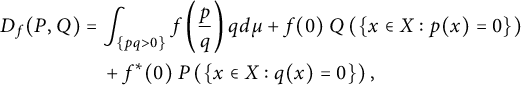 $$ \begin{align} D_f(P,Q)&= \int_{\{pq>0\} }f\left(\frac{p}{q} \right) q d\mu + f(0)\ Q\left(\{x\in X: p(x) =0\}\right)\nonumber \\ &\quad+ f^*(0) \ P\left(\{x\in X: q(x) =0\}\right), \end{align} $$
$$ \begin{align} D_f(P,Q)&= \int_{\{pq>0\} }f\left(\frac{p}{q} \right) q d\mu + f(0)\ Q\left(\{x\in X: p(x) =0\}\right)\nonumber \\ &\quad+ f^*(0) \ P\left(\{x\in X: q(x) =0\}\right), \end{align} $$
provided the expressions exist. Here,
We make the convention that
![]() $0 \cdot \infty =0$
.
$0 \cdot \infty =0$
.
Please note that
With (4.3) and as
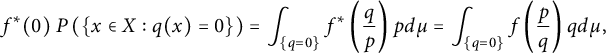 $$ \begin{align*}f^*(0) \ P\left(\{x\in X: q(x) =0\}\right) = \int _{\{q=0\}} f^*\left(\frac{q}{p} \right) p d\mu = \int _{\{q=0\}} f\left(\frac{p}{q} \right) q d\mu,\end{align*} $$
$$ \begin{align*}f^*(0) \ P\left(\{x\in X: q(x) =0\}\right) = \int _{\{q=0\}} f^*\left(\frac{q}{p} \right) p d\mu = \int _{\{q=0\}} f\left(\frac{p}{q} \right) q d\mu,\end{align*} $$
we can write in short
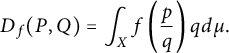 $$ \begin{align} D_f(P,Q)= \int_{X} f\left(\frac{p}{q} \right) q d\mu. \end{align} $$
$$ \begin{align} D_f(P,Q)= \int_{X} f\left(\frac{p}{q} \right) q d\mu. \end{align} $$
Examples of f-divergences are as follows:
1. For
![]() $f(t) = t \ln t$
(with
$f(t) = t \ln t$
(with
![]() $*$
-adjoint function
$*$
-adjoint function
![]() $f^*(t) = - \ln t$
), the f-divergence is Kullback–Leibler divergence or relative entropy from P to Q (see [Reference Cover and Thomas11])
$f^*(t) = - \ln t$
), the f-divergence is Kullback–Leibler divergence or relative entropy from P to Q (see [Reference Cover and Thomas11])
2. For the convex or concave functions
![]() $f(t) = t^\alpha ,$
we obtain the Hellinger integrals (e.g., [Reference Liese and Vajda20])
$f(t) = t^\alpha ,$
we obtain the Hellinger integrals (e.g., [Reference Liese and Vajda20])
Those are related to the Rényi divergence of order
![]() $\alpha $
,
$\alpha $
,
![]() $\alpha \neq 1$
, introduced by Rényi [Reference Rényi28] (for
$\alpha \neq 1$
, introduced by Rényi [Reference Rényi28] (for
![]() $\alpha>0$
) as
$\alpha>0$
) as
The case
![]() $\alpha =1$
is the relative entropy
$\alpha =1$
is the relative entropy
![]() $ D_{KL}(P\|Q)$
.
$ D_{KL}(P\|Q)$
.
More on f-divergence can be found in, e.g., [Reference Caglar, Kolesnikov and Werner7–Reference Caglar and Werner9, Reference Liese and Vajda20, Reference Werner37, Reference Werner38, Reference Werner and Ye40].
4.2 f-divergence for the
 $\mu _{\vec {i}}$
-measure
$\mu _{\vec {i}}$
-measure
In [Reference Werner38], f-divergence with respect to the surface area measure
![]() $\mu _K$
was introduced for a convex body K in
$\mu _K$
was introduced for a convex body K in
![]() $\mathbb {R}^n$
with
$\mathbb {R}^n$
with
![]() $0$
in its interior. We now introduce similarly f-divergence with respect to the measure
$0$
in its interior. We now introduce similarly f-divergence with respect to the measure
![]() $\mu _{\vec {i}}$
.
$\mu _{\vec {i}}$
.
Definition 4.1 Let
![]() $f: (0, \infty ) \rightarrow \mathbb {R}$
be a convex or concave function. Let
$f: (0, \infty ) \rightarrow \mathbb {R}$
be a convex or concave function. Let
![]() $p_K$
and
$p_K$
and
![]() $q_K$
be as in (3.5). Then the f-divergence
$q_K$
be as in (3.5). Then the f-divergence
![]() $D_f \left (P_K, Q_K \right )$
of a convex body K in
$D_f \left (P_K, Q_K \right )$
of a convex body K in
![]() $\mathbb {R}^n$
with respect to the
$\mathbb {R}^n$
with respect to the
![]() $\mu _{\vec {i}}$
-measure is
$\mu _{\vec {i}}$
-measure is
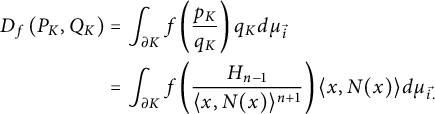 $$ \begin{align*} D_f \left(P_K, Q_K \right)&= \int_{\partial K } f \left(\frac{p_K}{q_K}\right) q_K d \mu_{\vec{i}}\\ &=\int_{\partial K } f \left( \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \right) \langle x,N(x)\rangle d \mu_{\vec{i.}} \end{align*} $$
$$ \begin{align*} D_f \left(P_K, Q_K \right)&= \int_{\partial K } f \left(\frac{p_K}{q_K}\right) q_K d \mu_{\vec{i}}\\ &=\int_{\partial K } f \left( \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \right) \langle x,N(x)\rangle d \mu_{\vec{i.}} \end{align*} $$
In particular, for
![]() $f(t)=t \log t,$
we recover the above Kullback–Leibler divergences of Section 3.4 and for
$f(t)=t \log t,$
we recover the above Kullback–Leibler divergences of Section 3.4 and for
![]() $f(t) = t^{\frac {p}{n+p}}$
, we obtain the weighted
$f(t) = t^{\frac {p}{n+p}}$
, we obtain the weighted
![]() $L_p$
-affine surface areas.
$L_p$
-affine surface areas.
Remarks (i) By (4.4),
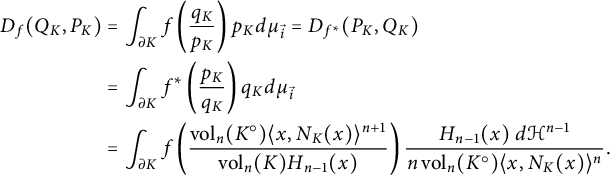 $$ \begin{align} D_f(Q_K,P_K)&= \int _{\partial K} f\left(\frac{q_K}{p_K}\right) p_K d\mu_{\vec{i}} = D_{f^*}(P_K, Q_K) \nonumber \\ &= \int _{\partial K} f^*\left(\frac{p_K}{q_K}\right) q_K d\mu_{\vec{i}} \\ &= \int _{\partial K} f\left(\frac{ {\mathrm{vol}}_n( K^\circ )\langle x, N_K(x) \rangle ^{n+1}}{{\mathrm{vol}}_n(K) H_{n-1} (x)} \right)\frac{H_{n-1}(x)\ d\mathcal{H}^{n-1}} {n\, {\mathrm{vol}}_n(K^\circ) \langle x, N_K(x) \rangle ^{n}}. \nonumber \end{align} $$
$$ \begin{align} D_f(Q_K,P_K)&= \int _{\partial K} f\left(\frac{q_K}{p_K}\right) p_K d\mu_{\vec{i}} = D_{f^*}(P_K, Q_K) \nonumber \\ &= \int _{\partial K} f^*\left(\frac{p_K}{q_K}\right) q_K d\mu_{\vec{i}} \\ &= \int _{\partial K} f\left(\frac{ {\mathrm{vol}}_n( K^\circ )\langle x, N_K(x) \rangle ^{n+1}}{{\mathrm{vol}}_n(K) H_{n-1} (x)} \right)\frac{H_{n-1}(x)\ d\mathcal{H}^{n-1}} {n\, {\mathrm{vol}}_n(K^\circ) \langle x, N_K(x) \rangle ^{n}}. \nonumber \end{align} $$
(ii) f-divergences can also be expressed as integrals over
![]() $S^{n-1}$
,
$S^{n-1}$
,
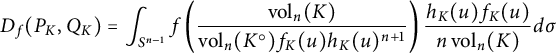 $$ \begin{align} D_f(P_K, Q_K)&= \int _{S^{n-1}} f\left(\frac{{\mathrm{vol}}_n(K) } {{\mathrm{vol}}_n(K^\circ) f_K(u) h_K(u) ^{n+1}}\right)\frac{ h_K(u)f_K(u)}{n\, {\mathrm{vol}}_n(K)} d\sigma \end{align} $$
$$ \begin{align} D_f(P_K, Q_K)&= \int _{S^{n-1}} f\left(\frac{{\mathrm{vol}}_n(K) } {{\mathrm{vol}}_n(K^\circ) f_K(u) h_K(u) ^{n+1}}\right)\frac{ h_K(u)f_K(u)}{n\, {\mathrm{vol}}_n(K)} d\sigma \end{align} $$
and
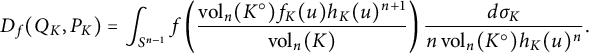 $$ \begin{align} D_f(Q_K,P_K)&= \int _{ S^{n-1}} f\left(\frac{ {\mathrm{vol}}_n(K^\circ) f_K(u) h_K(u) ^{n+1}}{{\mathrm{vol}}_n(K) } \right)\frac{ d\sigma_K} {n\, {\mathrm{vol}}_n(K^\circ )h_K(u)^{n}}. \end{align} $$
$$ \begin{align} D_f(Q_K,P_K)&= \int _{ S^{n-1}} f\left(\frac{ {\mathrm{vol}}_n(K^\circ) f_K(u) h_K(u) ^{n+1}}{{\mathrm{vol}}_n(K) } \right)\frac{ d\sigma_K} {n\, {\mathrm{vol}}_n(K^\circ )h_K(u)^{n}}. \end{align} $$
(iii) Similar to (4.10) and (4.11), one can define mixed f-divergences for n convex bodies in
![]() $\mathbb {R}^n$
. We will not treat those here but will concentrate on f-divergence for one convex body. We also refer to [Reference Ye41], where they have been investigated for functions in
$\mathbb {R}^n$
. We will not treat those here but will concentrate on f-divergence for one convex body. We also refer to [Reference Ye41], where they have been investigated for functions in
![]() $Conv(0,\infty )$
.
$Conv(0,\infty )$
.
Proposition 4.1 Let
![]() $f: (0, \infty ) \rightarrow \mathbb {R}$
be a concave function. Then
$f: (0, \infty ) \rightarrow \mathbb {R}$
be a concave function. Then
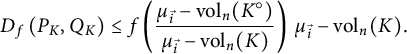 $$ \begin{align*} D_f \left(P_K, Q_K \right)\leq f\left(\frac{\mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ}) }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K) } \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
$$ \begin{align*} D_f \left(P_K, Q_K \right)\leq f\left(\frac{\mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ}) }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K) } \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
If f is convex, the inequality is reversed. If f is linear, equality holds in Proposition 4.1. If f is not linear, equality holds iff K is an ellipsoid.
Proof Let
![]() $f: (0, \infty ) \rightarrow \mathbb {R}$
be a concave function. By Jensen’s inequality,
$f: (0, \infty ) \rightarrow \mathbb {R}$
be a concave function. By Jensen’s inequality,
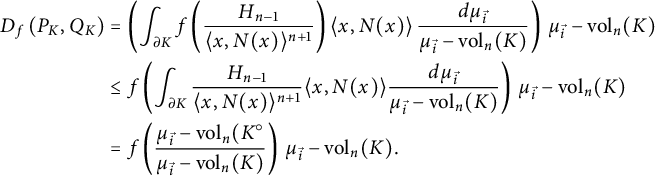 $$ \begin{align*} D_f \left(P_K, Q_K \right) &= \left(\int_{\partial K } f \left( \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \right) \langle x,N(x)\rangle \, \frac{d \mu_{\vec{i}} }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)} \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K)\\ &\leq f\left(\int_{\partial K } \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \langle x,N(x) \rangle \frac{ d \mu_{\vec{i}}} { \mu_{\vec{i}}-{\mathrm{vol}}_n(K)} \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K) \\&= f\left(\frac{\mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ} }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K) } \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
$$ \begin{align*} D_f \left(P_K, Q_K \right) &= \left(\int_{\partial K } f \left( \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \right) \langle x,N(x)\rangle \, \frac{d \mu_{\vec{i}} }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K)} \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K)\\ &\leq f\left(\int_{\partial K } \frac{H_{n-1}}{\langle x,N(x)\rangle^{n+1}} \langle x,N(x) \rangle \frac{ d \mu_{\vec{i}}} { \mu_{\vec{i}}-{\mathrm{vol}}_n(K)} \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K) \\&= f\left(\frac{\mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ} }{\mu_{\vec{i}}-{\mathrm{vol}}_n(K) } \right) \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
Equality holds in Jensen’s inequality iff either f is linear or
![]() $\frac {p_K}{q_K}$
is constant. Indeed, if
$\frac {p_K}{q_K}$
is constant. Indeed, if
![]() $f(t) = at +b$
, then
$f(t) = at +b$
, then
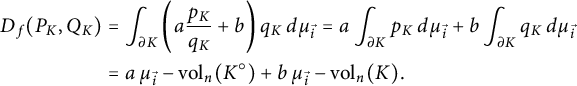 $$ \begin{align*} D_f(P_K, Q_K)&= \int _{\partial K } \left(a \frac{p_K}{q_K} +b \right) q_K \, d \mu_{\vec{i}} = a \int _{\partial K } p_K \, d \mu_{\vec{i}} + b \int _{\partial K } q_K \, d \mu_{\vec{i}} \\ &= a \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ}) +b \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
$$ \begin{align*} D_f(P_K, Q_K)&= \int _{\partial K } \left(a \frac{p_K}{q_K} +b \right) q_K \, d \mu_{\vec{i}} = a \int _{\partial K } p_K \, d \mu_{\vec{i}} + b \int _{\partial K } q_K \, d \mu_{\vec{i}} \\ &= a \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K^{\circ}) +b \, \mu_{\vec{i}}-{\mathrm{vol}}_n(K). \end{align*} $$
If f is not linear, equality holds iff
![]() $\frac {p_K}{q_K}=c$
, where c is a constant. By the above quoted Theorem 3.3 of Petty, this holds iff K is an ellipsoid. Note that the constant c is different from
$\frac {p_K}{q_K}=c$
, where c is a constant. By the above quoted Theorem 3.3 of Petty, this holds iff K is an ellipsoid. Note that the constant c is different from
![]() $0$
, as we assume that K is
$0$
, as we assume that K is
![]() $C^2_+$
.
$C^2_+$
.
Now we show that
![]() $D_f({P}_K,{Q}_K)$
are valuations, i.e., for convex bodies K and L such that
$D_f({P}_K,{Q}_K)$
are valuations, i.e., for convex bodies K and L such that
![]() $K \cup L $
is convex,
$K \cup L $
is convex,
Proposition 4.2 Let K be a convex body in
![]() ${\mathbb {R}}^n$
with the origin in its interior, and let
${\mathbb {R}}^n$
with the origin in its interior, and let
![]() $f:~(0, \infty ) \rightarrow \mathbb {R}$
be a convex function. Then
$f:~(0, \infty ) \rightarrow \mathbb {R}$
be a convex function. Then
![]() $D_f(P_K,Q_K)$
are valuations.
$D_f(P_K,Q_K)$
are valuations.
Proof To prove (4.12), we proceed as in Schütt [Reference Schütt31]. For completeness, we include the argument. We decompose
 $$ \begin{align*}\partial (K \cup L) &= (\partial K \cap \partial L) \cup (\partial K \cap L^c) \cup ( K^c \cap \partial L),\\ \partial (K \cap L) &= (\partial K \cap \partial L) \cup (\partial K \cap \text{int} L) \cup (\text{int} K \cap \partial L),\\ \partial K &= (\partial K \cap \partial L) \cup (\partial K \cap L^c) \cup (\partial K \cap \text{int} L),\\ \partial L &= (\partial K \cap \partial L) \cup (\partial K^c \cap \partial L) \cup (\text{int} K \cap \partial L), \end{align*} $$
$$ \begin{align*}\partial (K \cup L) &= (\partial K \cap \partial L) \cup (\partial K \cap L^c) \cup ( K^c \cap \partial L),\\ \partial (K \cap L) &= (\partial K \cap \partial L) \cup (\partial K \cap \text{int} L) \cup (\text{int} K \cap \partial L),\\ \partial K &= (\partial K \cap \partial L) \cup (\partial K \cap L^c) \cup (\partial K \cap \text{int} L),\\ \partial L &= (\partial K \cap \partial L) \cup (\partial K^c \cap \partial L) \cup (\text{int} K \cap \partial L), \end{align*} $$
where all unions on the right-hand side are disjoint. Note that for x such that the curvatures
![]() $\kappa _K(x)$
,
$\kappa _K(x)$
,
![]() $\kappa _L(x)$
,
$\kappa _L(x)$
,
![]() $\kappa _{K\cup L} (x),$
and
$\kappa _{K\cup L} (x),$
and
![]() $\kappa _{K\cap L} (x)$
exist,
$\kappa _{K\cap L} (x)$
exist,
and
To prove (4.12), we split the involved integral using the above decompositions (4.13) and (4.14).