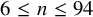1 Introduction
For
![]() $n\geq 2$
, let
$n\geq 2$
, let
![]() $N_n(X)$
denote the number of isomorphism classes of number fields of degree n having absolute discriminant less than X. In 1995, Schmidt [Reference Schmidt14] proved the following upper bound on
$N_n(X)$
denote the number of isomorphism classes of number fields of degree n having absolute discriminant less than X. In 1995, Schmidt [Reference Schmidt14] proved the following upper bound on
![]() $N_n(X)$
:
$N_n(X)$
:
Theorem 1.1 (Schmidt)
We have
A folklore conjecture predicts that
![]() $N_n(X)\asymp X$
. This conjecture is elementary for
$N_n(X)\asymp X$
. This conjecture is elementary for
![]() $n=2$
; for
$n=2$
; for
![]() $n=3$
, it was proven by Davenport and Heilbronn [Reference Davenport and Heilbronn11] and for
$n=3$
, it was proven by Davenport and Heilbronn [Reference Davenport and Heilbronn11] and for
![]() $n=4, 5$
, by the first-named author [Reference Bhargava2, Reference Bhargava3]; these works, in fact, determine asymptotics for
$n=4, 5$
, by the first-named author [Reference Bhargava2, Reference Bhargava3]; these works, in fact, determine asymptotics for
![]() $N_n(X)$
as
$N_n(X)$
as
![]() $X\to \infty $
.
$X\to \infty $
.
For large n, the exponent of X in (1.1) was substantially improved by Ellenberg–Venkatesh [Reference Ellenberg and Venkatesh12], Couveignes [Reference Couveignes10] and Lemke Oliver–Thorne [Reference Lemke Oliver and Thorne13], to
![]() $O(\exp (c\sqrt {\log n}))$
,
$O(\exp (c\sqrt {\log n}))$
,
![]() $O(\log ^3 n)$
and
$O(\log ^3 n)$
and
![]() $O(\log ^2 n)$
, respectively. In particular, in view of the implied O-constants, the latter work of Lemke Oliver and Thorne improved Schmidt’s bound for all
$O(\log ^2 n)$
, respectively. In particular, in view of the implied O-constants, the latter work of Lemke Oliver and Thorne improved Schmidt’s bound for all
![]() $n\geq 95$
, while Schmidt’s bound has remained the best known for
$n\geq 95$
, while Schmidt’s bound has remained the best known for
![]() $6\leq n\leq 94$
.
$6\leq n\leq 94$
.
The aim of this paper is to improve the Schmidt bound for
![]() $6\leq n\leq 94$
. More precisely, we prove the following result.
$6\leq n\leq 94$
. More precisely, we prove the following result.
Theorem 1.2. For
![]() $n\geq 6$
, we have
$n\geq 6$
, we have
where
![]() $g=\left \lfloor \frac {n-1}2\right \rfloor $
.
$g=\left \lfloor \frac {n-1}2\right \rfloor $
.
For example, the best known bound for the number of isomorphism classes of sextic fields of absolute discriminant less than X was previously
![]() $O(X^2)$
, while Theorem 1.2 yields the bound
$O(X^2)$
, while Theorem 1.2 yields the bound
![]() $O(X^{61/32+\epsilon })$
.
$O(X^{61/32+\epsilon })$
.
Remark 1.3.
(a) In an independent work, Anderson et al. [Reference Anderson, Gafni and Hughes1] also obtain an improvement to Schmidt’s bound, proving that
![]() $N_n(X)\ll _\epsilon X^{(n+2)/4-1/(4n-4)+\epsilon }$
.
$N_n(X)\ll _\epsilon X^{(n+2)/4-1/(4n-4)+\epsilon }$
.
(b) Improvements to Schmidt’s bound in small degrees have played an important role in recent works, such as in proving van der Waerden’s conjecture on Galois groups in small degrees [Reference Bhargava5]; indeed, the improvements contained in Theorem 1.2 also immediately lead to corresponding improvements on the bounds in [Reference Bhargava5].
(c) Schmidt’s original work obtains upper bounds for the number of degree n extensions (with bounded absolute discriminant) of any fixed number field K. In forthcoming work [Reference Bhargava, Shankar and Wang8], we generalise the results of [Reference Bhargava, Shankar and Wang7], obtaining upper bounds for the number of monic polynomials with coefficients in the ring of integers of K, with bounded height and whose discriminants are divisible by the square of a large prime ideal. In combination with the methods of this paper, this will yield improved upper bounds on Schmidt’s result for K.
1.1 Methods
Our proof follows the strategy of [Reference Schmidt14]. For a monic real polynomial
we define the height
![]() $H(f)$
of f by
$H(f)$
of f by
Let K be a number field of degree n having absolute discriminant less than X. Then the lattice
![]() ${\mathcal O}_K^{\mathrm {Tr}=0}$
(viewed as a subset of
${\mathcal O}_K^{\mathrm {Tr}=0}$
(viewed as a subset of
![]() ${\mathbb R}^{n-1}$
via its archimedean embeddings) has covolume at most
${\mathbb R}^{n-1}$
via its archimedean embeddings) has covolume at most
![]() $O(\sqrt {X})$
in
$O(\sqrt {X})$
in
![]() ${\mathbb R}^{n-1}$
; hence, the length of its shortest nonzero vector
${\mathbb R}^{n-1}$
; hence, the length of its shortest nonzero vector
![]() $\alpha $
is at most
$\alpha $
is at most
![]() $O((\sqrt {X})^{1/(n-1)})=O(X^{1/(2n-2)})$
. If K is primitive, in that, K has no nontrivial subfield, then
$O((\sqrt {X})^{1/(n-1)})=O(X^{1/(2n-2)})$
. If K is primitive, in that, K has no nontrivial subfield, then
![]() $K={\mathbb Q}(\alpha )$
since
$K={\mathbb Q}(\alpha )$
since
![]() $\alpha \not \in {\mathbb Q}$
. The minimal polynomial
$\alpha \not \in {\mathbb Q}$
. The minimal polynomial
![]() $f(x)$
of
$f(x)$
of
![]() $\alpha $
is an integer monic polynomial with height at most
$\alpha $
is an integer monic polynomial with height at most
![]() $O(X^{1/(2n-2)})$
and vanishing subleading coefficient. That is, if
$O(X^{1/(2n-2)})$
and vanishing subleading coefficient. That is, if
![]() $f(x)$
is expressed in the form (1.2), then
$f(x)$
is expressed in the form (1.2), then
![]() $a_1=0$
and
$a_1=0$
and
![]() $|a_i|\ll X^{i/(2n-2)}$
for
$|a_i|\ll X^{i/(2n-2)}$
for
![]() $i=2,\ldots ,n$
. Therefore, the total number of primitive number fields of degree n with absolute discriminant less than X is bounded by the number of such monic degree n integer polynomials with height at most
$i=2,\ldots ,n$
. Therefore, the total number of primitive number fields of degree n with absolute discriminant less than X is bounded by the number of such monic degree n integer polynomials with height at most
![]() $O(X^{1/(2n-2)})$
and vanishing subleading coefficient. The number of such polynomials is
$O(X^{1/(2n-2)})$
and vanishing subleading coefficient. The number of such polynomials is
yielding Schmidt’s bound for primitive number fields of degree n. Meanwhile, imprimitive fields of degree n of absolute discriminant at most X can be counted using their proper primitive subextensions (which would, thus, have degree at most
![]() $n/2$
) to obtain the bound
$n/2$
) to obtain the bound
![]() $O(X^{(n/2+2)/4})=O(X^{(n+4)/8})$
, which is much smaller than Schmidt’s bound for primitive fields.
$O(X^{(n/2+2)/4})=O(X^{(n+4)/8})$
, which is much smaller than Schmidt’s bound for primitive fields.
Our improvement on the above argument in the case of primitive fields is based on the following observation: a monic integral polynomial
![]() $f(x)$
of degree n with height
$f(x)$
of degree n with height
![]() $\asymp X^{1/(2n-2)}$
usually has discriminant close to
$\asymp X^{1/(2n-2)}$
usually has discriminant close to
![]() $X^{n/2}$
; in this scenario, if the number field
$X^{n/2}$
; in this scenario, if the number field
![]() $K={\mathbb Q}[x]/(f(x))$
has absolute discriminant less than X, then the discriminant of
$K={\mathbb Q}[x]/(f(x))$
has absolute discriminant less than X, then the discriminant of
![]() $f(x)$
must be divisible by a large square! This is because the discriminant of f is equal to the discriminant of K times the square of the index of
$f(x)$
must be divisible by a large square! This is because the discriminant of f is equal to the discriminant of K times the square of the index of
![]() ${\mathbb Z}[x]/f(x)$
in the ring of integers of K. Thus, to bound the number of primitive number fields K of degree n having absolute discriminant less than X, it suffices to bound the number of monic polynomials of height
${\mathbb Z}[x]/f(x)$
in the ring of integers of K. Thus, to bound the number of primitive number fields K of degree n having absolute discriminant less than X, it suffices to bound the number of monic polynomials of height
![]() $\ll X^{1/(2n-2)}$
with vanishing subleading coefficient whose discriminant is divisible by a large square.
$\ll X^{1/(2n-2)}$
with vanishing subleading coefficient whose discriminant is divisible by a large square.
In previous work [Reference Bhargava, Shankar and Wang7], in order to sieve to squarefree discriminants, we proved an upper bound on the number of monic integral polynomials of degree n and bounded height having discriminant divisible by the square of a large squarefree number; this was accomplished via a lift to pairs of integral n-ary quadratic forms
![]() $(A_0,B)$
where
$(A_0,B)$
where
![]() $A_0$
is split. Specifically, for a positive integer m, let
$A_0$
is split. Specifically, for a positive integer m, let
![]() ${\mathcal W}_m$
denote the set of integer monic polynomials of degree n having discriminant divisible by
${\mathcal W}_m$
denote the set of integer monic polynomials of degree n having discriminant divisible by
![]() $m^2$
. Then, in [Reference Bhargava, Shankar and Wang7, Theorem 4.4], we proved the following theorem:
$m^2$
. Then, in [Reference Bhargava, Shankar and Wang7, Theorem 4.4], we proved the following theorem:
Theorem 1.4. For a real number
![]() $H>1$
, we have
$H>1$
, we have
 $$ \begin{align*} \#\bigcup_{\substack{m>M\\m\mathrm{\:squarefree}}}\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} = O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{\sqrt{M}}\bigg)+O_\epsilon\big(H^{n(n+1)/2-1/5+\epsilon}\big). \end{align*} $$
$$ \begin{align*} \#\bigcup_{\substack{m>M\\m\mathrm{\:squarefree}}}\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} = O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{\sqrt{M}}\bigg)+O_\epsilon\big(H^{n(n+1)/2-1/5+\epsilon}\big). \end{align*} $$
In this paper, we improve upon Theorem 1.4 in two ways. First, we generalise these results to bound the number of monic integer polynomials of degree n having discriminant divisible by the square of a large (not necessarily squarefree) integer. Second, we replace the use of the Selberg sieve in [Reference Bhargava, Shankar and Wang7] by a Hilbert irreducibility theorem (HIT) argument — using the quantitative version of HIT due to Castillo and Dietmann [Reference Castillo and Dietmann9] — to attain an improved error term. We thereby prove the following theorem:
Theorem 1.5. For a real number
![]() $H>1$
, we have
$H>1$
, we have
 $$ \begin{align*} \begin{array}{rcl} \displaystyle \#\bigcup_{\substack{m>M}}\#\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} &=& \displaystyle O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{2/(n+3)-\epsilon}}\bigg)+O\big(H^{n(n+1)/2-1+1/2^{2g}+\epsilon}\big); \\[.25in] \displaystyle \#\bigcup_{\substack{m>M\\m\mathrm{\:squarefree}}}\#\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} &=& \displaystyle O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{\sqrt{M}}\bigg)+O\big(H^{n(n+1)/2-1+1/2^{2g}+\epsilon}\big). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} \displaystyle \#\bigcup_{\substack{m>M}}\#\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} &=& \displaystyle O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{2/(n+3)-\epsilon}}\bigg)+O\big(H^{n(n+1)/2-1+1/2^{2g}+\epsilon}\big); \\[.25in] \displaystyle \#\bigcup_{\substack{m>M\\m\mathrm{\:squarefree}}}\#\big\{f(x)\in {\mathcal W}_m:H(f)<H\big\} &=& \displaystyle O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{\sqrt{M}}\bigg)+O\big(H^{n(n+1)/2-1+1/2^{2g}+\epsilon}\big). \end{array} \end{align*} $$
This improvement to Theorem 1.4 then allows us to deduce Theorem 1.2.
We note that Theorem 1.5 also implies corresponding improvements to the error terms in the main results of [Reference Bhargava, Shankar and Wang7]. Let
![]() $V_n\simeq {\mathbb A}^n$
denote the space of monic polynomials of degree n. An element
$V_n\simeq {\mathbb A}^n$
denote the space of monic polynomials of degree n. An element
![]() $f\in V_n({\mathbb Z})$
is said to be maximal if it has nonzero discriminant and if
$f\in V_n({\mathbb Z})$
is said to be maximal if it has nonzero discriminant and if
![]() ${\mathbb Z}[x]/f(x)$
is the ring of integers of
${\mathbb Z}[x]/f(x)$
is the ring of integers of
![]() ${\mathbb Q}[x]/f(x)$
. Then, for certain constants
${\mathbb Q}[x]/f(x)$
. Then, for certain constants
![]() $\lambda _n>0$
as defined in [Reference Bhargava, Shankar and Wang7, Equation (1)], we prove:
$\lambda _n>0$
as defined in [Reference Bhargava, Shankar and Wang7, Equation (1)], we prove:
Theorem 1.6. We have
 $$ \begin{align*} \begin{array}{rcl} \displaystyle \#\big\{f\in V_n({\mathbb Z}): H(f)<H \mathrm{\;and}\ \Delta(f) \mathrm{\;squarefree}\big\} &=& \displaystyle \lambda_n 2^n H^{\frac{n(n+1)}{2}}+O_\epsilon\bigg( H^{\frac{n(n+1)}{2}-1+\frac{1}{2^{2g}}+\epsilon} \bigg); \\[.2in] \displaystyle \#\big\{f\in V_n({\mathbb Z}): H(f)<H \mathrm{\;and}\ f \mathrm{\;maximal}\big\} &=& \displaystyle \frac{6}{\pi^2} 2^n H^{\frac{n(n+1)}{2}}+O_\epsilon\bigg( H^{\frac{n(n+1)}{2}-1+\frac{1}{2^{2g}}+\epsilon} \bigg). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} \displaystyle \#\big\{f\in V_n({\mathbb Z}): H(f)<H \mathrm{\;and}\ \Delta(f) \mathrm{\;squarefree}\big\} &=& \displaystyle \lambda_n 2^n H^{\frac{n(n+1)}{2}}+O_\epsilon\bigg( H^{\frac{n(n+1)}{2}-1+\frac{1}{2^{2g}}+\epsilon} \bigg); \\[.2in] \displaystyle \#\big\{f\in V_n({\mathbb Z}): H(f)<H \mathrm{\;and}\ f \mathrm{\;maximal}\big\} &=& \displaystyle \frac{6}{\pi^2} 2^n H^{\frac{n(n+1)}{2}}+O_\epsilon\bigg( H^{\frac{n(n+1)}{2}-1+\frac{1}{2^{2g}}+\epsilon} \bigg). \end{array} \end{align*} $$
This improves upon [Reference Bhargava, Shankar and Wang7, Equation (4)], where the error terms were
![]() $O\big ( H^{\frac {n(n+1)}{2}-\frac 15+\epsilon }\big )$
. One direct consequence of this improvement is improved level-of-distribution results when counting monic polynomials
$O\big ( H^{\frac {n(n+1)}{2}-\frac 15+\epsilon }\big )$
. One direct consequence of this improvement is improved level-of-distribution results when counting monic polynomials
![]() $f(x)$
, such that
$f(x)$
, such that
![]() $\Delta (f)$
is squarefree (respectively,
$\Delta (f)$
is squarefree (respectively,
![]() $f(x)$
is maximal) that satisfy splitting conditions modulo finitely many primes. A concrete application concerns the distribution of low-lying zeroes of the Dedekind zeta functions of monogenised number fields of degree n (a pair
$f(x)$
is maximal) that satisfy splitting conditions modulo finitely many primes. A concrete application concerns the distribution of low-lying zeroes of the Dedekind zeta functions of monogenised number fields of degree n (a pair
![]() $(K,\alpha )$
, where K is a number field and
$(K,\alpha )$
, where K is a number field and
![]() $\alpha $
is an element in the ring of integers of K, is said to be monogenised if
$\alpha $
is an element in the ring of integers of K, is said to be monogenised if
![]() ${\mathbb Z}[\alpha ]$
is the ring of integers of K). In [Reference Shankar, Södergren and Templier15, §5], it was shown that this family of zeta functions has symplectic symmetry type, via a computation of the
${\mathbb Z}[\alpha ]$
is the ring of integers of K). In [Reference Shankar, Södergren and Templier15, §5], it was shown that this family of zeta functions has symplectic symmetry type, via a computation of the
![]() $1$
-level density with respect to test functions whose Fourier transforms have bounded support in
$1$
-level density with respect to test functions whose Fourier transforms have bounded support in
![]() $[-\alpha ,\alpha ]$
for
$[-\alpha ,\alpha ]$
for
![]() $\alpha <2/(5n(n+1)(2n+1))$
. Theorem 1.5 implies that we can, in fact, take
$\alpha <2/(5n(n+1)(2n+1))$
. Theorem 1.5 implies that we can, in fact, take
![]() $\alpha <2/((1-2^{-2g})n(n+1)(2n+1))$
. Improved level-of-distribution results in this setting also have applications towards proving the existence of number fields of degree n whose discriminants have a bounded number of prime factors (see [Reference Taniguchi and Thorne17], where such results are proved for cubic and quartic fields).
$\alpha <2/((1-2^{-2g})n(n+1)(2n+1))$
. Improved level-of-distribution results in this setting also have applications towards proving the existence of number fields of degree n whose discriminants have a bounded number of prime factors (see [Reference Taniguchi and Thorne17], where such results are proved for cubic and quartic fields).
1.2 Organisation
This paper is organised as follows. In §2, we bound the number of monic integer polynomials of degree n and height less than H that have discriminant smaller than the expected size
![]() $\asymp H^{n(n-1)}$
. In §3, we then consider the set of monic integer polynomials of degree n with discriminant divisible by the square of a large, not-necessarily squarefree integer. We partition this set into two subsets whose sizes we effectively bound using a geometric sieve argument (as in [Reference Bhargava4]) and via a lift to pairs of quadratic forms
$\asymp H^{n(n-1)}$
. In §3, we then consider the set of monic integer polynomials of degree n with discriminant divisible by the square of a large, not-necessarily squarefree integer. We partition this set into two subsets whose sizes we effectively bound using a geometric sieve argument (as in [Reference Bhargava4]) and via a lift to pairs of quadratic forms
![]() $(A_0,B)$
(as in [Reference Bhargava, Shankar and Wang7]), respectively. In §4, we describe how to replace the Selberg sieve argument of [Reference Bhargava, Shankar and Wang7] by a quantitative Hilbert irreducibility argument using the work of Castillo and Dietmann [Reference Castillo and Dietmann9] to improve error terms. Finally, in §5, we combine the results of §2–§4 to prove Theorems 1.2, 1.5 and 1.6.
$(A_0,B)$
(as in [Reference Bhargava, Shankar and Wang7]), respectively. In §4, we describe how to replace the Selberg sieve argument of [Reference Bhargava, Shankar and Wang7] by a quantitative Hilbert irreducibility argument using the work of Castillo and Dietmann [Reference Castillo and Dietmann9] to improve error terms. Finally, in §5, we combine the results of §2–§4 to prove Theorems 1.2, 1.5 and 1.6.
2 The number of monic polynomials of bounded height and small discriminant
The following proposition shows that most monic integer polynomials of degree n with vanishing subleading coefficient and height less than H have discriminant close to
![]() $H^{n(n-1)}$
.
$H^{n(n-1)}$
.
Proposition 2.1. Let
![]() $0<\kappa <n(n-1)$
. The number of monic integer polynomials having degree n, vanishing subleading coefficient, height less than H and absolute discriminant less than
$0<\kappa <n(n-1)$
. The number of monic integer polynomials having degree n, vanishing subleading coefficient, height less than H and absolute discriminant less than
![]() $H^{n(n-1)-\kappa }$
is at most
$H^{n(n-1)-\kappa }$
is at most
![]() $O(H^{(n-1)(n+2)/2 - {\kappa }/{(n-1)}})$
, where the implied constant depends only on n.
$O(H^{(n-1)(n+2)/2 - {\kappa }/{(n-1)}})$
, where the implied constant depends only on n.
Proof. Let
![]() $\eta = \kappa /(n-1)$
. Let
$\eta = \kappa /(n-1)$
. Let
![]() $a_2,\ldots ,a_{n-1}$
be integers with
$a_2,\ldots ,a_{n-1}$
be integers with
![]() $|a_i|<H^i$
for
$|a_i|<H^i$
for
![]() $i=2,\ldots ,n-1$
. The discriminant of
$i=2,\ldots ,n-1$
. The discriminant of
![]() $x^n + a_2x^{n-2} + \cdots + a_n$
is a polynomial
$x^n + a_2x^{n-2} + \cdots + a_n$
is a polynomial
![]() $F(a_n)$
in
$F(a_n)$
in
![]() $a_n$
of degree
$a_n$
of degree
![]() $n-1$
with leading term
$n-1$
with leading term
![]() $C_n a_n^{n-1}$
, where
$C_n a_n^{n-1}$
, where
![]() $C_n$
is a nonzero constant. Let
$C_n$
is a nonzero constant. Let
![]() $s_1,\ldots ,s_{n-1}\in {\mathbb C}$
be the
$s_1,\ldots ,s_{n-1}\in {\mathbb C}$
be the
![]() $n-1$
roots of
$n-1$
roots of
![]() $F(x)$
. Then
$F(x)$
. Then
Since
![]() $|F(a_n)| \leq H^{n(n-1)-\kappa }$
, it follows that
$|F(a_n)| \leq H^{n(n-1)-\kappa }$
, it follows that
![]() $|(a_n-s_1)\cdots (a_n-s_{n-1})|\ll _n H^{n(n-1)-\kappa }$
. Hence,
$|(a_n-s_1)\cdots (a_n-s_{n-1})|\ll _n H^{n(n-1)-\kappa }$
. Hence,
for some
![]() $i\in \{1,\ldots ,n-1\}$
. The number of integers
$i\in \{1,\ldots ,n-1\}$
. The number of integers
![]() $a_n$
satisfying (2.1) for some i is
$a_n$
satisfying (2.1) for some i is
![]() $O(H^{n-\eta }+1)$
. Multiplying this by the number of choices for
$O(H^{n-\eta }+1)$
. Multiplying this by the number of choices for
![]() $a_2,\ldots ,a_{n-1}$
then gives the desired bound.
$a_2,\ldots ,a_{n-1}$
then gives the desired bound.
3 The divisibility of discriminants of polynomials by large squares
In this section, we consider the set
![]() ${\mathcal W}_m$
of monic integer polynomials of degree n having discriminant divisible by
${\mathcal W}_m$
of monic integer polynomials of degree n having discriminant divisible by
![]() $m^2$
. First, for a prime power
$m^2$
. First, for a prime power
![]() $m=p^k$
, we write the set
$m=p^k$
, we write the set
![]() ${\mathcal W}_{p^k}$
of polynomials naturally as a union of two sets. The first set consists of polynomials
${\mathcal W}_{p^k}$
of polynomials naturally as a union of two sets. The first set consists of polynomials
![]() $f\in {\mathcal W}_{p^k}$
satisfying
$f\in {\mathcal W}_{p^k}$
satisfying
![]() $p^k\mid \gcd (\Delta (f),\Delta '(f))$
for some specifically constructed polynomial
$p^k\mid \gcd (\Delta (f),\Delta '(f))$
for some specifically constructed polynomial
![]() $\Delta '(f)$
in the coefficients of f. The first set is designed so that a suitable extension of the techniques of [Reference Bhargava4] can be applied to bound the number of elements of bounded height in this first set. The second set consists of polynomials
$\Delta '(f)$
in the coefficients of f. The first set is designed so that a suitable extension of the techniques of [Reference Bhargava4] can be applied to bound the number of elements of bounded height in this first set. The second set consists of polynomials
![]() $f\in {\mathcal W}_{p^k}$
for which there exists some
$f\in {\mathcal W}_{p^k}$
for which there exists some
![]() $r\in {\mathbb Z}$
, such that
$r\in {\mathbb Z}$
, such that
![]() $f(r)$
and
$f(r)$
and
![]() $f'(r)$
are both divisible by a high power of p. The second set is designed so that a suitable adaptation of the methods of [Reference Bhargava, Shankar and Wang7] can be applied to bound the number of elements of bounded height in this second set. Finally, by using the case of prime powers
$f'(r)$
are both divisible by a high power of p. The second set is designed so that a suitable adaptation of the methods of [Reference Bhargava, Shankar and Wang7] can be applied to bound the number of elements of bounded height in this second set. Finally, by using the case of prime powers
![]() $m=p^k$
, we show that
$m=p^k$
, we show that
![]() ${\mathcal W}_m$
, for a general positive integer m, can also be expressed as the union of two sets, on which suitable extensions of the methods from [Reference Bhargava4] and [Reference Bhargava, Shankar and Wang7], respectively, can be applied to bound the number of elements in
${\mathcal W}_m$
, for a general positive integer m, can also be expressed as the union of two sets, on which suitable extensions of the methods from [Reference Bhargava4] and [Reference Bhargava, Shankar and Wang7], respectively, can be applied to bound the number of elements in
![]() ${\mathcal W}_m$
of bounded height.
${\mathcal W}_m$
of bounded height.
We begin by defining
![]() $\Delta '$
. For any monic polynomial
$\Delta '$
. For any monic polynomial
![]() $f(x) = x^n + a_1x^{n-1} + \cdots + a_n$
of degree n, its discriminant
$f(x) = x^n + a_1x^{n-1} + \cdots + a_n$
of degree n, its discriminant
![]() $\Delta (f)=\Delta (a_1,\ldots ,a_n)$
can be viewed as a polynomial in
$\Delta (f)=\Delta (a_1,\ldots ,a_n)$
can be viewed as a polynomial in
![]() $a_1,\ldots ,a_n$
with integer coefficients. Let
$a_1,\ldots ,a_n$
with integer coefficients. Let
![]() $r_1,\ldots ,r_n$
denote the n roots of
$r_1,\ldots ,r_n$
denote the n roots of
![]() $f(x)$
. Define
$f(x)$
. Define
 $$ \begin{align*}\Delta'(f) = \sum_{i<j} \frac{\Delta(f)}{(r_i-r_j)^2}.\end{align*} $$
$$ \begin{align*}\Delta'(f) = \sum_{i<j} \frac{\Delta(f)}{(r_i-r_j)^2}.\end{align*} $$
Note that we may represent
![]() $\Delta '(f)$
as a polynomial
$\Delta '(f)$
as a polynomial
![]() $\Delta '(a_1,\ldots ,a_n)$
in
$\Delta '(a_1,\ldots ,a_n)$
in
![]() $a_1,\ldots ,a_n$
with integer coefficients, since it is a symmetric polynomial in
$a_1,\ldots ,a_n$
with integer coefficients, since it is a symmetric polynomial in
![]() $r_1,\ldots ,r_n$
with integer coefficients.
$r_1,\ldots ,r_n$
with integer coefficients.
Recall that
![]() $V_n\simeq {\mathbb A}^n$
denotes the space of monic polynomials of degree n. For a positive integer m, define the sets
$V_n\simeq {\mathbb A}^n$
denotes the space of monic polynomials of degree n. For a positive integer m, define the sets
 $$ \begin{align*} {\mathcal W}_m &= \{f\in V_n({\mathbb Z}) \colon m^2\mid \Delta(f),\,\,\Delta(f)\neq 0\};\\[.05in] {\mathcal W}_{m}^{(1)} &= \{f\in {\mathcal W}_m \colon m\mid \Delta'(f)\};\\[.05in] {\mathcal W}_{m}^{(2)} &= \{f\in {\mathcal W}_m \colon \exists r\in{\mathbb Z} \mbox{ such that }m\mid f'(r),\;m^2\mid f(r)\}. \end{align*} $$
$$ \begin{align*} {\mathcal W}_m &= \{f\in V_n({\mathbb Z}) \colon m^2\mid \Delta(f),\,\,\Delta(f)\neq 0\};\\[.05in] {\mathcal W}_{m}^{(1)} &= \{f\in {\mathcal W}_m \colon m\mid \Delta'(f)\};\\[.05in] {\mathcal W}_{m}^{(2)} &= \{f\in {\mathcal W}_m \colon \exists r\in{\mathbb Z} \mbox{ such that }m\mid f'(r),\;m^2\mid f(r)\}. \end{align*} $$
We begin with the following result on
![]() ${\mathcal W}_{p^k}$
for a prime power
${\mathcal W}_{p^k}$
for a prime power
![]() $p^k$
.
$p^k$
.
Lemma 3.1. Let p be an odd prime and k be any positive integer. Then
 $$ \begin{align*} \begin{array}{rcl} \displaystyle {\mathcal W}_{p^k} &\subset& \displaystyle {\mathcal W}_{p^k}^{(1)} \cup {\mathcal W}_{p^{\lceil k/2\rceil}}^{(2)}; \\[.1in]\displaystyle \displaystyle {\mathcal W}_{2^k} &\subset& \displaystyle {\mathcal W}_{2^k}^{(1)} \cup {\mathcal W}_{2^{\lceil k/2\rceil-1}}^{(2)}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} \displaystyle {\mathcal W}_{p^k} &\subset& \displaystyle {\mathcal W}_{p^k}^{(1)} \cup {\mathcal W}_{p^{\lceil k/2\rceil}}^{(2)}; \\[.1in]\displaystyle \displaystyle {\mathcal W}_{2^k} &\subset& \displaystyle {\mathcal W}_{2^k}^{(1)} \cup {\mathcal W}_{2^{\lceil k/2\rceil-1}}^{(2)}. \end{array} \end{align*} $$
Proof. Let
![]() $v_p$
denote the p-adic valuation. Suppose
$v_p$
denote the p-adic valuation. Suppose
![]() $f(x)\in {\mathcal W}_{p^k}$
, and let
$f(x)\in {\mathcal W}_{p^k}$
, and let
![]() $\ell = v_p(\Delta (f))\geq 2k$
. Let
$\ell = v_p(\Delta (f))\geq 2k$
. Let
![]() $r_1,\ldots ,r_n$
denote the n roots of
$r_1,\ldots ,r_n$
denote the n roots of
![]() $f(x)$
in
$f(x)$
in
![]() $\overline {{\mathbb Q}_p}$
. Suppose the p-adic valuation
$\overline {{\mathbb Q}_p}$
. Suppose the p-adic valuation
![]() $\theta = v_p(r_1-r_2)$
is the largest among all differences of roots of
$\theta = v_p(r_1-r_2)$
is the largest among all differences of roots of
![]() $f(x).$
Then
$f(x).$
Then
![]() $p^{\ell -2\theta }\mid \Delta '(f)$
. If
$p^{\ell -2\theta }\mid \Delta '(f)$
. If
![]() $\theta \leq (\ell -k)/2$
, then
$\theta \leq (\ell -k)/2$
, then
![]() $f\in {\mathcal W}_{p^k}^{(1)}$
.
$f\in {\mathcal W}_{p^k}^{(1)}$
.
Now suppose that
![]() $\theta> (\ell -k)/2\geq k/2$
. Then
$\theta> (\ell -k)/2\geq k/2$
. Then
![]() $v_p(r_i-r_j)<\theta $
for all distinct pairs
$v_p(r_i-r_j)<\theta $
for all distinct pairs
![]() $i,j$
with
$i,j$
with
![]() $\{i,j\}\neq \{1,2\}$
; indeed, if
$\{i,j\}\neq \{1,2\}$
; indeed, if
![]() $v_p(r_i-r_j)=\theta $
, then
$v_p(r_i-r_j)=\theta $
, then
![]() $(r_1-r_2)^2(r_i-r_j)^2\mid \Delta (f)$
implying
$(r_1-r_2)^2(r_i-r_j)^2\mid \Delta (f)$
implying
![]() $\ell \geq 4\theta>2\ell -2k$
, a contradiction. Thus, either
$\ell \geq 4\theta>2\ell -2k$
, a contradiction. Thus, either
![]() $r_1,r_2$
are defined over
$r_1,r_2$
are defined over
![]() ${\mathbb Q}_p$
or are conjugate over some quadratic extension of
${\mathbb Q}_p$
or are conjugate over some quadratic extension of
![]() ${\mathbb Q}_p$
. That is, we have
${\mathbb Q}_p$
. That is, we have
![]() $q(x) = (x-r_1)(x-r_2) = x^2 - bx + c$
for some
$q(x) = (x-r_1)(x-r_2) = x^2 - bx + c$
for some
![]() $b,c\in {\mathbb Z}_p$
. We claim that
$b,c\in {\mathbb Z}_p$
. We claim that
![]() $b/2\in {\mathbb Z}_p$
. This is clear for
$b/2\in {\mathbb Z}_p$
. This is clear for
![]() $p\neq 2$
, while if
$p\neq 2$
, while if
![]() $p=2$
, then
$p=2$
, then
![]() $b^2 - 4c = (r_1-r_2)^2$
is divisible by
$b^2 - 4c = (r_1-r_2)^2$
is divisible by
![]() $2^{2\theta }$
and, hence, is divisible by
$2^{2\theta }$
and, hence, is divisible by
![]() $2^2$
since
$2^2$
since
![]() $\theta>k/2\geq 1/2$
.
$\theta>k/2\geq 1/2$
.
Now
![]() $q(b/2) = - \frac 14(r_1-r_2)^2$
and
$q(b/2) = - \frac 14(r_1-r_2)^2$
and
![]() $q'(b/2) = 0$
. Since
$q'(b/2) = 0$
. Since
![]() $f(x) = q(x)h(x)$
for some
$f(x) = q(x)h(x)$
for some
![]() $h(x)\in {\mathbb Z}_p[x]$
, we have that
$h(x)\in {\mathbb Z}_p[x]$
, we have that
![]() $\frac 14(r_1-r_2)^2$
divides
$\frac 14(r_1-r_2)^2$
divides
![]() $f(b/2)$
and
$f(b/2)$
and
![]() $f'(b/2)$
. Hence,
$f'(b/2)$
. Hence,
![]() $f\in {\mathcal W}_{p^e}^{(2)}$
, where
$f\in {\mathcal W}_{p^e}^{(2)}$
, where
![]() $e= \lceil \theta \rceil - v_p(2)$
.
$e= \lceil \theta \rceil - v_p(2)$
.
We now prove the main result of this section.
Proposition 3.2. Let M be any positive real number, and let
![]() $q_1 = \lfloor (M/2)^{\alpha }\rfloor $
,
$q_1 = \lfloor (M/2)^{\alpha }\rfloor $
,
![]() $q_2 = \lfloor (M/2)^{\beta }\rfloor $
, where
$q_2 = \lfloor (M/2)^{\beta }\rfloor $
, where
![]() $\alpha ,\beta $
are positive real numbers, such that
$\alpha ,\beta $
are positive real numbers, such that
![]() $\alpha + 2\beta = 1$
. Then
$\alpha + 2\beta = 1$
. Then
 $$ \begin{align*} \begin{array}{rcl} \displaystyle\bigcup_{\substack{m>M\\ m {\:\mathrm{squarefree}}}}{\mathcal W}_m &\subset& \displaystyle\bigcup_{m>\sqrt{M}}{\mathcal W}_{m}^{(1)}\cup \bigcup_{m>\sqrt{M}}{\mathcal W}_{m}^{(2)}; \\[.375in] \displaystyle\bigcup_{m>M}{\mathcal W}_m &\subset& \displaystyle\bigcup_{m>q_1}{\mathcal W}_{m}^{(1)}\cup \bigcup_{m>q_2}{\mathcal W}_{m}^{(2)}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} \displaystyle\bigcup_{\substack{m>M\\ m {\:\mathrm{squarefree}}}}{\mathcal W}_m &\subset& \displaystyle\bigcup_{m>\sqrt{M}}{\mathcal W}_{m}^{(1)}\cup \bigcup_{m>\sqrt{M}}{\mathcal W}_{m}^{(2)}; \\[.375in] \displaystyle\bigcup_{m>M}{\mathcal W}_m &\subset& \displaystyle\bigcup_{m>q_1}{\mathcal W}_{m}^{(1)}\cup \bigcup_{m>q_2}{\mathcal W}_{m}^{(2)}. \end{array} \end{align*} $$
Proof. The first containment is proved in the proof of [Reference Bhargava, Shankar and Wang7, Theorem 4.4]. To obtain the second containment, fix
![]() $f\in {\mathcal W}_m$
for some
$f\in {\mathcal W}_m$
for some
![]() $m>M$
. Let
$m>M$
. Let
![]() $\prod _{i=1}^n p_i^{k_i}$
be the prime factorisation of m, and let
$\prod _{i=1}^n p_i^{k_i}$
be the prime factorisation of m, and let
 $$ \begin{align*}m_1 = \prod_{p_i\colon f\in {\mathcal W}_{p_i^{k_i}}^{(1)}} p_i^{k_i},\qquad m_2 = \prod_{p_i\colon f\in {\mathcal W}_{p_i^{\lceil k_i/2\rceil-v_{p_i}(2)}}^{(2)}} p_i^{\lceil k_i/2\rceil-v_{p_i}(2)}.\end{align*} $$
$$ \begin{align*}m_1 = \prod_{p_i\colon f\in {\mathcal W}_{p_i^{k_i}}^{(1)}} p_i^{k_i},\qquad m_2 = \prod_{p_i\colon f\in {\mathcal W}_{p_i^{\lceil k_i/2\rceil-v_{p_i}(2)}}^{(2)}} p_i^{\lceil k_i/2\rceil-v_{p_i}(2)}.\end{align*} $$
Then
![]() $f\in {\mathcal W}_{m_1}^{(1)}\cup {\mathcal W}_{m_2}^{(2)}$
and
$f\in {\mathcal W}_{m_1}^{(1)}\cup {\mathcal W}_{m_2}^{(2)}$
and
![]() $m_1m_2^2\geq m/2> M/2$
. Hence, either
$m_1m_2^2\geq m/2> M/2$
. Hence, either
![]() $m_1>q_1$
or
$m_1>q_1$
or
![]() $m_2>q_2$
, and, therefore,
$m_2>q_2$
, and, therefore,
![]() $f\in \bigcup _{m>q_1}{\mathcal W}_{m}^{(1)}\cup \bigcup _{m>q_2}{\mathcal W}_{m}^{(2)}$
, as desired.
$f\in \bigcup _{m>q_1}{\mathcal W}_{m}^{(1)}\cup \bigcup _{m>q_2}{\mathcal W}_{m}^{(2)}$
, as desired.
4 A rational root criterion for being distinguished
Let
![]() $A_0$
denote the
$A_0$
denote the
![]() $n\times n$
symmetric matrix with
$n\times n$
symmetric matrix with
![]() $1$
’s on the antidiagonal and
$1$
’s on the antidiagonal and
![]() $0$
’s elsewhere. Let W denote the space of
$0$
’s elsewhere. Let W denote the space of
![]() $n\times n$
symmetric matrices. We recall from [Reference Bhargava and Gross6, Reference Shankar and Wang16] the following definition of a distinguished element
$n\times n$
symmetric matrices. We recall from [Reference Bhargava and Gross6, Reference Shankar and Wang16] the following definition of a distinguished element
![]() $B\in W({\mathbb Q})$
. If
$B\in W({\mathbb Q})$
. If
![]() $n=2g+1$
is odd, then an element
$n=2g+1$
is odd, then an element
![]() $B\in W({\mathbb Q})$
with
$B\in W({\mathbb Q})$
with
![]() $\Delta (B)\neq 0$
is distinguished if there exists a g-plane Y defined over
$\Delta (B)\neq 0$
is distinguished if there exists a g-plane Y defined over
![]() ${\mathbb Q}$
that is isotropic with respect to the quadratic forms defined by
${\mathbb Q}$
that is isotropic with respect to the quadratic forms defined by
![]() $A_0$
and B. When
$A_0$
and B. When
![]() $n = 2g+2$
is even, then B is distinguished if there exists a g-plane Y defined over
$n = 2g+2$
is even, then B is distinguished if there exists a g-plane Y defined over
![]() ${\mathbb Q}$
, such that
${\mathbb Q}$
, such that
![]() $\mathrm {Span}(Y,TY)$
is isotropic with respect to the quadratic form defined by
$\mathrm {Span}(Y,TY)$
is isotropic with respect to the quadratic form defined by
![]() $A_0$
, where
$A_0$
, where
![]() $T = A_0^{-1}B$
.
$T = A_0^{-1}B$
.
We use
![]() $b_{11},b_{12},\ldots ,b_{nn}$
to denote the (indeterminate) entries of B. The goal of this section is to construct a polynomial
$b_{11},b_{12},\ldots ,b_{nn}$
to denote the (indeterminate) entries of B. The goal of this section is to construct a polynomial
![]() $F(B,x)=F(b_{11},b_{12},\ldots ,b_{nn},x)$
that is irreducible generically but has a rational root in x if B is distinguished. The construction of this polynomial will allow us to use a quantitative Hilbert irreducibility argument [Reference Castillo and Dietmann9] to bound the number of distinguished elements in bounded regions.
$F(B,x)=F(b_{11},b_{12},\ldots ,b_{nn},x)$
that is irreducible generically but has a rational root in x if B is distinguished. The construction of this polynomial will allow us to use a quantitative Hilbert irreducibility argument [Reference Castillo and Dietmann9] to bound the number of distinguished elements in bounded regions.
Theorem 4.1. Suppose
![]() $n = 2g+1$
is odd. There exists a polynomial
$n = 2g+1$
is odd. There exists a polynomial
![]() $F(B,x)\in {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][x]$
of degree
$F(B,x)\in {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][x]$
of degree
![]() $2^{2g}$
that is irreducible in
$2^{2g}$
that is irreducible in
![]() ${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn})[x]$
, such that for any
${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn})[x]$
, such that for any
![]() $B_0\in W({\mathbb Q})$
, if
$B_0\in W({\mathbb Q})$
, if
![]() $B_0$
is distinguished, then
$B_0$
is distinguished, then
![]() $F(B_0,x)\in {\mathbb Q}[\sqrt {-1}][x]$
has a root in
$F(B_0,x)\in {\mathbb Q}[\sqrt {-1}][x]$
has a root in
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Proof. Let
![]() $B\in W$
be the generic element. Fix
$B\in W$
be the generic element. Fix
![]() $P\in M_n({\mathbb Q}[\sqrt {-1}])$
, such that
$P\in M_n({\mathbb Q}[\sqrt {-1}])$
, such that
![]() $PA_0P^t$
is the identity matrix
$PA_0P^t$
is the identity matrix
![]() $I_n$
. Let
$I_n$
. Let
![]() $B' = PBP^t$
. Then the entries of
$B' = PBP^t$
. Then the entries of
![]() $B'$
lie in
$B'$
lie in
![]() ${\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}]$
. Let
${\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}]$
. Let
![]() $c_1,\ldots ,c_n \in \overline {{\mathbb Q}(b_{11},\ldots ,b_{nn})}$
be the eigenvalues of
$c_1,\ldots ,c_n \in \overline {{\mathbb Q}(b_{11},\ldots ,b_{nn})}$
be the eigenvalues of
![]() $B'$
, and let
$B'$
, and let
![]() $h(c_1,\ldots ,c_n)\in \text {O}_n({\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n))$
be a change-of-basis matrix, such that
$h(c_1,\ldots ,c_n)\in \text {O}_n({\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n))$
be a change-of-basis matrix, such that
![]() $h(c_1,\ldots ,c_n)B'h(c_1,\ldots ,c_n)^t = B'' = \text {diag}(c_1,\ldots ,c_n)$
. Note that we have fixed an order of the eigenvalues here. For any other order, we simply multiply
$h(c_1,\ldots ,c_n)B'h(c_1,\ldots ,c_n)^t = B'' = \text {diag}(c_1,\ldots ,c_n)$
. Note that we have fixed an order of the eigenvalues here. For any other order, we simply multiply
![]() $h(c_1,\ldots ,c_n)$
by the corresponding permutation matrix.
$h(c_1,\ldots ,c_n)$
by the corresponding permutation matrix.
Following [Reference Wang18, §2], we now have the following explicit construction of the
![]() $2^{2g}$
common isotropic g-planes with respect to the quadratic forms defined by
$2^{2g}$
common isotropic g-planes with respect to the quadratic forms defined by
![]() $I_n$
and
$I_n$
and
![]() $B''$
. Let
$B''$
. Let
![]() $D_1,\ldots ,D_{n} \in {\mathbb Q}(c_1,\ldots ,c_n)$
be a nonzero solution to the following system of linear equations:
$D_1,\ldots ,D_{n} \in {\mathbb Q}(c_1,\ldots ,c_n)$
be a nonzero solution to the following system of linear equations:
 $$ \begin{align*} D_1 + D_2 + \cdots + D_n &= 0\\ D_1c_1 + D_2c_2 + \cdots + D_nc_n &= 0\\ &\vdots \\ D_1c_1^{2g-1} + D_2c_2^{2g-1} + \cdots + D_nc_n^{2g-1} &=0. \end{align*} $$
$$ \begin{align*} D_1 + D_2 + \cdots + D_n &= 0\\ D_1c_1 + D_2c_2 + \cdots + D_nc_n &= 0\\ &\vdots \\ D_1c_1^{2g-1} + D_2c_2^{2g-1} + \cdots + D_nc_n^{2g-1} &=0. \end{align*} $$
Note that we may take
This is obtained by noting that the kernel of an incomplete Vandermonde matrix is spanned by the last row of the inverse of the completed Vandermonde matrix. None of the
![]() $D_i$
is equal to
$D_i$
is equal to
![]() $0$
, and so for each choice of
$0$
, and so for each choice of
![]() $d_i\in {\mathbb Q}(\sqrt {D_i})$
with
$d_i\in {\mathbb Q}(\sqrt {D_i})$
with
![]() $d_i^2 = D_i$
, we have a g-plane
$d_i^2 = D_i$
, we have a g-plane
which is isotropic with respect to the quadratic forms defined by
![]() $I_n$
and
$I_n$
and
![]() $B''$
. Negating all of the
$B''$
. Negating all of the
![]() $d_i$
’s gives the same Y, and so we have
$d_i$
’s gives the same Y, and so we have
![]() $2^{2g}$
distinct g-planes. Now
$2^{2g}$
distinct g-planes. Now
gives a g-plane that is isotropic with respect to the quadratic forms defined
![]() $A_0$
and B, where each
$A_0$
and B, where each
![]() $\ell _{ij}$
is a linear form in
$\ell _{ij}$
is a linear form in
![]() $d_1,\ldots ,d_n$
with coefficients in
$d_1,\ldots ,d_n$
with coefficients in
![]() ${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n)$
.
${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n)$
.
Next we apply the Plücker embedding to send each
![]() $P^th(c_1,\ldots ,c_n)^tY$
to a point
$P^th(c_1,\ldots ,c_n)^tY$
to a point
in projective space, where each
![]() $G_i$
is a homogeneous polynomial of degree g with coefficients in
$G_i$
is a homogeneous polynomial of degree g with coefficients in
![]() ${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n).$
As
${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n).$
As
![]() $d_1,\ldots ,d_{n}$
vary, we get
$d_1,\ldots ,d_{n}$
vary, we get
![]() $2^{2g}$
points
$2^{2g}$
points
![]() $P_1,\ldots ,P_{2^{2g}}$
this way. Now let
$P_1,\ldots ,P_{2^{2g}}$
this way. Now let
![]() $L_1(x_0,\ldots ,x_N) = \alpha _0x_0 + \cdots + \alpha _Nx_N$
and
$L_1(x_0,\ldots ,x_N) = \alpha _0x_0 + \cdots + \alpha _Nx_N$
and
![]() $L_2(x_0,\ldots ,x_N) = \beta _0x_0 + \cdots + \beta _Nx_N$
be two linear forms with integer coefficients
$L_2(x_0,\ldots ,x_N) = \beta _0x_0 + \cdots + \beta _Nx_N$
be two linear forms with integer coefficients
![]() $\alpha _i,\beta _i$
to be chosen later. For
$\alpha _i,\beta _i$
to be chosen later. For
![]() $i = 1,\ldots ,2^{2g}$
, let
$i = 1,\ldots ,2^{2g}$
, let
For now, we only require that none of the
![]() $Q_i$
equals
$Q_i$
equals
![]() $[1:0]$
. We then see that there is a binary
$[1:0]$
. We then see that there is a binary
![]() $2^{2g}$
-ic form
$2^{2g}$
-ic form
![]() $J(c_1,\ldots ,c_n)(x,y)$
defined over
$J(c_1,\ldots ,c_n)(x,y)$
defined over
![]() ${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n)$
vanishing on
${\mathbb Q}[\sqrt {-1}](b_{11},\ldots ,b_{nn},c_1,\ldots ,c_n)$
vanishing on
![]() $Q_1,\ldots ,Q_{2^{2g}}$
. By scaling, we may assume that
$Q_1,\ldots ,Q_{2^{2g}}$
. By scaling, we may assume that
Let
![]() $J_1(c_1,\ldots ,c_n)(x) = J(c_1,\ldots ,c_n)(x,1)$
. Note that if
$J_1(c_1,\ldots ,c_n)(x) = J(c_1,\ldots ,c_n)(x,1)$
. Note that if
![]() $B_0\in W({\mathbb Q})$
is distinguished, then one of the
$B_0\in W({\mathbb Q})$
is distinguished, then one of the
![]() $P_i$
is defined over
$P_i$
is defined over
![]() ${\mathbb Q}$
, in which case,
${\mathbb Q}$
, in which case,
![]() $J_1(c_1,\ldots ,c_n)(x)$
has a root over
$J_1(c_1,\ldots ,c_n)(x)$
has a root over
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Finally, we note that the homogeneous polynomials
![]() $G_0,\ldots ,G_N$
are independent of the ordering of the eigenvalues
$G_0,\ldots ,G_N$
are independent of the ordering of the eigenvalues
![]() $c_1,\ldots ,c_n$
, since permuting the
$c_1,\ldots ,c_n$
, since permuting the
![]() $c_i$
’s permutes the coordinates of Y, which is then cancelled by the extra permutation matrix in
$c_i$
’s permutes the coordinates of Y, which is then cancelled by the extra permutation matrix in
![]() $h(c_1,\ldots ,c_n)$
. Therefore, the coefficients of
$h(c_1,\ldots ,c_n)$
. Therefore, the coefficients of
![]() $J_1(c_1,\ldots ,c_n)(x)$
are symmetric in
$J_1(c_1,\ldots ,c_n)(x)$
are symmetric in
![]() $c_1,\ldots ,c_n$
and so are polynomials in the coefficients of the characteristic polynomial of B. We let
$c_1,\ldots ,c_n$
and so are polynomials in the coefficients of the characteristic polynomial of B. We let
![]() $F(B,x)$
denote this polynomial.
$F(B,x)$
denote this polynomial.
It remains to prove that for some choice of coefficients
![]() $\alpha _i,\beta _i$
for the linear forms
$\alpha _i,\beta _i$
for the linear forms
![]() $L_1,L_2$
, the polynomial
$L_1,L_2$
, the polynomial
![]() $F(B,x)\in {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][x]$
is irreducible. It suffices to exhibit some
$F(B,x)\in {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][x]$
is irreducible. It suffices to exhibit some
![]() $B_0\in W({\mathbb Q}[\sqrt {-1}])$
, such that
$B_0\in W({\mathbb Q}[\sqrt {-1}])$
, such that
![]() $G_{{\mathbb Q}[\sqrt {-1}]}$
, the absolute Galois group of
$G_{{\mathbb Q}[\sqrt {-1}]}$
, the absolute Galois group of
![]() ${\mathbb Q}[\sqrt {-1}]$
, acts transitively on the
${\mathbb Q}[\sqrt {-1}]$
, acts transitively on the
![]() $2^{2g}$
distinct roots of
$2^{2g}$
distinct roots of
![]() $F(B_0,x)$
. For any
$F(B_0,x)$
. For any
![]() $c_1,\ldots ,c_n$
, let
$c_1,\ldots ,c_n$
, let
![]() $E_i=(c_1-c_i)\cdots (c_{i-1}-c_i)(c_{i+1}-c_i)\cdots (c_n-c_i) = \pm D_i^{-1}$
. Let M be a large integer so that there are at least
$E_i=(c_1-c_i)\cdots (c_{i-1}-c_i)(c_{i+1}-c_i)\cdots (c_n-c_i) = \pm D_i^{-1}$
. Let M be a large integer so that there are at least
![]() $n-1$
distinct primes
$n-1$
distinct primes
![]() $q_1,\ldots ,q_{n-1}$
lying inside
$q_1,\ldots ,q_{n-1}$
lying inside
![]() $(M - \sqrt {M}, M)$
. Let
$(M - \sqrt {M}, M)$
. Let
![]() $c_n = M$
, and let
$c_n = M$
, and let
![]() $c_i = M - q_i$
for
$c_i = M - q_i$
for
![]() $i = 1,\ldots ,n-1$
. Then for any
$i = 1,\ldots ,n-1$
. Then for any
![]() $i,j=1,\ldots ,n-1$
with
$i,j=1,\ldots ,n-1$
with
![]() $j\neq i$
, we have
$j\neq i$
, we have
![]() $q_i\mid E_i$
and
$q_i\mid E_i$
and
![]() $q_i\nmid E_j$
. Note also that
$q_i\nmid E_j$
. Note also that
![]() $E_n = (-1)^{n-1}q_1\cdots q_{n-1}$
. For each
$E_n = (-1)^{n-1}q_1\cdots q_{n-1}$
. For each
![]() $i=1,\ldots ,n-1$
, let
$i=1,\ldots ,n-1$
, let
![]() $\sigma _i$
denote an element in the absolute Galois group
$\sigma _i$
denote an element in the absolute Galois group
![]() $G_{{\mathbb Q}[\sqrt {-1}]}$
that negates
$G_{{\mathbb Q}[\sqrt {-1}]}$
that negates
![]() $\sqrt {q_j}$
for all
$\sqrt {q_j}$
for all
![]() $j=1,\ldots ,n-1$
for which
$j=1,\ldots ,n-1$
for which
![]() $j\neq i$
and fixes all other square roots that appear (including
$j\neq i$
and fixes all other square roots that appear (including
![]() $\sqrt {q_i}$
). Since n is odd, we see that
$\sqrt {q_i}$
). Since n is odd, we see that
![]() $\sigma _i(d_j)=-d_j$
for all
$\sigma _i(d_j)=-d_j$
for all
![]() $j\neq i$
and
$j\neq i$
and
![]() $\sigma _i(d_i) = d_i$
. Hence,
$\sigma _i(d_i) = d_i$
. Hence,
That is, the absolute Galois group
![]() $G_{{\mathbb Q}[\sqrt {-1}]}$
acts transitively on the set
$G_{{\mathbb Q}[\sqrt {-1}]}$
acts transitively on the set
![]() $\{[d_1\colon \cdots \colon d_n]\mid d_i^2=D_i\}$
. Hence, it also acts transitively on the
$\{[d_1\colon \cdots \colon d_n]\mid d_i^2=D_i\}$
. Hence, it also acts transitively on the
![]() $2^{2g} Y$
’s defined in (4.2) as the
$2^{2g} Y$
’s defined in (4.2) as the
![]() $d_i$
’s vary and so also acts transitively on
$d_i$
’s vary and so also acts transitively on
![]() $P_1,\ldots ,P_{2^{2g}}$
. We may simply choose the integers
$P_1,\ldots ,P_{2^{2g}}$
. We may simply choose the integers
![]() $\alpha _i,\beta _i$
so that
$\alpha _i,\beta _i$
so that
![]() $Q_1,\ldots ,Q_{2^{2g}}$
are distinct. Let
$Q_1,\ldots ,Q_{2^{2g}}$
are distinct. Let
![]() $B'=\text {diag}(c_1,\ldots ,c_n)$
, and let
$B'=\text {diag}(c_1,\ldots ,c_n)$
, and let
![]() $B_0 = P^{-1}B'(P^{-1})^t\in W({\mathbb Q}[\sqrt {-1}])$
. Then
$B_0 = P^{-1}B'(P^{-1})^t\in W({\mathbb Q}[\sqrt {-1}])$
. Then
![]() $G_{{\mathbb Q}[\sqrt {-1}]}$
acts transitively on the
$G_{{\mathbb Q}[\sqrt {-1}]}$
acts transitively on the
![]() $2^{2g}$
distinct roots of
$2^{2g}$
distinct roots of
![]() $F(B_0,x)$
.
$F(B_0,x)$
.
Theorem 4.2. Suppose
![]() $n = 2g+2$
is even. Let
$n = 2g+2$
is even. Let
![]() $R = {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][c]/(\det (cA_0 - B))$
, and let K be its fraction field. Then there exists a polynomial
$R = {\mathbb Z}[\sqrt {-1}][b_{11},\ldots ,b_{nn}][c]/(\det (cA_0 - B))$
, and let K be its fraction field. Then there exists a polynomial
![]() $F(B,c,x)\in R[x]$
of degree
$F(B,c,x)\in R[x]$
of degree
![]() $2^{2g}$
that is irreducible in
$2^{2g}$
that is irreducible in
![]() $K[x]$
, such that for any
$K[x]$
, such that for any
![]() $B_0\in W({\mathbb Q})$
, if
$B_0\in W({\mathbb Q})$
, if
![]() $B_0$
is distinguished and
$B_0$
is distinguished and
![]() $c_0\in \bar {{\mathbb Q}}$
is any eigenvalue of
$c_0\in \bar {{\mathbb Q}}$
is any eigenvalue of
![]() $B_0$
, then
$B_0$
, then
![]() $F(B_0,c_0,x)\in {\mathbb Q}[\sqrt {-1}][c_0][x]$
has a root in
$F(B_0,c_0,x)\in {\mathbb Q}[\sqrt {-1}][c_0][x]$
has a root in
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Proof. Given
![]() $(B,c)$
, we proceed as before to orthogonally diagonalise
$(B,c)$
, we proceed as before to orthogonally diagonalise
![]() $B'=PBP^t$
into
$B'=PBP^t$
into
![]() $B'' = \text {diag}(c_1,\ldots ,c_{n-1},c)$
. Then we take
$B'' = \text {diag}(c_1,\ldots ,c_{n-1},c)$
. Then we take
![]() $B''' = B'' - cI_n = \text {diag}(c_1-c,\ldots ,c_{n-1}-c,0)$
and use the construction above in the odd degree case with
$B''' = B'' - cI_n = \text {diag}(c_1-c,\ldots ,c_{n-1}-c,0)$
and use the construction above in the odd degree case with
![]() $c_1,\ldots ,c_n$
replaced by
$c_1,\ldots ,c_n$
replaced by
![]() $c_1-c,\ldots ,c_{n-1}-c$
to obtain a polynomial whose coefficients are polynomials that are symmetric in
$c_1-c,\ldots ,c_{n-1}-c$
to obtain a polynomial whose coefficients are polynomials that are symmetric in
![]() $c_1 - c, \ldots , c_{n-1}-c$
. Note that
$c_1 - c, \ldots , c_{n-1}-c$
. Note that
![]() $(x-c_1)\cdots (x-c_{n-1}) = \det (xA_0-B)/(x-c)\in R[x]$
. Hence,
$(x-c_1)\cdots (x-c_{n-1}) = \det (xA_0-B)/(x-c)\in R[x]$
. Hence,
![]() $(x-(c_1-c))\cdots (x-(c_{n-1}-c))\in R[x]$
, and so any polynomial that is symmetric in
$(x-(c_1-c))\cdots (x-(c_{n-1}-c))\in R[x]$
, and so any polynomial that is symmetric in
![]() $c_1 - c, \ldots , c_{n-1}-c$
belongs to R.
$c_1 - c, \ldots , c_{n-1}-c$
belongs to R.
As an immediate consequence of Theorems 4.1 and 4.2, we may apply the quantitative Hilbert irreducibility theorem of Castillo and Dietmann [Reference Castillo and Dietmann9] to bound the number of distinguished elements in homogeneously expanding sets. Let
![]() $W({\mathbb Z})^{\mathrm {dist}}$
denote the set of distinguished elements in
$W({\mathbb Z})^{\mathrm {dist}}$
denote the set of distinguished elements in
![]() $W({\mathbb Z})$
. Then we have the following result.
$W({\mathbb Z})$
. Then we have the following result.
Corollary 4.3. Let
![]() ${\mathcal B}\subset W({\mathbb R})$
be a bounded open set. Let
${\mathcal B}\subset W({\mathbb R})$
be a bounded open set. Let
![]() $Y=(Y_{ij})$
be an
$Y=(Y_{ij})$
be an
![]() $n\times n$
matrix of positive real numbers. Let
$n\times n$
matrix of positive real numbers. Let
![]() $Y\cdot {\mathcal B}$
be the set obtained by scaling the
$Y\cdot {\mathcal B}$
be the set obtained by scaling the
![]() $(i,j)$
-entries of elements in
$(i,j)$
-entries of elements in
![]() ${\mathcal B}$
by
${\mathcal B}$
by
![]() $Y_{ij}$
. Then we have
$Y_{ij}$
. Then we have
 $$ \begin{align} \#\big\{Y\cdot {\mathcal B}\cap W({\mathbb Z})^{\mathrm{dist}}\big\}&= O_\epsilon\left( \frac{\prod Y_{ij}^{1+\epsilon}}{\min\big\{Y_{ij}^{1-1/2^{2g}}\big\}} \right). \end{align} $$
$$ \begin{align} \#\big\{Y\cdot {\mathcal B}\cap W({\mathbb Z})^{\mathrm{dist}}\big\}&= O_\epsilon\left( \frac{\prod Y_{ij}^{1+\epsilon}}{\min\big\{Y_{ij}^{1-1/2^{2g}}\big\}} \right). \end{align} $$
Proof. Define
![]() $F_1(B,x)$
to be
$F_1(B,x)$
to be
![]() $N_{{\mathbb Q}[\sqrt {-1}]/{\mathbb Q}}F(B,x)$
in the odd case and to be
$N_{{\mathbb Q}[\sqrt {-1}]/{\mathbb Q}}F(B,x)$
in the odd case and to be
![]() $N_{K/{\mathbb Q}(b_{11},\ldots ,b_{nn})}F(B,c,x)$
in the even case. Theorems 4.1 and 4.2 imply that if
$N_{K/{\mathbb Q}(b_{11},\ldots ,b_{nn})}F(B,c,x)$
in the even case. Theorems 4.1 and 4.2 imply that if
![]() $B_0\in W({\mathbb Q})$
is distinguished, then the Galois group of
$B_0\in W({\mathbb Q})$
is distinguished, then the Galois group of
![]() $F_1(B_0,x)$
has index at least
$F_1(B_0,x)$
has index at least
![]() $2^{2g}$
in the generic Galois group of
$2^{2g}$
in the generic Galois group of
![]() $F_1(B,x)$
. More precisely, they imply that every irreducible factor of
$F_1(B,x)$
. More precisely, they imply that every irreducible factor of
![]() $F_1(B,x)$
has degree at least
$F_1(B,x)$
has degree at least
![]() $2^{2g}$
, and that if
$2^{2g}$
, and that if
![]() $B_0$
is distinguished, then
$B_0$
is distinguished, then
![]() $F_1(B_0,x)$
has a rational root.
$F_1(B_0,x)$
has a rational root.
We wish to upper bound the number of
![]() $B_0\in W({\mathbb Z})$
, with
$B_0\in W({\mathbb Z})$
, with
![]() $b_{ij}<Y_{ij}$
, such that
$b_{ij}<Y_{ij}$
, such that
![]() $f(B_0,x)$
has a rational root in x for some irreducible factor
$f(B_0,x)$
has a rational root in x for some irreducible factor
![]() $f(B,x)$
of
$f(B,x)$
of
![]() $F_1(B,x)$
. When all the
$F_1(B,x)$
. When all the
![]() $Y_{ij}$
’s are the same, say Y, the required bound follows immediately from [Reference Castillo and Dietmann9, Theorem 1]. Indeed, when applied to
$Y_{ij}$
’s are the same, say Y, the required bound follows immediately from [Reference Castillo and Dietmann9, Theorem 1]. Indeed, when applied to
![]() $f(B,x)$
with generic Galois group
$f(B,x)$
with generic Galois group
![]() $G_f$
, [Reference Castillo and Dietmann9, Theorem 1] states that the number of
$G_f$
, [Reference Castillo and Dietmann9, Theorem 1] states that the number of
![]() $B_0\in W({\mathbb Z})$
with each
$B_0\in W({\mathbb Z})$
with each
![]() $|b_{ij}|<Y$
, such that the Galois group of
$|b_{ij}|<Y$
, such that the Galois group of
![]() $f(B_0,x)$
is
$f(B_0,x)$
is
![]() $K\subset G_f$
, is
$K\subset G_f$
, is
![]() $O(Y^{\mathrm {dim}(W)-1+|G_f/K|^{-1}+\epsilon })$
. Since
$O(Y^{\mathrm {dim}(W)-1+|G_f/K|^{-1}+\epsilon })$
. Since
![]() $B_0$
being distinguished implies that
$B_0$
being distinguished implies that
![]() $f(B_0,x)$
has a rational root for some irreducible factor
$f(B_0,x)$
has a rational root for some irreducible factor
![]() $f(B,x)$
of
$f(B,x)$
of
![]() $F(B,x)$
, and the degree of
$F(B,x)$
, and the degree of
![]() $f(B,x)$
is at least
$f(B,x)$
is at least
![]() $2^{2g}$
, we have
$2^{2g}$
, we have
![]() $|G_f/K|\geq 2^{2g}$
and the result follows.
$|G_f/K|\geq 2^{2g}$
and the result follows.
The proof of [Reference Castillo and Dietmann9, Theorem 1] in the case where we require
![]() $f(B_0,x)$
to have a rational root (as opposed to a general Galois subgroup
$f(B_0,x)$
to have a rational root (as opposed to a general Galois subgroup
![]() $K\subset G_f$
) is much simpler than the general case (as the construction of a polynomial, associated to
$K\subset G_f$
) is much simpler than the general case (as the construction of a polynomial, associated to
![]() $f(B_0,x)$
, having a rational root may be skipped in this case). We now describe how this proof also carries through without any change for general
$f(B_0,x)$
, having a rational root may be skipped in this case). We now describe how this proof also carries through without any change for general
![]() $Y_{ij}$
. First,
$Y_{ij}$
. First,
![]() $f(B,x)$
can be assumed to be monic in x by replacing
$f(B,x)$
can be assumed to be monic in x by replacing
![]() $f(B,x)=g_0(B)x^m+g_1(B)x^{m-1}+\cdots + g_m(x)$
by
$f(B,x)=g_0(B)x^m+g_1(B)x^{m-1}+\cdots + g_m(x)$
by
![]() $g_0(B)^{m-1}f(B,x/g_0(B))$
. In order to make this reduction, it is necessary to provide an upper bound for the number of
$g_0(B)^{m-1}f(B,x/g_0(B))$
. In order to make this reduction, it is necessary to provide an upper bound for the number of
![]() $B_0\in W({\mathbb Z})$
with
$B_0\in W({\mathbb Z})$
with
![]() $|b_{ij}|<Y_{ij}$
, such that
$|b_{ij}|<Y_{ij}$
, such that
![]() $g_0(B_0)=0$
. This number is clearly bounded by the right-hand side of (4.3), as a fibring argument readily shows. Specifically, we fibre over all but one of the coefficients, denoted by b. Fixing values for each
$g_0(B_0)=0$
. This number is clearly bounded by the right-hand side of (4.3), as a fibring argument readily shows. Specifically, we fibre over all but one of the coefficients, denoted by b. Fixing values for each
![]() $b_{ij}\neq b$
yields a polynomial
$b_{ij}\neq b$
yields a polynomial
![]() $g(b)=g_0(B)$
in one variable. If
$g(b)=g_0(B)$
in one variable. If
![]() $g(b)$
is not identically zero, then
$g(b)$
is not identically zero, then
![]() $g(b)=0$
has
$g(b)=0$
has
![]() $O(1)$
different solutions, yielding a sufficient saving. Meanwhile, the condition of
$O(1)$
different solutions, yielding a sufficient saving. Meanwhile, the condition of
![]() $g(b)$
being identically zero imposes one or more polynomial vanishing conditions on the coefficients
$g(b)$
being identically zero imposes one or more polynomial vanishing conditions on the coefficients
![]() $b_{ij}\neq b$
, and the number of such values of
$b_{ij}\neq b$
, and the number of such values of
![]() $b_{ij}$
also satisfies the required bound by induction.
$b_{ij}$
also satisfies the required bound by induction.
The result for monic polynomials is proved in [Reference Castillo and Dietmann9, Lemma 7] by fibring over all but one of the coefficients and then using induction. This proof (for the case when all the
![]() $Y_{ij}$
’s are the same) carries over without change for general
$Y_{ij}$
’s are the same) carries over without change for general
![]() $Y_{ij}$
, when the fibring is done over the variables
$Y_{ij}$
, when the fibring is done over the variables
![]() $b_{ij}$
for which the
$b_{ij}$
for which the
![]() $Y_{ij}$
are the smallest.
$Y_{ij}$
are the smallest.
5 Proof of the main result
In this section, we prove Theorem 1.5 and its analogue for monic integer polynomials having vanishing subleading coefficient. We then prove Theorems 1.6 and 1.2.
We begin by bounding the number of monic integer polynomials with bounded height belonging to
![]() ${\mathcal W}_m^{(1)}$
(respectively,
${\mathcal W}_m^{(1)}$
(respectively,
![]() ${\mathcal W}_m^{(2)})$
for some large m. To bound the number of elements in
${\mathcal W}_m^{(2)})$
for some large m. To bound the number of elements in
![]() $\cup _{m>M} {\mathcal W}_{m}^{(1)}$
, we have the following result:
$\cup _{m>M} {\mathcal W}_{m}^{(1)}$
, we have the following result:
Proposition 5.1. We have
 $$ \begin{align} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}_{m}^{(1)}:H(f)<H\}= O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{2/(n-1)-\epsilon}}\bigg)+O(H^{n(n+1)/2-1}). \end{align} $$
$$ \begin{align} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}_{m}^{(1)}:H(f)<H\}= O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{2/(n-1)-\epsilon}}\bigg)+O(H^{n(n+1)/2-1}). \end{align} $$
Proof. We begin by noting that the proofs of [Reference Bhargava4, Theorem 3.5 and Lemma 3.6] imply the bound
 $$ \begin{align} \#\bigcup_{\substack{m>M }}|\mu(m)|\{f\in {\mathcal W}_{m}^{(1)}:H(f)<H\}= O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{1-\epsilon}}\bigg)+O(H^{n(n+1)/2-1}). \end{align} $$
$$ \begin{align} \#\bigcup_{\substack{m>M }}|\mu(m)|\{f\in {\mathcal W}_{m}^{(1)}:H(f)<H\}= O_\epsilon\bigg(\frac{H^{n(n+1)/2+\epsilon}}{M^{1-\epsilon}}\bigg)+O(H^{n(n+1)/2-1}). \end{align} $$
Briefly, the proof is as follows: first, there exists a polynomial
![]() $P\in {\mathbb Z}[V_n]$
, belonging to the algebra generated by
$P\in {\mathbb Z}[V_n]$
, belonging to the algebra generated by
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta '$
, which does not involve the constant coefficient
$\Delta '$
, which does not involve the constant coefficient
![]() $a_n$
. Hence, we may consider P as a polynomial in
$a_n$
. Hence, we may consider P as a polynomial in
![]() $a_1,\ldots , a_{n-1}$
. Second, a bound of size
$a_1,\ldots , a_{n-1}$
. Second, a bound of size
![]() $O(H^{n(n+1)/2-n-1})$
is easily obtained on the number of possible values of
$O(H^{n(n+1)/2-n-1})$
is easily obtained on the number of possible values of
![]() $a=(a_1,\ldots ,a_{n-1})$
, of bounded height, for which
$a=(a_1,\ldots ,a_{n-1})$
, of bounded height, for which
![]() $P(a)=0$
. Third, we fibre over the
$P(a)=0$
. Third, we fibre over the
![]() $O(H^{n(n+1)/2-n})$
values of such a for which
$O(H^{n(n+1)/2-n})$
values of such a for which
![]() $P(a)\neq 0$
. For each such a, it is clear that
$P(a)\neq 0$
. For each such a, it is clear that
![]() $P(a)$
has at most
$P(a)$
has at most
![]() $O(H^\epsilon )$
different divisors. Since
$O(H^\epsilon )$
different divisors. Since
![]() $P(f)=P(a_1,\ldots ,a_{n-1})\equiv 0\pmod {m}$
for
$P(f)=P(a_1,\ldots ,a_{n-1})\equiv 0\pmod {m}$
for
![]() $f(x)=x^n+\sum _{i=1}^n a_{i}X^{n-i}\in {\mathcal W}_m$
, fixing a constrains the value of
$f(x)=x^n+\sum _{i=1}^n a_{i}X^{n-i}\in {\mathcal W}_m$
, fixing a constrains the value of
![]() $m>M$
to be one of these
$m>M$
to be one of these
![]() $O(H^\epsilon )$
divisors of
$O(H^\epsilon )$
divisors of
![]() $P(a)$
. Fourth, and finally, we consider
$P(a)$
. Fourth, and finally, we consider
![]() $\Delta $
to be a polynomial
$\Delta $
to be a polynomial
![]() $\Delta _a(a_n)$
in
$\Delta _a(a_n)$
in
![]() $a_n$
. We then note that the condition
$a_n$
. We then note that the condition
![]() $m\mid \Delta (f)=\Delta _a(a_n)$
implies that there are at most
$m\mid \Delta (f)=\Delta _a(a_n)$
implies that there are at most
![]() $O((H^n/m^{1-\epsilon })+1)=O((H^n/M^{1-\epsilon })+1)$
choices for
$O((H^n/m^{1-\epsilon })+1)=O((H^n/M^{1-\epsilon })+1)$
choices for
![]() $a_n$
, concluding the proof of (5.2).
$a_n$
, concluding the proof of (5.2).
It is precisely this last step which breaks down when m is not required to be squarefree. We note that
![]() $\Delta _a(a_n)$
is a polynomial of degree
$\Delta _a(a_n)$
is a polynomial of degree
![]() $n-1$
in
$n-1$
in
![]() $a_n$
, whose leading coefficient
$a_n$
, whose leading coefficient
![]() $(-1)^{n(n-1)/2} n^{n-1}$
does not depend on a. Suppose
$(-1)^{n(n-1)/2} n^{n-1}$
does not depend on a. Suppose
![]() $p^k\parallel m$
for some prime p and some fixed
$p^k\parallel m$
for some prime p and some fixed
![]() $m\mid P(a)$
. Let
$m\mid P(a)$
. Let
![]() $\ell \ll _n 1$
be a nonnegative integer, such that
$\ell \ll _n 1$
be a nonnegative integer, such that
![]() $g(a_n) = \Delta _a(a_n)/p^\ell \in {\mathbb Z}[x]$
and at least one of its coefficients is not divisible by p. The condition
$g(a_n) = \Delta _a(a_n)/p^\ell \in {\mathbb Z}[x]$
and at least one of its coefficients is not divisible by p. The condition
![]() $m^2\mid \Delta (f)$
now becomes
$m^2\mid \Delta (f)$
now becomes
![]() $p^{2k-\ell }\mid g(a_n)$
for every prime divisor p of m. Let
$p^{2k-\ell }\mid g(a_n)$
for every prime divisor p of m. Let
![]() $\delta = \lceil \frac {2k-\ell }{n-1}\rceil $
, and let
$\delta = \lceil \frac {2k-\ell }{n-1}\rceil $
, and let
![]() $g(x) = f_1(x)\cdots f_j(x)$
be a factorisation in
$g(x) = f_1(x)\cdots f_j(x)$
be a factorisation in
![]() $({\mathbb Z}/p^\delta {\mathbb Z})[x]$
, where j is maximal. Since the reduction
$({\mathbb Z}/p^\delta {\mathbb Z})[x]$
, where j is maximal. Since the reduction
![]() $\bar {g}(x)\in {\mathbb F}_p[x]$
of
$\bar {g}(x)\in {\mathbb F}_p[x]$
of
![]() $g(x)$
modulo p is a nonzero polynomial of degree at most
$g(x)$
modulo p is a nonzero polynomial of degree at most
![]() $n-1$
, we have
$n-1$
, we have
![]() $\bar {g} = \bar {f_1}\cdots \bar {f_j}$
, and so
$\bar {g} = \bar {f_1}\cdots \bar {f_j}$
, and so
![]() $j\leq n-1.$
In order for
$j\leq n-1.$
In order for
![]() $p^{2k-\ell }\mid g(a_n)$
, we then must have
$p^{2k-\ell }\mid g(a_n)$
, we then must have
![]() $p^\delta \mid f_i(a_n)$
for some
$p^\delta \mid f_i(a_n)$
for some
![]() $i = 1,\ldots ,j$
. This implies that
$i = 1,\ldots ,j$
. This implies that
![]() $(x-a_n)\mid f_i(x)$
in
$(x-a_n)\mid f_i(x)$
in
![]() $({\mathbb Z}/p^\delta {\mathbb Z})[x]$
, and so by maximality of j, we see that
$({\mathbb Z}/p^\delta {\mathbb Z})[x]$
, and so by maximality of j, we see that
![]() $f_i(x)$
is linear. Hence, the density of integers
$f_i(x)$
is linear. Hence, the density of integers
![]() $a_n$
, such that
$a_n$
, such that
![]() $p^{2k-\ell }\mid g(a_n)$
is at most
$p^{2k-\ell }\mid g(a_n)$
is at most
![]() $(n-1)/p^\delta .$
Multiplying over all prime divisors p of m gives that the density of integers
$(n-1)/p^\delta .$
Multiplying over all prime divisors p of m gives that the density of integers
![]() $a_n$
, such that
$a_n$
, such that
![]() $m^2\mid \Delta _a(a_n)$
is
$m^2\mid \Delta _a(a_n)$
is
![]() $O(1/m^{2/(n-1)-\epsilon })$
. Combining with the proof of [Reference Bhargava4, Theorem 3.5 and Lemma 3.6] recalled above gives (5.1).
$O(1/m^{2/(n-1)-\epsilon })$
. Combining with the proof of [Reference Bhargava4, Theorem 3.5 and Lemma 3.6] recalled above gives (5.1).
We are ready to prove Theorem 1.5.
Proof of Theorem 1.5
To bound the number of elements in
![]() $\cup _{m>M} {\mathcal W}_{m}^{(2)}$
, we recall the setup of [Reference Bhargava, Shankar and Wang7]. The proofs of [Reference Bhargava, Shankar and Wang7, Theorems 2.3 and 3.2] imply that we have a map
$\cup _{m>M} {\mathcal W}_{m}^{(2)}$
, we recall the setup of [Reference Bhargava, Shankar and Wang7]. The proofs of [Reference Bhargava, Shankar and Wang7, Theorems 2.3 and 3.2] imply that we have a map
![]() $\sigma _m:{\mathcal W}_{m}^{(2)}\to \frac 14 W({\mathbb Z})$
, injecting into the set of distinguished elements, such that the resolvent of
$\sigma _m:{\mathcal W}_{m}^{(2)}\to \frac 14 W({\mathbb Z})$
, injecting into the set of distinguished elements, such that the resolvent of
![]() $\sigma _m(f)$
is f and
$\sigma _m(f)$
is f and
![]() $Q(\sigma _m(f))=m$
. Here, Q is an invariant defined on the set of distinguished elements of
$Q(\sigma _m(f))=m$
. Here, Q is an invariant defined on the set of distinguished elements of
![]() $W({\mathbb Z})$
, given explicitly in [Reference Bhargava, Shankar and Wang7, §§2.1 and 3.1]. To bound the number of elements in
$W({\mathbb Z})$
, given explicitly in [Reference Bhargava, Shankar and Wang7, §§2.1 and 3.1]. To bound the number of elements in
![]() $\cup _{m>M} {\mathcal W}_{m}^{(2)}$
having height less than H, it thus suffices to bound the number of
$\cup _{m>M} {\mathcal W}_{m}^{(2)}$
having height less than H, it thus suffices to bound the number of
![]() $G({\mathbb Z})$
-orbits on distinguished elements of
$G({\mathbb Z})$
-orbits on distinguished elements of
![]() $W({\mathbb Z})$
having height less than H and Q-invariant larger than M. This is precisely what is carried out via geometry-of-numbers arguments in [Reference Bhargava, Shankar and Wang7, §2 and 3]. Moreover, using Corollary 4.3 instead of the Selberg sieve in the proofs of [Reference Bhargava, Shankar and Wang7, Propositions 2.6 and 3.5] improves the error terms there to
$W({\mathbb Z})$
having height less than H and Q-invariant larger than M. This is precisely what is carried out via geometry-of-numbers arguments in [Reference Bhargava, Shankar and Wang7, §2 and 3]. Moreover, using Corollary 4.3 instead of the Selberg sieve in the proofs of [Reference Bhargava, Shankar and Wang7, Propositions 2.6 and 3.5] improves the error terms there to
![]() $O_\epsilon (H^{\mathrm {dim}(W)-1+1/2^{2g}+\epsilon })$
. We thus obtain the following bound:
$O_\epsilon (H^{\mathrm {dim}(W)-1+1/2^{2g}+\epsilon })$
. We thus obtain the following bound:
We note that (5.3) is a strengthening of [Reference Bhargava, Shankar and Wang7, Theorem 1.5(b)]. Optimising by taking
![]() $\alpha = (n-1)/(n+3)$
and
$\alpha = (n-1)/(n+3)$
and
![]() $\beta = 2/(n+3)$
in Proposition 3.2 gives Theorem 1.5.
$\beta = 2/(n+3)$
in Proposition 3.2 gives Theorem 1.5.
We now deduce Theorem 1.6 from 1.5.
Proof of Theorem 1.6
Applying an inclusion-exclusion sieve, we obtain
We break up the sum over m into three ranges, namely, the large range consisting of
![]() $m\geq H^{n/2}$
, the middle range consisting of
$m\geq H^{n/2}$
, the middle range consisting of
![]() $H\leq m< H^{n/2}$
and the small range consisting of
$H\leq m< H^{n/2}$
and the small range consisting of
![]() $m<H$
. We will obtain precise estimates for the sum of m over the small range and prove that the sum over m in the middle and large ranges are negligible, where we say that a number is negligible if it is
$m<H$
. We will obtain precise estimates for the sum of m over the small range and prove that the sum over m in the middle and large ranges are negligible, where we say that a number is negligible if it is
![]() $O_\epsilon (H^{n(n+1)/2-1+1/2^{2g}+\epsilon })$
.
$O_\epsilon (H^{n(n+1)/2-1+1/2^{2g}+\epsilon })$
.
First, note that Theorem 1.5 implies the bound
Therefore, the sum over the large range is negligible.
Next we consider the middle range. That is, we sum the right-hand side of (5.4) over m in the range
![]() $H<m\leq H^{n/2}$
and prove that the sum is
$H<m\leq H^{n/2}$
and prove that the sum is
![]() $O_\epsilon (H^{n(n+1)/2-1+\epsilon })$
. We fibre over integer tuples
$O_\epsilon (H^{n(n+1)/2-1+\epsilon })$
. We fibre over integer tuples
![]() $a=(a_1,\ldots ,a_{n-1})$
. For any integer tuple a, let
$a=(a_1,\ldots ,a_{n-1})$
. For any integer tuple a, let
![]() $\Delta _a(a_n)$
denote as above the discriminant of
$\Delta _a(a_n)$
denote as above the discriminant of
![]() $x^n + a_1x^{n-1} + \cdots + a_n$
and let
$x^n + a_1x^{n-1} + \cdots + a_n$
and let
![]() $\theta _a(m)$
denote the density of integers
$\theta _a(m)$
denote the density of integers
![]() $a_n$
, such that
$a_n$
, such that
![]() $m^2\mid \Delta _a(a_n).$
Let B denote the set of integer tuples
$m^2\mid \Delta _a(a_n).$
Let B denote the set of integer tuples
![]() $a=(a_1,\ldots ,a_{n-1})$
, such that
$a=(a_1,\ldots ,a_{n-1})$
, such that
![]() $|a_i|<H^i$
for
$|a_i|<H^i$
for
![]() $i=1,\ldots ,n-1$
. Then we have
$i=1,\ldots ,n-1$
. Then we have
Since
![]() $\#B = O(H^{n(n+1)/2 - n})$
, we see that the sum of the
$\#B = O(H^{n(n+1)/2 - n})$
, we see that the sum of the
![]() $O(1)$
term is negligible.
$O(1)$
term is negligible.
Now the discriminant
![]() $\Delta (\Delta _a)$
of
$\Delta (\Delta _a)$
of
![]() $\Delta _a(a_n)$
is a polynomial in
$\Delta _a(a_n)$
is a polynomial in
![]() $a_1,\ldots ,a_{n-1}$
. We claim that
$a_1,\ldots ,a_{n-1}$
. We claim that
![]() $\Delta (\Delta _a)$
has a term involving only
$\Delta (\Delta _a)$
has a term involving only
![]() $a_{n-1}$
. Indeed, when
$a_{n-1}$
. Indeed, when
![]() $a_1=\cdots =a_{n-2}=0$
, we have
$a_1=\cdots =a_{n-2}=0$
, we have
and so
for some nonzero constant
![]() $C_n$
depending only on n. As a consequence, given any values for
$C_n$
depending only on n. As a consequence, given any values for
![]() $a_1,\ldots ,a_{n-2}$
,
$a_1,\ldots ,a_{n-2}$
,
![]() $\Delta (\Delta _a)$
will be a nonzero polynomial in
$\Delta (\Delta _a)$
will be a nonzero polynomial in
![]() $a_{n-1}$
. Hence, we have
$a_{n-1}$
. Hence, we have
Hence, the contribution to the right-hand side of (5.6) over
![]() $a\in B$
with
$a\in B$
with
![]() $\Delta (\Delta _a) = 0$
is negligible.
$\Delta (\Delta _a) = 0$
is negligible.
Suppose now
![]() $a\in B$
with
$a\in B$
with
![]() $\Delta (\Delta _a)\neq 0$
. Take any squarefree m with
$\Delta (\Delta _a)\neq 0$
. Take any squarefree m with
![]() $H<m\leq H^{n/2}$
. Let
$H<m\leq H^{n/2}$
. Let
![]() $d = \gcd (\Delta (\Delta _a),m)$
, and let
$d = \gcd (\Delta (\Delta _a),m)$
, and let
![]() $m_1 = m/d$
. For any prime
$m_1 = m/d$
. For any prime
![]() $p\mid d$
and
$p\mid d$
and
![]() $p\nmid n$
, the polynomial
$p\nmid n$
, the polynomial
![]() $\Delta _a(a_n)$
mod p is a nonzero polynomial (since its leading coefficient is nonzero) with a repeated factor, in which case,
$\Delta _a(a_n)$
mod p is a nonzero polynomial (since its leading coefficient is nonzero) with a repeated factor, in which case,
![]() $\theta _a(p) = O(1/p).$
For any prime
$\theta _a(p) = O(1/p).$
For any prime
![]() $p\mid m_1$
and
$p\mid m_1$
and
![]() $p\nmid n$
, the polynomial
$p\nmid n$
, the polynomial
![]() $\Delta _a(a_n)$
mod p is a nonzero polynomial without a repeated factor, in which case,
$\Delta _a(a_n)$
mod p is a nonzero polynomial without a repeated factor, in which case,
![]() $\theta _a(p) = O(1/p^2).$
Hence, we have
$\theta _a(p) = O(1/p^2).$
Hence, we have
![]() $\theta _a(m) = O(1/(dm_1^{2-\epsilon })),$
where we absorb any common divisors of d and n, or of
$\theta _a(m) = O(1/(dm_1^{2-\epsilon })),$
where we absorb any common divisors of d and n, or of
![]() $m_1$
and n, into the implied constant. Denoting by
$m_1$
and n, into the implied constant. Denoting by
![]() $\sideset {}{'}\sum $
a sum over squarefree numbers, we have
$\sideset {}{'}\sum $
a sum over squarefree numbers, we have
 $$ \begin{align*} \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}} \sideset{}{'}\sum_{H<m\leq H^{n/2}} \theta_a(m) &\ll_\epsilon \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}}\bigg( \sideset{}{'}\sum_{\substack{1\leq d\leq H\\ d\mid\Delta(\Delta_a)}} \sideset{}{'}\sum_{\frac{H}{d}<m_1\leq \frac{H^{n/2}}{d}}\frac{1}{dm_1^{2-\epsilon}}+\sideset{}{'}\sum_{\substack{H< d\leq H^{n/2}\\ d\mid\Delta(\Delta_a)}} \sideset{}{'}\sum_{1<m_1\leq \frac{H^{n/2}}{d}}\frac{1}{dm_1^{2-\epsilon}}\bigg)\\ &\ll_\epsilon \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}} \sideset{}{'}\sum_{\substack{1\leq d\leq H^{n/2}\\ d\mid\Delta(\Delta_a)}} \frac{1}{H^{1-\epsilon}}\\ &\ll_\epsilon H^{n(n+1)/2-n -1+\epsilon}, \end{align*} $$
$$ \begin{align*} \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}} \sideset{}{'}\sum_{H<m\leq H^{n/2}} \theta_a(m) &\ll_\epsilon \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}}\bigg( \sideset{}{'}\sum_{\substack{1\leq d\leq H\\ d\mid\Delta(\Delta_a)}} \sideset{}{'}\sum_{\frac{H}{d}<m_1\leq \frac{H^{n/2}}{d}}\frac{1}{dm_1^{2-\epsilon}}+\sideset{}{'}\sum_{\substack{H< d\leq H^{n/2}\\ d\mid\Delta(\Delta_a)}} \sideset{}{'}\sum_{1<m_1\leq \frac{H^{n/2}}{d}}\frac{1}{dm_1^{2-\epsilon}}\bigg)\\ &\ll_\epsilon \sum_{\substack{a\in B\\ \Delta(\Delta_a)\neq 0}} \sideset{}{'}\sum_{\substack{1\leq d\leq H^{n/2}\\ d\mid\Delta(\Delta_a)}} \frac{1}{H^{1-\epsilon}}\\ &\ll_\epsilon H^{n(n+1)/2-n -1+\epsilon}, \end{align*} $$
where the last bound follows because the number of divisors of the nonzero integer
![]() $\Delta (\Delta _a)$
with each
$\Delta (\Delta _a)$
with each
![]() $a_i$
bounded by some fixed power of H is
$a_i$
bounded by some fixed power of H is
![]() $O_\epsilon (H^\epsilon )$
. Therefore, we have proved that
$O_\epsilon (H^\epsilon )$
. Therefore, we have proved that
It remains to consider the small range
![]() $1\leq m \leq H$
. For this range, note that
$1\leq m \leq H$
. For this range, note that
![]() $m^2\leq H^2$
is less than the range of
$m^2\leq H^2$
is less than the range of
![]() $a_2$
, and so we fibre over
$a_2$
, and so we fibre over
![]() $a_1$
only. Denote the density of
$a_1$
only. Denote the density of
![]() ${\mathcal W}_m$
in
${\mathcal W}_m$
in
![]() $V_n({\mathbb Z})$
by
$V_n({\mathbb Z})$
by
![]() $\theta (m)$
. When
$\theta (m)$
. When
![]() $m=p$
is a prime, we have
$m=p$
is a prime, we have
![]() $\theta (p) = O(1/p^2)$
. When m is squarefree in general, we have
$\theta (p) = O(1/p^2)$
. When m is squarefree in general, we have
![]() $\theta (m) = O_\epsilon (1/m^{2-\epsilon }).$
For any integer
$\theta (m) = O_\epsilon (1/m^{2-\epsilon }).$
For any integer
![]() $a_1$
, let
$a_1$
, let
![]() $V_n(a_1,{\mathbb Z})$
denote the set of monic polynomials of degree n whose
$V_n(a_1,{\mathbb Z})$
denote the set of monic polynomials of degree n whose
![]() $x^{n-1}$
-coefficient is
$x^{n-1}$
-coefficient is
![]() $a_1$
and let
$a_1$
and let
![]() $\theta (a_1,m)$
denote the density of
$\theta (a_1,m)$
denote the density of
![]() ${\mathcal W}_m\cap V_n(a_1,{\mathbb Z})$
in
${\mathcal W}_m\cap V_n(a_1,{\mathbb Z})$
in
![]() $V_n(a_1,{\mathbb Z})$
. When m is coprime to n, we simply have
$V_n(a_1,{\mathbb Z})$
. When m is coprime to n, we simply have
![]() $\theta (a_1,m) = \theta (m).$
$\theta (a_1,m) = \theta (m).$
We fibre over
![]() $a_1$
and break the regions for
$a_1$
and break the regions for
![]() $a_2,\ldots ,a_n$
into intervals of length
$a_2,\ldots ,a_n$
into intervals of length
![]() $m^2$
to obtain
$m^2$
to obtain
 $$ \begin{align*} &\sum_{1\leq m\leq H}\mu(m)\#\{f\in {\mathcal W}_m:H(f)<H\}\\ &=\displaystyle\sum_{1\leq m\leq H}\mu(m)\sum_{|a_1|<H}(\theta(a_1,m)2^{n-1}H^{n(n+1)/2-1}+O(H^{n(n+1)/2-3})) \\ &=2^{n-1}H^{n(n+1)/2-1}\sum_{d\mid n}\sum_{\substack{1\leq m_1\leq H/d\\ \gcd(m_1,n) = 1}} \mu(d)\mu(m_1) \sum_{|a_1| < H} \theta(a_1,d)\theta(a_1,m_1) + O(H^{n(n+1)/2-1})\\ &= 2^{n-1}H^{n(n+1)/2-1}\sum_{\substack{1\leq m_1\leq H/d\\ \gcd(m_1,n) = 1}}\mu(m_1)\theta(m_1)\sum_{d\mid n}\mu(d)\sum_{|a_1| < H}\theta(a_1,d)+ O(H^{n(n+1)/2-1}). \end{align*} $$
$$ \begin{align*} &\sum_{1\leq m\leq H}\mu(m)\#\{f\in {\mathcal W}_m:H(f)<H\}\\ &=\displaystyle\sum_{1\leq m\leq H}\mu(m)\sum_{|a_1|<H}(\theta(a_1,m)2^{n-1}H^{n(n+1)/2-1}+O(H^{n(n+1)/2-3})) \\ &=2^{n-1}H^{n(n+1)/2-1}\sum_{d\mid n}\sum_{\substack{1\leq m_1\leq H/d\\ \gcd(m_1,n) = 1}} \mu(d)\mu(m_1) \sum_{|a_1| < H} \theta(a_1,d)\theta(a_1,m_1) + O(H^{n(n+1)/2-1})\\ &= 2^{n-1}H^{n(n+1)/2-1}\sum_{\substack{1\leq m_1\leq H/d\\ \gcd(m_1,n) = 1}}\mu(m_1)\theta(m_1)\sum_{d\mid n}\mu(d)\sum_{|a_1| < H}\theta(a_1,d)+ O(H^{n(n+1)/2-1}). \end{align*} $$
For any squarefree
![]() $d\mid n$
, we also have
$d\mid n$
, we also have
as both sides count monic polynomials of degree n with height bounded by H having discriminant divisible by
![]() $d^2$
. Hence,
$d^2$
. Hence,
and, thus,
since the sum of
![]() $O(1)$
over
$O(1)$
over
![]() $d\mid n$
is independent of H. Finally, combined with
$d\mid n$
is independent of H. Finally, combined with
 $$ \begin{align*}\sum_{\substack{1\leq m_1<H/d\\ \gcd(m_1,n) = 1}}\mu(m_1)\theta(m_1) \ll_\epsilon \sum_{m_1\geq1}\frac{1}{m_1^{2-\epsilon}} = O(1)\end{align*} $$
$$ \begin{align*}\sum_{\substack{1\leq m_1<H/d\\ \gcd(m_1,n) = 1}}\mu(m_1)\theta(m_1) \ll_\epsilon \sum_{m_1\geq1}\frac{1}{m_1^{2-\epsilon}} = O(1)\end{align*} $$
and
 $$ \begin{align*}\sum_{1\leq m\leq H}\mu(m)\theta(m) = \sum_{m\geq1}\mu(m)\theta(m) - \sum_{m>H}\mu(m)\theta(m) = \lambda_n - O_\epsilon(\sum_{m>H}\frac{1}{m^{2-\epsilon}}) = \lambda_n - O_\epsilon(\frac{1}{H^{1-\epsilon}}),\end{align*} $$
$$ \begin{align*}\sum_{1\leq m\leq H}\mu(m)\theta(m) = \sum_{m\geq1}\mu(m)\theta(m) - \sum_{m>H}\mu(m)\theta(m) = \lambda_n - O_\epsilon(\sum_{m>H}\frac{1}{m^{2-\epsilon}}) = \lambda_n - O_\epsilon(\frac{1}{H^{1-\epsilon}}),\end{align*} $$
we have
The first estimate of Theorem 1.6 now follows from (5.4), (5.5), (5.7) and (5.8). The second estimate follows similarly.
Next we deduce the analogue of Theorem 1.5 for polynomials with vanishing subleading coefficient.
Theorem 5.2. Let
![]() ${\mathcal W}_m^{\circ }$
denote the set of elements in
${\mathcal W}_m^{\circ }$
denote the set of elements in
![]() ${\mathcal W}_m$
that have vanishing subleading coefficient. Then
${\mathcal W}_m$
that have vanishing subleading coefficient. Then
 $$ \begin{align} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}^{\circ}_{m}:H(f)<H\}\ll_{n,\epsilon} \frac{H^{(n-1)(n+2)/2+\epsilon}}{{M^{2/(n+3)-\epsilon}}}+H^{(n-1)(n+2)/2-1+1/2^{2g}+\epsilon}. \end{align} $$
$$ \begin{align} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}^{\circ}_{m}:H(f)<H\}\ll_{n,\epsilon} \frac{H^{(n-1)(n+2)/2+\epsilon}}{{M^{2/(n+3)-\epsilon}}}+H^{(n-1)(n+2)/2-1+1/2^{2g}+\epsilon}. \end{align} $$
Proof. For an integer k, the transformation
![]() $f(x)\mapsto f(x+k)$
does not change membership in
$f(x)\mapsto f(x+k)$
does not change membership in
![]() ${\mathcal W}_m$
and changes the height of f by at most
${\mathcal W}_m$
and changes the height of f by at most
![]() $O(|k|)$
. Hence, the set of elements in
$O(|k|)$
. Hence, the set of elements in
![]() ${\mathcal W}_m$
having vanishing subleading coefficient and height
${\mathcal W}_m$
having vanishing subleading coefficient and height
![]() $<H$
are each equivalent (under some transformation
$<H$
are each equivalent (under some transformation
![]() $f(x)\mapsto f(x+k)$
) to
$f(x)\mapsto f(x+k)$
) to
![]() $\gg H$
elements in
$\gg H$
elements in
![]() ${\mathcal W}_m$
having height
${\mathcal W}_m$
having height
![]() $\ll H$
. Therefore,
$\ll H$
. Therefore,
 $$ \begin{align*} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}^{\circ}_{m}:H(f)<H\}\ll_n \frac{1}{H}\#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}_{m}:H(f)<H\}. \end{align*} $$
$$ \begin{align*} \#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}^{\circ}_{m}:H(f)<H\}\ll_n \frac{1}{H}\#\bigcup_{\substack{m>M }}\{f\in {\mathcal W}_{m}:H(f)<H\}. \end{align*} $$
The result now follows from Theorem 1.5.
We are now ready to prove Theorem 1.2.
Proof of Theorem 1.2
Let
![]() $N_n^{\mathrm {prim}}(X)$
denote the number of primitive number fields of degree n having absolute discriminant less than X. As explained in the Introduction, the set of primitive number fields with absolute discriminant less than X injects into the set of integer monic polynomials of degree n with vanishing subleading coefficient and height
$N_n^{\mathrm {prim}}(X)$
denote the number of primitive number fields of degree n having absolute discriminant less than X. As explained in the Introduction, the set of primitive number fields with absolute discriminant less than X injects into the set of integer monic polynomials of degree n with vanishing subleading coefficient and height
![]() $\ll X^{1/(2n-2)}$
. Let
$\ll X^{1/(2n-2)}$
. Let
![]() $S_X$
denote the image of this injection. Choose
$S_X$
denote the image of this injection. Choose
![]() $\kappa =n-1$
. By Proposition 2.1, it follows that away from a set
$\kappa =n-1$
. By Proposition 2.1, it follows that away from a set
![]() $S_X'$
of size
$S_X'$
of size
![]() $O(X^{\frac {n+2}{4}-\frac {1}{2n-2}})$
, every element in S has absolute discriminant
$O(X^{\frac {n+2}{4}-\frac {1}{2n-2}})$
, every element in S has absolute discriminant
![]() $\gg X^{\frac {n-1}{2}}$
. Since the absolute discriminant of the field corresponding to an element in
$\gg X^{\frac {n-1}{2}}$
. Since the absolute discriminant of the field corresponding to an element in
![]() $S_X$
is less than X by definition, the absolute discriminant of any element in
$S_X$
is less than X by definition, the absolute discriminant of any element in
![]() $S_X\backslash S_X'$
is divisible by
$S_X\backslash S_X'$
is divisible by
![]() $m^2$
for some
$m^2$
for some
![]() $m\gg X^{\frac {n-3}{4}}$
. By Theorem 5.2, we thus deduce that
$m\gg X^{\frac {n-3}{4}}$
. By Theorem 5.2, we thus deduce that
 $$ \begin{align*} \begin{array}{rcl} N_n^{\mathrm{prim}}(X)&\leq& \#S_X\;\;=\;\;\#S_X'+\#(S_X\backslash S_X') \\[.2in]&\ll_\epsilon&\displaystyle X^{\frac{n+2}{4}-\frac{1}{2n-2}}+ \frac{X^{\frac{n+2}{4}+\epsilon}}{X^{\frac{n-3}{2(n+3)}}}+X^{\frac{n+2}{4}-\frac{1}{2n-2}+\frac{1}{2^{2g}(2n-2)}+\epsilon}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rcl} N_n^{\mathrm{prim}}(X)&\leq& \#S_X\;\;=\;\;\#S_X'+\#(S_X\backslash S_X') \\[.2in]&\ll_\epsilon&\displaystyle X^{\frac{n+2}{4}-\frac{1}{2n-2}}+ \frac{X^{\frac{n+2}{4}+\epsilon}}{X^{\frac{n-3}{2(n+3)}}}+X^{\frac{n+2}{4}-\frac{1}{2n-2}+\frac{1}{2^{2g}(2n-2)}+\epsilon}. \end{array} \end{align*} $$
Since
![]() $\frac {n-3}{2(n+3)}\geq \frac {1}{2n-2}$
for
$\frac {n-3}{2(n+3)}\geq \frac {1}{2n-2}$
for
![]() $n\geq 6$
, we have proved the version of Theorem 1.2 where
$n\geq 6$
, we have proved the version of Theorem 1.2 where
![]() $N_n(X)$
is replaced by
$N_n(X)$
is replaced by
![]() $N_n^{\mathrm {prim}}(X)$
.
$N_n^{\mathrm {prim}}(X)$
.
Finally, we note that the bound [Reference Schmidt14, Equation (1.2)] with
![]() $L={\mathbb Q}$
implies that the number of imprimitive number fields of degree n with absolute discriminant less than X is at most
$L={\mathbb Q}$
implies that the number of imprimitive number fields of degree n with absolute discriminant less than X is at most
![]() $O(X^{\frac {n}{8}+\frac {1}{2}})$
. This completes the proof of Theorem 1.2.
$O(X^{\frac {n}{8}+\frac {1}{2}})$
. This completes the proof of Theorem 1.2.
Acknowledgements
The first-named author was supported by a Simons Investigator Grant and NSF Grant DMS-1001828. The second-named author was supported by an NSERC Discovery Grant and Sloan Research Fellowship. The third-named author was supported by an NSERC Discovery Grant. We are very grateful to Ashvin Swaminathan and Sameera Vemulapalli for helpful conversations and comments on an earlier version of this manuscript. We thank the referee for many helpful comments and, in particular, for pointing out an issue in the previous proof of what is now Proposition 5.1. We also thank Theresa Anderson, Ayla Gafni, Kevin Hughes, Robert Lemke Oliver, David Lowry-Duda, Frank Thorne, Jiuya Wang and Ruixiang Zhang for sharing with us their recent preprint [Reference Anderson, Gafni and Hughes1].
Conflicts of Interest
The authors have no conflicts of interest to declare.