 $\mathcal {L}$-OPERATOR ON CONFORMAL SOLITONS AND THEIR APPLICATIONS
$\mathcal {L}$-OPERATOR ON CONFORMAL SOLITONS AND THEIR APPLICATIONS
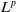 $L^p$ harmonic 1-forms on hypersurfaces with finite index
$L^p$ harmonic 1-forms on hypersurfaces with finite index
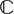 ${\mathbb C}$P2 AND
${\mathbb C}$P2 AND 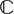 ${\mathbb C}$H2 WITH TWO DISTINCT PRINCIPAL CURVATURES
${\mathbb C}$H2 WITH TWO DISTINCT PRINCIPAL CURVATURES