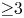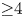1. Introduction
An isoparametric family of hypersurfaces is a decomposition of a Riemannian manifold into equidistant hypersurfaces of constant mean curvature and possibly one or two focal submanifolds with codimension greater than one. An isoparametric family is called homogeneous if it is the orbit foliation of an isometric action. In this article we provide a construction method of isoparametric hypersurfaces from where the next result follows.
Theorem 1 Each symmetric space ![]() $M$ of non-compact type and rank at least three admits inhomogeneous isoparametric families of hypersurfaces with non-austere focal submanifolds. If the rank is greater than or equal to four, there exist uncountably many such examples, up to congruence.
$M$ of non-compact type and rank at least three admits inhomogeneous isoparametric families of hypersurfaces with non-austere focal submanifolds. If the rank is greater than or equal to four, there exist uncountably many such examples, up to congruence.
We emphasize three novel and surprising features of this result.
First, among the symmetric spaces of non-compact type, only those in the very special class of ![]() $(BC_r)$ type (namely, those with non-reduced root system) were known to admit inhomogeneous isoparametric hypersurfaces [Reference Díaz-Ramos and Domínguez-VázquezDD13, Reference Domínguez-VázquezDom15, Reference Díaz-Ramos, Domínguez-Vázquez and Rodríguez-VázquezDDR21]. In this paper we construct examples in symmetric spaces of any type and rank at least three.
$(BC_r)$ type (namely, those with non-reduced root system) were known to admit inhomogeneous isoparametric hypersurfaces [Reference Díaz-Ramos and Domínguez-VázquezDD13, Reference Domínguez-VázquezDom15, Reference Díaz-Ramos, Domínguez-Vázquez and Rodríguez-VázquezDDR21]. In this paper we construct examples in symmetric spaces of any type and rank at least three.
Second, Theorem A provides the first isoparametric hypersurfaces which are known to have a non-austere focal submanifold in any Riemannian manifold. We recall that a submanifold is said to be austere if its multiset of principal curvatures is invariant under change of sign [Reference Harvey and LawsonHL82]. In particular, austere submanifolds are minimal. The focal submanifolds of an isoparametric family of hypersurfaces are always minimal [Reference Ge and TangGT14], and Theorem A shows that they do not need to be austere. We highlight the contrast with homogeneous hypersurfaces, as singular orbits of cohomogeneity-one actions are always austere [Reference PodestàPod97]. More generally, the focal submanifolds of isoparametric families of hypersurfaces with constant principal curvatures [Reference Ge and TangGT14] (such as the famous inhomogeneous examples in spheres [Reference Ferus, Karcher and MünznerFKM81]), or of previous constructions in symmetric spaces of non-compact type [Reference Díaz-Ramos and Domínguez-VázquezDD13, Reference Domínguez-VázquezDom15, Reference Díaz-Ramos, Domínguez-Vázquez and Rodríguez-VázquezDDR21], are known to be austere. Indeed, the austerity of the focal submanifolds has played a crucial role in the classification of isoparametric hypersurfaces in spheres [Reference MiyaokaMiy13] and complex hyperbolic spaces [Reference Díaz-Ramos, Domínguez-Vázquez and Sanmartín-LópezDDS17]. Theorem A reveals that this property does not hold in general, even in spaces with a large isometry group. For more information on isoparametric hypersurfaces, see [Reference Berndt, Console and OlmosBCO16, Reference Cecil and RyanCR15, Reference ChiChi20a, Reference ChiChi20b].
Third, Theorem A also holds for reducible spaces and yields the first inhomogeneous examples that are not extrinsic products in any reducible symmetric space. For instance, any product of at least three rank-one symmetric spaces of non-compact type turns out to admit inhomogeneous isoparametric hypersurfaces. Particularly remarkable is the case of the product of three real hyperbolic planes, ![]() ${\mathbb {R}} H^2\times {\mathbb {R}} H^2\times {\mathbb {R}} H^2$, which admits such an inhomogeneous example, despite the fact that the isoparametric hypersurfaces of the irreducible factors are all homogeneous. Together with the complex hyperbolic space
${\mathbb {R}} H^2\times {\mathbb {R}} H^2\times {\mathbb {R}} H^2$, which admits such an inhomogeneous example, despite the fact that the isoparametric hypersurfaces of the irreducible factors are all homogeneous. Together with the complex hyperbolic space ![]() ${\mathbb {C}} H^3$ (see [Reference Díaz-Ramos and Domínguez-VázquezDD13]), this reducible space seems to be the lowest-dimensional symmetric space that is known to admit inhomogeneous isoparametric hypersurfaces.
${\mathbb {C}} H^3$ (see [Reference Díaz-Ramos and Domínguez-VázquezDD13]), this reducible space seems to be the lowest-dimensional symmetric space that is known to admit inhomogeneous isoparametric hypersurfaces.
We now describe the construction of the new examples. Let ![]() $M\cong G/K$ be a symmetric space of non-compact type, where
$M\cong G/K$ be a symmetric space of non-compact type, where ![]() $G$ is the connected component of the identity of the isometry group of
$G$ is the connected component of the identity of the isometry group of ![]() $M$, and
$M$, and ![]() $K$ is the isotropy group at some point
$K$ is the isotropy group at some point ![]() $o\in M$. Let
$o\in M$. Let ![]() ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ be the corresponding Cartan decomposition, and
${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ be the corresponding Cartan decomposition, and ![]() ${\mathfrak {a}}$ a maximal abelian subspace of
${\mathfrak {a}}$ a maximal abelian subspace of ![]() ${\mathfrak {p}}$. Consider the restricted root space decomposition
${\mathfrak {p}}$. Consider the restricted root space decomposition ![]() ${\mathfrak {g}}={\mathfrak {g}}_0\oplus (\bigoplus _{\lambda \in \Delta }{\mathfrak {g}}_\lambda )$ with respect to
${\mathfrak {g}}={\mathfrak {g}}_0\oplus (\bigoplus _{\lambda \in \Delta }{\mathfrak {g}}_\lambda )$ with respect to ![]() ${\mathfrak {a}}$, where
${\mathfrak {a}}$, where ![]() $\Delta \subset {\mathfrak {a}}^*$ is the set of restricted roots. Let
$\Delta \subset {\mathfrak {a}}^*$ is the set of restricted roots. Let ![]() $\Delta ^+$ be a choice of positive roots in
$\Delta ^+$ be a choice of positive roots in ![]() $\Delta$, and define
$\Delta$, and define ![]() ${\mathfrak {n}}=\bigoplus _{\lambda \in \Delta ^+}{\mathfrak {g}}_\lambda$. Consider the connected Lie subgroups
${\mathfrak {n}}=\bigoplus _{\lambda \in \Delta ^+}{\mathfrak {g}}_\lambda$. Consider the connected Lie subgroups ![]() $A$,
$A$, ![]() $N$ and
$N$ and ![]() $AN$ of
$AN$ of ![]() $G$ with Lie algebras
$G$ with Lie algebras ![]() ${\mathfrak {a}}$,
${\mathfrak {a}}$, ![]() ${\mathfrak {n}}$ and
${\mathfrak {n}}$ and ![]() ${\mathfrak {a}}\oplus {\mathfrak {n}}$, respectively. The Iwasawa decomposition theorem for
${\mathfrak {a}}\oplus {\mathfrak {n}}$, respectively. The Iwasawa decomposition theorem for ![]() $G$ implies that
$G$ implies that ![]() $M\cong G/K$ is isometric to the solvable Lie group
$M\cong G/K$ is isometric to the solvable Lie group ![]() $AN$ equipped with a left-invariant metric
$AN$ equipped with a left-invariant metric ![]() $\langle \cdot,\cdot \rangle$. For each
$\langle \cdot,\cdot \rangle$. For each ![]() $\lambda \in \Delta$, we define
$\lambda \in \Delta$, we define ![]() $H_\lambda \in {\mathfrak {a}}$ by
$H_\lambda \in {\mathfrak {a}}$ by ![]() $\langle H,H_\lambda \rangle =\lambda (H)$ for all
$\langle H,H_\lambda \rangle =\lambda (H)$ for all ![]() $H\in {\mathfrak {a}}$, and put
$H\in {\mathfrak {a}}$, and put
 \begin{align*} H_\delta=\frac{1}{2}\sum_{\lambda\in\Delta^+}\dim {\mathfrak{g}}_\lambda H_\lambda. \end{align*}
\begin{align*} H_\delta=\frac{1}{2}\sum_{\lambda\in\Delta^+}\dim {\mathfrak{g}}_\lambda H_\lambda. \end{align*}
Theorem 2 Let ![]() $M$ be a symmetric space of non-compact type and rank
$M$ be a symmetric space of non-compact type and rank ![]() $\geq 3$. Let
$\geq 3$. Let ![]() $S$ be the connected Lie subgroup of
$S$ be the connected Lie subgroup of ![]() $AN$ with Lie algebra
$AN$ with Lie algebra ![]() ${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where
${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where ![]() ${\mathfrak {b}}$ is any subspace of codimension at least two of
${\mathfrak {b}}$ is any subspace of codimension at least two of ![]() ${\mathfrak {a}}$ such that
${\mathfrak {a}}$ such that ![]() $H_\delta \in {\mathfrak {b}}$. Then we have the following.
$H_\delta \in {\mathfrak {b}}$. Then we have the following.
(i) The orbit
 $S\cdot o$ is a minimal submanifold. It is non-austere for a generic choice of
$S\cdot o$ is a minimal submanifold. It is non-austere for a generic choice of  ${\mathfrak {b}}$ as above, or if
${\mathfrak {b}}$ as above, or if  $\dim {\mathfrak {b}}=1$.
$\dim {\mathfrak {b}}=1$.(ii) The distance tubes around
 $S\cdot o$ define an inhomogeneous isoparametric family of hypersurfaces with non-constant principal curvatures on
$S\cdot o$ define an inhomogeneous isoparametric family of hypersurfaces with non-constant principal curvatures on  $M$.
$M$.(iii) If two choices of subspaces
 ${\mathfrak {b}}_1$,
${\mathfrak {b}}_1$,  ${\mathfrak {b}}_2$ of
${\mathfrak {b}}_2$ of  ${\mathfrak {a}}$ as above produce congruent isoparametric families, then
${\mathfrak {a}}$ as above produce congruent isoparametric families, then  ${\mathfrak {b}}_2=\varphi ({\mathfrak {b}}_1)$ for some
${\mathfrak {b}}_2=\varphi ({\mathfrak {b}}_1)$ for some  $\varphi$ in the finite group
$\varphi$ in the finite group  $\operatorname {Aut}(\Delta )$ of linear isometries of
$\operatorname {Aut}(\Delta )$ of linear isometries of  ${\mathfrak {a}}$ that leave the subset
${\mathfrak {a}}$ that leave the subset  $\{H_\lambda \in {\mathfrak {a}}: \lambda \in \Delta \}$ invariant.
$\{H_\lambda \in {\mathfrak {a}}: \lambda \in \Delta \}$ invariant.
The condition ![]() $H_\delta \in {\mathfrak {b}}\subset {\mathfrak {a}}$ ensures that the orbit
$H_\delta \in {\mathfrak {b}}\subset {\mathfrak {a}}$ ensures that the orbit ![]() $S\cdot o$ is not only minimal, but an Einstein solvmanifold whenever
$S\cdot o$ is not only minimal, but an Einstein solvmanifold whenever ![]() $M$ is Einstein (for instance, if
$M$ is Einstein (for instance, if ![]() $M$ is irreducible); see Remark 2.1. Theorem B guarantees that any choice of subspace
$M$ is irreducible); see Remark 2.1. Theorem B guarantees that any choice of subspace ![]() ${\mathfrak {b}}$ of codimension at least two in
${\mathfrak {b}}$ of codimension at least two in ![]() ${\mathfrak {a}}$ containing
${\mathfrak {a}}$ containing ![]() $H_\delta$ gives rise to an inhomogeneous isoparametric family of
$H_\delta$ gives rise to an inhomogeneous isoparametric family of ![]() $M$. The genericity condition in item (i) is only needed for the non-austerity of the focal submanifold
$M$. The genericity condition in item (i) is only needed for the non-austerity of the focal submanifold ![]() ${S\cdot o}$. Here, by a generic choice we mean that
${S\cdot o}$. Here, by a generic choice we mean that ![]() ${\mathfrak {b}}$ can be selected in an open dense subset of the Grassmannian of
${\mathfrak {b}}$ can be selected in an open dense subset of the Grassmannian of ![]() $k$-dimensional subspaces of
$k$-dimensional subspaces of ![]() ${\mathfrak {a}}$ containing
${\mathfrak {a}}$ containing ![]() $H_\delta$, for some
$H_\delta$, for some ![]() $k\in \{1,\ldots,\operatorname {rank} M-2\}$. However, genericity can be substituted by explicit computable conditions in terms of the roots. In any case, it is easy to produce concrete examples of non-austere focal sets, the simplest method being just taking
$k\in \{1,\ldots,\operatorname {rank} M-2\}$. However, genericity can be substituted by explicit computable conditions in terms of the roots. In any case, it is easy to produce concrete examples of non-austere focal sets, the simplest method being just taking ![]() ${\mathfrak {b}}={\mathbb {R}} H_\delta$. This implies the first claim of Theorem A. However, Theorem B provides more examples of isoparametric families than Theorem A, as tubes around
${\mathfrak {b}}={\mathbb {R}} H_\delta$. This implies the first claim of Theorem A. However, Theorem B provides more examples of isoparametric families than Theorem A, as tubes around ![]() $S\cdot o$ are always isoparametric with non-constant principal curvatures, independently on whether
$S\cdot o$ are always isoparametric with non-constant principal curvatures, independently on whether ![]() $S \cdot o$ is austere or not, and
$S \cdot o$ is austere or not, and ![]() $S\cdot o$ is actually austere for certain choices of
$S\cdot o$ is actually austere for certain choices of ![]() ${\mathfrak {b}}$. See the discussion around (4)–(6), as well as Remark 2.3, for further details.
${\mathfrak {b}}$. See the discussion around (4)–(6), as well as Remark 2.3, for further details.
If ![]() $\operatorname {rank} M=\dim {\mathfrak {a}}\geq 4$, then there are uncountably many subspaces
$\operatorname {rank} M=\dim {\mathfrak {a}}\geq 4$, then there are uncountably many subspaces ![]() ${\mathfrak {b}}$ of codimension at least two in
${\mathfrak {b}}$ of codimension at least two in ![]() ${\mathfrak {a}}$ with
${\mathfrak {a}}$ with ![]() $H_\delta \in {\mathfrak {b}}$. By the generic property in Theorem B(i), an uncountable number of such subspaces produce non-austere submanifolds of the form
$H_\delta \in {\mathfrak {b}}$. By the generic property in Theorem B(i), an uncountable number of such subspaces produce non-austere submanifolds of the form ![]() $S\cdot o$. Now, according to Theorem B(iii), tubes around the latter give rise to uncountably many congruence classes of isoparametric families with non-austere focal set. This proves the infiniteness claim in Theorem A. In conclusion, Theorem B clearly implies Theorem A.
$S\cdot o$. Now, according to Theorem B(iii), tubes around the latter give rise to uncountably many congruence classes of isoparametric families with non-austere focal set. This proves the infiniteness claim in Theorem A. In conclusion, Theorem B clearly implies Theorem A.
We would like to point out that Theorem B(iii) and its proof may play an important role in the determination of the congruence classes of homogeneous hyperpolar foliations [Reference Berndt, Díaz-Ramos and TamaruBDT10], which is still an open problem. The relation to hyperpolar foliations stems from the fact that the group ![]() $S$ acts hyperpolarly on
$S$ acts hyperpolarly on ![]() $M$ (see the paragraph below and § 2.4). Our proof of Theorem B(iii) is conceptual and case-free, and does not make use of the assumptions on the rank of
$M$ (see the paragraph below and § 2.4). Our proof of Theorem B(iii) is conceptual and case-free, and does not make use of the assumptions on the rank of ![]() $M$, the codimension of
$M$, the codimension of ![]() ${\mathfrak {b}}$ or
${\mathfrak {b}}$ or ![]() $H_\delta \in {\mathfrak {b}}$. The particular case of
$H_\delta \in {\mathfrak {b}}$. The particular case of ![]() ${\mathfrak {b}}$ of codimension one in
${\mathfrak {b}}$ of codimension one in ![]() ${\mathfrak {a}}$ has been completely characterized in [Reference Berndt and TamaruBT03, pp. 9–20] and [Reference SolonenkoSol21] in terms of the automorphisms of the Dynkin diagram of
${\mathfrak {a}}$ has been completely characterized in [Reference Berndt and TamaruBT03, pp. 9–20] and [Reference SolonenkoSol21] in terms of the automorphisms of the Dynkin diagram of ![]() $M$.
$M$.
We will provide two proofs of the claims of isoparametricity and inhomogeneity in Theorem B(ii). The first is a direct approach based on the study of the extrinsic geometry of the examples via standard Jacobi field theory. The second arises as a straightforward consequence of a new extension method of submanifolds and foliations in symmetric spaces from totally geodesic, flat submanifolds. This method is of independent interest, and seems to have remained unnoticed, despite being an application of the results from [Reference Berndt, Díaz-Ramos and TamaruBDT10] and [Reference Domínguez-VázquezDom15]. Specifically, the action of a group ![]() $S$ as in Theorem B on a symmetric space
$S$ as in Theorem B on a symmetric space ![]() $M$ happens to be free, hyperpolar and with minimal orbits [Reference Berndt, Díaz-Ramos and TamaruBDT10]. Then, a general extension result (for free, polar actions with minimal orbits on Riemannian manifolds) given in [Reference Domínguez-VázquezDom15] by the first author applies, thus allowing submanifolds and singular Riemannian foliations to be extended from a section
$M$ happens to be free, hyperpolar and with minimal orbits [Reference Berndt, Díaz-Ramos and TamaruBDT10]. Then, a general extension result (for free, polar actions with minimal orbits on Riemannian manifolds) given in [Reference Domínguez-VázquezDom15] by the first author applies, thus allowing submanifolds and singular Riemannian foliations to be extended from a section ![]() $\Sigma$ of the polar
$\Sigma$ of the polar ![]() $S$-action to
$S$-action to ![]() $M$. Importantly, this extension procedure preserves various geometric properties such as minimality, polarity or isoparametricity. We refer to [Reference Domínguez-VázquezDom15] (see also [Reference Alexandrino and BettiolAB15] and [Reference Heintze, Liu and OlmosHLO06]) for the definitions of isoparametric submanifold of arbitrary codimension, singular Riemannian foliation, and polar, hyperpolar or isoparametric foliation.
$M$. Importantly, this extension procedure preserves various geometric properties such as minimality, polarity or isoparametricity. We refer to [Reference Domínguez-VázquezDom15] (see also [Reference Alexandrino and BettiolAB15] and [Reference Heintze, Liu and OlmosHLO06]) for the definitions of isoparametric submanifold of arbitrary codimension, singular Riemannian foliation, and polar, hyperpolar or isoparametric foliation.
Theorem 3 Let ![]() $M$ be a symmetric space of non-compact type and rank
$M$ be a symmetric space of non-compact type and rank ![]() ${\geq }3$, and
${\geq }3$, and ![]() $S$ the connected Lie subgroup of
$S$ the connected Lie subgroup of ![]() $AN$ with Lie algebra
$AN$ with Lie algebra ![]() ${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where
${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where ![]() ${\mathfrak {b}}$ is a subspace of codimension at least two of
${\mathfrak {b}}$ is a subspace of codimension at least two of ![]() ${\mathfrak {a}}$ such that
${\mathfrak {a}}$ such that ![]() $H_\delta \in {\mathfrak {b}}$. Let
$H_\delta \in {\mathfrak {b}}$. Let ![]() $\Sigma \cong {\mathbb {R}}^{d}$ be a section of the hyperpolar
$\Sigma \cong {\mathbb {R}}^{d}$ be a section of the hyperpolar ![]() $S$-action on
$S$-action on ![]() $M$, where
$M$, where ![]() $d:=\operatorname {rank} M-\dim {\mathfrak {b}}$.
$d:=\operatorname {rank} M-\dim {\mathfrak {b}}$.
Let ![]() $P$ and
$P$ and ![]() ${\mathcal {F}}$ be a connected submanifold and a singular Riemannian foliation of codimension
${\mathcal {F}}$ be a connected submanifold and a singular Riemannian foliation of codimension ![]() $k$ in the Euclidean space
$k$ in the Euclidean space ![]() $\Sigma \cong {\mathbb {R}}^{d}$, respectively. Then
$\Sigma \cong {\mathbb {R}}^{d}$, respectively. Then
are a connected submanifold and a singular Riemannian foliation of codimension ![]() $k$ in the symmetric space
$k$ in the symmetric space ![]() $M$, respectively. Moreover, we have the following.
$M$, respectively. Moreover, we have the following.
(i) If
 $P$ has parallel mean curvature, is minimal, has flat normal bundle or is isoparametric as a submanifold of
$P$ has parallel mean curvature, is minimal, has flat normal bundle or is isoparametric as a submanifold of  $\Sigma$, the same is true for
$\Sigma$, the same is true for  $S\cdot P$ as a submanifold of
$S\cdot P$ as a submanifold of  $M$. However,
$M$. However,  $S\cdot P$ is never totally geodesic.
$S\cdot P$ is never totally geodesic.(ii) If
 ${\mathcal {F}}$ is a polar (or equivalently, isoparametric) singular Riemannian foliation of
${\mathcal {F}}$ is a polar (or equivalently, isoparametric) singular Riemannian foliation of  $\Sigma$, then
$\Sigma$, then  $S\cdot {\mathcal {F}}$ is an isoparametric and hyperpolar singular Riemannian foliation of
$S\cdot {\mathcal {F}}$ is an isoparametric and hyperpolar singular Riemannian foliation of  $M$.
$M$.(iii) The submanifold
 $S\cdot P$ (respectively, foliation
$S\cdot P$ (respectively, foliation  $S\cdot {\mathcal {F}}$) is inhomogeneous in
$S\cdot {\mathcal {F}}$) is inhomogeneous in  $M$, except if
$M$, except if  $P$ is an affine subspace (respectively, except if
$P$ is an affine subspace (respectively, except if  ${\mathcal {F}}$ is a foliation given by parallel affine subspaces) of
${\mathcal {F}}$ is a foliation given by parallel affine subspaces) of  $\Sigma \cong {\mathbb {R}}^d$.
$\Sigma \cong {\mathbb {R}}^d$.
Under the perspective of the extension procedure described in Theorem C, the isoparametric families of hypersurfaces constructed in Theorem B are nothing but extensions ![]() $S\cdot {\mathcal {F}}$ of the most basic examples of isoparametric foliations
$S\cdot {\mathcal {F}}$ of the most basic examples of isoparametric foliations ![]() ${\mathcal {F}}$ with a singular leaf on a Euclidean space
${\mathcal {F}}$ with a singular leaf on a Euclidean space ![]() ${\mathbb {R}}^d$, namely those given by concentric spheres and their common center. In other words, a tube of radius
${\mathbb {R}}^d$, namely those given by concentric spheres and their common center. In other words, a tube of radius ![]() $t>0$ around
$t>0$ around ![]() $S\cdot o$ (which is a leaf of the isoparametric foliation mentioned in Theorem B(ii)) is the union of
$S\cdot o$ (which is a leaf of the isoparametric foliation mentioned in Theorem B(ii)) is the union of ![]() $S$-orbits passing through the points of a sphere of radius
$S$-orbits passing through the points of a sphere of radius ![]() $t$ in
$t$ in ![]() $\Sigma =\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$ centered at
$\Sigma =\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$ centered at ![]() $o$, where
$o$, where ![]() ${\mathfrak {b}}^\perp$ is the orthogonal complement of
${\mathfrak {b}}^\perp$ is the orthogonal complement of ![]() ${\mathfrak {b}}$ in
${\mathfrak {b}}$ in ![]() ${\mathfrak {a}}$.
${\mathfrak {a}}$.
The general extension result in [Reference Domínguez-VázquezDom15] was applied, in that paper, to a different class of free polar actions with minimal orbits on symmetric spaces of non-compact type. The resulting extension method for symmetric spaces allowed to enlarge submanifolds and foliations from semisimple symmetric spaces of lower rank embedded in a particular totally geodesic manner (namely, as so-called boundary components). This contrasts with the method provided in Theorem C, where one extends submanifolds or foliations from Euclidean spaces. Even more striking is the fact that, whereas the method in [Reference Domínguez-VázquezDom15] preserved the homogeneity of the examples, Theorem C(iii) reveals that this is almost never the case for the extension procedure we present in this article. The ultimate reason for this difference is that the connected component of the identity of the isometry group of a Euclidean space, embedded as a maximal flat in ![]() $M$, does not embed into the isometry group of
$M$, does not embed into the isometry group of ![]() $M$ (only translations do), whereas such an embedding does exist for boundary components of
$M$ (only translations do), whereas such an embedding does exist for boundary components of ![]() $M$.
$M$.
At the topological level, the extension method in Theorem C works as extending submanifolds of a subspace of a Euclidean space by perpendicularly attaching parallel affine subspaces, thus giving rise to a cylinder over the original submanifold. This is so because the ![]() $S$-orbit foliation on
$S$-orbit foliation on ![]() $M$ is diffeomorphically equivalent to a foliation of
$M$ is diffeomorphically equivalent to a foliation of ![]() ${\mathbb {R}}^{\dim M}$ by affine
${\mathbb {R}}^{\dim M}$ by affine ![]() $d$-codimensional subspaces. However, geometrically speaking, the extension procedure in Theorem C is not trivial at all, in that the attached fibers (i.e. the
$d$-codimensional subspaces. However, geometrically speaking, the extension procedure in Theorem C is not trivial at all, in that the attached fibers (i.e. the ![]() $S$-orbits) are minimal, but never totally geodesic.
$S$-orbits) are minimal, but never totally geodesic.
Although it is not the purpose of this paper to exploit the whole potential of Theorem C to produce interesting examples of submanifolds in symmetric spaces of non-compact type, we will briefly illustrate it with some simple applications. For instance, by extending a catenoid in a ![]() $3$-dimensional Euclidean space, we can obtain a complete minimal hypersurface diffeomorphic to
$3$-dimensional Euclidean space, we can obtain a complete minimal hypersurface diffeomorphic to ![]() $\mathbb {S}^1\times {\mathbb {R}}^{\dim M-2}$ on any symmetric space of non-compact type and rank at least
$\mathbb {S}^1\times {\mathbb {R}}^{\dim M-2}$ on any symmetric space of non-compact type and rank at least ![]() $4$. This can, of course, be generalized in several ways, for example by extending (extrinsic products of) minimal surfaces with more complicated topologies. In a different direction, by extending polar foliations on Euclidean spaces, one can obtain (to the best of the authors’ knowledge, the first known examples of) inhomogeneous, isoparametric, hyperpolar, singular Riemannian foliations of codimension higher than one on a non-compact symmetric space
$4$. This can, of course, be generalized in several ways, for example by extending (extrinsic products of) minimal surfaces with more complicated topologies. In a different direction, by extending polar foliations on Euclidean spaces, one can obtain (to the best of the authors’ knowledge, the first known examples of) inhomogeneous, isoparametric, hyperpolar, singular Riemannian foliations of codimension higher than one on a non-compact symmetric space ![]() $M$. Such foliations have no totally geodesic leaves, and can take any codimension
$M$. Such foliations have no totally geodesic leaves, and can take any codimension ![]() $k\in \{1,\ldots, \operatorname {rank} M-2\}$. Moreover, by considering a symmetric space
$k\in \{1,\ldots, \operatorname {rank} M-2\}$. Moreover, by considering a symmetric space ![]() $M$ of sufficiently large rank, one can construct examples with any prescribed polar infinitesimal foliation.
$M$ of sufficiently large rank, one can construct examples with any prescribed polar infinitesimal foliation.
2. Proof of the main theorems
We start by introducing some notation and known facts on symmetric spaces of non-compact type. For more information, we refer the reader to [Reference Díaz-Ramos, Domínguez-Vázquez and Sanmartín-LópezDDS21] and [Reference EberleinEbe96, Chapter 2], and to [Reference KnappKna02, Sections II.5, VI. 4–5] for the theory of root systems.
As in the introduction, let ![]() $M\cong G/K$ be a symmetric space of non-compact type, and
$M\cong G/K$ be a symmetric space of non-compact type, and ![]() ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ the Cartan decomposition determined by the point
${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$ the Cartan decomposition determined by the point ![]() $o\in M$ whose isotropy subgroup of
$o\in M$ whose isotropy subgroup of ![]() $G$ is precisely
$G$ is precisely ![]() $K$. Given a maximal abelian subspace
$K$. Given a maximal abelian subspace ![]() ${\mathfrak {a}}$ of
${\mathfrak {a}}$ of ![]() ${\mathfrak {p}}$, and a covector
${\mathfrak {p}}$, and a covector ![]() $\lambda \in {\mathfrak {a}}^*$, we define
$\lambda \in {\mathfrak {a}}^*$, we define ![]() ${\mathfrak {g}}_\lambda =\{X\in {\mathfrak {g}}:[H,X]=\lambda (H)X \text { for all }H\in {\mathfrak {a}}\}$. The choice of
${\mathfrak {g}}_\lambda =\{X\in {\mathfrak {g}}:[H,X]=\lambda (H)X \text { for all }H\in {\mathfrak {a}}\}$. The choice of ![]() ${\mathfrak {a}}$ determines the set of restricted roots,
${\mathfrak {a}}$ determines the set of restricted roots, ![]() $\Delta =\{\lambda \in {\mathfrak {a}}^*:{\mathfrak {g}}_\lambda \neq 0\}\setminus \{0\}$, and the restricted root space decomposition of
$\Delta =\{\lambda \in {\mathfrak {a}}^*:{\mathfrak {g}}_\lambda \neq 0\}\setminus \{0\}$, and the restricted root space decomposition of ![]() ${\mathfrak {g}}$, namely
${\mathfrak {g}}$, namely ![]() ${\mathfrak {g}}={\mathfrak {g}}_0\oplus (\bigoplus _{\lambda \in \Delta }{\mathfrak {g}}_\lambda )$. The relation
${\mathfrak {g}}={\mathfrak {g}}_0\oplus (\bigoplus _{\lambda \in \Delta }{\mathfrak {g}}_\lambda )$. The relation ![]() $[{\mathfrak {g}}_\lambda,{\mathfrak {g}}_\mu ]\subset {\mathfrak {g}}_{\lambda +\mu }$ holds for any
$[{\mathfrak {g}}_\lambda,{\mathfrak {g}}_\mu ]\subset {\mathfrak {g}}_{\lambda +\mu }$ holds for any ![]() $\lambda$,
$\lambda$, ![]() $\mu \in {\mathfrak {a}}^*$.
$\mu \in {\mathfrak {a}}^*$.
When ![]() ${\mathfrak {a}}^*$ is endowed with the inner product induced by the Killing form of
${\mathfrak {a}}^*$ is endowed with the inner product induced by the Killing form of ![]() ${\mathfrak {g}}$, the subset
${\mathfrak {g}}$, the subset ![]() $\Delta$ of
$\Delta$ of ![]() ${\mathfrak {a}}^*$ turns out to be a (possibly non-reduced) root system. Let
${\mathfrak {a}}^*$ turns out to be a (possibly non-reduced) root system. Let ![]() $\Delta ^+$ be a set of positive roots for
$\Delta ^+$ be a set of positive roots for ![]() $\Delta$, defined as the subset of roots lying at one side of a linear hyperplane in
$\Delta$, defined as the subset of roots lying at one side of a linear hyperplane in ![]() ${\mathfrak {a}}^*$ not intersecting
${\mathfrak {a}}^*$ not intersecting ![]() $\Delta$. Thus,
$\Delta$. Thus, ![]() $\Delta$ is the disjoint union of
$\Delta$ is the disjoint union of ![]() $\Delta ^+$ and
$\Delta ^+$ and ![]() $-\Delta ^+$. We denote by
$-\Delta ^+$. We denote by ![]() $\Pi \subset \Delta ^+$ the corresponding set of simple roots, which is made of all positive roots that are not sums of two positive roots. In particular,
$\Pi \subset \Delta ^+$ the corresponding set of simple roots, which is made of all positive roots that are not sums of two positive roots. In particular, ![]() $\Pi$ is a basis of
$\Pi$ is a basis of ![]() ${\mathfrak {a}}^*$, and every
${\mathfrak {a}}^*$, and every ![]() $\lambda \in \Delta$ is a linear combination of elements in
$\lambda \in \Delta$ is a linear combination of elements in ![]() $\Pi$ whose coefficients are all either non-negative or non-positive integers.
$\Pi$ whose coefficients are all either non-negative or non-positive integers.
We consider the nilpotent Lie algebra ![]() ${\mathfrak {n}}=\bigoplus _{\lambda \in \Delta ^+}{\mathfrak {g}}_\lambda$, and the connected Lie subgroups
${\mathfrak {n}}=\bigoplus _{\lambda \in \Delta ^+}{\mathfrak {g}}_\lambda$, and the connected Lie subgroups ![]() $A$,
$A$, ![]() $N$ and
$N$ and ![]() $AN$ of
$AN$ of ![]() $G$ with Lie algebras
$G$ with Lie algebras ![]() ${\mathfrak {a}}$,
${\mathfrak {a}}$, ![]() ${\mathfrak {n}}$ and
${\mathfrak {n}}$ and ![]() ${\mathfrak {a}}\oplus {\mathfrak {n}}$, respectively. The Iwasawa decomposition theorem for
${\mathfrak {a}}\oplus {\mathfrak {n}}$, respectively. The Iwasawa decomposition theorem for ![]() $G$ implies that
$G$ implies that ![]() $M\cong G/K$ is diffeomorphic to the solvable Lie group
$M\cong G/K$ is diffeomorphic to the solvable Lie group ![]() $AN$. We denote by
$AN$. We denote by ![]() $\langle \cdot, \cdot \rangle$ both the Riemannian metric on
$\langle \cdot, \cdot \rangle$ both the Riemannian metric on ![]() $M$ and the pullback metric on
$M$ and the pullback metric on ![]() $AN$ that makes
$AN$ that makes ![]() $M$ and
$M$ and ![]() $AN$ (as well as
$AN$ (as well as ![]() $T_oM$ and
$T_oM$ and ![]() ${\mathfrak {a}}\oplus {\mathfrak {n}}$) isometric. It turns out that such metric on
${\mathfrak {a}}\oplus {\mathfrak {n}}$) isometric. It turns out that such metric on ![]() $AN$ is left-invariant. Thus, by Koszul's formula, the Levi-Civita connection of
$AN$ is left-invariant. Thus, by Koszul's formula, the Levi-Civita connection of ![]() $AN$ is determined by the expression
$AN$ is determined by the expression ![]() $2\langle \nabla _X Y,Z\rangle =\langle [X,Y],Z\rangle + \langle [Z,X],Y\rangle +\langle X,[Z,Y]\rangle$, for any
$2\langle \nabla _X Y,Z\rangle =\langle [X,Y],Z\rangle + \langle [Z,X],Y\rangle +\langle X,[Z,Y]\rangle$, for any ![]() $X$,
$X$, ![]() $Y$,
$Y$, ![]() $Z\in {\mathfrak {a}}\oplus {\mathfrak {n}}$. In particular, if
$Z\in {\mathfrak {a}}\oplus {\mathfrak {n}}$. In particular, if ![]() $H\in {\mathfrak {a}}$ and
$H\in {\mathfrak {a}}$ and ![]() $X\in {\mathfrak {a}}\oplus {\mathfrak {n}}$, we have
$X\in {\mathfrak {a}}\oplus {\mathfrak {n}}$, we have
For each ![]() $\lambda \in {\mathfrak {a}}^*$, we define the vector
$\lambda \in {\mathfrak {a}}^*$, we define the vector ![]() $H_\lambda \in {\mathfrak {a}}$ by the relation
$H_\lambda \in {\mathfrak {a}}$ by the relation ![]() $\langle H_\lambda,H\rangle =\lambda (H)$ for all
$\langle H_\lambda,H\rangle =\lambda (H)$ for all ![]() $H\in {\mathfrak {a}}$. Particular instances of this definition are the vectors
$H\in {\mathfrak {a}}$. Particular instances of this definition are the vectors ![]() $H_\lambda \in {\mathfrak {a}}$ where
$H_\lambda \in {\mathfrak {a}}$ where ![]() $\lambda \in \Delta \subset {\mathfrak {a}}^*$ is a root, and also the vector
$\lambda \in \Delta \subset {\mathfrak {a}}^*$ is a root, and also the vector ![]() $H_\delta \in {\mathfrak {a}}$, where
$H_\delta \in {\mathfrak {a}}$, where ![]() $\delta =\frac {1}{2}\sum _{\lambda \in \Delta ^+}(\dim {\mathfrak {g}}_\lambda ) \lambda \in {\mathfrak {a}}^*$. We will denote also by
$\delta =\frac {1}{2}\sum _{\lambda \in \Delta ^+}(\dim {\mathfrak {g}}_\lambda ) \lambda \in {\mathfrak {a}}^*$. We will denote also by ![]() $\langle \cdot,\cdot \rangle$ the inner product on
$\langle \cdot,\cdot \rangle$ the inner product on ![]() ${\mathfrak {a}}^*$ given by
${\mathfrak {a}}^*$ given by ![]() $\langle \lambda,\mu \rangle =\langle H_\lambda, H_\mu \rangle$, for any
$\langle \lambda,\mu \rangle =\langle H_\lambda, H_\mu \rangle$, for any ![]() $\lambda,\mu \in {\mathfrak {a}}^*$. With respect to this inner product of
$\lambda,\mu \in {\mathfrak {a}}^*$. With respect to this inner product of ![]() ${\mathfrak {a}}^*$,
${\mathfrak {a}}^*$, ![]() $\Delta$ is also a (possibly non-reduced) root system on
$\Delta$ is also a (possibly non-reduced) root system on ![]() ${\mathfrak {a}}^*$.
${\mathfrak {a}}^*$.
If ![]() $k$ is an isometry of
$k$ is an isometry of ![]() $M$ fixing
$M$ fixing ![]() $o$ and such that
$o$ and such that ![]() $\operatorname {Ad}(k){\mathfrak {a}}={\mathfrak {a}}$, then it is a standard fact that
$\operatorname {Ad}(k){\mathfrak {a}}={\mathfrak {a}}$, then it is a standard fact that ![]() $\operatorname {Ad}(k)$ permutes the root spaces
$\operatorname {Ad}(k)$ permutes the root spaces ![]() ${\mathfrak {g}}_\lambda$ with
${\mathfrak {g}}_\lambda$ with ![]() $\lambda \neq 0$, and given
$\lambda \neq 0$, and given ![]() $\lambda$,
$\lambda$, ![]() $\mu \in \Delta$, the relations
$\mu \in \Delta$, the relations
are equivalent to each other. This follows from the definitions and the fact that ![]() $\operatorname {Ad}(k)$ is an automorphism of
$\operatorname {Ad}(k)$ is an automorphism of ![]() ${\mathfrak {g}}$ and a linear isometry when restricted to
${\mathfrak {g}}$ and a linear isometry when restricted to ![]() ${\mathfrak {a}}$.
${\mathfrak {a}}$.
In the following subsections we will prove Theorems B and C. As already mentioned, Theorem A follows directly from Theorem B.
Let ![]() $S$ be the connected Lie subgroup of
$S$ be the connected Lie subgroup of ![]() $AN$ with Lie algebra
$AN$ with Lie algebra ![]() ${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where
${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$, where ![]() ${\mathfrak {b}}$ is a proper vector subspace of
${\mathfrak {b}}$ is a proper vector subspace of ![]() ${\mathfrak {a}}$. We put
${\mathfrak {a}}$. We put ![]() ${\mathfrak {b}}^\perp :={\mathfrak {a}}\ominus {\mathfrak {b}}$. Hereafter,
${\mathfrak {b}}^\perp :={\mathfrak {a}}\ominus {\mathfrak {b}}$. Hereafter, ![]() $\ominus$ denotes orthogonal complement.
$\ominus$ denotes orthogonal complement.
2.1 Extrinsic geometry and non-austerity of the focal set
In this subsection we will prove Theorem B(i). We first calculate the shape operator ![]() ${\mathcal {S}}$ of
${\mathcal {S}}$ of ![]() $S\cdot o$ as a submanifold of
$S\cdot o$ as a submanifold of ![]() $M$. By homogeneity, it will be enough to calculate
$M$. By homogeneity, it will be enough to calculate ![]() ${\mathcal {S}}$ at
${\mathcal {S}}$ at ![]() $o$. Thanks to the isometry
$o$. Thanks to the isometry ![]() $M\cong AN$ and using (1),
$M\cong AN$ and using (1), ![]() ${\mathcal {S}}$ can be computed as
${\mathcal {S}}$ can be computed as ![]() ${\mathcal {S}}_\xi X=-(\nabla _X \xi )^\top = -[\xi, X]^\top$, where
${\mathcal {S}}_\xi X=-(\nabla _X \xi )^\top = -[\xi, X]^\top$, where ![]() $\xi \in {\mathfrak {b}}^\perp$ and
$\xi \in {\mathfrak {b}}^\perp$ and ![]() $X\in {\mathfrak {s}}$ are left-invariant vector fields on
$X\in {\mathfrak {s}}$ are left-invariant vector fields on ![]() $AN$, and
$AN$, and ![]() $^\top$ denotes orthogonal projection onto the tangent space
$^\top$ denotes orthogonal projection onto the tangent space ![]() ${\mathfrak {s}}$. Using (1), we have
${\mathfrak {s}}$. Using (1), we have
Hence, the mean curvature vector ![]() ${\mathcal {H}}$ of
${\mathcal {H}}$ of ![]() $S\cdot o$ is determined by the relation
$S\cdot o$ is determined by the relation ![]() $\langle {\mathcal {H}},\xi \rangle =\operatorname {tr} {\mathcal {S}}_\xi =\sum _{\lambda \in \Delta ^+} \dim {\mathfrak {g}}_\lambda \lambda (\xi )=2\langle H_\delta,\xi \rangle$, for each
$\langle {\mathcal {H}},\xi \rangle =\operatorname {tr} {\mathcal {S}}_\xi =\sum _{\lambda \in \Delta ^+} \dim {\mathfrak {g}}_\lambda \lambda (\xi )=2\langle H_\delta,\xi \rangle$, for each ![]() $\xi \in {\mathfrak {b}}^\perp$. Thus,
$\xi \in {\mathfrak {b}}^\perp$. Thus, ![]() $S\cdot o$ is minimal if and only if
$S\cdot o$ is minimal if and only if ![]() $H_\delta \in {\mathfrak {s}}$ or, equivalently,
$H_\delta \in {\mathfrak {s}}$ or, equivalently, ![]() $H_\delta \in {\mathfrak {b}}$. This proves the first claim in Theorem B(i).
$H_\delta \in {\mathfrak {b}}$. This proves the first claim in Theorem B(i).
Remark 2.1 The condition ![]() $H_\delta \in {\mathfrak {b}}\subset {\mathfrak {a}}$ also arises in the study of Einstein solvmanifolds. Indeed, this assumption means that
$H_\delta \in {\mathfrak {b}}\subset {\mathfrak {a}}$ also arises in the study of Einstein solvmanifolds. Indeed, this assumption means that ![]() ${\mathfrak {s}}$ contains the mean curvature vector
${\mathfrak {s}}$ contains the mean curvature vector ![]() ${\mathcal {H}}=2H_\delta$ of the solvmanifold
${\mathcal {H}}=2H_\delta$ of the solvmanifold ![]() $AN$ and, thus, if the symmetric metric on
$AN$ and, thus, if the symmetric metric on ![]() $M$ is Einstein (for example, if
$M$ is Einstein (for example, if ![]() $M$ is irreducible), then the orbit
$M$ is irreducible), then the orbit ![]() $S\cdot o$ is known to be Einstein as well, see [Reference HeberHeb98, Theorem 4.18]. Moreover, in this situation, the
$S\cdot o$ is known to be Einstein as well, see [Reference HeberHeb98, Theorem 4.18]. Moreover, in this situation, the ![]() $S$-action on
$S$-action on ![]() $M$ is free and polar with mutually isometric minimal orbits (see § 2.4). The proof of the existence of such an action on any Einstein manifold of negative scalar curvature in the presence of symmetry is one of the key steps in the recent outstanding proof of the Alekseevskii conjecture by Böhm and Lafuente [Reference Böhm and LafuenteBL23].
$M$ is free and polar with mutually isometric minimal orbits (see § 2.4). The proof of the existence of such an action on any Einstein manifold of negative scalar curvature in the presence of symmetry is one of the key steps in the recent outstanding proof of the Alekseevskii conjecture by Böhm and Lafuente [Reference Böhm and LafuenteBL23].
From now on in this subsection and the next (except in Remark 2.2 below), we will assume that ![]() $H_\delta \in {\mathfrak {b}}$ and
$H_\delta \in {\mathfrak {b}}$ and ![]() $\dim {\mathfrak {b}}^\perp \geq 2$ and, hence,
$\dim {\mathfrak {b}}^\perp \geq 2$ and, hence, ![]() $\operatorname {rank} M\geq 3$.
$\operatorname {rank} M\geq 3$.
We will now prove the second claim in Theorem B(i) by showing that ![]() $S\cdot o$ is not austere if
$S\cdot o$ is not austere if ![]() ${\mathfrak {b}}={\mathbb {R}} H_\delta$, and that
${\mathfrak {b}}={\mathbb {R}} H_\delta$, and that ![]() $S\cdot o$ is not austere for a generic choice of a subspace
$S\cdot o$ is not austere for a generic choice of a subspace ![]() ${\mathfrak {b}}$ of
${\mathfrak {b}}$ of ![]() ${\mathfrak {a}}$ containing
${\mathfrak {a}}$ containing ![]() $H_\delta$. From (3) we know that the principal curvatures of
$H_\delta$. From (3) we know that the principal curvatures of ![]() $S\cdot o$, regarded as linear functionals on the normal space
$S\cdot o$, regarded as linear functionals on the normal space ![]() ${\mathfrak {b}}^\perp$, are
${\mathfrak {b}}^\perp$, are ![]() $0$ and the restrictions
$0$ and the restrictions ![]() $\lambda \vert _{{\mathfrak {b}}^\perp }$ of the positive roots
$\lambda \vert _{{\mathfrak {b}}^\perp }$ of the positive roots ![]() $\lambda \in \Delta ^+$. Let
$\lambda \in \Delta ^+$. Let ![]() $\lambda _1,\dots, \lambda _\ell$ be an enumeration of the positive roots in
$\lambda _1,\dots, \lambda _\ell$ be an enumeration of the positive roots in ![]() $\Delta ^+$, where each root
$\Delta ^+$, where each root ![]() $\lambda _i$ is repeated as many times as the dimension
$\lambda _i$ is repeated as many times as the dimension ![]() $\dim {\mathfrak {g}}_{\lambda _i}$ of its associated root space; in particular,
$\dim {\mathfrak {g}}_{\lambda _i}$ of its associated root space; in particular, ![]() $\ell =\dim {\mathfrak {n}}$. Thus,
$\ell =\dim {\mathfrak {n}}$. Thus, ![]() $S\cdot o$ is austere if and only if
$S\cdot o$ is austere if and only if
Note that if ![]() $\lambda$,
$\lambda$, ![]() $\mu \in \Delta ^+$, then
$\mu \in \Delta ^+$, then ![]() $\lambda +\mu$ vanishes on
$\lambda +\mu$ vanishes on ![]() ${\mathfrak {b}}^\perp$ if and only if
${\mathfrak {b}}^\perp$ if and only if ![]() $H_{\lambda +\mu }\in {\mathfrak {b}}$. Therefore, if for some
$H_{\lambda +\mu }\in {\mathfrak {b}}$. Therefore, if for some ![]() $\lambda \in \Delta ^+$ we have
$\lambda \in \Delta ^+$ we have ![]() $H_{\lambda +\mu }\notin {\mathfrak {b}}$ for all
$H_{\lambda +\mu }\notin {\mathfrak {b}}$ for all ![]() $\mu \in \Delta ^+$, then
$\mu \in \Delta ^+$, then ![]() $S\cdot o$ cannot be austere. Assume for a moment that
$S\cdot o$ cannot be austere. Assume for a moment that
Then it follows that ![]() $S\cdot o$ is not austere for the choice
$S\cdot o$ is not austere for the choice ![]() ${\mathfrak {b}}={\mathbb {R}} H_\delta$. More generally, any subspace
${\mathfrak {b}}={\mathbb {R}} H_\delta$. More generally, any subspace ![]() ${\mathfrak {b}}$ of
${\mathfrak {b}}$ of ![]() ${\mathfrak {a}}$ such that
${\mathfrak {a}}$ such that
will produce a non-austere minimal ![]() $S\cdot o$, where
$S\cdot o$, where ![]() $\lambda$ is a fixed root satisfying (5). Observe that the
$\lambda$ is a fixed root satisfying (5). Observe that the ![]() $k$-dimensional subspaces
$k$-dimensional subspaces ![]() ${\mathfrak {b}}$ of
${\mathfrak {b}}$ of ![]() ${\mathfrak {a}}$ satisfying the conditions in (6) constitute an open and dense subset of the space of
${\mathfrak {a}}$ satisfying the conditions in (6) constitute an open and dense subset of the space of ![]() $k$-dimensional subspaces of
$k$-dimensional subspaces of ![]() ${\mathfrak {a}}$ containing
${\mathfrak {a}}$ containing ![]() $H_\delta$, for any
$H_\delta$, for any ![]() $k\in \{1,\dots, \operatorname {rank} M-1\}$. This is because, for any given
$k\in \{1,\dots, \operatorname {rank} M-1\}$. This is because, for any given ![]() $\lambda \in \Delta ^+$ as in (5),
$\lambda \in \Delta ^+$ as in (5), ![]() $\{H_{\lambda +\mu }: \mu \in \Delta ^+\}$ is a finite subset of
$\{H_{\lambda +\mu }: \mu \in \Delta ^+\}$ is a finite subset of ![]() ${\mathfrak {a}}$ not intersecting
${\mathfrak {a}}$ not intersecting ![]() ${\mathbb {R}} H_\delta$.
${\mathbb {R}} H_\delta$.
Thus, in order to conclude the proof of Theorem B(i), we just have to show that (5) is true for any (possibly non-reduced) root system of rank at least ![]() $3$. This is probably well known, but since we did not find an appropriate reference in the literature, we shall give a proof here. We will make frequent use of known properties of root systems, particularly those in [Reference KnappKna02, Proposition 2.48]. We will also use the fact that
$3$. This is probably well known, but since we did not find an appropriate reference in the literature, we shall give a proof here. We will make frequent use of known properties of root systems, particularly those in [Reference KnappKna02, Proposition 2.48]. We will also use the fact that ![]() $\langle \delta, \nu \rangle >0$ for all
$\langle \delta, \nu \rangle >0$ for all ![]() $\nu \in \Delta ^+$. This can be easily shown by adapting the proof of [Reference KnappKna02, Proposition 2.69]. Thus, (5) will be proved if we show that
$\nu \in \Delta ^+$. This can be easily shown by adapting the proof of [Reference KnappKna02, Proposition 2.69]. Thus, (5) will be proved if we show that
We first consider the case that ![]() $\Delta =\Delta _1\oplus \Delta _2$ is a reducible root system. Since
$\Delta =\Delta _1\oplus \Delta _2$ is a reducible root system. Since ![]() $\Delta$ has rank at least
$\Delta$ has rank at least ![]() $3$, we can assume that the (possibly reducible) factor
$3$, we can assume that the (possibly reducible) factor ![]() $\Delta _1$ has rank
$\Delta _1$ has rank ![]() $2$ or higher. Fix
$2$ or higher. Fix ![]() $\lambda \in \Pi \cap \Delta _1$ a simple root in the factor
$\lambda \in \Pi \cap \Delta _1$ a simple root in the factor ![]() $\Delta _1$, and let
$\Delta _1$, and let ![]() $\mu \in \Delta ^+$ be arbitrary. If
$\mu \in \Delta ^+$ be arbitrary. If ![]() $\mu \in \Delta _1$, then any
$\mu \in \Delta _1$, then any ![]() $\nu \in \Delta _2^+$ satisfies
$\nu \in \Delta _2^+$ satisfies ![]() $\langle \lambda +\mu,\nu \rangle =0$. Otherwise, if
$\langle \lambda +\mu,\nu \rangle =0$. Otherwise, if ![]() $\mu \in \Delta _2$, since
$\mu \in \Delta _2$, since ![]() $\operatorname {rank} \Delta _1\geq 2$, there exists
$\operatorname {rank} \Delta _1\geq 2$, there exists ![]() $\nu \in \Pi \cap \Delta _1$,
$\nu \in \Pi \cap \Delta _1$, ![]() $\nu \neq \lambda$, and, hence,
$\nu \neq \lambda$, and, hence, ![]() $\langle \lambda +\mu,\nu \rangle =\langle \lambda,\nu \rangle \leq 0$, since
$\langle \lambda +\mu,\nu \rangle =\langle \lambda,\nu \rangle \leq 0$, since ![]() $\lambda$ and
$\lambda$ and ![]() $\nu$ are simple. This shows (7), and hence (5), in the reducible case.
$\nu$ are simple. This shows (7), and hence (5), in the reducible case.
Now assume that ![]() $\Delta$ is irreducible. Let
$\Delta$ is irreducible. Let ![]() $\lambda \in \Delta ^+$ be such that
$\lambda \in \Delta ^+$ be such that ![]() $|\lambda |\geq |\mu |$ for every
$|\lambda |\geq |\mu |$ for every ![]() $\mu \in \Delta ^+$, and
$\mu \in \Delta ^+$, and ![]() $\lambda \in \Pi$ or
$\lambda \in \Pi$ or ![]() $\lambda /2\in \Pi$ (if
$\lambda /2\in \Pi$ (if ![]() $\Delta$ is non-reduced). Let
$\Delta$ is non-reduced). Let ![]() $\mu \in \Delta ^+$ be arbitrary. If
$\mu \in \Delta ^+$ be arbitrary. If ![]() $\mu \in \Pi$ or if
$\mu \in \Pi$ or if ![]() $\mu /2\in \Pi$ (in case
$\mu /2\in \Pi$ (in case ![]() $\mu$ is non-reduced), then any simple root
$\mu$ is non-reduced), then any simple root ![]() $\nu \in \Pi \setminus \operatorname {span}\{\lambda,\mu \}$ (which exists since
$\nu \in \Pi \setminus \operatorname {span}\{\lambda,\mu \}$ (which exists since ![]() $\operatorname {rank}\Delta \geq 3$) satisfies
$\operatorname {rank}\Delta \geq 3$) satisfies ![]() $\langle \lambda,\nu \rangle \leq 0$ and
$\langle \lambda,\nu \rangle \leq 0$ and ![]() $\langle \mu,\nu \rangle \leq 0$, from where we get (7). Otherwise, assume that
$\langle \mu,\nu \rangle \leq 0$, from where we get (7). Otherwise, assume that ![]() ${\mathbb {R}}\mu \cap \Pi =\emptyset$. Take
${\mathbb {R}}\mu \cap \Pi =\emptyset$. Take ![]() $\nu \in \Pi$ joined to
$\nu \in \Pi$ joined to ![]() $\lambda$ (or to
$\lambda$ (or to ![]() $\lambda /2$ if
$\lambda /2$ if ![]() $\lambda$ is non-reduced) in the Dynkin diagram associated with
$\lambda$ is non-reduced) in the Dynkin diagram associated with ![]() $\Pi$. Then
$\Pi$. Then ![]() $\langle \lambda,\nu \rangle =-|\lambda |^2/2$, and
$\langle \lambda,\nu \rangle =-|\lambda |^2/2$, and ![]() $\langle \mu,\nu \rangle \leq \max \{|\mu |^2,|\nu |^2\}/2\leq |\lambda |^2/2$, where we have used that neither
$\langle \mu,\nu \rangle \leq \max \{|\mu |^2,|\nu |^2\}/2\leq |\lambda |^2/2$, where we have used that neither ![]() $\lambda$ nor
$\lambda$ nor ![]() $\mu$ are proportional to
$\mu$ are proportional to ![]() $\nu$. This implies (7) and, thus, we have concluded the proof of (5), and hence of Theorem B(i).
$\nu$. This implies (7) and, thus, we have concluded the proof of (5), and hence of Theorem B(i).
Remark 2.2 The assumption that ![]() $\operatorname {rank} M\geq 3$ is essential for the proof of the non-austerity claim in Theorem B(i). Specifically, it was crucial in the proof of (7). We did not consider the case
$\operatorname {rank} M\geq 3$ is essential for the proof of the non-austerity claim in Theorem B(i). Specifically, it was crucial in the proof of (7). We did not consider the case ![]() $\operatorname {rank} M = 2$ (with
$\operatorname {rank} M = 2$ (with ![]() $\dim {\mathfrak {b}}=1$) in Theorem B, as it would lead to a minimal leaf
$\dim {\mathfrak {b}}=1$) in Theorem B, as it would lead to a minimal leaf ![]() $S \cdot o$ of a homogeneous (hence, isoparametric) codimension-one regular foliation, and these were classified in [Reference Berndt, Díaz-Ramos and TamaruBDT10]. However, in this case, the austerity of the hypersurface
$S \cdot o$ of a homogeneous (hence, isoparametric) codimension-one regular foliation, and these were classified in [Reference Berndt, Díaz-Ramos and TamaruBDT10]. However, in this case, the austerity of the hypersurface ![]() $S\cdot o$ depends on
$S\cdot o$ depends on ![]() $M$. Indeed, using the characterization in (4), one can check, for instance, that if
$M$. Indeed, using the characterization in (4), one can check, for instance, that if ![]() $M$ is of type
$M$ is of type ![]() $A_2$, then
$A_2$, then ![]() $S\cdot o$ is austere, whereas if
$S\cdot o$ is austere, whereas if ![]() $M$ is of type
$M$ is of type ![]() $B_2$, then it is not.
$B_2$, then it is not.
Remark 2.3 The problem of completely determining the subspaces ![]() ${\mathfrak {b}}$ of
${\mathfrak {b}}$ of ![]() ${\mathfrak {a}}$ that produce austere orbits
${\mathfrak {a}}$ that produce austere orbits ![]() $S\cdot o$ seems to be a non-straightforward combinatorial problem. In this article, we content ourselves with proving that non-austere examples are generic, and with giving some examples (necessarily with
$S\cdot o$ seems to be a non-straightforward combinatorial problem. In this article, we content ourselves with proving that non-austere examples are generic, and with giving some examples (necessarily with ![]() ${\mathbb {R}} H_\delta \subsetneq {\mathfrak {b}}$) which show that austere orbits
${\mathbb {R}} H_\delta \subsetneq {\mathfrak {b}}$) which show that austere orbits ![]() $S\cdot o$ indeed exist.
$S\cdot o$ indeed exist.
Consider ![]() $M=SL_5/SO_5$, let
$M=SL_5/SO_5$, let ![]() $\Delta ^+$ be a set of positive restricted roots (which has
$\Delta ^+$ be a set of positive restricted roots (which has ![]() $10$ elements), and
$10$ elements), and ![]() $\Pi =\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\subset \Delta ^+$ the corresponding set of simple roots (ordered in the standard way, so that
$\Pi =\{\alpha _1,\alpha _2,\alpha _3,\alpha _4\}\subset \Delta ^+$ the corresponding set of simple roots (ordered in the standard way, so that ![]() $\alpha _1$ and
$\alpha _1$ and ![]() $\alpha _4$ correspond to the extremal nodes of the
$\alpha _4$ correspond to the extremal nodes of the ![]() $A_4$-Dynkin diagram). Then
$A_4$-Dynkin diagram). Then ![]() ${\mathfrak {b}}=\operatorname {span}\{H_\lambda, H_{\alpha _2+\alpha _3}\}$ yields an austere orbit
${\mathfrak {b}}=\operatorname {span}\{H_\lambda, H_{\alpha _2+\alpha _3}\}$ yields an austere orbit ![]() $S\cdot o$, where
$S\cdot o$, where ![]() $\lambda =\sum _{i=1}^4\alpha _i$ is the highest root. Indeed, the permutation
$\lambda =\sum _{i=1}^4\alpha _i$ is the highest root. Indeed, the permutation ![]() $\sigma$ of
$\sigma$ of ![]() $\Delta ^+$ given in cycle notation by
$\Delta ^+$ given in cycle notation by ![]() $(\alpha _1\;\lambda -\alpha _1)(\alpha _2\;\alpha _3)(\alpha _4\;\lambda -\alpha _4)(\alpha _1+\alpha _2\;\alpha _3+\alpha _4)$ satisfies the characterization in (4). For an example in the reducible setting, let
$(\alpha _1\;\lambda -\alpha _1)(\alpha _2\;\alpha _3)(\alpha _4\;\lambda -\alpha _4)(\alpha _1+\alpha _2\;\alpha _3+\alpha _4)$ satisfies the characterization in (4). For an example in the reducible setting, let ![]() $M=({\mathbb {R}} H^2)^4$ and denote by
$M=({\mathbb {R}} H^2)^4$ and denote by ![]() $\alpha _1,\alpha _2,\alpha _3,\alpha _4$ the roots in
$\alpha _1,\alpha _2,\alpha _3,\alpha _4$ the roots in ![]() $\Delta ^+=\Pi$. Then, the subspace
$\Delta ^+=\Pi$. Then, the subspace ![]() ${\mathfrak {b}}=\operatorname {span}\{H_{\alpha _1+\alpha _2},H_{\alpha _3+\alpha _4}\}$ of
${\mathfrak {b}}=\operatorname {span}\{H_{\alpha _1+\alpha _2},H_{\alpha _3+\alpha _4}\}$ of ![]() ${\mathfrak {a}}$ produces an austere orbit
${\mathfrak {a}}$ produces an austere orbit ![]() $S\cdot o$, as the permutation
$S\cdot o$, as the permutation ![]() $\sigma$ of
$\sigma$ of ![]() $\Delta ^+$ given by
$\Delta ^+$ given by ![]() $(\alpha _1\; \alpha _2)(\alpha _3\;\alpha _4)$ satisfies (4).
$(\alpha _1\; \alpha _2)(\alpha _3\;\alpha _4)$ satisfies (4).
Remark 2.4 An important subclass of austere submanifolds is that determined by the property that all shape operators for unit normal vectors are isospectral. These were called CPC submanifolds in [Reference Berndt and Sanmartín-LópezBS21]. Their importance stems from the fact that focal sets of isoparametric families of hypersurfaces with constant principal curvatures have this property [Reference Ge and TangGT14], and indeed, in the context of spaces of constant curvature, the classification of CPC submanifolds is equivalent to that of isoparametric hypersurfaces. One may ask if, for some choices ![]() ${\mathfrak {b}}\subset {\mathfrak {a}}$, our construction method produces CPC orbits
${\mathfrak {b}}\subset {\mathfrak {a}}$, our construction method produces CPC orbits ![]() $S\cdot o$. The argument in the last paragraph of § 2.2 will show that this is never the case.
$S\cdot o$. The argument in the last paragraph of § 2.2 will show that this is never the case.
2.2 Tubes around  $S\cdot o$ are isoparametric with non-constant principal curvatures
$S\cdot o$ are isoparametric with non-constant principal curvatures
In this subsection we will prove Theorem B(ii). To this purpose, we will calculate the extrinsic geometry of the distance tubes around ![]() $S\cdot o$ using Jacobi field theory; we refer the reader to [Reference Berndt, Console and OlmosBCO16, § 10.2] for details on this method. Let
$S\cdot o$ using Jacobi field theory; we refer the reader to [Reference Berndt, Console and OlmosBCO16, § 10.2] for details on this method. Let ![]() $\gamma$ be a unit speed geodesic in
$\gamma$ be a unit speed geodesic in ![]() $M$ with
$M$ with ![]() $\gamma (0)=o$ and
$\gamma (0)=o$ and ![]() $\dot {\gamma }(0)=\xi \in \nu _o (S\cdot o)$, where
$\dot {\gamma }(0)=\xi \in \nu _o (S\cdot o)$, where ![]() $\nu (S\cdot o)$ is the normal bundle of
$\nu (S\cdot o)$ is the normal bundle of ![]() $S\cdot o$. Given
$S\cdot o$. Given ![]() $X\in T_o M$, we will denote by
$X\in T_o M$, we will denote by ![]() ${\mathcal {P}}_X$ the parallel vector field along
${\mathcal {P}}_X$ the parallel vector field along ![]() $\gamma$ with
$\gamma$ with ![]() ${\mathcal {P}}_X(0)=X$. For each
${\mathcal {P}}_X(0)=X$. For each ![]() $X\in T_oM\cong {\mathfrak {a}}\oplus {\mathfrak {n}}$ orthogonal to
$X\in T_oM\cong {\mathfrak {a}}\oplus {\mathfrak {n}}$ orthogonal to ![]() $\xi \in \nu _o(S\cdot o)\cong {\mathfrak {b}}^\perp \subset {\mathfrak {a}}$, let
$\xi \in \nu _o(S\cdot o)\cong {\mathfrak {b}}^\perp \subset {\mathfrak {a}}$, let ![]() $J_X$ be the adapted Jacobi vector field along
$J_X$ be the adapted Jacobi vector field along ![]() $\gamma$ that is solution to the initial value problem
$\gamma$ that is solution to the initial value problem
where ![]() $R$ is the curvature tensor of
$R$ is the curvature tensor of ![]() $M$, and
$M$, and ![]() $^\top$,
$^\top$, ![]() $^\perp$ denote the projections onto the tangent and normal spaces of
$^\perp$ denote the projections onto the tangent and normal spaces of ![]() $S\cdot o$, respectively.
$S\cdot o$, respectively.
Let ![]() $H\in {\mathfrak {a}}$ and
$H\in {\mathfrak {a}}$ and ![]() $X_\lambda \in {\mathfrak {g}}_\lambda$,
$X_\lambda \in {\mathfrak {g}}_\lambda$, ![]() $\lambda \in \Delta ^+$, be arbitrary vectors, which we regard as tangent vectors to
$\lambda \in \Delta ^+$, be arbitrary vectors, which we regard as tangent vectors to ![]() $M$ at
$M$ at ![]() $o$. It is well known (see [Reference EberleinEbe96, § 2.15], and note that
$o$. It is well known (see [Reference EberleinEbe96, § 2.15], and note that ![]() $\xi \in {\mathfrak {a}}$) that the parallel vector fields
$\xi \in {\mathfrak {a}}$) that the parallel vector fields ![]() ${\mathcal {P}}_H$ and
${\mathcal {P}}_H$ and ![]() ${\mathcal {P}}_{X_\lambda }$ along the homogeneous geodesic
${\mathcal {P}}_{X_\lambda }$ along the homogeneous geodesic ![]() $\gamma$ are eigenvectors of the Jacobi operator
$\gamma$ are eigenvectors of the Jacobi operator ![]() $R_{\dot {\gamma }}=R(\cdot, \dot {\gamma })\dot {\gamma }$ with respective eigenvalues
$R_{\dot {\gamma }}=R(\cdot, \dot {\gamma })\dot {\gamma }$ with respective eigenvalues ![]() $0$ and
$0$ and ![]() $-\lambda (\xi )^2$. Thus, given arbitrary vectors
$-\lambda (\xi )^2$. Thus, given arbitrary vectors ![]() $\eta \in {\mathfrak {b}}^\perp \ominus {\mathbb {R}}\xi$,
$\eta \in {\mathfrak {b}}^\perp \ominus {\mathbb {R}}\xi$, ![]() $H\in {\mathfrak {b}}\subset {\mathfrak {s}}$ and
$H\in {\mathfrak {b}}\subset {\mathfrak {s}}$ and ![]() $X_\lambda \in {\mathfrak {g}}_\lambda \subset {\mathfrak {s}}$, one can easily verify, taking (3) into account, that the adapted Jacobi fields
$X_\lambda \in {\mathfrak {g}}_\lambda \subset {\mathfrak {s}}$, one can easily verify, taking (3) into account, that the adapted Jacobi fields ![]() $J_\eta$,
$J_\eta$, ![]() $J_H$ and
$J_H$ and ![]() $J_{X_\lambda }$ are given by
$J_{X_\lambda }$ are given by
Since for any ![]() $t>0$ and unit normal vector
$t>0$ and unit normal vector ![]() $\xi \in \nu _o(S\cdot o)$, the set
$\xi \in \nu _o(S\cdot o)$, the set ![]() $\{J_X(t):X\in {T_oM\ominus {\mathbb {R}}\xi }\}$ spans a
$\{J_X(t):X\in {T_oM\ominus {\mathbb {R}}\xi }\}$ spans a ![]() $(\dim M-1)$-dimensional subspace of
$(\dim M-1)$-dimensional subspace of ![]() $T_{\gamma (t)}M$, and taking into account the homogeneity of
$T_{\gamma (t)}M$, and taking into account the homogeneity of ![]() $S\cdot o$, it follows that the tube
$S\cdot o$, it follows that the tube ![]() $W^t:=\{\exp (t\xi ):\xi \in \nu (S\cdot o), |\xi |=1\}$ of radius
$W^t:=\{\exp (t\xi ):\xi \in \nu (S\cdot o), |\xi |=1\}$ of radius ![]() $t$ around
$t$ around ![]() $S\cdot o$ is indeed a hypersurface of
$S\cdot o$ is indeed a hypersurface of ![]() $M$, for any
$M$, for any ![]() $t>0$. Moreover, the shape operator
$t>0$. Moreover, the shape operator ![]() ${\mathcal {S}}^t$ of
${\mathcal {S}}^t$ of ![]() $W^t$ with respect to the normal vector
$W^t$ with respect to the normal vector ![]() $\dot {\gamma }(t)$ can be calculated by
$\dot {\gamma }(t)$ can be calculated by ![]() ${\mathcal {S}}^tJ_X(t)=-J_X'(t)$, for each
${\mathcal {S}}^tJ_X(t)=-J_X'(t)$, for each ![]() $X\in T_oM\ominus {\mathbb {R}}\xi$. Therefore, inserting (8) into the previous relation, we obtain
$X\in T_oM\ominus {\mathbb {R}}\xi$. Therefore, inserting (8) into the previous relation, we obtain
for any ![]() $\eta \in {\mathfrak {b}}^\perp \ominus {\mathbb {R}} \xi$,
$\eta \in {\mathfrak {b}}^\perp \ominus {\mathbb {R}} \xi$, ![]() $H\in {\mathfrak {b}}\subset {\mathfrak {s}}$ and
$H\in {\mathfrak {b}}\subset {\mathfrak {s}}$ and ![]() $X_\lambda \in {\mathfrak {g}}_\lambda \subset {\mathfrak {s}}$. Thus, the mean curvature of
$X_\lambda \in {\mathfrak {g}}_\lambda \subset {\mathfrak {s}}$. Thus, the mean curvature of ![]() $W^t$ is
$W^t$ is
 \[ {\mathcal{H}}^t=\operatorname{tr} {\mathcal{S}}^t=-\frac{1}{t}(\dim {\mathfrak{b}}^\perp-1)+ \sum_{\lambda\in\Delta^+}\dim{\mathfrak{g}}_\lambda\lambda(\xi)=-\frac{1}{t}(\dim {\mathfrak{b}}^\perp-1), \]
\[ {\mathcal{H}}^t=\operatorname{tr} {\mathcal{S}}^t=-\frac{1}{t}(\dim {\mathfrak{b}}^\perp-1)+ \sum_{\lambda\in\Delta^+}\dim{\mathfrak{g}}_\lambda\lambda(\xi)=-\frac{1}{t}(\dim {\mathfrak{b}}^\perp-1), \]
where in the last equality we have used the assumption that ![]() $H_\delta$ is orthogonal to any normal vector
$H_\delta$ is orthogonal to any normal vector ![]() $\xi$. This shows that each tube
$\xi$. This shows that each tube ![]() $W^t$ has constant mean curvature. As discussed in the introduction, each
$W^t$ has constant mean curvature. As discussed in the introduction, each ![]() $W^t$ is the union of the
$W^t$ is the union of the ![]() $S$-orbits passing through the points of a sphere of radius
$S$-orbits passing through the points of a sphere of radius ![]() $t$ centered at
$t$ centered at ![]() $o$ in the Euclidean space
$o$ in the Euclidean space ![]() $\Sigma :=\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$. Since the action of
$\Sigma :=\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$. Since the action of ![]() $S\subset AN$ on
$S\subset AN$ on ![]() $M$ is free and, by construction, the tubes
$M$ is free and, by construction, the tubes ![]() $W^t$ are equidistant to each other and to
$W^t$ are equidistant to each other and to ![]() $S\cdot o$, we conclude that
$S\cdot o$, we conclude that ![]() $\{W^t:t>0\}\cup \{S\cdot o\}$ is a isoparametric family of hypersurfaces with focal set
$\{W^t:t>0\}\cup \{S\cdot o\}$ is a isoparametric family of hypersurfaces with focal set ![]() $S\cdot o$.
$S\cdot o$.
Finally, the non-constancy of the principal curvatures of ![]() $W^t$, and hence the inhomogeneity of
$W^t$, and hence the inhomogeneity of ![]() $W^t$, follows directly from [Reference Ge and TangGT14, Theorem 1.2] when
$W^t$, follows directly from [Reference Ge and TangGT14, Theorem 1.2] when ![]() $S \cdot o$ is not austere. However, we can provide an easy argument, based on (9), which works in general, independently of whether
$S \cdot o$ is not austere. However, we can provide an easy argument, based on (9), which works in general, independently of whether ![]() $S \cdot o$ is austere or not. Indeed, if the principal curvatures of some tube
$S \cdot o$ is austere or not. Indeed, if the principal curvatures of some tube ![]() $W^t$ around
$W^t$ around ![]() $S \cdot o$ were constant, the set
$S \cdot o$ were constant, the set ![]() $\{\lambda (\xi ):\lambda \in \Delta ^+,\xi \in {\mathfrak {b}}^\perp, |\xi |=1\}$ would be finite. Note that such set is also constant if
$\{\lambda (\xi ):\lambda \in \Delta ^+,\xi \in {\mathfrak {b}}^\perp, |\xi |=1\}$ would be finite. Note that such set is also constant if ![]() $S\cdot o$ is assumed to be CPC (cf. Remark 2.4). Since
$S\cdot o$ is assumed to be CPC (cf. Remark 2.4). Since ![]() $\dim {\mathfrak {b}}^\perp \geq 2$, this would necessarily imply
$\dim {\mathfrak {b}}^\perp \geq 2$, this would necessarily imply ![]() ${\mathfrak {b}}^\perp \subset \ker \lambda$ for all
${\mathfrak {b}}^\perp \subset \ker \lambda$ for all ![]() $\lambda \in \Delta ^+$, which is impossible, as
$\lambda \in \Delta ^+$, which is impossible, as ![]() $\Delta ^+$ generates
$\Delta ^+$ generates ![]() ${\mathfrak {a}}^*$. This concludes the proof of item (ii) of Theorem B and of Remark 2.4.
${\mathfrak {a}}^*$. This concludes the proof of item (ii) of Theorem B and of Remark 2.4.
2.3 Congruence of the examples
This subsection contains the proof of Theorem B(iii). More specifically, let ![]() ${\mathfrak {b}}_1$,
${\mathfrak {b}}_1$, ![]() ${\mathfrak {b}}_2$ be two vector subspaces of
${\mathfrak {b}}_2$ be two vector subspaces of ![]() ${\mathfrak {a}}$, and let
${\mathfrak {a}}$, and let ![]() $S_i$ be the connected Lie subgroup of
$S_i$ be the connected Lie subgroup of ![]() $AN$ with Lie algebra
$AN$ with Lie algebra ![]() ${\mathfrak {s}}_i={\mathfrak {b}}_i\oplus {\mathfrak {n}}$,
${\mathfrak {s}}_i={\mathfrak {b}}_i\oplus {\mathfrak {n}}$, ![]() $i\in \{1,2\}$. We will prove that if the orbits
$i\in \{1,2\}$. We will prove that if the orbits ![]() $S_1\cdot o$ and
$S_1\cdot o$ and ![]() $S_2\cdot o$ are congruent, then
$S_2\cdot o$ are congruent, then ![]() ${\mathfrak {b}}_2=\varphi ({\mathfrak {b}}_1)$ for some linear isometry
${\mathfrak {b}}_2=\varphi ({\mathfrak {b}}_1)$ for some linear isometry ![]() $\varphi$ of
$\varphi$ of ![]() ${\mathfrak {a}}$ of the form
${\mathfrak {a}}$ of the form ![]() $\varphi =\operatorname {Ad}(k)\vert _{\mathfrak {a}}$,
$\varphi =\operatorname {Ad}(k)\vert _{\mathfrak {a}}$, ![]() $k\in N_{\widehat {K}}({\mathfrak {a}})$. Here
$k\in N_{\widehat {K}}({\mathfrak {a}})$. Here ![]() $N_{\widehat {K}}({\mathfrak {a}})$ denotes the normalizer of
$N_{\widehat {K}}({\mathfrak {a}})$ denotes the normalizer of ![]() ${\mathfrak {a}}$ in the full isotropy group
${\mathfrak {a}}$ in the full isotropy group ![]() $\widehat {K}=\{k\in \mathrm {Isom}(M):k(o)=o\}$. Note that the group
$\widehat {K}=\{k\in \mathrm {Isom}(M):k(o)=o\}$. Note that the group ![]() $\{\operatorname {Ad}(k)\vert _{\mathfrak {a}}:k\in N_{\widehat {K}}({\mathfrak {a}})\}$ leaves the finite set
$\{\operatorname {Ad}(k)\vert _{\mathfrak {a}}:k\in N_{\widehat {K}}({\mathfrak {a}})\}$ leaves the finite set ![]() $\{H_\lambda \in {\mathfrak {a}}:\lambda \in \Delta \}$ invariant, see (2). It is therefore a finite group, as the
$\{H_\lambda \in {\mathfrak {a}}:\lambda \in \Delta \}$ invariant, see (2). It is therefore a finite group, as the ![]() $H_\lambda$,
$H_\lambda$, ![]() $\lambda \in \Delta$, generate
$\lambda \in \Delta$, generate ![]() ${\mathfrak {a}}$.
${\mathfrak {a}}$.
We will not assume any restriction on the rank of ![]() $M$ or on the subspaces
$M$ or on the subspaces ![]() ${\mathfrak {b}}_1$ and
${\mathfrak {b}}_1$ and ![]() ${\mathfrak {b}}_2$. Observe that Theorem B(iii) will then follow directly, since two choices of subspaces
${\mathfrak {b}}_2$. Observe that Theorem B(iii) will then follow directly, since two choices of subspaces ![]() ${\mathfrak {b}}_1$,
${\mathfrak {b}}_1$, ![]() ${\mathfrak {b}}_2$ of
${\mathfrak {b}}_2$ of ![]() ${\mathfrak {a}}$ in the conditions of Theorem B produce congruent isoparametric families if and only if the orbits
${\mathfrak {a}}$ in the conditions of Theorem B produce congruent isoparametric families if and only if the orbits ![]() $S_1\cdot o$ and
$S_1\cdot o$ and ![]() $S_2\cdot o$ are congruent.
$S_2\cdot o$ are congruent.
Assume that ![]() $S_1\cdot o$ and
$S_1\cdot o$ and ![]() $S_2\cdot o$ are congruent submanifolds of
$S_2\cdot o$ are congruent submanifolds of ![]() $M$. By composing with an element of
$M$. By composing with an element of ![]() $S_2$ if necessary, we can assume that there is an isometry
$S_2$ if necessary, we can assume that there is an isometry ![]() $k\in \widehat {K}$ of
$k\in \widehat {K}$ of ![]() $M$ fixing
$M$ fixing ![]() $o$ and such that
$o$ and such that ![]() $k(S_1\cdot o)=S_2\cdot o$. Then
$k(S_1\cdot o)=S_2\cdot o$. Then ![]() $k_*(\nu _o(S_1\cdot o))=\nu _o(S_2\cdot o)$, which translates into
$k_*(\nu _o(S_1\cdot o))=\nu _o(S_2\cdot o)$, which translates into ![]() $\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$, as
$\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$, as ![]() ${\mathfrak {b}}_i^\perp ={\mathfrak {a}}\ominus {\mathfrak {b}}_i$ is a subspace of
${\mathfrak {b}}_i^\perp ={\mathfrak {a}}\ominus {\mathfrak {b}}_i$ is a subspace of ![]() ${\mathfrak {p}}$, for each
${\mathfrak {p}}$, for each ![]() $i\in \{1,2\}$. Now, Theorem B(iii) follows directly from the following.
$i\in \{1,2\}$. Now, Theorem B(iii) follows directly from the following.
Lemma 2.5 Let ![]() ${\mathfrak {b}}_1$,
${\mathfrak {b}}_1$, ![]() ${\mathfrak {b}}_2$ be subspaces of
${\mathfrak {b}}_2$ be subspaces of ![]() ${\mathfrak {a}}$ such that
${\mathfrak {a}}$ such that ![]() $\operatorname {Ad} (k) {\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$ for some
$\operatorname {Ad} (k) {\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$ for some ![]() $k\in \widehat {K}$. Then, there exists
$k\in \widehat {K}$. Then, there exists ![]() $\tilde {k} \in N_{\widehat {K}}({\mathfrak {a}})$ such that
$\tilde {k} \in N_{\widehat {K}}({\mathfrak {a}})$ such that ![]() $\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$.
$\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$.
Proof. For each ![]() $i\in \{1,2\}$, define
$i\in \{1,2\}$, define ![]() $\Delta _i^+:= \{\lambda \in \Delta ^+:\lambda ({{\mathfrak {b}}_i^\perp })=0\}$ and
$\Delta _i^+:= \{\lambda \in \Delta ^+:\lambda ({{\mathfrak {b}}_i^\perp })=0\}$ and ![]() ${\mathfrak {a}}_i:=\bigcap _{\lambda \in \Delta _i^+}\ker \lambda$. By definition,
${\mathfrak {a}}_i:=\bigcap _{\lambda \in \Delta _i^+}\ker \lambda$. By definition, ![]() ${\mathfrak {b}}_i^\perp \subset {\mathfrak {a}}_i$. It turns out that the centralizer of
${\mathfrak {b}}_i^\perp \subset {\mathfrak {a}}_i$. It turns out that the centralizer of ![]() ${\mathfrak {b}}_i^\perp$ in
${\mathfrak {b}}_i^\perp$ in ![]() ${\mathfrak {p}}$ is a Lie triple system of the form
${\mathfrak {p}}$ is a Lie triple system of the form ![]() $Z_{\mathfrak {p}}({\mathfrak {b}}_i^\perp )={\mathfrak {a}}_i\oplus {\mathfrak {c}}_i$, where
$Z_{\mathfrak {p}}({\mathfrak {b}}_i^\perp )={\mathfrak {a}}_i\oplus {\mathfrak {c}}_i$, where ![]() ${\mathfrak {c}}_i=({\mathfrak {a}}\ominus {\mathfrak {a}}_i)\oplus (\bigoplus _{\lambda \in \Delta _i^+}{\mathfrak {p}}_\lambda )$,
${\mathfrak {c}}_i=({\mathfrak {a}}\ominus {\mathfrak {a}}_i)\oplus (\bigoplus _{\lambda \in \Delta _i^+}{\mathfrak {p}}_\lambda )$, ![]() ${\mathfrak {p}}_\lambda =(1-\theta ){\mathfrak {g}}_\lambda \subset {\mathfrak {p}}$, and
${\mathfrak {p}}_\lambda =(1-\theta ){\mathfrak {g}}_\lambda \subset {\mathfrak {p}}$, and ![]() $\theta$ is the Cartan involution associated with the decomposition
$\theta$ is the Cartan involution associated with the decomposition ![]() ${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$; see [Reference EberleinEbe96, § 2.20] for details. Both
${\mathfrak {g}}={\mathfrak {k}}\oplus {\mathfrak {p}}$; see [Reference EberleinEbe96, § 2.20] for details. Both ![]() ${\mathfrak {a}}_i$ and
${\mathfrak {a}}_i$ and ![]() ${\mathfrak {c}}_i$ are also (mutually orthogonal) Lie triple systems, corresponding to a totally geodesic flat submanifold
${\mathfrak {c}}_i$ are also (mutually orthogonal) Lie triple systems, corresponding to a totally geodesic flat submanifold ![]() $\operatorname {Exp}({\mathfrak {a}}_i)\cdot o\cong {\mathbb {R}}^{r-r_i}$ and a totally geodesic semisimple symmetric space of non-compact type
$\operatorname {Exp}({\mathfrak {a}}_i)\cdot o\cong {\mathbb {R}}^{r-r_i}$ and a totally geodesic semisimple symmetric space of non-compact type ![]() $C_i:=\operatorname {Exp}({\mathfrak {c}}_i)\cdot o$ of rank
$C_i:=\operatorname {Exp}({\mathfrak {c}}_i)\cdot o$ of rank ![]() $r_i$, respectively, where
$r_i$, respectively, where ![]() $r:=\operatorname {rank} M=|\Pi |$ and
$r:=\operatorname {rank} M=|\Pi |$ and ![]() $r_i=\dim ({\mathfrak {a}}\ominus {\mathfrak {a}}_i)$ is the maximum number of linearly independent roots in
$r_i=\dim ({\mathfrak {a}}\ominus {\mathfrak {a}}_i)$ is the maximum number of linearly independent roots in ![]() $\Delta _i^+$. Since
$\Delta _i^+$. Since ![]() $\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$, we also have
$\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$, we also have ![]() $\operatorname {Ad}(k)Z_{\mathfrak {p}}({\mathfrak {b}}_1^\perp )=Z_{\mathfrak {p}}({\mathfrak {b}}_2^\perp )$ and, hence,
$\operatorname {Ad}(k)Z_{\mathfrak {p}}({\mathfrak {b}}_1^\perp )=Z_{\mathfrak {p}}({\mathfrak {b}}_2^\perp )$ and, hence, ![]() $\operatorname {Ad}(k)({\mathfrak {a}}_1\oplus {\mathfrak {c}}_1)={\mathfrak {a}}_2\oplus {\mathfrak {c}}_2$. Thus,
$\operatorname {Ad}(k)({\mathfrak {a}}_1\oplus {\mathfrak {c}}_1)={\mathfrak {a}}_2\oplus {\mathfrak {c}}_2$. Thus, ![]() $k$ maps the totally geodesic submanifold
$k$ maps the totally geodesic submanifold ![]() ${\mathbb {R}}^{r-r_1}\times C_1$ to
${\mathbb {R}}^{r-r_1}\times C_1$ to ![]() ${\mathbb {R}}^{r-r_2}\times C_2$, and then
${\mathbb {R}}^{r-r_2}\times C_2$, and then ![]() $k$ necessarily preserves the Euclidean and semisimple factors, from where
$k$ necessarily preserves the Euclidean and semisimple factors, from where ![]() $\operatorname {Ad}(k){\mathfrak {a}}_1={\mathfrak {a}}_2$ and
$\operatorname {Ad}(k){\mathfrak {a}}_1={\mathfrak {a}}_2$ and ![]() $\operatorname {Ad}(k){\mathfrak {c}}_1={\mathfrak {c}}_2$.
$\operatorname {Ad}(k){\mathfrak {c}}_1={\mathfrak {c}}_2$.
Let ![]() $K_i$ be the connected component of the identity of the isotropy group of
$K_i$ be the connected component of the identity of the isotropy group of ![]() $C_i$ at
$C_i$ at ![]() $o$. Its Lie algebra is
$o$. Its Lie algebra is ![]() ${\mathfrak {k}}_i=[{\mathfrak {c}}_i,{\mathfrak {c}}_i]$. Note that
${\mathfrak {k}}_i=[{\mathfrak {c}}_i,{\mathfrak {c}}_i]$. Note that ![]() ${\mathfrak {a}}\ominus {\mathfrak {a}}_2$ and
${\mathfrak {a}}\ominus {\mathfrak {a}}_2$ and ![]() $\operatorname {Ad}(k)({\mathfrak {a}}\ominus {\mathfrak {a}}_1)\subset \operatorname {Ad}(k){\mathfrak {c}}_1={\mathfrak {c}}_2$ are maximal abelian subspaces of
$\operatorname {Ad}(k)({\mathfrak {a}}\ominus {\mathfrak {a}}_1)\subset \operatorname {Ad}(k){\mathfrak {c}}_1={\mathfrak {c}}_2$ are maximal abelian subspaces of ![]() ${\mathfrak {c}}_2$. Since any two maximal abelian subspaces of the tangent space of a symmetric space are conjugate, there exists
${\mathfrak {c}}_2$. Since any two maximal abelian subspaces of the tangent space of a symmetric space are conjugate, there exists ![]() $k'\in K_2$ such that the element
$k'\in K_2$ such that the element ![]() $\tilde {k}:=k'k\in \widehat {K}$ satisfies
$\tilde {k}:=k'k\in \widehat {K}$ satisfies ![]() $\operatorname {Ad}(\tilde {k})({\mathfrak {a}}\ominus {\mathfrak {a}}_1)={\mathfrak {a}}\ominus {\mathfrak {a}}_2$. As
$\operatorname {Ad}(\tilde {k})({\mathfrak {a}}\ominus {\mathfrak {a}}_1)={\mathfrak {a}}\ominus {\mathfrak {a}}_2$. As ![]() ${\mathfrak {k}}_2=[{\mathfrak {c}}_2,{\mathfrak {c}}_2]$ centralizes
${\mathfrak {k}}_2=[{\mathfrak {c}}_2,{\mathfrak {c}}_2]$ centralizes ![]() ${\mathfrak {a}}_2$, then
${\mathfrak {a}}_2$, then ![]() $\operatorname {Ad}(k')$ leaves
$\operatorname {Ad}(k')$ leaves ![]() ${\mathfrak {a}}_2$ (and, hence,
${\mathfrak {a}}_2$ (and, hence, ![]() ${\mathfrak {b}}_2^\perp$) pointwise invariant. This, together with
${\mathfrak {b}}_2^\perp$) pointwise invariant. This, together with ![]() $\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$,
$\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$, ![]() $\operatorname {Ad}(k){\mathfrak {a}}_1={\mathfrak {a}}_2$ and
$\operatorname {Ad}(k){\mathfrak {a}}_1={\mathfrak {a}}_2$ and ![]() $\operatorname {Ad}(\tilde {k})({\mathfrak {a}}\ominus {\mathfrak {a}}_1)={\mathfrak {a}}\ominus {\mathfrak {a}}_2$, implies
$\operatorname {Ad}(\tilde {k})({\mathfrak {a}}\ominus {\mathfrak {a}}_1)={\mathfrak {a}}\ominus {\mathfrak {a}}_2$, implies ![]() $\operatorname {Ad}(\tilde {k}){\mathfrak {a}}={\mathfrak {a}}$ and
$\operatorname {Ad}(\tilde {k}){\mathfrak {a}}={\mathfrak {a}}$ and ![]() $\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$, as we wanted to show.
$\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$, as we wanted to show.
2.4 Extension method and proof of Theorem C
The Lie group ![]() $AN$ acts simply transitively on
$AN$ acts simply transitively on ![]() $M$. Hence, the connected Lie subgroup
$M$. Hence, the connected Lie subgroup ![]() $S$ of
$S$ of ![]() $AN$ with Lie algebra
$AN$ with Lie algebra ![]() ${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$ acts freely on
${\mathfrak {s}}={\mathfrak {b}}\oplus {\mathfrak {n}}$ acts freely on ![]() $M$. Moreover, the
$M$. Moreover, the ![]() $S$-action on
$S$-action on ![]() $M$ is hyperpolar with section
$M$ is hyperpolar with section ![]() $\Sigma :={\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o}\cong {\mathbb {R}}^d$, where
$\Sigma :={\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o}\cong {\mathbb {R}}^d$, where ![]() $d=\dim {\mathfrak {b}}^\perp =\operatorname {rank} M-\dim {\mathfrak {b}}$. Indeed, such an
$d=\dim {\mathfrak {b}}^\perp =\operatorname {rank} M-\dim {\mathfrak {b}}$. Indeed, such an ![]() $S$-action is one of the examples of hyperpolar actions with no singular orbits classified in [Reference Berndt, Díaz-Ramos and TamaruBDT10]. Furthermore,
$S$-action is one of the examples of hyperpolar actions with no singular orbits classified in [Reference Berndt, Díaz-Ramos and TamaruBDT10]. Furthermore, ![]() $\Sigma$ intersects each
$\Sigma$ intersects each ![]() $S$-orbit exactly once, as follows from the fact that
$S$-orbit exactly once, as follows from the fact that ![]() $AN= \operatorname {Exp}({\mathfrak {b}}^\perp ) S=S\operatorname {Exp}({\mathfrak {b}}^\perp )$ acts simply transitively on
$AN= \operatorname {Exp}({\mathfrak {b}}^\perp ) S=S\operatorname {Exp}({\mathfrak {b}}^\perp )$ acts simply transitively on ![]() $M$. Since
$M$. Since ![]() $H_\delta \in {\mathfrak {b}}$, the orbit
$H_\delta \in {\mathfrak {b}}$, the orbit ![]() $S\cdot o$ is a minimal submanifold of
$S\cdot o$ is a minimal submanifold of ![]() $M$, as shown in § 2.1. By polarity, any
$M$, as shown in § 2.1. By polarity, any ![]() $S$-orbit is of the form
$S$-orbit is of the form ![]() $S\cdot a(o)=a(a^{-1}Sa\cdot o)=a(S\cdot o)$, for some
$S\cdot a(o)=a(a^{-1}Sa\cdot o)=a(S\cdot o)$, for some ![]() $a\in \operatorname {Exp}({\mathfrak {b}}^\perp )$, where we have used that the group
$a\in \operatorname {Exp}({\mathfrak {b}}^\perp )$, where we have used that the group ![]() $A$ normalizes
$A$ normalizes ![]() $S$. Thus, all
$S$. Thus, all ![]() $S$-orbits are mutually congruent and, hence, minimal (cf. [Reference Berndt, Díaz-Ramos and TamaruBDT10]). Therefore, the action of
$S$-orbits are mutually congruent and, hence, minimal (cf. [Reference Berndt, Díaz-Ramos and TamaruBDT10]). Therefore, the action of ![]() $S$ on
$S$ on ![]() $M$ satisfies the hypotheses of [Reference Domínguez-VázquezDom15, Theorem 2.1], from where the first claim in item (i) as well as item (ii) in Theorem C follow immediately (for item (ii), note that polar singular Riemannian foliations on Euclidean spaces are hyperpolar and isoparametric).
$M$ satisfies the hypotheses of [Reference Domínguez-VázquezDom15, Theorem 2.1], from where the first claim in item (i) as well as item (ii) in Theorem C follow immediately (for item (ii), note that polar singular Riemannian foliations on Euclidean spaces are hyperpolar and isoparametric).
As discussed in [Reference Domínguez-VázquezDom15], the shape operator of an extended submanifold ![]() $S\cdot P$ of
$S\cdot P$ of ![]() $M$, where
$M$, where ![]() $P$ is a submanifold of
$P$ is a submanifold of ![]() $\Sigma$, is block diagonal, with one block corresponding to the shape operator of
$\Sigma$, is block diagonal, with one block corresponding to the shape operator of ![]() $P$, and the other block to the shape operator of the orbit
$P$, and the other block to the shape operator of the orbit ![]() $S\cdot o$. Since the latter never vanishes identically, as follows from (3) and the argument in the last paragraph of § 2.2, we have that
$S\cdot o$. Since the latter never vanishes identically, as follows from (3) and the argument in the last paragraph of § 2.2, we have that ![]() $S\cdot P$ is never totally geodesic, which completes the proof of Theorem C(i).
$S\cdot P$ is never totally geodesic, which completes the proof of Theorem C(i).
We will finally prove item (iii) of Theorem C. Let ![]() $P$ be a submanifold of
$P$ be a submanifold of ![]() $\Sigma$, and
$\Sigma$, and ![]() $S\cdot P$ the extended submanifold of
$S\cdot P$ the extended submanifold of ![]() $M$. We will show that
$M$. We will show that ![]() $S\cdot P$ is a homogeneous submanifold of
$S\cdot P$ is a homogeneous submanifold of ![]() $M$ if and only if
$M$ if and only if ![]() $P$ is an affine subspace of
$P$ is an affine subspace of ![]() $\Sigma \cong {\mathbb {R}}^d$; the analogous claim for foliations stated in item (iii) follows immediately. Note that
$\Sigma \cong {\mathbb {R}}^d$; the analogous claim for foliations stated in item (iii) follows immediately. Note that ![]() $P$ is an affine subspace of
$P$ is an affine subspace of ![]() $\Sigma =\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$ if and only if
$\Sigma =\operatorname {Exp}({\mathfrak {b}}^\perp )\cdot o$ if and only if ![]() $P$ is an orbit
$P$ is an orbit ![]() $L\cdot p$,
$L\cdot p$, ![]() $p\in \Sigma$, of the connected Lie subgroup
$p\in \Sigma$, of the connected Lie subgroup ![]() $L$ of
$L$ of ![]() $A$ whose Lie algebra is a vector subspace
$A$ whose Lie algebra is a vector subspace ![]() ${\mathfrak {l}}$ of
${\mathfrak {l}}$ of ![]() ${\mathfrak {b}}^\perp$. In this case,
${\mathfrak {b}}^\perp$. In this case, ![]() $S\cdot P$ is the orbit of the group
$S\cdot P$ is the orbit of the group ![]() $LS$ through
$LS$ through ![]() $p$ and, thus, it is homogeneous.
$p$ and, thus, it is homogeneous.
Conversely, assume that ![]() $S\cdot P$ is homogeneous. By applying an isometry in
$S\cdot P$ is homogeneous. By applying an isometry in ![]() $A$ if necessary, we can assume that
$A$ if necessary, we can assume that ![]() $o\in P$. Thus, in particular, for each
$o\in P$. Thus, in particular, for each ![]() $p\in P=(S\cdot P)\cap \Sigma$ there exists
$p\in P=(S\cdot P)\cap \Sigma$ there exists ![]() $g_p\in \mathrm {Isom}(M)$ such that
$g_p\in \mathrm {Isom}(M)$ such that ![]() $g_p(o)=p$ and
$g_p(o)=p$ and ![]() $g_p(S\cdot P)=S\cdot P$. Moreover, for each such
$g_p(S\cdot P)=S\cdot P$. Moreover, for each such ![]() $p$ there is exactly one
$p$ there is exactly one ![]() $a_p\in \operatorname {Exp}({\mathfrak {b}}^\perp )\subset A$ such that
$a_p\in \operatorname {Exp}({\mathfrak {b}}^\perp )\subset A$ such that ![]() $a_p(p)=o$. Recall that
$a_p(p)=o$. Recall that ![]() $\widehat {K}=\{k\in \mathrm {Isom}(M):k(o)=o\}$. Define
$\widehat {K}=\{k\in \mathrm {Isom}(M):k(o)=o\}$. Define ![]() $k:=a_pg_p\in \widehat {K}$, which satisfies
$k:=a_pg_p\in \widehat {K}$, which satisfies ![]() $k(S\cdot P)=a_p(S\cdot P)= S\cdot a_p(P)$, since
$k(S\cdot P)=a_p(S\cdot P)= S\cdot a_p(P)$, since ![]() $a_p\in A$ normalizes
$a_p\in A$ normalizes ![]() $S$. Consider the normal spaces at
$S$. Consider the normal spaces at ![]() $o$ to the submanifolds
$o$ to the submanifolds ![]() $S\cdot P$ and
$S\cdot P$ and ![]() $S\cdot a_p(P)$. Since such normal spaces are tangent to
$S\cdot a_p(P)$. Since such normal spaces are tangent to ![]() $\Sigma$, we can identify
$\Sigma$, we can identify ![]() $\nu _o(S\cdot P)\cong {\mathfrak {b}}_1^\perp$ and
$\nu _o(S\cdot P)\cong {\mathfrak {b}}_1^\perp$ and ![]() $\nu _o(S\cdot a_p(P))\cong {\mathfrak {b}}_2^\perp$, for subspaces
$\nu _o(S\cdot a_p(P))\cong {\mathfrak {b}}_2^\perp$, for subspaces ![]() ${\mathfrak {b}}_1^\perp$ and
${\mathfrak {b}}_1^\perp$ and ![]() ${\mathfrak {b}}_2^\perp$ of
${\mathfrak {b}}_2^\perp$ of ![]() ${\mathfrak {b}}^\perp \subset {\mathfrak {a}}$. Since
${\mathfrak {b}}^\perp \subset {\mathfrak {a}}$. Since ![]() $k_*(\nu _o(S\cdot P))=\nu _o(S\cdot a_p(P))$, we have
$k_*(\nu _o(S\cdot P))=\nu _o(S\cdot a_p(P))$, we have ![]() $\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$. Thus, from Lemma 2.5 we deduce the existence of an element
$\operatorname {Ad}(k){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$. Thus, from Lemma 2.5 we deduce the existence of an element ![]() $\tilde {k}\in N_{\widehat {K}}({\mathfrak {a}})$ such that
$\tilde {k}\in N_{\widehat {K}}({\mathfrak {a}})$ such that ![]() $\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$, and hence
$\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1={\mathfrak {b}}_2$, and hence ![]() $\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$. Since
$\operatorname {Ad}(\tilde {k}){\mathfrak {b}}_1^\perp ={\mathfrak {b}}_2^\perp$. Since ![]() $\{\operatorname {Ad}(\hat {k})\vert _{\mathfrak {a}}:\hat {k}\in N_{\widehat {K}}({\mathfrak {a}})\}$ is a finite group of linear isometries of
$\{\operatorname {Ad}(\hat {k})\vert _{\mathfrak {a}}:\hat {k}\in N_{\widehat {K}}({\mathfrak {a}})\}$ is a finite group of linear isometries of ![]() ${\mathfrak {a}}$, then there is only a finite number of normal spaces
${\mathfrak {a}}$, then there is only a finite number of normal spaces ![]() $\nu _o(S\cdot a_p(P))$ for
$\nu _o(S\cdot a_p(P))$ for ![]() $p\in P$. But by the connectedness of
$p\in P$. But by the connectedness of ![]() $P$ and the continuous dependence of
$P$ and the continuous dependence of ![]() $a_p$ on
$a_p$ on ![]() $p$, we must have
$p$, we must have ![]() $\nu _o(S\cdot a_p(P))=\nu _o(S\cdot P)$, for all
$\nu _o(S\cdot a_p(P))=\nu _o(S\cdot P)$, for all ![]() $p\in P$. Equivalently, regarding
$p\in P$. Equivalently, regarding ![]() $P$ and
$P$ and ![]() $a_p(P)$ as submanifolds of
$a_p(P)$ as submanifolds of ![]() $\Sigma \cong {\mathbb {R}}^d$, we have
$\Sigma \cong {\mathbb {R}}^d$, we have ![]() $\nu _o(a_p(P))=\nu _o(P)$, for all
$\nu _o(a_p(P))=\nu _o(P)$, for all ![]() $p\in P$. But the only submanifolds of a Euclidean space
$p\in P$. But the only submanifolds of a Euclidean space ![]() ${\mathbb {R}}^d$ with this property (where the isometries
${\mathbb {R}}^d$ with this property (where the isometries ![]() $a_p$ are translations of
$a_p$ are translations of ![]() ${\mathbb {R}}^d$) are open parts of affine subspaces. The homogeneity of
${\mathbb {R}}^d$) are open parts of affine subspaces. The homogeneity of ![]() $S\cdot P$ implies that
$S\cdot P$ implies that ![]() $P$ must indeed be a complete affine subspace. This concludes the proof of Theorem C.
$P$ must indeed be a complete affine subspace. This concludes the proof of Theorem C.
Acknowledgements
We would like to thank J. Berndt, E. García-Río, J. M. Manzano, H. Tamaru, and the anonymous referees for helpful comments and suggestions. We are grateful to I. Solonenko for pointing out an issue in the study of the congruence in a previous version of this article.
Conflicts of Interest
None.