Let ${\mathcal {D}}$ and $T$ be, respectively, a $C^1$ distribution of $k$-planes and a normal $k$-current on ${\mathbb {R}}^n$. Then ${\mathcal {D}}$ has to be involutive at almost every superdensity point of the tangency set of $T$ with respect to ${\mathcal {D}}$.

Since the celebrated work by Cartan, distributions with small growth vector $(2,3,5)$ have been studied extensively. In the holomorphic setting, there is a natural correspondence between holomorphic $(2,3,5)$-distributions and nondegenerate lines on holomorphic contact manifolds of dimension 5. We generalize this correspondence to higher dimensions by studying nondegenerate lines on holomorphic contact manifolds and the corresponding class of distributions of small growth vector $(2m, 3m, 3m+2)$ for any positive integer m.

In this paper, we develop the theory of singular Hermitian metrics on vector bundles. As an application, we give a structure theorem of a projective manifold X with pseudo-effective tangent bundle; X admits a smooth fibration $X \to Y$ to a flat projective manifold Y such that its general fibre is rationally connected. Moreover, by applying this structure theorem, we classify all the minimal surfaces with pseudo-effective tangent bundle and study general nonminimal surfaces, which provide examples of (possibly singular) positively curved tangent bundles.

As was shown by a part of the authors, for a given 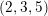$(2,3,5)$-distribution 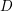$D$ on a five-dimensional manifold $Y$, there is, locally, a Lagrangian cone structure 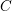$C$ on another five-dimensional manifold 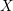$X$ which consists of abnormal or singular paths of $(Y,D)$. We give a characterization of the class of Lagrangian cone structures corresponding to 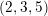$(2,3,5)$-distributions. Thus, we complete the duality between 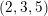$(2,3,5)$-distributions and Lagrangian cone structures via pseudo-product structures of type 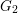$G_{2}$. A local example of nonflat perturbations of the global model of flat Lagrangian cone structure which corresponds to 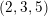$(2,3,5)$-distributions is given.

This paper contributes to the study of Engel structures and their classification. The main result introduces the notion of a loose family of Engel structures and shows that two such families are Engel homotopic if and only if they are formally homotopic. This implies a complete $h$-principle when auxiliary data is fixed. As a corollary, we show that Lorentz and orientable Cartan prolongations are classified up to homotopy by their formal data.

Let $\mathcal{F}$ be a family of vector fields on a manifold or a subcartesian space spanning a distribution $D.$ We prove that an orbit $O$ of $\mathcal{F}$ is an integral manifold of $D$ if $D$ is involutive on $O$ and it has constant rank on $O$. This result implies Frobenius’ theorem, and its various generalizations, on manifolds as well as on subcartesian spaces.

We discuss the Monge problem for under-determined systems of ordinary differential equations with an arbitrary degree of freedom and give a sufficient condition, in terms of truncated multi-flag systems, for the Monge property to hold. This condition extends in a natural way the Cartan criterion valid for systems with one degree of freedom.