Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T09:18:48.032Z Has data issue: false hasContentIssue false
  • English
  • Français

DUALITY OF (2, 3, 5)-DISTRIBUTIONS AND LAGRANGIAN CONE STRUCTURES

Part of: General theory of differentiable manifolds Classical differential geometry Global differential geometry

Published online by Cambridge University Press:  23 January 2020

GOO ISHIKAWA Open the ORCID record for GOO ISHIKAWA [Opens in a new window] ,
YUMIKO KITAGAWA Open the ORCID record for YUMIKO KITAGAWA [Opens in a new window] ,
ASAHI TSUCHIDA Open the ORCID record for ASAHI TSUCHIDA [Opens in a new window]  and
WATARU YUKUNO Open the ORCID record for WATARU YUKUNO [Opens in a new window]
GOO ISHIKAWA
Affiliation:
Hokkaido University, Sapporo060-0810, Japan email ishikawa@math.sci.hokudai.ac.jp
YUMIKO KITAGAWA
Affiliation:
Oita National College of Technology, Oita870-0152, Japan email kitagawa@oita-ct.ac.jp
ASAHI TSUCHIDA
Affiliation:
Institute of Mathematics, Polish Academy of Science, Warszawa00-656, Poland email atsuchida@impan.pl
WATARU YUKUNO
Affiliation:
Hokkaido University, Sapporo060-0810, Japan email yukuwata@math.sci.hokudai.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

As was shown by a part of the authors, for a given 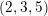$(2,3,5)$-distribution 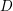$D$ on a five-dimensional manifold 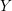$Y$, there is, locally, a Lagrangian cone structure 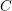$C$ on another five-dimensional manifold 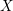$X$ which consists of abnormal or singular paths of 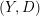$(Y,D)$. We give a characterization of the class of Lagrangian cone structures corresponding to 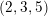$(2,3,5)$-distributions. Thus, we complete the duality between 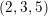$(2,3,5)$-distributions and Lagrangian cone structures via pseudo-product structures of type 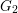$G_{2}$. A local example of nonflat perturbations of the global model of flat Lagrangian cone structure which corresponds to 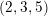$(2,3,5)$-distributions is given.

MSC classification

Primary: 58A30: Vector distributions (subbundles of the tangent bundles)
Secondary: 53A55: Differential invariants (local theory), geometric objects 53C17: Sub-Riemannian geometry 53A20: Projective differential geometry 70F25: Nonholonomic systems
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 303 - 315
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by JSPS KAKENHI No. 15H03615 and No. 15K13431.

References

Agrachev, A. A., Rolling balls and octonions, Proc. Steklov Math. Inst. 258 (2007), 13–22.CrossRefGoogle Scholar
Agrachev, A. A. and Sachkov, Y. L., “Control theory from the geometric viewpoint”, in Control Theory and Optimization, II, Encyclopaedia of Mathematical Sciences 87, Springer, Berlin, 2004.Google Scholar
Agrachev, A. A. and Zelenko, I., Geometry of Jacobi curves, I, J. Dyn. Control Syst. 8(1) (2002), 93–140.CrossRefGoogle Scholar
Agrachev, A. A. and Zelenko, I., Geometry of Jacobi curves, II, J. Dyn. Control Syst. 8(2) (2002), 167–215.CrossRefGoogle Scholar
Agrachev, A. A. and Zelenko, I., “Nurowski’s conformal structures for (2, 5)-distributions via dynamics of abnormal extremals”, in Proceedings of RIMS Symposium on Developments of Cartan Geometry and Related Mathematical Problems, RIMS Kokyuroku 1502, 2006, 204–218.Google Scholar
An, D. and Nurowski, P., Twistor space for rolling bodies, Comm. Math. Phys. 326(2) (2014), 393–414.10.1007/s00220-013-1839-2CrossRefGoogle Scholar
Baez, J. C. and Huerta, J., G 2 and the rolling ball, Trans. Amer. Math. Soc. 366(10) (2014), 5257–5293.CrossRefGoogle Scholar
Bor, G. and Montgomery, R., G 2 and the rolling distributions, Enseign. Math. 55 (2009), 157–196.CrossRefGoogle Scholar
Bryant, R. L., Élie Cartan and geometric duality, A lecture given at the Institut d’Élie Cartan on 19 June 1998.Google Scholar
Bryant, R. L. and Hsu, L., Rigidity of integral curves of rank 2 distributions, Invent. Math. 114(1) (1993), 435–461.CrossRefGoogle Scholar
Bryant, R. L., Chern, S. S., Gardner, R. B., Goldschmidt, H. L. and Griffiths, P. A., Exterior Differential Systems, Springer, New York, 1991.CrossRefGoogle Scholar
C̆ap, A. and Slovák, J., Parabolic Geometries I: Background and General Theory, Mathematical Surveys and Monographs, American Mathematical Society, Providence, RI, 2009.10.1090/surv/154CrossRefGoogle Scholar
Cartan, E., Les systèmes de Pfaff à cinq variables et les équations aux dérivées partielles du second ordre, Ann. Sci. Éc. Norm. Supér. (3) 27 (1910), 109–192.CrossRefGoogle Scholar
Doubrov, B. and Zelenko, I., Equivalence of variational problems of higher order, Differential Geom. Appl. 29 (2011), 255–270.CrossRefGoogle Scholar
Ishikawa, G., Kitagawa, Y. and Yukuno, W., Duality of singular paths for (2, 3, 5)-distributions, J. Dyn. Control Syst. 21 (2015), 155–171.10.1007/s10883-014-9216-9CrossRefGoogle Scholar
Ishikawa, G., Machida, Y. and Takahashi, M., Singularities of tangent surfaces in Cartan’s split G 2 -geometry, Asian J. Math. 20(2) (2016), 353–382.CrossRefGoogle Scholar
Kitagawa, Y., The Infinitesimal automorphisms of a homogeneous subriemannian contact manifold, Thesis, Nara Women’s University, 2005.Google Scholar
Kitagawa, Y., The duality of abnormal extremals on subriemannian Cartan structures, RIMS Kôkyûroku Bessatsu B55 (2016), 111–132.Google Scholar
Leistner, T., Nurowski, P. and Sagerschung, K., New relations between G 2 -geometries in 5 and 7, Int. J. Maths 28(13) (2017), 1750094.Google Scholar
Montgomery, R., A Tour of Subriemannian Geometries, Their Geodesics and Applications, Mathematical Surveys and Monographs 91, American Mathematical Society, Providence, RI, 2002.Google Scholar
Nurowski, P., Differential equations and conformal structures, J. Geom. Phys. 55(1) (2005), 19–49.CrossRefGoogle Scholar
Randall, M., Flat (2, 3, 5)-distributions and Chazy’s equations, Symmetry, Integrability and Geometry: Methods and Applications 12 (2016), 029, 28 pages.Google Scholar
Sato, H., private communication, January 2018.Google Scholar
Tanaka, N., On the equivalence problems associated with simple graded Lie algebras, Hokkaido Math. J. 8 (1979), 23–84.10.14492/hokmj/1381758416CrossRefGoogle Scholar
Tanaka, N., On affine symmetric spaces and the automorphism groups of product manifolds, Hokkaido Math. J. 14 (1985), 277–351.10.14492/hokmj/1381757644CrossRefGoogle Scholar
The, D., Exceptionally simple PDE, Differential Geom. Appl. 56 (2018), 13–41.10.1016/j.difgeo.2017.10.005CrossRefGoogle Scholar
Yamaguchi, K., Differential systems associated with simple graded Lie algebras, Adv. Stud. Pure Math. 22 (1993), 413–494.10.2969/aspm/02210413CrossRefGoogle Scholar
Yamaguchi, K., “G 2 -geometry of overdetermined systems of second order”, in Analysis and Geometry in Several Complex Variables, Birkhäuser, Boston, 1999, 289–314.CrossRefGoogle Scholar
Zelenko, I., Fundamental form and the Cartan tensor of (2, 5)-distributions coincide, J. Dyn. Control Syst. 12(2) (2006), 247–276.10.1007/s10450-006-0383-1CrossRefGoogle Scholar
Zhitomirskii, M., Exact normal form for (2, 5) distributions, RIMS Kokyuroku 1502 (2006), 16–28.Google Scholar