Article contents
LINES ON HOLOMORPHIC CONTACT MANIFOLDS AND A GENERALIZATION OF 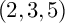 $(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
$(2,3,5)$-DISTRIBUTIONS TO HIGHER DIMENSIONS
Published online by Cambridge University Press: 23 February 2023
Abstract
Since the celebrated work by Cartan, distributions with small growth vector 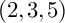 $(2,3,5)$ have been studied extensively. In the holomorphic setting, there is a natural correspondence between holomorphic
$(2,3,5)$ have been studied extensively. In the holomorphic setting, there is a natural correspondence between holomorphic 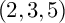 $(2,3,5)$-distributions and nondegenerate lines on holomorphic contact manifolds of dimension 5. We generalize this correspondence to higher dimensions by studying nondegenerate lines on holomorphic contact manifolds and the corresponding class of distributions of small growth vector
$(2,3,5)$-distributions and nondegenerate lines on holomorphic contact manifolds of dimension 5. We generalize this correspondence to higher dimensions by studying nondegenerate lines on holomorphic contact manifolds and the corresponding class of distributions of small growth vector 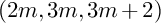 $(2m, 3m, 3m+2)$ for any positive integer m.
$(2m, 3m, 3m+2)$ for any positive integer m.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal
Footnotes
Hwang was supported by the Institute for Basic Science (IBS-R032-D1). Li was supported by the National Natural Science Foundation of China (Grant No. 12201348).
References
- 1
- Cited by


