We study the autophoretic motion of a spherical active particle interacting chemically and hydrodynamically with its fluctuating environment in the limit of rapid diffusion and slow viscous flow. Then, the chemical and hydrodynamic fields can be expressed in terms of integrals. The resulting boundary-domain integral equations provide a direct way of obtaining the traction on the particle, requiring the solution of linear integral equations. An exact solution for the chemical and hydrodynamic problems is obtained for a particle in an unbounded domain. For motion near boundaries, we provide corrections to the unbounded solutions in terms of chemical and hydrodynamic Green's functions, preserving the dissipative nature of autophoresis in a viscous fluid for all physical configurations. Using this, we give the fully stochastic update equations for the Brownian trajectory of an autophoretic particle in a complex environment. First, we analyse the Brownian dynamics of particles capable of complex motion in the bulk. We then introduce a chemically permeable planar surface of two immiscible liquids in the vicinity of the particle and provide explicit solutions to the chemo-hydrodynamics of this system. Finally, we study the case of an isotropically phoretic particle hovering above an interface as a function of interfacial solute permeability and viscosity contrast.

Understanding the effect of intricate surface wettability conditions on microswimmers is crucial for precisely navigating them across narrow microcirculatory networks. Here, we adopt the spherical squirmer model and Navier slip condition to delineate the microswimmer locomotion under a Poiseuille flow in a slit microchannel. Through a combined analytical–numerical approach utilizing bispherical coordinates and the superposition technique, we resolve the slip-modulated simultaneous hydrodynamic interaction with substrate boundaries. Phase portraits reveal that slip significantly alters propulsion mechanisms, destabilizing centreline stable oscillations of pullers beyond a threshold slip length. Superhydrophobic surfaces suppress near-wall rheotaxis states but preserve centreline focusing, facilitating slip-assisted directed transport without surface accumulation. Under strong background flows, subcritical Hopf bifurcation emerges for pullers at a critical slip length, transitioning dynamics from coexisting stable and unstable states to purely unstable behaviour. Contrastingly, for pushers, slip causes a transition from unstable to either stable or fixed-amplitude oscillations. Increased slip length reduces hydrodynamic repulsion on pullers from the walls by enhancing rotational velocity near the walls, whereas it counteracts the torque that causes unstable oscillations of pushers. Three-dimensional analysis of the trajectories reveals the significant role of the out-of-plane orientation of the microswimmer in its transitions between different swimming states. The presented regime maps offer parametric combinations for specific motion behaviours, guiding the development of smart microfluidic drug delivery systems and preventing biofilm deposition in biomedical devices.

Three-dimensional non-rotating odd viscous liquids give rise to Taylor columns and support axisymmetric inertial-like waves (J. Fluid Mech., vol. 973, 2023, A30). When an odd viscous liquid is subjected to rigid-body rotation however, there arise in addition a plethora of other phenomena that need to be clarified. In this paper, we show that three-dimensional incompressible or two-dimensional compressible odd viscous liquids, rotating rigidly with angular velocity $\varOmega$, give rise to both oscillatory and evanescent inertial-like waves or a combination thereof (which we call of mixed type) that can be non-axisymmetric. By evanescent, we mean that along the radial direction, typically when moving away from a solid boundary, the velocity field decreases exponentially. These waves precess in a prograde or retrograde manner with respect to the rotating frame. The oscillatory and evanescent waves resemble respectively the body and wall-modes observed in (non-odd) rotating Rayleigh–Bénard convection (J. Fluid Mech., vol. 248, 1993, pp. 583–604). We show that the three types of waves (wall, body or mixed) can be classified with respect to pairs of planar wavenumbers $\kappa$ which are complex, real or a combination, respectively. Experimentally, by observing the precession rate of the patterns, it would be possible to determine the largely unknown values of the odd viscosity coefficients. This formulation recovers as special cases recent studies of equatorial or topological waves in two-dimensional odd viscous liquids which provided examples of the bulk–interface correspondence at frequencies $\omega <2\varOmega$. We finally point out that the two- and three-dimensional problems are formally equivalent. Their difference then lies in the way data propagate along characteristic rays in three dimensions, which we demonstrate by classifying the resulting Poincaré–Cartan equations.

Communities of swimming microorganisms often thrive near liquid–air interfaces. We study how such ‘active carpets’ shape their aquatic environment by driving biogenic transport in the water column beneath them. The hydrodynamic stirring that active carpets generate leads to diffusive upward fluxes of nutrients from deeper water layers, and downward fluxes of oxygen and carbon. Combining analytical theory and simulations, we examine the biogenic transport by studying fundamental metrics, including the single and pair diffusivity, the first passage time for particle pair encounters and the rate of particle aggregation. Our findings reveal that the hydrodynamic fluctuations driven by active carpets have a region of influence that reaches orders of magnitude further in distance than the size of the organisms. These non-equilibrium fluctuations lead to a strongly enhanced diffusion of particles, which is anisotropic and space dependent. Fluctuations also facilitate encounters of particle pairs, which we quantify by analysing their velocity pair correlation functions as a function of distance between the particles. We found that the size of the particles plays a crucial role in their encounter rates, with larger particles situated near the active carpet being more favourable for aggregation. Overall, this research broadens our comprehension of aquatic systems out of equilibrium and how biologically driven fluctuations contribute to the transport of fundamental elements in biogeochemical cycles.

Understanding the propulsion of a swimmer in a large group of individuals holds the key to unravelling the intriguing dynamics of active matter collective motion. Here, we develop a two-dimensional (2-D) self-assembled rotor, powered by bacterial flagella. At a water–air interface, the average direction of rotation of a rotor is fixed. When the chiral rotor is put into a 2-D bacterial suspension, we examine the average and fluctuation of the angular velocity of the rotor. Remarkably, the average angular velocity of a rotor is found to increase up to 3 times when the density of surrounding bacterial suspension increases and the increase is nonlinear. In a dense suspension of bacteria, the existence of a rotor disrupts vortices in the surrounding active turbulence, and the acceleration of the rotor is independent of the activity level of the surrounding free bacteria. The nonlinear acceleration thus results from hydrodynamic interaction with surrounding crowdedness that can be quantitatively explained by hydrodynamic simulation. The simultaneity between the acceleration of rotor and free bacteria in active turbulence suggests that crowding-induced acceleration may promote the onset of instability. The result will inspire new active-matter-based microfluidic devices with improved transport properties.

The mobility of externally driven phoretic propulsion of particles is evaluated by simultaneously solving the solute conservation equation, interaction potential equation and the modified Stokes equation. While accurate, this approach is cumbersome, especially when the interaction potential decays slowly compared with the particle size. In contrast to external phoresis, the motion of self-phoretic particles is typically estimated by relating the translation and rotation velocities with the local slip velocity. While this approach is convenient and thus widely used, it is only valid when the interaction decay length is significantly smaller than the particle size. Here, by taking inspiration from Brady (J. Fluid Mech., vol. 922, 2021, A10), which combines the benefits of two approaches, we reproduce their unified mobility expressions with arbitrary interaction potentials and show that these expressions can conveniently recover the well-known mobility relationships of external electrophoresis and diffusiophoresis for arbitrary double-layer thickness. Additionally, we show that for a spherical microswimmer, the derived expressions relax to the slip velocity calculations in the limit of the thin interaction length scales. We also employ the derived mobility expressions to calculate the velocities of an autophoretic Janus particle. We find that there is significant dampening in the translation velocity even when the interaction length is an order of magnitude larger than the particle size. Finally, we study the motion of a catalytically self-propelled particle, while it also propels due to external concentration gradients, and demonstrate how the two propulsion modes compete with each other.

Chiral fluids – such as fluids under rotation or a magnetic field as well as synthetic and biological active fluids – flow in a different way than ordinary ones. Due to symmetries broken at the microscopic level, chiral fluids may have asymmetric stress and viscosity tensors, for example giving rise to a hydrostatic torque or non-dissipative (odd) and parity-violating viscosities. In this article, we investigate the motion of rigid bodies in such an anisotropic fluid in the incompressible Stokes regime through the mobility matrix, which encodes the response of a solid body to forces and torques. We demonstrate how the form of the mobility matrix, which is usually determined by particle geometry, can be analogously controlled by the symmetries of the fluid. By computing the mobility matrix for simple shapes in a three-dimensional (3-D) anisotropic chiral fluid, we predict counterintuitive phenomena such as motion at an angle to the direction of applied forces and spinning under the force of gravity.

Microbes play a primary role in wide-ranging biogeochemical and physiological processes, where ambient fluid flows are responsible for cell dispersal as well as mixing of dissolved resources, signalling molecules and biochemical products. Determining the simultaneous (and often coupled) transport properties of actively swimming cells together with passive scalars is key to understanding and ultimately predicting these complex processes. In recent work, Ran & Arratia (J. Fluid Mech., vol. 988, 2024, A25) present the striking observation that dilute concentrations of swimming bacteria severely hinder scalar transport through Lagrangian vortex boundaries in a chaotic flow. Analysis of rotation-dominated regions suggests that local accumulation of bacteria enhances the strength of transport barriers and highlights the role of understudied elliptical Lagrangian coherent structures in bacterial and multicomponent transport.

We investigate the effects of bacterial activity on the mixing and transport properties of a passive scalar in time-periodic flows in experiments and in a simple model. We focus on the interactions between swimming Escherichia coli and the Lagrangian coherent structures (LCSs) of the flow, which are computed from experimentally measured velocity fields. Experiments show that such interactions are non-trivial and can lead to transport barriers through which the scalar flux is significantly reduced. Using the Poincaré map, we show that these transport barriers coincide with the outermost members of elliptic LCSs known as Lagrangian vortex boundaries. Numerical simulations further show that elliptic LCSs can repel elongated swimmers and lead to swimmer depletion within Lagrangian coherent vortices. A simple mechanism shows that such depletion is due to the preferential alignment of elongated swimmers with the tangents of elliptic LCSs. Our results provide insights into understanding the transport of micro-organisms in complex flows with dynamical topological features from a Lagrangian viewpoint.

We use the entropy method to analyse the nonlinear dynamics and stability of a continuum kinetic model of an active nematic suspension. From the time evolution of the relative entropy, an energy-like quantity in the kinetic model, we derive a variational bound on relative entropy fluctuations that can be expressed in terms of orientational order parameters. From this bound we show isotropic suspensions are nonlinearly stable for sufficiently low activity, and derive upper bounds on spatiotemporal averages in the unstable regime that are consistent with fully nonlinear simulations. This work highlights the self-organising role of activity in particle suspensions, and places limits on how organised such systems can be.

Microorganisms are ubiquitous in nature and technology. They inhabit diverse environments, ranging from small river tributaries and lakes, to oceans, as well as wastewater treatment plants and food manufacturing. In many of these environments, microorganisms coexist with settling particles. Here, we investigate the effects of microbial activity (swimming E. coli) on the settling dynamics of passive colloidal particles using particle tracking methods. Our results reveal the existence of two distinct regimes in the correlation length scale ($L_u$) and the effective diffusivity of the colloidal particles ($D_{eff}$), with increasing bacterial concentration ($\phi _b$). At low $\phi _b$, the parameters $L_u$ and $D_{eff}$ increase monotonically with increasing $\phi _b$. Beyond critical $\phi _b$, a second regime is found where both $D_{eff}$ and $L_u$ are independent of $\phi _b$. We demonstrate that the transition between these regimes is characterized by the emergence of bioconvection. We use experimentally measured particle-scale quantities $L_u$ and $D_{eff}$ to predict the critical bacterial concentration for the diffusion–bioconvection transition.

In this paper, we explore the hydrodynamics of spheroidal active particles in viscosity gradients. This work provides a more accurate modelling approach, in comparison to spherical particles, for anisotropic organisms such as Paramecium swimming through inhomogeneous environments, but more fundamentally examines the influence of particle shape on viscotaxis. We find that spheroidal squirmers generally exhibit dynamics consistent with their spherical analogues, irrespective of the classification of swimmers as pushers, pullers or neutral swimmers. However, the slenderness of the spheroids tends to reduce the impact of viscosity gradients on their dynamics; when a swimmer becomes more slender, the viscosity difference across its body is reduced, which leads to slower reorientation. We also derive the mobility tensor for passive spheroids in viscosity gradients, generalizing previous results for spheres and slender bodies. This work enhances our understanding of how shape factors into the dynamics of passive and active particles in viscosity gradients, and offers new perspectives that could aid the control of both natural and synthetic swimmers in complex fluid environments.

The squirmer is a popular model to analyse the fluid mechanics of a self-propelled object, such as a micro-organism. We demonstrate that some fore–aft symmetric squirmers can spontaneously self-propel above a critical Reynolds number. Specifically, we numerically study the effects of inertia on spherical squirmers characterised by an axially and fore–aft symmetric ‘quadrupolar’ distribution of surface-slip velocity; under creeping-flow conditions, such squirmers generate a pure stresslet flow, the stresslet sign classifying the squirmer as either a ‘pusher’ or ‘puller’. Assuming axial symmetry, and over the examined range of the Reynolds number $Re$ (defined based upon the magnitude of the quadrupolar squirming), we find that spontaneous symmetry breaking occurs in the puller case above $Re \approx 14.3$, with steady swimming emerging from that threshold consistently with a supercritical pitchfork bifurcation and with the swimming speed growing monotonically with $Re$.

Over the last decade, substantial progress has been made in understanding the topology of quasi-two-dimensional (2-D) non-equilibrium fluid flows driven by ATP-powered microtubules and microorganisms. By contrast, the topology of three-dimensional (3-D) active fluid flows still poses interesting open questions. Here, we study the topology of a spherically confined active flow using 3-D direct numerical simulations of generalized Navier–Stokes (GNS) equations at the scale of typical microfluidic experiments. Consistent with earlier results for unbounded periodic domains, our simulations confirm the formation of Beltrami-like bulk flows with spontaneously broken chiral symmetry in this model. Furthermore, by leveraging fast methods to compute linking numbers, we explicitly connect this chiral symmetry breaking to the entanglement statistics of vortex lines. We observe that the mean of linking number distribution converges to the global helicity, consistent with the asymptotic result by Arnold [In Vladimir I. Arnold – Collected Works (ed. A.B. Givental, B.A. Khesin, A.N. Varchenko, V.A. Vassiliev & O.Y. Viro), pp. 357–375. Springer]. Additionally, we characterize the rate of convergence of this measure with respect to the number and length of observed vortex lines, and examine higher moments of the distribution. We find that the full distribution is well described by a k-Gamma distribution, in agreement with an entropic argument. Beyond active suspensions, the tools for the topological characterization of 3-D vector fields developed here are applicable to any solenoidal field whose curl is tangent to or cancels at the boundaries of a simply connected domain.

For dissolving active oil droplets in an ambient liquid, it is generally assumed that the Marangoni effect results in repulsive interactions, while the buoyancy effects caused by the density difference between the droplets, diffusing product and the ambient fluid are usually neglected. However, it has been observed in recent experiments that active droplets can form clusters due to buoyancy-driven convection (Krüger et al., Eur. Phys. J. E, vol. 39, 2016, pp. 1–9). In this study we numerically analyse the buoyancy effect, in addition to the propulsion caused by Marangoni flow (with its strength characterized by the Péclet number $Pe$). The buoyancy effects have their origin in (i) the density difference between the droplet and the ambient liquid, which is characterized by the Galileo number 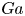$Ga$; and (ii) the density difference between the diffusing product (i.e. filled micelles) and the ambient liquid, which can be quantified by a solutal Rayleigh number $Ra$. We analyse how the attracting and repulsing behaviour of neighbouring droplets depends on the control parameters 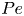$Pe$, 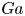$Ga$ and $Ra$. We find that while the Marangoni effect leads to the well-known repulsion between the interacting droplets, the buoyancy effect of the reaction product leads to buoyancy-driven attraction. At sufficiently large 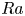$Ra$, even collisions between the droplets can take place. Our study on the effect of 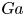$Ga$ further shows that with increasing 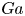$Ga$, the collision becomes delayed. Moreover, we derive that the attracting velocity of the droplets, which is characterized by a Reynolds number 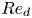$Re_d$, is proportional to 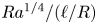$Ra^{1/4}/( \ell /R)$, where 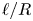$\ell /R$ is the distance between the neighbouring droplets normalized by the droplet radius. Finally, we numerically obtain the repulsive velocity of the droplets, characterized by a Reynolds number $Re_{rep}$, which is proportional to 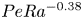$PeRa^{-0.38}$. The balance of attractive and repulsive effect leads to 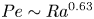$Pe\sim Ra^{0.63}$, which agrees well with the transition curve between the regimes with and without collision.

Spontaneous motion due to symmetry breaking has been predicted theoretically for both active droplets and isotropically active particles in an unbounded fluid domain, provided that their intrinsic Péclet number $Pe$ exceeds a critical value. However, due to their inherently small $Pe$, this phenomenon has yet to be observed experimentally for active particles. In this paper, we demonstrate theoretically that spontaneous motion for an active spherical particle closely fitting in a cylindrical channel is possible at arbitrarily small $Pe$. Scaling arguments in the limit where the dimensionless clearance is $\epsilon \ll 1$ reveal that when $Pe=O(\epsilon ^{1/2})$, the confined particle reaches speeds comparable to those achieved in an unbounded fluid at moderate (supercritical) $Pe$ values. We use matched asymptotic expansions in that distinguished limit, where the fluid domain decomposes into several asymptotic regions: a gap region, where the lubrication approximation applies; particle-scale regions, where the concentration is uniform; and far-field regions, where solute transport is one-dimensional. We derive an asymptotic formula for the particle speed, which is a monotonically decreasing function of $\overline {Pe}=Pe/\epsilon ^{1/2}$ and approaches a finite limit as $\overline {Pe}\searrow 0$. Our results could pave the way for experimental realisations of symmetry-breaking spontaneous motion in active particles.

Motile bacteria play essential roles in biology that rely on their dynamic behaviours, including their ability to navigate, interact and self-organize. However, bacteria dynamics on fluid interfaces are not well understood. Swimmers adsorbed on fluid interfaces remain highly motile, and fluid interfaces are highly non-ideal domains that alter swimming behaviour. To understand these effects, we study flow fields generated by Pseudomonas aeruginosa PA01 in the pusher mode. Analysis of correlated displacements of tracers and bacteria reveals dipolar flow fields with unexpected asymmetries that differ significantly from their counterparts in bulk fluids. We decompose the flow field into fundamental hydrodynamic modes for swimmers in incompressible fluid interfaces. We find an expected force-doublet mode corresponding to propulsion and drag at the interface plane, and a second dipolar mode, associated with forces exerted by the flagellum on the cell body in the aqueous phase that are countered by Marangoni stresses in the interface. The balance of these modes depends on the bacteria's trapped interfacial configurations. Understanding these flows is broadly important in nature and in the design of biomimetic swimmers.