No CrossRef data available.
Article contents
Crowding accelerates the rotation of a bacterial rotor
Published online by Cambridge University Press: 18 September 2024
Abstract
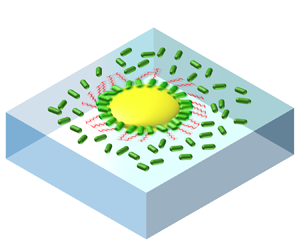
Understanding the propulsion of a swimmer in a large group of individuals holds the key to unravelling the intriguing dynamics of active matter collective motion. Here, we develop a two-dimensional (2-D) self-assembled rotor, powered by bacterial flagella. At a water–air interface, the average direction of rotation of a rotor is fixed. When the chiral rotor is put into a 2-D bacterial suspension, we examine the average and fluctuation of the angular velocity of the rotor. Remarkably, the average angular velocity of a rotor is found to increase up to 3 times when the density of surrounding bacterial suspension increases and the increase is nonlinear. In a dense suspension of bacteria, the existence of a rotor disrupts vortices in the surrounding active turbulence, and the acceleration of the rotor is independent of the activity level of the surrounding free bacteria. The nonlinear acceleration thus results from hydrodynamic interaction with surrounding crowdedness that can be quantitatively explained by hydrodynamic simulation. The simultaneity between the acceleration of rotor and free bacteria in active turbulence suggests that crowding-induced acceleration may promote the onset of instability. The result will inspire new active-matter-based microfluidic devices with improved transport properties.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press


