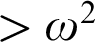 ${>}\ \omega ^2$
-Fickle Recursively Enumerable Turing Degrees
${>}\ \omega ^2$
-Fickle Recursively Enumerable Turing Degrees
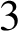 $3$
-MANIFOLDS IN
$3$
-MANIFOLDS IN
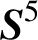 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$