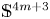 $\mathbb {S}^{4m+3}$ as the principal orbit
$\mathbb {S}^{4m+3}$ as the principal orbit
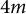 $4m$
-manifolds
$4m$
-manifolds
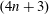 $(4n+3)$-dimensional Spheres
$(4n+3)$-dimensional Spheres