Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T13:12:19.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical Approximations to Extremal Toric Kähler Metrics with Arbitrary Kähler Class

Part of: Global differential geometry Partial differential equations, boundary value problems

Published online by Cambridge University Press:  10 January 2017

Stuart James Hall  and
Thomas Murphy
Stuart James Hall
Affiliation:
Department of Applied Computing, University of Buckingham, Hunter Street, Buckingham MK18 1EG, UK
Thomas Murphy
Affiliation:
Department of Mathematics, California State University Fullerton, 800 N. State College Boulevard, Fullerton, CA 92831, USA (tmurphy@fullerton.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop new algorithms for approximating extremal toric Kähler metrics. We focus on an extremal metric on 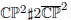, which is conformal to an Einstein metric (the Chen–LeBrun–Weber metric). We compare our approximation to one given by Bunch and Donaldson and compute various geometric quantities. In particular, we demonstrate a small eigenvalue of the scalar Laplacian of the Einstein metric that gives numerical evidence that the Einstein metric is conformally unstable under Ricci flow.

Keywords

extremal Kähler metricEinstein metricRicci flowlinear stability

MSC classification

Secondary: 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.) 53C55: Hermitian and Kählerian manifolds 65N35: Spectral, collocation and related methods
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 60 , Issue 4 , November 2017 , pp. 893 - 910
Copyright
Copyright © Edinburgh Mathematical Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abreu, M., Kähler geometry of toric varieties and extremal metrics, Int. J. Math. 9(6) (1998), 641–651.CrossRefGoogle Scholar
2. Abreu, M., Kähler geometry of toric manifolds in symplectic coordinates, Fields Institute Communications, Volume 35, pp. 1–24 (American Mathematical Society, Providence, RI, 2003).Google Scholar
3. Braun, V., Brelidze, T., Douglas, M. R. and Ovrut, B. A., Eigenvalues and eigenfunctions of the scalar Laplace operator on Calabi–Yau manifolds, J. High Energy Phys. 2008 (2008), article 120.Google Scholar
4. Bunch, R. S. and Donaldson, S. K., Numerical approximations to extremal metrics on toric surfaces, in Handbook of geometric analysis, Advanced Lectures in Mathematics, Volume 7, Number 1, pp. 1–28 (International Press, 2008).Google Scholar
5. Calabi, E., Extremal Kähler metrics, Annals of Mathematics Studies, Volume 102, pp. 259–290 (Princeton University Press, 1982).Google Scholar
6. Cao, H.-D. and Chenxu, H., Linear stability of Perelman's ν-entropy on symmetric spaces of compact type, J. Reine Angew. Math. 353(3) (2015), 229–246.CrossRefGoogle Scholar
7. Cao, H.-D. and Zhu, M., On second variation of Perelman's shrinker entropy, Math. Ann. 353(3) (2012), 747–763.Google Scholar
8. Cao, H.-D., Hamilton, R. and Ilmanen, T., Gaussian density and stability for some Ricci solitons, Preprint (arXiv:0404.165; 2004).Google Scholar
9. Chen, X. X., LeBrun, C. and Weber, B., On conformally Kähler, Einstein manifolds, J. Am. Math. Soc. 21(4) (2008), 1137–1168.Google Scholar
10. Derdzinski, A., Self-dual Kähler manifolds and Einstein manifolds of dimension four, Compositio Math. 49 (1983), 405–433.Google Scholar
11. Donaldson, S. K., Interior estimates for solutions of Abreu's equation, Collectanea Math. 56(2) (2005), 103–142.Google Scholar
12. Donaldson, S. K., Kähler geometry on toric manifolds and some other manifolds with large symmetry, in Handbook of geometric analysis, Advanced Lectures in Mathematics, Volume 7, Number 1, pp. 29–75 (International Press, 2008).Google Scholar
13. Donaldson, S. K., Some numerical results in complex differential geometry, Pure Appl. Math. Q. 5(2) (2009), 571–618.Google Scholar
14. Doran, C., Headrick, M., Herzog, C., Kantor, J. and Wiseman, T., Numerical Kähler–Einstein on the third del Pezzo, Commun. Math. Phys. 282(2) (2008), 357–393.Google Scholar
15. Flannery, B. P., Press, W. H., Teukolsky, S. A. and Vetterling, W. T., Numerical recipes: the art of scientific computing, 3rd edn (Cambridge University Press, 2007).Google Scholar
16. Gibbons, G. and Hartnoll, S., Graviational instability in higher dimensions, Phys. Rev. D66 (2002), 24–64.Google Scholar
17. Guillemin, V., Kähler structures on toric varieties, J. Diff. Geom. 40(2) (1994), 285–309.Google Scholar
18. Hall, S. J. and Murphy, T., On the spectrum of the Page and Chen–LeBrun–Weber metrics, Annals Global Analysis Geom. 46(1) (2014), 87–101.Google Scholar
19. Hall, S. J. and Murphy, T., Approximating Ricci solitons and quasi-Einstein metrics on toric surfaces, New York J. Math. 22 (2016), 615–635.Google Scholar
20. Hall, S. J., Haslhofer, R. and Siepmann, M., The stability inequality for Ricci-flat cones, J. Geom. Analysis 24(1) (2014), 472–494.CrossRefGoogle Scholar
21. Headrick, M. and Nassar, A., Energy functionals and Calabi–Yau metrics, Adv. Theor. Math. Phys. 17 (2013), 867–902.CrossRefGoogle Scholar
22. Headrick, M. and Wiseman, T., Numerical Ricci-flat metrics on K3, Class. Quant. Grav. 22(3) (2005), 4931–4960.Google Scholar
23. Headrick, M. and Wiseman, T., Numerical Kähler–Ricci soliton on the second del Pezzo, Preprint (arXiv:0706.2329v1; 2007).Google Scholar
24. Keller, J., Ricci iterations on Kähler classes, J. Inst. Math. Jussieu 8(4) (2009), 743–768.Google Scholar
25. LeBrun, C., Einstein metrics on complex surfaces, in Geometry and Physics, Aarhus, 1995 (ed. Pedersen, H., Andersen, J., Dupont, J. and Swann, A.), Lecture Notes in Pure and Applied Mathematics, Volume jt, pp. 167–176 (Marcel Dekker, New York, 1997).Google Scholar
26. LeBrun, C., On Einstein Hermitian 4-manifolds, J. Diff. Geom. 90 (2012), 277–302.Google Scholar
27. Page, D., A compact rotating gravitational instanton, Phys. Lett. B79 (1979), 235–238.CrossRefGoogle Scholar
28. Perelman, G., The entropy formula for the Ricci flow and its geometric applications, Preprint (arXiv:math/0211159v1; 2002).Google Scholar
29. Young, R. E., Semiclassical instability of gravity with positive cosmological constant, Phys. Rev. D28(10) (1983), 2436–2438.Google Scholar