Refine search
Actions for selected content:
47 results
Mechanical loads from simulated lightning strike on protected carbon fibre-reinforced polymers revisited: implementation and experimental validation
-
- Journal:
- The Aeronautical Journal , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytical and numerical validation of a plate–plate tribometer for measuring wall slip
- Part of
-
- Journal:
- Flow: Applications of Fluid Mechanics / Volume 4 / 2024
- Published online by Cambridge University Press:
- 17 December 2024, E31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Numerical modelling of dense snow avalanches with a well-balanced scheme based on the 2D shallow water equations
-
- Journal:
- Journal of Glaciology / Volume 69 / Issue 278 / December 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 1646-1662
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GP-MOOD: a positivity-preserving high-order finite volume method for hyperbolic conservation laws
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 16 / Issue S362 / June 2020
- Published online by Cambridge University Press:
- 20 January 2023, pp. 373-379
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
NUMERICAL ENTROPY PRODUCTION AS SMOOTHNESS INDICATOR FOR SHALLOW WATER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 28 November 2019, pp. 398-415
-
- Article
-
- You have access
- Export citation
Development of a Parallel Explicit Finite-Volume Euler Equation Solver using the Immersed Boundary Method with Hybrid MPI-CUDA Paradigm
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 11 October 2019, pp. 87-102
- Print publication:
- February 2020
-
- Article
- Export citation
Forced Convection Enhancement Over Heated Blocks by Using Slot-Jet
-
- Journal:
- Journal of Mechanics / Volume 36 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 23 September 2019, pp. 119-131
- Print publication:
- February 2020
-
- Article
- Export citation
Application of Response Surface Methodology in the Optimization of Magneto-Hydrodynamic Flow Around and Through a Porous Circular Cylinder
-
- Journal:
- Journal of Mechanics / Volume 34 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 08 February 2018, pp. 695-710
- Print publication:
- October 2018
-
- Article
- Export citation
A Dispersive Numerical Model for the Formation of Undular Bores Generated by Tsunami Wave Fission
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 767-784
- Print publication:
- November 2017
-
- Article
- Export citation
A Third Order Adaptive ADER Scheme for One Dimensional Conservation Laws
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 829-851
- Print publication:
- September 2017
-
- Article
- Export citation
Finite Volume Method for Pricing European and American Options under Jump-Diffusion Models
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 227-247
- Print publication:
- May 2017
-
- Article
- Export citation
Admissible Regions for Higher-Order Finite Volume Method Grids
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 269-285
- Print publication:
- May 2017
-
- Article
- Export citation
Finite Volume Lattice Boltzmann Method for Nearly Incompressible Flows on Arbitrary Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 301-324
- Print publication:
- August 2016
-
- Article
- Export citation
Osher Flux with Entropy Fix for Two-Dimensional Euler Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 670-692
- Print publication:
- August 2016
-
- Article
- Export citation
Divergence-Free WENO Reconstruction-Based Finite Volume Scheme for Solving Ideal MHD Equations on Triangular Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 841-880
- Print publication:
- April 2016
-
- Article
- Export citation
High-Order Finite Volume Methods for Aerosol Dynamic Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 27 January 2016, pp. 213-235
- Print publication:
- April 2016
-
- Article
- Export citation
Optimal Bicubic Finite Volume Methods on Quadrilateral Meshes
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 7 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 29 May 2015, pp. 454-471
- Print publication:
- August 2015
-
- Article
- Export citation
Momentum Conservative Schemes for Shallow Water Flows
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 4 / Issue 2 / May 2014
- Published online by Cambridge University Press:
- 28 May 2015, pp. 152-165
- Print publication:
- May 2014
-
- Article
- Export citation
A Geometry-Preserving Finite Volume Method for Compressible Fluids on Schwarzschild Spacetime
-
- Journal:
- Communications in Computational Physics / Volume 15 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 03 June 2015, pp. 827-852
- Print publication:
- March 2014
-
- Article
- Export citation
Kinetic Energy Preserving and Entropy Stable Finite Volume Schemes for Compressible Euler and Navier-Stokes Equations
-
- Journal:
- Communications in Computational Physics / Volume 14 / Issue 5 / November 2013
- Published online by Cambridge University Press:
- 03 June 2015, pp. 1252-1286
- Print publication:
- November 2013
-
- Article
- Export citation





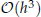 convergence rate in
convergence rate in 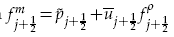 where
where 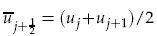 and
and 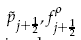 are
are 