Many problems in combinatorial linear algebra require upper bounds on the number of solutions to an underdetermined system of linear equations $Ax = b$, where the coordinates of the vector x are restricted to take values in some small subset (e.g. $\{\pm 1\}$) of the underlying field. The classical ways of bounding this quantity are to use either a rank bound observation due to Odlyzko or a vector anti-concentration inequality due to Halász. The former gives a stronger conclusion except when the number of equations is significantly smaller than the number of variables; even in such situations, the hypotheses of Halász’s inequality are quite hard to verify in practice. In this paper, using a novel approach to the anti-concentration problem for vector sums, we obtain new Halász-type inequalities that beat the Odlyzko bound even in settings where the number of equations is comparable to the number of variables. In addition to being stronger, our inequalities have hypotheses that are considerably easier to verify. We present two applications of our inequalities to combinatorial (random) matrix theory: (i) we obtain the first non-trivial upper bound on the number of $n\times n$ Hadamard matrices and (ii) we improve a recent bound of Deneanu and Vu on the probability of normality of a random $\{\pm 1\}$ matrix.

In this paper, we give general recommendations for successful application of the Douglas–Rachford reflection method to convex and nonconvex real matrix completion problems. These guidelines are demonstrated by various illustrative examples.

We prove an upper bound on sums of squares of minors of 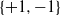$\{+1, -1\}$-matrices. The bound is sharp for Hadamard matrices, a result due to de Launey and Levin [‘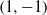$(1,-1)$-matrices with near-extremal properties’, SIAM J. Discrete Math.23(2009), 1422–1440], but our proof is simpler. We give several corollaries relevant to minors of Hadamard matrices.