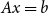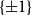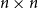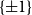1. Introduction
1.1. The number of Hadamard matrices
A square matrix H of order n whose entries are
![]() $\{\pm{1}\}$
is called a Hadamard matrix of order n if its rows are pairwise orthogonal, i.e. if
$\{\pm{1}\}$
is called a Hadamard matrix of order n if its rows are pairwise orthogonal, i.e. if
![]() $ HH^{T} = nI_{n}$
. These matrices are named after Jacques Hadamard, who studied them in connection with his maximal determinant problem. Specifically, Hadamard asked for the maximum value of the determinant of any
$ HH^{T} = nI_{n}$
. These matrices are named after Jacques Hadamard, who studied them in connection with his maximal determinant problem. Specifically, Hadamard asked for the maximum value of the determinant of any
![]() $n \times n$
square matrix all of whose entries are bounded in absolute value by 1. He proved [Reference HadamardHad93] that the value of the determinant of such matrices cannot exceed
$n \times n$
square matrix all of whose entries are bounded in absolute value by 1. He proved [Reference HadamardHad93] that the value of the determinant of such matrices cannot exceed
![]() $n^{n/2}$
. Moreover, he showed that Hadamard matrices are the only ones that can attain this bound. Since their introduction, Hadamard matrices have been the focus of considerable attention from many different communities – coding theory, design theory, statistical inference and signal processing to name a few. We refer the reader to the surveys [Reference Hedayat and WallisHW+78, Reference Seberry and YamadaSY92] and the books [Reference AgaianAga06, Reference HoradamHor12] for a comprehensive account of Hadamard matrices and their numerous applications.
$n^{n/2}$
. Moreover, he showed that Hadamard matrices are the only ones that can attain this bound. Since their introduction, Hadamard matrices have been the focus of considerable attention from many different communities – coding theory, design theory, statistical inference and signal processing to name a few. We refer the reader to the surveys [Reference Hedayat and WallisHW+78, Reference Seberry and YamadaSY92] and the books [Reference AgaianAga06, Reference HoradamHor12] for a comprehensive account of Hadamard matrices and their numerous applications.
Hadamard matrices of order 1 and 2 are trivial to construct, and it is quite easy to see, by considering the first few rows, that every other Hadamard matrix (if exists) must be of order 4m for some
![]() $m\in \mathbb{N}$
. Whereas Hadamard matrices of infinitely many orders have been constructed, the question of whether one of order 4m exists for every
$m\in \mathbb{N}$
. Whereas Hadamard matrices of infinitely many orders have been constructed, the question of whether one of order 4m exists for every
![]() $m\in \mathbb{N}$
is the most important open question on this topic and remains wide open.
$m\in \mathbb{N}$
is the most important open question on this topic and remains wide open.
Conjecture 1.1 (The Hadamard conjecture, [Reference PaleyPal33]). There exists a Hadamard matrix of order 4m for every
![]() $m\in \mathbb{N}$
.
$m\in \mathbb{N}$
.
In this paper, we study the question of how many Hadamard matrices of order
![]() $n=4m$
could possibly exist for a given
$n=4m$
could possibly exist for a given
![]() $m\in \mathbb{N}$
. Let us denote this number by H(n). Note that if a single Hadamard matrix of order n exists, then we immediately get at least
$m\in \mathbb{N}$
. Let us denote this number by H(n). Note that if a single Hadamard matrix of order n exists, then we immediately get at least
![]() $n!$
distinct Hadamard matrices by permuting its rows. Thus, if the Hadamard conjecture is true, then
$n!$
distinct Hadamard matrices by permuting its rows. Thus, if the Hadamard conjecture is true, then
![]() $H(n) = 2^{\Omega( n\log{n})}$
for every
$H(n) = 2^{\Omega( n\log{n})}$
for every
![]() $n=4m, m\in \mathbb{N}$
. On the other hand, the bound
$n=4m, m\in \mathbb{N}$
. On the other hand, the bound
![]() $H(n) \leq 2^{\binom{n+1}{2}}$
is quite easy to obtain, as we will discuss in the next subsection.
$H(n) \leq 2^{\binom{n+1}{2}}$
is quite easy to obtain, as we will discuss in the next subsection.
This bound also appeared in the work of de Launey and Levin [Reference De Launey and LevinDLL10] on the enumeration of partial Hadamard matrices (i.e.
![]() $k\times 4m$
matrices whose rows are pairwise orthogonal, in the limit as
$k\times 4m$
matrices whose rows are pairwise orthogonal, in the limit as
![]() $m\to \infty$
) using Fourier analytic techniques; notably, while they were able to get a very precise answer to this problem (up to an overall
$m\to \infty$
) using Fourier analytic techniques; notably, while they were able to get a very precise answer to this problem (up to an overall
![]() $(1+o(1))$
multiplicative factor), their techniques still did not help them to obtain anything better than the essentially trivial bound for the case of square Hadamard matrices. As our first main result, we give the only known non-trivial upper bound on the number of square Hadamard matrices.
$(1+o(1))$
multiplicative factor), their techniques still did not help them to obtain anything better than the essentially trivial bound for the case of square Hadamard matrices. As our first main result, we give the only known non-trivial upper bound on the number of square Hadamard matrices.
Theorem 1.2. There exists an absolute constant
![]() $c_H > 0$
such that
$c_H > 0$
such that
![]() $H(n)\leq 2^{\frac{(1-c_H)n^2}{2}}$
for all sufficiently large n that is a multiple of 4.
$H(n)\leq 2^{\frac{(1-c_H)n^2}{2}}$
for all sufficiently large n that is a multiple of 4.
Remark. In our proof of the above theorem, we have focused on the simplicity and clarity of presentation and have made no attempt to optimize this constant. In any case, our proof cannot give a value of
![]() $c_H$
larger than (say)
$c_H$
larger than (say)
![]() $\frac{1}{2}$
, which we believe is quite far from the truth. More precisely, we make the following conjecture.
$\frac{1}{2}$
, which we believe is quite far from the truth. More precisely, we make the following conjecture.
Conjecture 1.3. For any
![]() $n=4m, m\in \mathbb{N}$
,
$n=4m, m\in \mathbb{N}$
,
![]() $H(n) = 2^{O(n\log{n})}$
.
$H(n) = 2^{O(n\log{n})}$
.
We believe that proving a bound of the form
![]() $H(n) = 2^{o(n^2)}$
will already be very interesting and will likely require new ideas.
$H(n) = 2^{o(n^2)}$
will already be very interesting and will likely require new ideas.
1.1.1 The approach
We now discuss the proof of the trivial upper bound
![]() $H(n) \leq 2^{\binom{n+1}{2}}$
. The starting point is the following classical (and almost trivial to prove) observation due to Odlyzko.
$H(n) \leq 2^{\binom{n+1}{2}}$
. The starting point is the following classical (and almost trivial to prove) observation due to Odlyzko.
Lemma 1.4 (Odlyzko, [Reference OdlyzkoOdl88]). Let W be a d-dimensional subspace of
![]() $\mathbb{R}^n$
. Then,
$\mathbb{R}^n$
. Then,
![]() $|W\cap \{\pm1\}^n|\leq 2^d$
.
$|W\cap \{\pm1\}^n|\leq 2^d$
.
Sketch. As W is a d-dimensional space, it depends only on d coordinates. Therefore, it spans at most
![]() $2^d$
vectors with entries from
$2^d$
vectors with entries from
![]() $\{\pm1\}$
.
$\{\pm1\}$
.
The bound
![]() $H(n) \leq 2^{\binom{n+1}{2}}$
is now immediate. Indeed, we construct the matrices row by row and note that by the orthogonality of the rows, the first k rows span a subspace of dimension k to which the remaining rows are orthogonal. In particular, once the first k rows have been selected, the
$H(n) \leq 2^{\binom{n+1}{2}}$
is now immediate. Indeed, we construct the matrices row by row and note that by the orthogonality of the rows, the first k rows span a subspace of dimension k to which the remaining rows are orthogonal. In particular, once the first k rows have been selected, the
![]() $(k+1)^{st}$
row lies in a specified subspace of dimension
$(k+1)^{st}$
row lies in a specified subspace of dimension
![]() $n-k$
(the orthogonal complement of the vector space spanned by the first k (linearly independent) rows), and hence, by Lemma 1.4, is one of at most
$n-k$
(the orthogonal complement of the vector space spanned by the first k (linearly independent) rows), and hence, by Lemma 1.4, is one of at most
![]() $2^{n-k}$
vectors. It follows that
$2^{n-k}$
vectors. It follows that
![]() $H(n) \leq \prod_{i=0}^{n-1}2^{n-i} = 2^{\binom{n+1}{2}}$
.
$H(n) \leq \prod_{i=0}^{n-1}2^{n-i} = 2^{\binom{n+1}{2}}$
.
The weak point in the above proof is the following – while Odlyzko’s bound is tight in general, we should expect it to be far from the truth in the average case. Indeed, working with vectors in
![]() $\{0,1\}^{n}$
for the moment, note that a subspace of dimension k spanned by vectors in
$\{0,1\}^{n}$
for the moment, note that a subspace of dimension k spanned by vectors in
![]() $\{0,1\}^{n}$
has exactly
$\{0,1\}^{n}$
has exactly
![]() $2^{n-k}$
vectors in
$2^{n-k}$
vectors in
![]() $\{0,1\}^{n}$
orthogonal to it viewed as elements of
$\{0,1\}^{n}$
orthogonal to it viewed as elements of
![]() $\mathbb{F}_{2}^{n}$
. However, typically, the inner products will take on many values in
$\mathbb{F}_{2}^{n}$
. However, typically, the inner products will take on many values in
![]() $2\mathbb{Z} \setminus \{0\}$
so that many of these vectors will not be orthogonal viewed as elements of
$2\mathbb{Z} \setminus \{0\}$
so that many of these vectors will not be orthogonal viewed as elements of
![]() $\mathbb{R}^{n}$
.
$\mathbb{R}^{n}$
.
The study of the difference between the Odlyzko bound and how many
![]() $\{\pm 1\}^{n}$
vectors a subspace actually contains has been very fruitful in discrete random matrix theory, particularly for the outstanding problem of determining the probability of singularity of random
$\{\pm 1\}^{n}$
vectors a subspace actually contains has been very fruitful in discrete random matrix theory, particularly for the outstanding problem of determining the probability of singularity of random
![]() $\{\pm 1\}$
matrices. Following Kahn, Komlós and Szemerédi [Reference Kahn, Komlós and SzemerédiKKS95], Tao and Vu [Reference Terence and VanTV07] isolated the following notion.
$\{\pm 1\}$
matrices. Following Kahn, Komlós and Szemerédi [Reference Kahn, Komlós and SzemerédiKKS95], Tao and Vu [Reference Terence and VanTV07] isolated the following notion.
Definition 1.5 (Combinatorial dimension). The combinatorial dimension of a subspace W in
![]() $\mathbb{R}^n$
, denoted by
$\mathbb{R}^n$
, denoted by
![]() $d_{\pm}(W)$
, is defined to be smallest real number such that
$d_{\pm}(W)$
, is defined to be smallest real number such that
Thus, Odlyzko’s lemma says that for any subspace W, its combinatorial dimension is no more than its dimension. However, improving on another result of Odlyzko [Reference OdlyzkoOdl88], Kahn, Komlós and Szemerédi showed that this bound is very loose for typical subspaces spanned by
![]() $\{\pm 1\}^{n}$
vectors:
$\{\pm 1\}^{n}$
vectors:
Theorem 1.6 (Kahn-Komlós-Szemeríi, [Reference Kahn, Komlós and SzemerédiKKS95]). There exists a constant
![]() $C>0$
such that if
$C>0$
such that if
![]() $r\leq n-C$
, and if
$r\leq n-C$
, and if
![]() $v_{1},\dots,v_{r}$
are chosen independently and uniformly from
$v_{1},\dots,v_{r}$
are chosen independently and uniformly from
![]() $\{\pm1\}^{n}$
, then
$\{\pm1\}^{n}$
, then
In other words, they showed that a typical r-dimensional subspace spanned by r vectors in
![]() $\{\pm 1\}^{n}$
contains the minimum possible number of
$\{\pm 1\}^{n}$
contains the minimum possible number of
![]() $\{\pm 1\}^{n}$
vectors, i.e. only the 2r vectors consisting of the vectors spanning the subspace and their negatives.
$\{\pm 1\}^{n}$
vectors, i.e. only the 2r vectors consisting of the vectors spanning the subspace and their negatives.
Compared to the setting of Kahn, Komlós and Szemerédi, our setting has two major differences:
-
(i) We are interested not in the combinatorial dimension of subspaces spanned by
 $\{\pm 1\}^{n}$
vectors but of their orthogonal complements.
$\{\pm 1\}^{n}$
vectors but of their orthogonal complements. -
(ii) The
 $\{\pm 1\}^{n}$
vectors spanning a subspace in our case are highly dependent due to the mutual orthogonality constraint – indeed, as the proof of the trivial upper bound at the start of the subsection shows, the probability that the rows of a random
$\{\pm 1\}^{n}$
vectors spanning a subspace in our case are highly dependent due to the mutual orthogonality constraint – indeed, as the proof of the trivial upper bound at the start of the subsection shows, the probability that the rows of a random
 $k \times n$
$k \times n$
 $\{\pm1\}$
matrix are mutually orthogonal is
$\{\pm1\}$
matrix are mutually orthogonal is
 $2^{-\Omega(k^{2})}$
; this rules out the strategy of conditioning on the rows being orthogonal when
$2^{-\Omega(k^{2})}$
; this rules out the strategy of conditioning on the rows being orthogonal when
 $k=\Omega(\sqrt{n})$
, even if one were to prove a variant of the result of Kahn, Komlós and Szemerédi to deal with orthogonal complements.
$k=\Omega(\sqrt{n})$
, even if one were to prove a variant of the result of Kahn, Komlós and Szemerédi to deal with orthogonal complements.
Briefly, our approach to dealing with these obstacles is the following. For
![]() $k<n$
, let
$k<n$
, let
![]() $H_{k,n}$
denote a
$H_{k,n}$
denote a
![]() $k\times n$
matrix with all its entries in
$k\times n$
matrix with all its entries in
![]() $\{\pm 1\}$
and all of whose rows are orthogonal. We will show that there exist absolute constants
$\{\pm 1\}$
and all of whose rows are orthogonal. We will show that there exist absolute constants
![]() $0< c_1 < c_2 < 1$
such that if
$0< c_1 < c_2 < 1$
such that if
![]() $k\in [c_1 n, c_2 n]$
and if n is sufficiently large, then
$k\in [c_1 n, c_2 n]$
and if n is sufficiently large, then
![]() $H_{k,n}$
must have a certain desirable linear algebraic property, namely that there are at least
$H_{k,n}$
must have a certain desirable linear algebraic property, namely that there are at least
![]() $C(c_1,c_2)$
disjoint submatrices of rank at least cn; this is the only way in which we use the orthogonality of the rows of
$C(c_1,c_2)$
disjoint submatrices of rank at least cn; this is the only way in which we use the orthogonality of the rows of
![]() $H_{k,n}$
and takes care of (ii). Next, to deal with (i), we will show that for any
$H_{k,n}$
and takes care of (ii). Next, to deal with (i), we will show that for any
![]() $k\times n$
matrix A which has this linear algebraic structure, the number of solutions x in
$k\times n$
matrix A which has this linear algebraic structure, the number of solutions x in
![]() $\{\pm 1\}^{n}$
to
$\{\pm 1\}^{n}$
to
![]() $Ax=0$
is at most
$Ax=0$
is at most
![]() $2^{n-(1+C)k}$
, where
$2^{n-(1+C)k}$
, where
![]() $C>0$
is a constant depending only on
$C>0$
is a constant depending only on
![]() $c_1$
and
$c_1$
and
![]() $c_2$
. Using these improved bounds with the same strategy as for the trivial proof, we see that for n sufficiently large,
$c_2$
. Using these improved bounds with the same strategy as for the trivial proof, we see that for n sufficiently large,
 \begin{align}H(n) & \leq \prod_{i=0}^{n-1}2^{n-i}\prod_{k=c_{1}n}^{c_{2}n}2^{-Ck} \nonumber \\ & \leq 2^{\big(\scriptsize\begin{array}{c} n+1\\[-2pt] 2\end{array}\big)}2^{-\frac{C(c_{2}^{2}-c_{1}^{2})n^{2}}{2}},\end{align}
\begin{align}H(n) & \leq \prod_{i=0}^{n-1}2^{n-i}\prod_{k=c_{1}n}^{c_{2}n}2^{-Ck} \nonumber \\ & \leq 2^{\big(\scriptsize\begin{array}{c} n+1\\[-2pt] 2\end{array}\big)}2^{-\frac{C(c_{2}^{2}-c_{1}^{2})n^{2}}{2}},\end{align}
which gives the desired improvement. We discuss this in more detail in the next subsection.
1.2. Improved Halász-type inequalities
As mentioned above, our goal is to study the number of
![]() $\{\pm 1\}^{n}$
solutions to an underdetermined system of linear equations
$\{\pm 1\}^{n}$
solutions to an underdetermined system of linear equations
![]() $Ax = 0$
possessing some additional structure. This question was studied by Halász, who proved the following:
$Ax = 0$
possessing some additional structure. This question was studied by Halász, who proved the following:
Theorem 1.7 (Halász, [Reference HalászHal77]). Let
![]() $a_1,\dots, a_n$
be a collection of vectors in
$a_1,\dots, a_n$
be a collection of vectors in
![]() $\mathbb{R}^d$
. Suppose there exists a constant
$\mathbb{R}^d$
. Suppose there exists a constant
![]() $\delta > 0$
such that for any unit vector
$\delta > 0$
such that for any unit vector
![]() $e\in \mathbb{R}^d$
, one can select at least
$e\in \mathbb{R}^d$
, one can select at least
![]() $\delta n$
vectors
$\delta n$
vectors
![]() $a_k$
with
$a_k$
with
![]() $|\langle a_k, e\rangle | \geq 1$
. Then,
$|\langle a_k, e\rangle | \geq 1$
. Then,
 \begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{2}< 1\right]\leq c(\delta,d)\left(\frac{1}{\sqrt{n}}\right)^{d},\end{equation*}
\begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{2}< 1\right]\leq c(\delta,d)\left(\frac{1}{\sqrt{n}}\right)^{d},\end{equation*}
where
![]() $\epsilon_1,\dots,\epsilon_n$
are independent Rademacher random variables, i.e. they take the values
$\epsilon_1,\dots,\epsilon_n$
are independent Rademacher random variables, i.e. they take the values
![]() $\pm 1$
with probability
$\pm 1$
with probability
![]() $1/2$
each.
$1/2$
each.
The constant
![]() $c(\delta, d)$
, which is crucial for our applications, was left implicit by Halász. However, explicit estimates on this constant may be obtained. Tao and Vu showed that the dependence on
$c(\delta, d)$
, which is crucial for our applications, was left implicit by Halász. However, explicit estimates on this constant may be obtained. Tao and Vu showed that the dependence on
![]() $\delta$
is
$\delta$
is
![]() $\delta^{-d/2}$
. More precisely,
$\delta^{-d/2}$
. More precisely,
Theorem 1.8 ([Reference Tao and VuTV12]). Let
![]() $a_1,\dots, a_n$
be a collection of vectors in
$a_1,\dots, a_n$
be a collection of vectors in
![]() $\mathbb{R}^d$
. Suppose that there exists some
$\mathbb{R}^d$
. Suppose that there exists some
![]() $m\in\mathbb{N}$
such that for every unit vector
$m\in\mathbb{N}$
such that for every unit vector
![]() $e\in\mathbb{R}^{d}$
, one can select at least m vectors
$e\in\mathbb{R}^{d}$
, one can select at least m vectors
![]() $a_{i_{1}},\dots,a_{i_{m}}$
with
$a_{i_{1}},\dots,a_{i_{m}}$
with
![]() $|\langle a_{i_{j}},e\rangle|\geq 1$
for all
$|\langle a_{i_{j}},e\rangle|\geq 1$
for all
![]() $j\in[m]$
. Then,
$j\in[m]$
. Then,
 \begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{2}< 1\right]\leq c(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
\begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{2}< 1\right]\leq c(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
where
![]() $\epsilon_1,\dots, \epsilon_n$
are i.i.d. Rademacher random variables.
$\epsilon_1,\dots, \epsilon_n$
are i.i.d. Rademacher random variables.
As for the dependence of d, an estimate is available in unpublished notes of Howard (following Oskolkov) [How].
Theorem 1.9 ([How]). Let
![]() $a_1,\dots, a_n$
be a collection of vectors in
$a_1,\dots, a_n$
be a collection of vectors in
![]() $\mathbb{R}^d$
. Suppose that there exists some
$\mathbb{R}^d$
. Suppose that there exists some
![]() $m\in\mathbb{N}$
such that for every unit vector
$m\in\mathbb{N}$
such that for every unit vector
![]() $e\in\mathbb{R}^{d}$
, one can select at least m vectors
$e\in\mathbb{R}^{d}$
, one can select at least m vectors
![]() $a_{i_{1}},\dots,a_{i_{m}}$
with
$a_{i_{1}},\dots,a_{i_{m}}$
with
![]() $|\langle a_{i_{j}},e\rangle|\geq1/(2\sqrt{d})$
for all
$|\langle a_{i_{j}},e\rangle|\geq1/(2\sqrt{d})$
for all
![]() $j\in[m]$
. Then,
$j\in[m]$
. Then,
 \begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{\infty}<\frac{1}{2}\right]\leq C(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
\begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{\infty}<\frac{1}{2}\right]\leq C(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
where
![]() $C(d)=\left(\frac{\pi^{3/2}d}{\sqrt{2}}\right)^{d}$
.
$C(d)=\left(\frac{\pi^{3/2}d}{\sqrt{2}}\right)^{d}$
.
Remark. This theorem implies Theorem 1.8 since the hypotheses are weaker and the conclusion is stronger (the origin centred
![]() $\ell_{2}$
-ball of radius 1 is contained in the origin centred
$\ell_{2}$
-ball of radius 1 is contained in the origin centred
![]() $\ell_{\infty}$
-ball of side length 1).
$\ell_{\infty}$
-ball of side length 1).
Remark. When
![]() $a_1,\dots,a_n$
and u belong to
$a_1,\dots,a_n$
and u belong to
![]() $\mathbb{Z}^{d}$
, as will be the case in our applications, the event ‘
$\mathbb{Z}^{d}$
, as will be the case in our applications, the event ‘
![]() $\|\sum_{i=1}^{n}\epsilon_i a_i - u \|_{\infty} < 1/2$
’ is equivalent to the event ‘
$\|\sum_{i=1}^{n}\epsilon_i a_i - u \|_{\infty} < 1/2$
’ is equivalent to the event ‘
![]() $\sum_{i=1}^{n}\epsilon_i a_i = u$
’. In this case, it was noted by Tao and Vu (Exercise 7.2.3 in [Reference Tao and VuTV06]) that the condition
$\sum_{i=1}^{n}\epsilon_i a_i = u$
’. In this case, it was noted by Tao and Vu (Exercise 7.2.3 in [Reference Tao and VuTV06]) that the condition
![]() $|\langle a_{i_j},e \rangle| \geq 1/(2\sqrt{d})$
may be relaxed to
$|\langle a_{i_j},e \rangle| \geq 1/(2\sqrt{d})$
may be relaxed to
![]() $|\langle a_{i_j},e \rangle| > 0$
. However, as stated, their proof still gives a constant
$|\langle a_{i_j},e \rangle| > 0$
. However, as stated, their proof still gives a constant
![]() $C(d) = \Theta(d)^d$
due to a ‘duplication’ step, which we will show is unnecessary.
$C(d) = \Theta(d)^d$
due to a ‘duplication’ step, which we will show is unnecessary.
There are two drawbacks to using the results mentioned above for the kinds of applications we have in mind. First, a constant of the form
![]() $C(d) = \Theta(d)^{d}$
does not give any non-trivial information when
$C(d) = \Theta(d)^{d}$
does not give any non-trivial information when
![]() $d = \omega(\sqrt{n})$
, whereas as discussed in the proof outline, we require an improvement over the Odlyzko bound for
$d = \omega(\sqrt{n})$
, whereas as discussed in the proof outline, we require an improvement over the Odlyzko bound for
![]() $d=\Theta(n)$
. Second, the hypotheses of these theorems, which involve two quantifiers (‘for all’ followed by ‘there exists’), are quite stringent and not easy to verify; in fact, we were unable to find any direct applications of Theorem 1.7 in the literature.
$d=\Theta(n)$
. Second, the hypotheses of these theorems, which involve two quantifiers (‘for all’ followed by ‘there exists’), are quite stringent and not easy to verify; in fact, we were unable to find any direct applications of Theorem 1.7 in the literature.
Our key structural observation is that a ‘pseudorandom’ rectangular matrix contains many disjoint submatrices of large rank. This motivates replacing the double quantifier hypothesis by a (weaker) hypothesis involving just one existential quantifier which, as we will see, is readily verified to hold in pseudorandom situations. Moreover, while our hypothesis is weaker, we are able to obtain conclusions with asymptotically much better constants, since our structural setting allows us to efficiently leverage the existing rich literature on anti-concentration of sums of independent random variables and anti-concentration of linear images of high dimensional distributions. In particular, we are able to give short and transparent proofs of our inequalities for very general classes of distributions; in contrast, Theorems 1.7 and 1.9 hold only for (vector)-weighted sums of independent Rademacher variables, and their proofs involve explicit trigonometric manipulations. We discuss this in more detail in Sections 2.2 and 3.1
Our first inequality is a strengthening of Theorem 1.9 in the setting of Section 1.2, both in terms of the hypothesis and the conclusion. A more general statement appears in Theorem 3.1.
Theorem 1.10. Let
![]() $a_{1},\dots,a_{n}$
be a collection vectors in
$a_{1},\dots,a_{n}$
be a collection vectors in
![]() $\mathbb{R}^{d}$
which can be partitioned as
$\mathbb{R}^{d}$
which can be partitioned as
![]() $\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
with
$\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
with
![]() $\ell$
even such that
$\ell$
even such that
![]() $\dim_{\mathbb{R}^d}(span\{a\,:\,a\in\mathcal{A}_{i}\})\,=\!:\,r_{i}$
. Then,
$\dim_{\mathbb{R}^d}(span\{a\,:\,a\in\mathcal{A}_{i}\})\,=\!:\,r_{i}$
. Then,
 \begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\sum_{i=1}^{n}\epsilon_{i}a_{i}=u\right]\leq\left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{\frac{r_{1}+\dots+r_{\ell}}{\ell}}\leq \left(\sqrt{\frac{2}{\pi\ell}}\left(1+O\left(\frac{1}{\ell}\right)\right)\right)^{\frac{r_{1}+\dots+r_{\ell}}{\ell}}.\end{equation*}
\begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\sum_{i=1}^{n}\epsilon_{i}a_{i}=u\right]\leq\left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{\frac{r_{1}+\dots+r_{\ell}}{\ell}}\leq \left(\sqrt{\frac{2}{\pi\ell}}\left(1+O\left(\frac{1}{\ell}\right)\right)\right)^{\frac{r_{1}+\dots+r_{\ell}}{\ell}}.\end{equation*}
Remark. This inequality is tight, as can be easily seen by taking (assuming n is divisible by d)
![]() $a_{i}$
to be
$a_{i}$
to be
![]() $e_{i\mod d}$
, where
$e_{i\mod d}$
, where
![]() $e_{1},\dots,e_{d}$
denotes the standard basis of
$e_{1},\dots,e_{d}$
denotes the standard basis of
![]() $\mathbb{R}^{d}$
, in which case we can take
$\mathbb{R}^{d}$
, in which case we can take
![]() $\ell = n/d$
and
$\ell = n/d$
and
![]() $r_1 = \dots = r_\ell = d$
.
$r_1 = \dots = r_\ell = d$
.
To see how Theorem 1.10 strengthens Theorem 1.9, note that the assumptions of Theorem 1.9 guarantee that there exist
![]() $\ell\,:\!=\, \lfloor m/d \rfloor$
disjoint subsets
$\ell\,:\!=\, \lfloor m/d \rfloor$
disjoint subsets
![]() $\mathcal{A}_1,\dots,\mathcal{A}_\ell$
such that
$\mathcal{A}_1,\dots,\mathcal{A}_\ell$
such that
![]() $r_1 = \dots = r_\ell = d$
. Such a collection of disjoint subsets can be obtained greedily by repeating the following construction
$r_1 = \dots = r_\ell = d$
. Such a collection of disjoint subsets can be obtained greedily by repeating the following construction
![]() $\ell$
times: let
$\ell$
times: let
![]() $v_1\in \{a_1,\dots,a_n\}$
be any nonzero vector that has not already been chosen in a previous iteration. Having chosen
$v_1\in \{a_1,\dots,a_n\}$
be any nonzero vector that has not already been chosen in a previous iteration. Having chosen
![]() $v_1,\dots,v_s$
for
$v_1,\dots,v_s$
for
![]() $s < d$
, let
$s < d$
, let
![]() $u_s \in (span\{v_1,\dots,v_s\})^\perp$
, and let
$u_s \in (span\{v_1,\dots,v_s\})^\perp$
, and let
![]() $v_{s+1}$
be any vector satisfying
$v_{s+1}$
be any vector satisfying
![]() $|\langle v_{s+1},u_{s}\rangle | > 0$
which has not already been chosen in a previous iteration – such a vector is guaranteed to exist since there are at least m choices of
$|\langle v_{s+1},u_{s}\rangle | > 0$
which has not already been chosen in a previous iteration – such a vector is guaranteed to exist since there are at least m choices of
![]() $v_{s+1}$
by assumption, of which at most
$v_{s+1}$
by assumption, of which at most
![]() $(\ell-1)d < m$
could have been chosen in a previous iteration. It follows that under the assumptions of Theorem 1.9, when
$(\ell-1)d < m$
could have been chosen in a previous iteration. It follows that under the assumptions of Theorem 1.9, when
![]() $a_1,\dots,a_n \in \mathbb{Z}^{d}$
, we have:
$a_1,\dots,a_n \in \mathbb{Z}^{d}$
, we have:
 \begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{\infty}<\frac{1}{2}\right]\leq C'(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
\begin{equation*}\sup_{u\in\mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_{i}a_{i}-u\right\|_{\infty}<\frac{1}{2}\right]\leq C'(d)\left(\frac{1}{\sqrt{m}}\right)^{d},\end{equation*}
where
![]() $C'(d) \leq \left(\sqrt{\frac{2d}{3}}\right)^{d}$
. In particular, we now have a non-trivial bound all the way up to
$C'(d) \leq \left(\sqrt{\frac{2d}{3}}\right)^{d}$
. In particular, we now have a non-trivial bound all the way up to
![]() $d=\Theta(m)$
, as opposed to just
$d=\Theta(m)$
, as opposed to just
![]() $d = O(\sqrt{m})$
as before.
$d = O(\sqrt{m})$
as before.
Although Theorem 1.10 is sufficient for the applications considered in this paper, we also provide a ‘small-ball probability’ version which may be useful in other contexts. In order to state it, we need the following definition.
Definition 1.11. The stable rank of A, denoted by
![]() $r_{s}(A)$
, is defined as
$r_{s}(A)$
, is defined as
 \begin{equation*}r_{s}(A)\,:\!=\,\left\lfloor\frac{\|A\|_{\text{HS}}^{2}}{\|A\|^{2}}\right\rfloor,\end{equation*}
\begin{equation*}r_{s}(A)\,:\!=\,\left\lfloor\frac{\|A\|_{\text{HS}}^{2}}{\|A\|^{2}}\right\rfloor,\end{equation*}
where
![]() $\|A\|_{\text{HS}}$
denotes the Hilbert–Schmidt norm of A, and
$\|A\|_{\text{HS}}$
denotes the Hilbert–Schmidt norm of A, and
![]() $\|A\|$
denotes the operator norm of A.
$\|A\|$
denotes the operator norm of A.
Remark. Recall that
![]() $\|A\| = s_1(A)$
and
$\|A\| = s_1(A)$
and
![]() $\|A\|_{\text{HS}}^{2} = \sum_{i=1}^{\text{rank}(A)} s_i(A)^2$
, where
$\|A\|_{\text{HS}}^{2} = \sum_{i=1}^{\text{rank}(A)} s_i(A)^2$
, where
![]() $s_1(A),s_2(A),\dots$
denote the singular values of A arranged in non-increasing order. Hence,
$s_1(A),s_2(A),\dots$
denote the singular values of A arranged in non-increasing order. Hence,
 \begin{equation*}r_s(A)\,:\!=\,\left\lfloor\frac{\sum_{i=1}^{\text{rank}(A)}s_i(A)^{2}}{s_1(A)^{2}}\right\rfloor;\end{equation*}
\begin{equation*}r_s(A)\,:\!=\,\left\lfloor\frac{\sum_{i=1}^{\text{rank}(A)}s_i(A)^{2}}{s_1(A)^{2}}\right\rfloor;\end{equation*}
in particular, for any non-zero matrix A,
![]() $1\leq r_s(A) \leq \text{rank}(A)$
, with the right inequality being an equality if and only if A is an orthogonal projection up to an isometry.
$1\leq r_s(A) \leq \text{rank}(A)$
, with the right inequality being an equality if and only if A is an orthogonal projection up to an isometry.
We can now state our inequality, which is proved by combining our general framework with a result of Rudelson and Vershynin [Reference Rudelson and VershyninRV14]. A more general version appears in Theorem 3.2.
Theorem 1.12. Let
![]() $a_{1},\dots,a_{n}$
be a collection vectors in
$a_{1},\dots,a_{n}$
be a collection vectors in
![]() $\mathbb{R}^{d}$
. For some
$\mathbb{R}^{d}$
. For some
![]() $\ell \in 2\mathbb{N}$
, let
$\ell \in 2\mathbb{N}$
, let
![]() $\mathcal{A}_1,\dots, \mathcal{A}_\ell$
be a partition of the set
$\mathcal{A}_1,\dots, \mathcal{A}_\ell$
be a partition of the set
![]() $\{a_1,\dots, a_n\}$
, and for each
$\{a_1,\dots, a_n\}$
, and for each
![]() $i \in [\ell]$
, let
$i \in [\ell]$
, let
![]() $A_i$
denote the
$A_i$
denote the
![]() $d\times |\mathcal{A}_i|$
dimensional matrix whose columns are given by the elements of
$d\times |\mathcal{A}_i|$
dimensional matrix whose columns are given by the elements of
![]() $\mathcal{A}_i$
. Then, for every
$\mathcal{A}_i$
. Then, for every
![]() $M \geq \max_{i\in [\ell]}\|A_i\|_{\text{HS}}$
and
$M \geq \max_{i\in [\ell]}\|A_i\|_{\text{HS}}$
and
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
 \begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_ia_i-u\right\|_{2}\leq M\right] \leq 2^{d}\prod_{i=1}^{\ell}\left(\frac{CM}{\sqrt{\varepsilon \ell}\|A_{i}\|_{\text{HS}}}\right)^{\frac{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}{\ell}},\end{equation*}
\begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\left\|\sum_{i=1}^{n}\epsilon_ia_i-u\right\|_{2}\leq M\right] \leq 2^{d}\prod_{i=1}^{\ell}\left(\frac{CM}{\sqrt{\varepsilon \ell}\|A_{i}\|_{\text{HS}}}\right)^{\frac{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}{\ell}},\end{equation*}
where
![]() $r_s(A_i)$
denotes the stable rank of
$r_s(A_i)$
denotes the stable rank of
![]() $A_i$
and C is an absolute constant.
$A_i$
and C is an absolute constant.
1.3. Counting
 $\{\pm1\}$
-valued normal matrices
$\{\pm1\}$
-valued normal matrices
Recall that a matrix M is normal if it commutes with its adjoint, i.e.,
![]() $MM^*=M^*M$
(for real matrices this is the same as
$MM^*=M^*M$
(for real matrices this is the same as
![]() $MM^T=M^TM$
). Recently, Deneanu and Vu [Reference Deneanu and VuDV19] studied the number of
$MM^T=M^TM$
). Recently, Deneanu and Vu [Reference Deneanu and VuDV19] studied the number of
![]() $n\times n$
$n\times n$
![]() $\{\pm1\}$
-valued normal matrices. Since real symmetric matrices are normal, there are at least
$\{\pm1\}$
-valued normal matrices. Since real symmetric matrices are normal, there are at least
![]() $2^{\binom{n+1}{2}}$
$2^{\binom{n+1}{2}}$
![]() $\{\pm 1\}$
-valued normal matrices. They conjectured that this lower bound is essentially sharp.
$\{\pm 1\}$
-valued normal matrices. They conjectured that this lower bound is essentially sharp.
Conjecture 1.13 (Deneanu-Vu, [Reference Deneanu and VuDV19]). There are
![]() $2^{(0.5+o(1))n^{2}}$
$2^{(0.5+o(1))n^{2}}$
![]() $n\times n$
$n\times n$
![]() $\{\pm 1\}$
-valued normal matrices.
$\{\pm 1\}$
-valued normal matrices.
As a first non-trivial step towards this conjecture, they showed the following.
Theorem 1.14 (Deneanu-Vu, [Reference Deneanu and VuDV19]). The number of
![]() $n\times n$
$n\times n$
![]() $\{\pm 1\}$
-valued normal matrices is at most
$\{\pm 1\}$
-valued normal matrices is at most
![]() $2^{(c_{DV}+o(1))n^{2}}$
for some constant
$2^{(c_{DV}+o(1))n^{2}}$
for some constant
![]() $c_{DV} < 0.698$
.
$c_{DV} < 0.698$
.
The problem of counting normal matrices also boils down to the problem of counting the number of solutions to some underdetermined system of linear equations, and using our framework, it is very easy to obtain an upper bound on the number of such matrices of the form
![]() $2^{(1-\alpha)n^2}$
, for some
$2^{(1-\alpha)n^2}$
, for some
![]() $\alpha > 0$
. Unfortunately, it does not seem that one can get
$\alpha > 0$
. Unfortunately, it does not seem that one can get
![]() $1-\alpha< c_{DV}$
using this simple method. However, the proof of Theorem 1.14 in [Reference Deneanu and VuDV19] itself uses the Odlyzko bound at a certain stage; therefore, by using their strategy as a black-box, with the application of the Odlyzko bound at this stage replaced by our better bound, we obtain:
$1-\alpha< c_{DV}$
using this simple method. However, the proof of Theorem 1.14 in [Reference Deneanu and VuDV19] itself uses the Odlyzko bound at a certain stage; therefore, by using their strategy as a black-box, with the application of the Odlyzko bound at this stage replaced by our better bound, we obtain:
Theorem 1.15. There exists some
![]() $\delta > 0$
such that the number of
$\delta > 0$
such that the number of
![]() $n\times n$
$n\times n$
![]() $\{\pm 1\}$
-valued normal matrices is at most
$\{\pm 1\}$
-valued normal matrices is at most
![]() $2^{(c_{DV}-\delta+o(1))n^{2}}$
, where
$2^{(c_{DV}-\delta+o(1))n^{2}}$
, where
![]() $c_{DV}$
denotes the constant in [Reference Deneanu and VuDV19].
$c_{DV}$
denotes the constant in [Reference Deneanu and VuDV19].
2. Tools
2.1. The Fourier transform
For
![]() $p\in [1,\infty)$
, let
$p\in [1,\infty)$
, let
![]() $\mathcal{L}^p(\mathbb{R}^d)$
denote the set of functions
$\mathcal{L}^p(\mathbb{R}^d)$
denote the set of functions
![]() $f\colon \mathbb{R}^d \to \mathbb{C}$
such that
$f\colon \mathbb{R}^d \to \mathbb{C}$
such that
![]() $\int_{\mathbb{R}^{d}}|f(x)|^{p}dx < \infty$
. For
$\int_{\mathbb{R}^{d}}|f(x)|^{p}dx < \infty$
. For
![]() $f\in \mathcal{L}^1(\mathbb{R}^d)$
, the Fourier transform of f – denoted by
$f\in \mathcal{L}^1(\mathbb{R}^d)$
, the Fourier transform of f – denoted by
![]() $\widehat{f}$
– is a function from
$\widehat{f}$
– is a function from
![]() $\mathbb{R}^{d}$
to
$\mathbb{R}^{d}$
to
![]() $\mathbb{C}$
given by
$\mathbb{C}$
given by
where
![]() $\langle x,\xi\rangle\,:\!=\,x_{1}\xi_{1}+\dots+x_{d}\xi_{d}$
denotes the standard inner product on
$\langle x,\xi\rangle\,:\!=\,x_{1}\xi_{1}+\dots+x_{d}\xi_{d}$
denotes the standard inner product on
![]() $\mathbb{R}^{d}$
. The convolution of
$\mathbb{R}^{d}$
. The convolution of
![]() $f,g \in \mathcal{L}^1(\mathbb{R}^d)$
, denoted by
$f,g \in \mathcal{L}^1(\mathbb{R}^d)$
, denoted by
![]() $f\ast g$
, is defined by
$f\ast g$
, is defined by
![]() $f\ast g(x) = \int_{\mathbb{R}^d}f(x-y)g(y)dy$
. Recall that for
$f\ast g(x) = \int_{\mathbb{R}^d}f(x-y)g(y)dy$
. Recall that for
![]() $f \in \mathcal{L}^1(\mathbb{R}^d)$
, the autocorrelation of f is defined by
$f \in \mathcal{L}^1(\mathbb{R}^d)$
, the autocorrelation of f is defined by
![]() $h(x) = \int_{\mathbb{R}^d}f(y)f(x+y)dy$
and satisfies
$h(x) = \int_{\mathbb{R}^d}f(y)f(x+y)dy$
and satisfies
![]() $\widehat{h}(\xi) = |\widehat{f}(\xi)|^2$
for all
$\widehat{h}(\xi) = |\widehat{f}(\xi)|^2$
for all
![]() $\xi \in \mathbb{R}^d$
.
$\xi \in \mathbb{R}^d$
.
The notion of Fourier transform extends more generally to finite Borel measures on
![]() $\mathbb{R}^d$
. For such a measure
$\mathbb{R}^d$
. For such a measure
![]() $\mu$
, the Fourier transform is a function from
$\mu$
, the Fourier transform is a function from
![]() $\mathbb{R}^{d}$
to
$\mathbb{R}^{d}$
to
![]() $\mathbb{C}$
given by
$\mathbb{C}$
given by
To see the connection with the Fourier transform for functions in
![]() $\mathcal{L}^1(\mathbb{R}^d)$
, note that if the measure
$\mathcal{L}^1(\mathbb{R}^d)$
, note that if the measure
![]() $\mu$
is absolutely continuous with respect to the Lebesgue measure
$\mu$
is absolutely continuous with respect to the Lebesgue measure
![]() $\lambda$
, then the density (more precisely, the Radon–Nikodym derivative)
$\lambda$
, then the density (more precisely, the Radon–Nikodym derivative)
![]() $f_\mu\,:\!=\, d\mu/d\lambda$
is in
$f_\mu\,:\!=\, d\mu/d\lambda$
is in
![]() $\mathcal{L}^1(\mathbb{R}^d)$
, and we have
$\mathcal{L}^1(\mathbb{R}^d)$
, and we have
![]() $\widehat{\mu}(\xi) = \widehat{f_\mu}(\xi)$
.
$\widehat{\mu}(\xi) = \widehat{f_\mu}(\xi)$
.
The only finite Borel measures we will deal with are those which arise as distributions of random vectors valued in
![]() $\mathbb{R}^d$
. For a d-dimensional random vector X, let
$\mathbb{R}^d$
. For a d-dimensional random vector X, let
![]() $\mu_X$
denote its distribution. Then, we have (see, e.g., [Reference DurrettDur10]):
$\mu_X$
denote its distribution. Then, we have (see, e.g., [Reference DurrettDur10]):
-
• (Inversion at atoms) Let X be a d-dimensional random vector. For any
 $x \in \mathbb{R}^d$
, where
$x \in \mathbb{R}^d$
, where \begin{equation*}\mu_{X}(\{x\}) = \lim_{T_1,\dots,T_d\to \infty}\frac{1}{\text{vol}(B[T_1,\dots,T_d])}\int_{B[T_1,\dots,T_d]}e^{2\pi i \langle x, t\rangle}\widehat{\mu_{X}}(t)dt,\end{equation*}
\begin{equation*}\mu_{X}(\{x\}) = \lim_{T_1,\dots,T_d\to \infty}\frac{1}{\text{vol}(B[T_1,\dots,T_d])}\int_{B[T_1,\dots,T_d]}e^{2\pi i \langle x, t\rangle}\widehat{\mu_{X}}(t)dt,\end{equation*}
 $B[T_1,\dots, T_d]$
denotes the box
$B[T_1,\dots, T_d]$
denotes the box
 $[-T_1,T_1]\times \dots \times [-T_d,T_d]$
.
$[-T_1,T_1]\times \dots \times [-T_d,T_d]$
.
-
• (Fourier transform of origin-symmetric random vectors) Let X be a d-dimensional, origin-symmetric random vector, i.e.
 $\mu_{X}(x) = \mu_{X}(-x)$
for all
$\mu_{X}(x) = \mu_{X}(-x)$
for all
 $x\in \mathbb{R}^d$
. Then,
$x\in \mathbb{R}^d$
. Then,
 $\widehat{\mu_X}$
is a real-valued function.
$\widehat{\mu_X}$
is a real-valued function.
2.2. Anti-concentration
Definition 2.1. For a random vector X valued in
![]() $\mathbb{R}^d$
, its (Euclidean) Lévy concentration function
$\mathbb{R}^d$
, its (Euclidean) Lévy concentration function
![]() $\mathcal{L}(X,\cdot)$
is a function from
$\mathcal{L}(X,\cdot)$
is a function from
![]() $\mathbb{R}^{\geq 0}$
to
$\mathbb{R}^{\geq 0}$
to
![]() $\mathbb{R}$
defined by
$\mathbb{R}$
defined by
Anti-concentration inequalities seek to upper bound the Lévy concentration function for various values of
![]() $\delta$
. In the discrete setting, a particularly important case is
$\delta$
. In the discrete setting, a particularly important case is
![]() $\delta=0$
, which corresponds to the size of the largest atom in the distribution of the random variable X. The proofs of our Halász-type inequalities will exploit two very general anti-concentration phenomena.
$\delta=0$
, which corresponds to the size of the largest atom in the distribution of the random variable X. The proofs of our Halász-type inequalities will exploit two very general anti-concentration phenomena.
The first principle states that sums of independent random variables do not concentrate much more than sums of suitable independent Gaussians. In particular, for the weighted sum of independent Rademacher variables, Erdös gave a beautiful combinatorial proof to show (improving on a previous bound of Littlewood and Offord) the following.
Theorem 2.2 (Erdõs, [Reference ErdösErd45]). Let
![]() $a=(a_{1},\dots,a_{n})$
be a vector in
$a=(a_{1},\dots,a_{n})$
be a vector in
![]() $\mathbb{R}^{n}$
all of whose entries are nonzero. Let
$\mathbb{R}^{n}$
all of whose entries are nonzero. Let
![]() $S_{a}$
denote the random sum
$S_{a}$
denote the random sum
![]() $\epsilon_{1}a_{1}+\dots+\epsilon_{n}a_{n}$
, where the
$\epsilon_{1}a_{1}+\dots+\epsilon_{n}a_{n}$
, where the
![]() $\epsilon_{i}$
’s are independent Rademacher random variables. Then,
$\epsilon_{i}$
’s are independent Rademacher random variables. Then,
 \begin{equation*}\sup_{c\in\mathbb{R}}\mathbb{P}[S_{a}=c]\leq\frac{{\bigg(\begin{array}{c}n\\[-3pt] \lfloor n/2\rfloor\end{array}\bigg)}}{2^{n}} \sim \sqrt{\frac{2}{\pi n}}.\end{equation*}
\begin{equation*}\sup_{c\in\mathbb{R}}\mathbb{P}[S_{a}=c]\leq\frac{{\bigg(\begin{array}{c}n\\[-3pt] \lfloor n/2\rfloor\end{array}\bigg)}}{2^{n}} \sim \sqrt{\frac{2}{\pi n}}.\end{equation*}
Up to a constant, this was subsequently generalised by Rogozin to handle the Lévy concentration function of sums of general independent random variables.
Theorem 2.3 (Rogozin, [Reference RogozinRog61]). There exists a universal constant
![]() $C>0$
such that for any independent random variables
$C>0$
such that for any independent random variables
![]() $X_{1},\dots,X_{n}$
, and any
$X_{1},\dots,X_{n}$
, and any
![]() $r>0$
, we have
$r>0$
, we have
 \begin{equation*}\mathcal{L}({S_n},\delta)\leq\frac{C}{\sqrt{\sum_{i=1}^{n}\left(1-\mathcal{L}({X_{i}},\delta)\right)}},\end{equation*}
\begin{equation*}\mathcal{L}({S_n},\delta)\leq\frac{C}{\sqrt{\sum_{i=1}^{n}\left(1-\mathcal{L}({X_{i}},\delta)\right)}},\end{equation*}
where
![]() $S_n\,:\!=\, X_1+\dots +X_n$
.
$S_n\,:\!=\, X_1+\dots +X_n$
.
The second anti-concentration principle concerns random vectors of the form AX, where A is a fixed
![]() $m\times n$
matrix, and
$m\times n$
matrix, and
![]() $X=(X_1,\dots,X_n)$
is a random vector with independent coordinates. It states roughly that if the
$X=(X_1,\dots,X_n)$
is a random vector with independent coordinates. It states roughly that if the
![]() $X_i$
’s are anti-concentrated on the line, and if A has large rank in a suitable sense, then the random vector AX is anti-concentrated in space [Reference Rudelson and VershyninRV14].
$X_i$
’s are anti-concentrated on the line, and if A has large rank in a suitable sense, then the random vector AX is anti-concentrated in space [Reference Rudelson and VershyninRV14].
As a first illustration of this principle, we present the following lemma, which may be viewed as a ‘tensorization’ of the Erdös-Littlewood-Offord inequality.
Lemma 2.4. Let A be an
![]() $m\times n$
matrix (where
$m\times n$
matrix (where
![]() $m\leq n$
) of rank r, and let X be a random vector distributed uniformly on
$m\leq n$
) of rank r, and let X be a random vector distributed uniformly on
![]() $\{\pm1\}^{n}$
. Then for any
$\{\pm1\}^{n}$
. Then for any
![]() $\ell\in\mathbb{N}$
,
$\ell\in\mathbb{N}$
,
 \begin{equation*}\sup_{u\in \mathbb{R}^{m}}\mathbb{P}[AX^{(1)}+\dots+AX^{(\ell)}=u]\leq\left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \lfloor \ell/2\rfloor\end{array}\bigg)}\right)^{r},\end{equation*}
\begin{equation*}\sup_{u\in \mathbb{R}^{m}}\mathbb{P}[AX^{(1)}+\dots+AX^{(\ell)}=u]\leq\left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \lfloor \ell/2\rfloor\end{array}\bigg)}\right)^{r},\end{equation*}
where
![]() $X^{(1)},\dots,X^{(\ell)}$
are i.i.d. copies of X.
$X^{(1)},\dots,X^{(\ell)}$
are i.i.d. copies of X.
Proof. By relabelling the coordinates if needed, we may write A as a block matrix
 $\left(\begin{array}{c@{\quad}c}E & F\\G & H\end{array}\right)$
where E is an
$\left(\begin{array}{c@{\quad}c}E & F\\G & H\end{array}\right)$
where E is an
![]() $r\times r$
invertible matrix, F is an
$r\times r$
invertible matrix, F is an
![]() $r\times(n-r)$
matrix, G is a
$r\times(n-r)$
matrix, G is a
![]() $(m-r)\times r$
matrix, and H is a
$(m-r)\times r$
matrix, and H is a
![]() $(m-r)\times(n-r)$
matrix. Let B denote the invertible
$(m-r)\times(n-r)$
matrix. Let B denote the invertible
![]() $m\times m$
matrix
$m\times m$
matrix
 $\left(\begin{array}{c@{\quad}c}E^{-1} & 0\\0 & I_{m-r}\end{array}\right)$
and note that
$\left(\begin{array}{c@{\quad}c}E^{-1} & 0\\0 & I_{m-r}\end{array}\right)$
and note that
 $BA=\left(\begin{array}{c@{\quad}c}I_{r} & \ast\\\ast & \ast\end{array}\right)$
. For a vector
$BA=\left(\begin{array}{c@{\quad}c}I_{r} & \ast\\\ast & \ast\end{array}\right)$
. For a vector
![]() $v\in\mathbb{R}^{s}$
with
$v\in\mathbb{R}^{s}$
with
![]() $s\geq r$
, let
$s\geq r$
, let
![]() $Q_{r}(v)\in\mathbb{R}^{r}$
denote the vector consisting of the first r coordinates of v. Also, let
$Q_{r}(v)\in\mathbb{R}^{r}$
denote the vector consisting of the first r coordinates of v. Also, let
![]() $X_{i}^{(j)}$
denote the ith coordinate of the random vector
$X_{i}^{(j)}$
denote the ith coordinate of the random vector
![]() $X^{(j)}$
, let
$X^{(j)}$
, let
![]() $\mathcal{R}$
denote the collection of random variables
$\mathcal{R}$
denote the collection of random variables
![]() $\{X_{r+1}^{(1)},\dots,X_{n}^{(1)},\dots, X_{r+1}^{(\ell)},\dots,X_{n}^{(\ell)}\}$
and let
$\{X_{r+1}^{(1)},\dots,X_{n}^{(1)},\dots, X_{r+1}^{(\ell)},\dots,X_{n}^{(\ell)}\}$
and let
![]() $\mathcal{S}$
denote the collection of random variables
$\mathcal{S}$
denote the collection of random variables
![]() $\{X^{(1)}_{1},\dots,X^{(1)}_{r},\dots,X^{(\ell)}_{1},\dots,X^{(\ell)}_{r}\}$
. Then for any
$\{X^{(1)}_{1},\dots,X^{(1)}_{r},\dots,X^{(\ell)}_{1},\dots,X^{(\ell)}_{r}\}$
. Then for any
![]() $u \in \mathbb{R}^m$
, we have:
$u \in \mathbb{R}^m$
, we have:
 \begin{eqnarray*}\mathbb{P}\left[AX^{(1)}+\dots+AX^{(\ell)}=u\right] & = & \mathbb{P}\left[BAX^{(1)}+\dots+BAX^{(\ell)}=Bu\right]\\ & \leq & \mathbb{P}\left[Q_{r}(BAX^{(1)})+\dots+Q_{r}(BAX^{(\ell)})=Q_{r}(Bu)\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\mathbb{P}_{\mathcal{S}}\left[Q_{r}(BAX^{(1)})+\dots+Q_{r}(BAX^{(\ell)})=Q_r(Bu)|\mathcal{R}\right]\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\mathbb{P}_{\mathcal{S}}\left[Q_{r}(X^{(1)})+\dots+Q_{r}(X^{(\ell)})=f(\mathcal{R})|\mathcal{R}\right]\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\prod_{i=1}^{r}\mathbb{P}_{\mathcal{S}}\left[X_{i}^{(1)}+\dots+X_{i}^{(\ell)}=f_{i}(\mathcal{R})|\mathcal{R}\right]\right]\\ & \leq & \mathbb{E}_{\mathcal{R}}\left[\prod_{i=1}^{r}2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right]\\ & = & \left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{r},\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[AX^{(1)}+\dots+AX^{(\ell)}=u\right] & = & \mathbb{P}\left[BAX^{(1)}+\dots+BAX^{(\ell)}=Bu\right]\\ & \leq & \mathbb{P}\left[Q_{r}(BAX^{(1)})+\dots+Q_{r}(BAX^{(\ell)})=Q_{r}(Bu)\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\mathbb{P}_{\mathcal{S}}\left[Q_{r}(BAX^{(1)})+\dots+Q_{r}(BAX^{(\ell)})=Q_r(Bu)|\mathcal{R}\right]\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\mathbb{P}_{\mathcal{S}}\left[Q_{r}(X^{(1)})+\dots+Q_{r}(X^{(\ell)})=f(\mathcal{R})|\mathcal{R}\right]\right]\\ & = & \mathbb{E}_{\mathcal{R}}\left[\prod_{i=1}^{r}\mathbb{P}_{\mathcal{S}}\left[X_{i}^{(1)}+\dots+X_{i}^{(\ell)}=f_{i}(\mathcal{R})|\mathcal{R}\right]\right]\\ & \leq & \mathbb{E}_{\mathcal{R}}\left[\prod_{i=1}^{r}2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right]\\ & = & \left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{r},\end{eqnarray*}
where the third line follows from the law of total probability; the fourth line follows from the explicit form of BA mentioned above; the fifth line follows from the independence of the coordinates of
![]() $X^{(j)}$
; and the sixth line follows from the Erdös–Littlewood–Offord inequality (Theorem 2.2). Taking the supremum over
$X^{(j)}$
; and the sixth line follows from the Erdös–Littlewood–Offord inequality (Theorem 2.2). Taking the supremum over
![]() $u \in \mathbb{R}^{m}$
completes the proof.
$u \in \mathbb{R}^{m}$
completes the proof.
Remark. By using Rogozin’s inequality (Theorem 2.3) instead of the Erdös–Littlewood–Offord inequality, we may generalize the lemma to handle any random vector
![]() $X=(X_1,\dots,X_n)$
with independent coordinates
$X=(X_1,\dots,X_n)$
with independent coordinates
![]() $X_i$
, provided we replace the conclusion by
$X_i$
, provided we replace the conclusion by
 \begin{equation*}\sup_{u\in \mathbb{R}^{m}}\mathbb{P}[AX^{(1)}+\dots+AX^{(\ell)}=u]\leq \left(\frac{C}{\ell}\right)^{r/2}\times \max_{I\subseteq[n], |I|=r}\prod_{i\in I}\frac{1}{\sqrt{1-\mathcal{L}({X_i},0)}},\end{equation*}
\begin{equation*}\sup_{u\in \mathbb{R}^{m}}\mathbb{P}[AX^{(1)}+\dots+AX^{(\ell)}=u]\leq \left(\frac{C}{\ell}\right)^{r/2}\times \max_{I\subseteq[n], |I|=r}\prod_{i\in I}\frac{1}{\sqrt{1-\mathcal{L}({X_i},0)}},\end{equation*}
where C is a universal constant.
For the Lévy concentration function for general
![]() $\delta$
, a version of Lemma 2.4 was proved by Rudelson and Vershynin in [Reference Rudelson and VershyninRV14].
$\delta$
, a version of Lemma 2.4 was proved by Rudelson and Vershynin in [Reference Rudelson and VershyninRV14].
Theorem 2.5 (Rudelson-Vershynin, [Reference Rudelson and VershyninRV14]). Consider a random vector
![]() $X=(X_{1},\dots,X_{d})$
where
$X=(X_{1},\dots,X_{d})$
where
![]() $X_{i}$
are real-valued independent random variables. Let
$X_{i}$
are real-valued independent random variables. Let
![]() $\delta,\rho\geq0$
be such that for all
$\delta,\rho\geq0$
be such that for all
![]() $i\in[d]$
,
$i\in[d]$
,
Then, for every
![]() $m\times n$
matrix A, every
$m\times n$
matrix A, every
![]() $M\geq1$
and every
$M\geq1$
and every
![]() $\varepsilon\in(0,1)$
, we have
$\varepsilon\in(0,1)$
, we have
where
![]() $C_{\varepsilon}=C/\sqrt{\varepsilon}$
for some absolute constant
$C_{\varepsilon}=C/\sqrt{\varepsilon}$
for some absolute constant
![]() $C > 0$
.
$C > 0$
.
More general statements of a similar nature may be found in [Reference Rudelson and VershyninRV14].
2.3. The replication trick
In this section, we present the ‘replication trick’, which allows us to reduce considerations about anti-concentration of sums of independent random vectors to considerations about anti-concentration of sums of independent
![]() ${identically\ distributed}$
random vectors. This will be useful since the ‘correct’ analog of Rogozin’s inequality for general random vectors with independent coordinates is not available; to our knowledge, the best result in this direction is due to Esseen [Reference EsseenEss66], who proved an inequality of this form for such random vectors satisfying additional symmetry conditions, which will not be available in our applications. The statement/proof of the ‘atomic’ version of the replication trick (Proposition 2.6) is similar in spirit to Corollaries 7.12 and 7.13 in [Reference Tao and VuTV06] with an important difference: we have no need for the lossy ‘domination’ and ‘duplication’ steps in [Reference Tao and VuTV06]; instead, we ensure the non-negativity of the Fourier transform at various places by using the previously stated simple fact that the Fourier transform of the distribution of an origin-symmetric random vector is real valued and restricting ourselves to even powers thereof.
${identically\ distributed}$
random vectors. This will be useful since the ‘correct’ analog of Rogozin’s inequality for general random vectors with independent coordinates is not available; to our knowledge, the best result in this direction is due to Esseen [Reference EsseenEss66], who proved an inequality of this form for such random vectors satisfying additional symmetry conditions, which will not be available in our applications. The statement/proof of the ‘atomic’ version of the replication trick (Proposition 2.6) is similar in spirit to Corollaries 7.12 and 7.13 in [Reference Tao and VuTV06] with an important difference: we have no need for the lossy ‘domination’ and ‘duplication’ steps in [Reference Tao and VuTV06]; instead, we ensure the non-negativity of the Fourier transform at various places by using the previously stated simple fact that the Fourier transform of the distribution of an origin-symmetric random vector is real valued and restricting ourselves to even powers thereof.
Proposition 2.6. Let
![]() $X_{1},\dots,X_{n}$
be independent random vectors valued in
$X_{1},\dots,X_{n}$
be independent random vectors valued in
![]() $\mathbb{R}^{d}$
. For each
$\mathbb{R}^{d}$
. For each
![]() $i\in[n]$
, let
$i\in[n]$
, let
![]() $\tilde{X}_{i}\,:\!=\,X_{i}-X^{\prime}_{i}$
, where
$\tilde{X}_{i}\,:\!=\,X_{i}-X^{\prime}_{i}$
, where
![]() $X^{\prime}_{i}$
is an independent copy of
$X^{\prime}_{i}$
is an independent copy of
![]() $X_{i}$
. Let
$X_{i}$
. Let
![]() $S_{n}\,:\!=\,X_{1}+\dots+X_{n}$
, and for any
$S_{n}\,:\!=\,X_{1}+\dots+X_{n}$
, and for any
![]() $i\in[n]$
,
$i\in[n]$
,
![]() $m\in\mathbb{N}$
, let
$m\in\mathbb{N}$
, let
![]() $\tilde{S}_{i,m}\,:\!=\,\tilde{X}_{i}^{(1)}+\dots\tilde{X}_{i}^{(m)}$
, where
$\tilde{S}_{i,m}\,:\!=\,\tilde{X}_{i}^{(1)}+\dots\tilde{X}_{i}^{(m)}$
, where
![]() $\tilde{X}_{i}^{(1)},\dots,\tilde{X}_{i}^{(m)}$
are independent copies of
$\tilde{X}_{i}^{(1)},\dots,\tilde{X}_{i}^{(m)}$
are independent copies of
![]() $\tilde{X}_{i}$
. Then for any
$\tilde{X}_{i}$
. Then for any
![]() $v\in\mathbb{R}^{d}$
and for any
$v\in\mathbb{R}^{d}$
and for any
![]() $a_{1},\dots,a_{n}\in4\cdot\mathbb{N}$
such that
$a_{1},\dots,a_{n}\in4\cdot\mathbb{N}$
such that
![]() $a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, we have
$a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, we have
Here,
![]() $4\cdot \mathbb{N}$
denotes the subset of natural numbers given by
$4\cdot \mathbb{N}$
denotes the subset of natural numbers given by
![]() $\{4m \colon m \in \mathbb{N}\}$
.
$\{4m \colon m \in \mathbb{N}\}$
.
Proof. As before, we let
![]() $\mu_X$
denote the distribution of the d-dimensional random vector X. We have:
$\mu_X$
denote the distribution of the d-dimensional random vector X. We have:
 \begin{eqnarray*}\mu_{S_{n}}(v) & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}e^{2\pi i\langle t,v\rangle}\widehat{\mu_{S_{n}}}(t)dt\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}e^{2\pi i\langle t,v\rangle}\prod_{i=1}^{n}\widehat{\mu_{X_{i}}}(t)dt\\[3pt] & \leq & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\left|\widehat{\mu_{X_{i}}}(t)\right|^{a_{i}}dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\left(\widehat{\mu_{\tilde{X_{i}}}}(t)\right)^{\frac{a_{i}}{2}}dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\widehat{\mu_{\tilde{S}_{i,a_{i}/2}}}(t)dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \prod_{i=1}^{n}\left(\lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}\widehat{\mu_{\tilde{S}_{i,a_{i}/2}}}(t)dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \prod_{i=1}^{n}\left(\mu_{\tilde{S}_{i,a_{i}/2}}(0)\right)^{\frac{1}{a_{i}}},\end{eqnarray*}
\begin{eqnarray*}\mu_{S_{n}}(v) & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}e^{2\pi i\langle t,v\rangle}\widehat{\mu_{S_{n}}}(t)dt\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}e^{2\pi i\langle t,v\rangle}\prod_{i=1}^{n}\widehat{\mu_{X_{i}}}(t)dt\\[3pt] & \leq & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\left|\widehat{\mu_{X_{i}}}(t)\right|^{a_{i}}dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\left(\widehat{\mu_{\tilde{X_{i}}}}(t)\right)^{\frac{a_{i}}{2}}dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\prod_{i=1}^{n}\left(\int_{B[T_{1},\dots,T_{d}]}\widehat{\mu_{\tilde{S}_{i,a_{i}/2}}}(t)dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \prod_{i=1}^{n}\left(\lim_{T_{1},\dots,T_{d}\to\infty}\frac{1}{\text{vol}B[T_{1},\dots,T_{d}]}\int_{B[T_{1},\dots,T_{d}]}\widehat{\mu_{\tilde{S}_{i,a_{i}/2}}}(t)dt\right)^{\frac{1}{a_{i}}}\\[3pt] & = & \prod_{i=1}^{n}\left(\mu_{\tilde{S}_{i,a_{i}/2}}(0)\right)^{\frac{1}{a_{i}}},\end{eqnarray*}
where the first line follows from the Fourier inversion formula at atoms; the second line follows from the independence of
![]() $X_1,\dots,X_n$
; the third line follows from Hölder’s inequality; the fourth line follows from the fact that
$X_1,\dots,X_n$
; the third line follows from Hölder’s inequality; the fourth line follows from the fact that
![]() $\widehat{\mu_{\tilde{X}_i}}(t) = |\widehat{\mu_{X_i}}(t)|^{2}$
(since the distribution of
$\widehat{\mu_{\tilde{X}_i}}(t) = |\widehat{\mu_{X_i}}(t)|^{2}$
(since the distribution of
![]() $\tilde{X_i}$
is the autocorrelation of the distribution of
$\tilde{X_i}$
is the autocorrelation of the distribution of
![]() $X_i$
); the fifth line follows from the independence of
$X_i$
); the fifth line follows from the independence of
![]() $\tilde{X}_i^{(1)}\dots,\tilde{X}_i^{(a_i/2)}$
; and the last line follows again from the Fourier inversion formula at atoms.
$\tilde{X}_i^{(1)}\dots,\tilde{X}_i^{(a_i/2)}$
; and the last line follows again from the Fourier inversion formula at atoms.
Remark. The same proof shows that when
![]() $X_{1},\dots,X_{n}$
are independent origin symmetric random vectors, then for any
$X_{1},\dots,X_{n}$
are independent origin symmetric random vectors, then for any
![]() $v\in\mathbb{R}^{d}$
$v\in\mathbb{R}^{d}$
for any
![]() $a_{1},\dots,a_{n}\in2\cdot\mathbb{N}$
such that
$a_{1},\dots,a_{n}\in2\cdot\mathbb{N}$
such that
![]() $a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, where
$a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, where
![]() $S_{i,a_i}$
denotes the sum of
$S_{i,a_i}$
denotes the sum of
![]() $a_i$
independent copies of
$a_i$
independent copies of
![]() $X_i$
.
$X_i$
.
The next proposition is a version of Proposition 2.6 for the Lévy concentration function. Essentially the same proof can also be used to prove variants for norms other than the Euclidean norm.
Proposition 2.7. Let
![]() $X_{1},\dots,X_{n}$
be independent random vectors valued in
$X_{1},\dots,X_{n}$
be independent random vectors valued in
![]() $\mathbb{R}^{d}$
. For each
$\mathbb{R}^{d}$
. For each
![]() $i\in[n]$
, let
$i\in[n]$
, let
![]() $\tilde{X}_{i}\,:\!=\,X_{i}-X^{\prime}_{i}$
, where
$\tilde{X}_{i}\,:\!=\,X_{i}-X^{\prime}_{i}$
, where
![]() $X^{\prime}_{i}$
is an independent copy of
$X^{\prime}_{i}$
is an independent copy of
![]() $X_{i}$
. Let
$X_{i}$
. Let
![]() $S_{n}\,:\!=\,X_{1}+\dots+X_{n}$
, and for any
$S_{n}\,:\!=\,X_{1}+\dots+X_{n}$
, and for any
![]() $i\in[n]$
,
$i\in[n]$
,
![]() $m\in\mathbb{N}$
, let
$m\in\mathbb{N}$
, let
![]() $\tilde{S}_{i,m}\,:\!=\,\tilde{X}_{i}^{(1)}+\dots\tilde{X}_{i}^{(m)}$
, where
$\tilde{S}_{i,m}\,:\!=\,\tilde{X}_{i}^{(1)}+\dots\tilde{X}_{i}^{(m)}$
, where
![]() $\tilde{X}_{i}^{(1)},\dots,\tilde{X}_{i}^{(m)}$
are independent copies of
$\tilde{X}_{i}^{(1)},\dots,\tilde{X}_{i}^{(m)}$
are independent copies of
![]() $\tilde{X}_{i}$
. Then for any
$\tilde{X}_{i}$
. Then for any
![]() $\delta > 0$
and for any
$\delta > 0$
and for any
![]() $a_{1},\dots,a_{n}\in4\cdot \mathbb{N}$
such that
$a_{1},\dots,a_{n}\in4\cdot \mathbb{N}$
such that
![]() $a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, we have
$a_{1}^{-1}+\dots+a_{n}^{-1}=1$
, we have
Proof. Let
![]() $\textbf{1}_{B_{\delta}(0)}$
denote the indicator function of the ball of radius
$\textbf{1}_{B_{\delta}(0)}$
denote the indicator function of the ball of radius
![]() $\delta$
centred at the origin. We will make use of the readily verified elementary inequality
$\delta$
centred at the origin. We will make use of the readily verified elementary inequality
By adding to each
![]() $X_i$
an independent random vector with distribution given by a ‘bump function’ with arbitrarily small support around the origin, we may assume that the distributions of all the random vectors under consideration are absolutely continuous with respect to the Lebesgue measure on
$X_i$
an independent random vector with distribution given by a ‘bump function’ with arbitrarily small support around the origin, we may assume that the distributions of all the random vectors under consideration are absolutely continuous with respect to the Lebesgue measure on
![]() $\mathbb{R}^{d}$
, and thus have densities. For such a random vector Y, we will denote its density with respect to the d-dimensional Lebesgue measure by
$\mathbb{R}^{d}$
, and thus have densities. For such a random vector Y, we will denote its density with respect to the d-dimensional Lebesgue measure by
![]() $f_Y$
. Then, for any
$f_Y$
. Then, for any
![]() $v\in \mathbb{R}^d$
, we have:
$v\in \mathbb{R}^d$
, we have:
 \begin{eqnarray*}\mathbb{P}\left[\|S_{n}-v\|_{2}\leq \delta\right] & = & \int_{x\in\mathbb{R}^{d}}\textbf{1}_{B_{\delta}(0)}(x)f_{S_{n}}(x+v)dx\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\int_{x\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)(x)f_{S_{n}}(x+v)dx\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)^{\wedge}(\xi)\widehat{f_{S_{n}}}(\xi)d\xi\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\prod_{i=1}^{n}\widehat{f_{X_{i}}}(\xi)d\xi\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\prod_{i=1}^{n}\left(\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{\frac{2}{a_{i}}}\widehat{f_{X_{i}}}(\xi)\right)d\xi\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\left|\widehat{f_{X_{i}}}(\xi)\right|^{a_{i}}d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\left(\widehat{f_{\tilde{X}_{i}}}(\xi)\right)^{\frac{a_{i}}{2}}d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)^{\wedge}(\xi)\widehat{f_{\tilde{S}_{i,a_{i}/2}}}(\xi)d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{x\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)(x)f_{\tilde{S}_{i,a_{i/2}}}(x)dx\right)^{\frac{1}{a_{i}}}\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\text{vol}(B_{2\delta}(0))\prod_{i=1}^{n}\left(\int_{x\in\mathbb{R}^{d}}\textbf{1}_{B(4\delta)}(x)f_{\tilde{S}_{i,a_{i/2}}}(x)dx\right)^{\frac{1}{a_{i}}}\\[2pt] & = & 2^{d}\prod_{i=1}^{n}\left(\mathbb{P}\left[\|\tilde{S}_{i,a_{i/2}}\|_{2}\leq4\delta\right]\right)^{\frac{1}{a_{i}}},\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[\|S_{n}-v\|_{2}\leq \delta\right] & = & \int_{x\in\mathbb{R}^{d}}\textbf{1}_{B_{\delta}(0)}(x)f_{S_{n}}(x+v)dx\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\int_{x\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)(x)f_{S_{n}}(x+v)dx\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)^{\wedge}(\xi)\widehat{f_{S_{n}}}(\xi)d\xi\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\prod_{i=1}^{n}\widehat{f_{X_{i}}}(\xi)d\xi\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\int_{\xi\in\mathbb{R}^{d}}e^{2\pi i\langle\xi,v\rangle}\prod_{i=1}^{n}\left(\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{\frac{2}{a_{i}}}\widehat{f_{X_{i}}}(\xi)\right)d\xi\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\left|\widehat{f_{X_{i}}}(\xi)\right|^{a_{i}}d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\widehat{\textbf{1}_{B(2\delta)}}(\xi)\right)^{2}\left(\widehat{f_{\tilde{X}_{i}}}(\xi)\right)^{\frac{a_{i}}{2}}d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{\xi\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)^{\wedge}(\xi)\widehat{f_{\tilde{S}_{i,a_{i}/2}}}(\xi)d\xi\right)^{\frac{1}{a_{i}}}\\[2pt] & = & \text{vol}(B_{\delta}(0))^{-1}\prod_{i=1}^{n}\left(\int_{x\in\mathbb{R}^{d}}\left(\textbf{1}_{B(2\delta)}\ast\textbf{1}_{B(2\delta)}\right)(x)f_{\tilde{S}_{i,a_{i/2}}}(x)dx\right)^{\frac{1}{a_{i}}}\\[2pt] & \leq & \text{vol}(B_{\delta}(0))^{-1}\text{vol}(B_{2\delta}(0))\prod_{i=1}^{n}\left(\int_{x\in\mathbb{R}^{d}}\textbf{1}_{B(4\delta)}(x)f_{\tilde{S}_{i,a_{i/2}}}(x)dx\right)^{\frac{1}{a_{i}}}\\[2pt] & = & 2^{d}\prod_{i=1}^{n}\left(\mathbb{P}\left[\|\tilde{S}_{i,a_{i/2}}\|_{2}\leq4\delta\right]\right)^{\frac{1}{a_{i}}},\end{eqnarray*}
where the second line follows from (2.1); the third line follows from Parseval’s formula; the fourth line follows from the convolution formula and the independence of
![]() $X_1,\dots,X_n$
; the sixth line follows from Hölder’s inequality, along with the fact that
$X_1,\dots,X_n$
; the sixth line follows from Hölder’s inequality, along with the fact that
![]() $\widehat{\textbf{1}_{B(2\delta)}}(\xi)$
is real valued for all
$\widehat{\textbf{1}_{B(2\delta)}}(\xi)$
is real valued for all
![]() $\xi \in \mathbb{R}^{d}$
and the seventh line follows from the fact that
$\xi \in \mathbb{R}^{d}$
and the seventh line follows from the fact that
![]() $|\widehat{f_{X_i}}(\xi)|^{2} = \widehat{f_{\tilde{X}_i}}(\xi)$
for all
$|\widehat{f_{X_i}}(\xi)|^{2} = \widehat{f_{\tilde{X}_i}}(\xi)$
for all
![]() $\xi \in \mathbb{R}^{d}$
; the ninth line follows again from Parseval’s formula; and the tenth line follows from (2.1). Taking the supremum over all
$\xi \in \mathbb{R}^{d}$
; the ninth line follows again from Parseval’s formula; and the tenth line follows from (2.1). Taking the supremum over all
![]() $v\in \mathbb{R}^{d}$
gives the desired conclusion.
$v\in \mathbb{R}^{d}$
gives the desired conclusion.
Remark. As in Section 2.3, if
![]() $X_1,\dots,X_n$
are origin-symmetric, then the same conclusion holds with
$X_1,\dots,X_n$
are origin-symmetric, then the same conclusion holds with
![]() $\tilde{S}_{i,a_i/2}$
replaced by
$\tilde{S}_{i,a_i/2}$
replaced by
![]() $S_{i,a_i}$
, for any
$S_{i,a_i}$
, for any
![]() $a_1,\dots,a_n \in 2\cdot\mathbb{N}$
with
$a_1,\dots,a_n \in 2\cdot\mathbb{N}$
with
![]() $a_1^{-1}+\dots+a_n^{-1} = 1$
.
$a_1^{-1}+\dots+a_n^{-1} = 1$
.
3. Proofs
3.1. Proofs of Halász-type inequalities
By combining the tools from Sections 2.2 and 2.3, we can now prove our Halász-type inequalities. All of them follow the same general outline. We begin by proving Theorem 1.10.
Proof of Theorem 1.10. Let
![]() $\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
be the partition of
$\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
be the partition of
![]() $\{a_{1},\dots,a_{n}\}$
as in the statement of the theorem. For each
$\{a_{1},\dots,a_{n}\}$
as in the statement of the theorem. For each
![]() $i\in[\ell]$
, let
$i\in[\ell]$
, let
![]() $A_{i}$
denote
$A_{i}$
denote
![]() $d\times|\mathcal{A}_{i}|$
dimensional matrix whose columns are given by the elements of
$d\times|\mathcal{A}_{i}|$
dimensional matrix whose columns are given by the elements of
![]() $\mathcal{A}_{i}$
. With this notation, we can rewrite the random vector
$\mathcal{A}_{i}$
. With this notation, we can rewrite the random vector
![]() $\sum_{i=1}^{n}\epsilon_{i}a_{i}$
as
$\sum_{i=1}^{n}\epsilon_{i}a_{i}$
as
![]() $\sum_{j=1}^{\ell}A_{j}Y_{j}$
, where
$\sum_{j=1}^{\ell}A_{j}Y_{j}$
, where
![]() $Y_{j}$
is uniformly distributed on
$Y_{j}$
is uniformly distributed on
![]() $\{\pm1\}^{|\mathcal{A}_{j}|}$
and
$\{\pm1\}^{|\mathcal{A}_{j}|}$
and
![]() $Y_{1},\dots,Y_{\ell}$
are independent.
$Y_{1},\dots,Y_{\ell}$
are independent.
Since the random vectors
![]() $X_{1}\,:\!=\,A_{1}Y_{1},\dots,X_{\ell}\,:\!=\,A_{\ell}Y_{\ell}$
are origin-symmetric, and since
$X_{1}\,:\!=\,A_{1}Y_{1},\dots,X_{\ell}\,:\!=\,A_{\ell}Y_{\ell}$
are origin-symmetric, and since
![]() $\ell\in2\cdot \mathbb{N}$
, it follows from Proposition 2.6 and Section 2.3 that for any
$\ell\in2\cdot \mathbb{N}$
, it follows from Proposition 2.6 and Section 2.3 that for any
![]() $u\in\mathbb{R}^{d}$
,
$u\in\mathbb{R}^{d}$
,
 \begin{eqnarray*}\mathbb{P}\left[\sum_{i=1}^{n}\epsilon_{i}a_{i}=u\right] & = & \mathbb{P}\left[\sum_{j=1}^{\ell}X_{j}=u\right]\\[4pt] & \leq & \prod_{j=1}^{\ell}\mathbb{P}\left[X_{j}^{(1)}+\dots+X_{j}^{(\ell)}=0\right]^{\frac{1}{\ell}},\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[\sum_{i=1}^{n}\epsilon_{i}a_{i}=u\right] & = & \mathbb{P}\left[\sum_{j=1}^{\ell}X_{j}=u\right]\\[4pt] & \leq & \prod_{j=1}^{\ell}\mathbb{P}\left[X_{j}^{(1)}+\dots+X_{j}^{(\ell)}=0\right]^{\frac{1}{\ell}},\end{eqnarray*}
where
![]() $X_j^{(1)},\dots, X_j^{(\ell)}$
are i.i.d. copies of
$X_j^{(1)},\dots, X_j^{(\ell)}$
are i.i.d. copies of
![]() $X_j$
. Further, since
$X_j$
. Further, since
![]() $\text{rank}(A_{j})=r_{j}$
by assumption, it follows from Lemma 2.4 that
$\text{rank}(A_{j})=r_{j}$
by assumption, it follows from Lemma 2.4 that
 \begin{eqnarray*}\mathbb{P}\left[X_{j}^{(1)}+\dots+X_{j}^{(\ell)}=0\right] & = & \mathbb{P}\left[A_{j}Y_{j}^{(1)}+\dots+A_{j}Y_{j}^{(\ell)}=0\right]\\[4pt] & \leq & \left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{r_{j}}.\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[X_{j}^{(1)}+\dots+X_{j}^{(\ell)}=0\right] & = & \mathbb{P}\left[A_{j}Y_{j}^{(1)}+\dots+A_{j}Y_{j}^{(\ell)}=0\right]\\[4pt] & \leq & \left(2^{-\ell}{\bigg(\begin{array}{c}\ell\\[-3pt] \ell/2\end{array}\bigg)}\right)^{r_{j}}.\end{eqnarray*}
Substituting this bound in the previous inequality completes the proof.
By using Section 2.2 instead of Lemma 2.4, we can use the same proof to obtain the following more general statement.
Theorem 3.1. Let
![]() $a_{1},\dots,a_{n}$
be a collection vectors in
$a_{1},\dots,a_{n}$
be a collection vectors in
![]() $\mathbb{R}^{d}$
which can be partitioned as
$\mathbb{R}^{d}$
which can be partitioned as
![]() $\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
such that
$\mathcal{A}_{1},\dots,\mathcal{A}_{\ell}$
such that
![]() $\dim_{\mathbb{R}^d}(span\{a\,:\,a\in\mathcal{A}_{i}\})\,=\!:\,r_{i}$
. Let
$\dim_{\mathbb{R}^d}(span\{a\,:\,a\in\mathcal{A}_{i}\})\,=\!:\,r_{i}$
. Let
![]() $x_1,\dots,x_n$
be independent random variables, and for each
$x_1,\dots,x_n$
be independent random variables, and for each
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $\tilde{x}_i\,:\!=\, x_i - x^{\prime}_i$
, where
$\tilde{x}_i\,:\!=\, x_i - x^{\prime}_i$
, where
![]() $x^{\prime}_i$
is an independent copy of
$x^{\prime}_i$
is an independent copy of
![]() $x_i$
. Then,
$x_i$
. Then,
 \begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\sum_{i=1}^{n}x_{i}a_{i}=u\right]\leq 2^{d}\inf_{(b_1,\dots,b_\ell)\in \mathcal{B}}\left(\frac{C}{\ell\lambda}\right)^{\sum_{i=1}^{\ell}\frac{r_i}{2b_i}},\end{equation*}
\begin{equation*}\sup_{u\in \mathbb{R}^{d}}\mathbb{P}\left[\sum_{i=1}^{n}x_{i}a_{i}=u\right]\leq 2^{d}\inf_{(b_1,\dots,b_\ell)\in \mathcal{B}}\left(\frac{C}{\ell\lambda}\right)^{\sum_{i=1}^{\ell}\frac{r_i}{2b_i}},\end{equation*}
where
![]() $\lambda \,:\!=\, \min_{i\in [n]}(1-\mathcal{L}_{\tilde{x}_i}(0)) $
and
$\lambda \,:\!=\, \min_{i\in [n]}(1-\mathcal{L}_{\tilde{x}_i}(0)) $
and
![]() $\mathcal{B} = \{(b_1,\dots,b_\ell)\in (4\cdot\mathbb{N})^\ell \,:\, b_1^{-1}+\dots + b_\ell^{-1} = 1\}$
.
$\mathcal{B} = \{(b_1,\dots,b_\ell)\in (4\cdot\mathbb{N})^\ell \,:\, b_1^{-1}+\dots + b_\ell^{-1} = 1\}$
.
We now state and prove the general small-ball version of our anti-concentration inequality.
Theorem 3.2. Let
![]() $a_{1},\dots,a_{n}$
be a collection vectors in
$a_{1},\dots,a_{n}$
be a collection vectors in
![]() $\mathbb{R}^{d}$
. Let
$\mathbb{R}^{d}$
. Let
![]() $\mathcal{A}_1,\dots, \mathcal{A}_\ell$
be a partition of the set
$\mathcal{A}_1,\dots, \mathcal{A}_\ell$
be a partition of the set
![]() $\{a_1,\dots, a_n\}$
, and for each
$\{a_1,\dots, a_n\}$
, and for each
![]() $i \in [\ell]$
, let
$i \in [\ell]$
, let
![]() $A_i$
denote the
$A_i$
denote the
![]() $d\times |\mathcal{A}_i|$
dimensional matrix whose columns are given by the elements of
$d\times |\mathcal{A}_i|$
dimensional matrix whose columns are given by the elements of
![]() $\mathcal{A}_i$
. Let
$\mathcal{A}_i$
. Let
![]() $x_1,\dots,x_n$
be independent random variables, and for each
$x_1,\dots,x_n$
be independent random variables, and for each
![]() $i\in [n]$
, let
$i\in [n]$
, let
![]() $\tilde{x}_i\,:\!=\, x_i - x^{\prime}_i$
, where
$\tilde{x}_i\,:\!=\, x_i - x^{\prime}_i$
, where
![]() $x^{\prime}_i$
is an independent copy of
$x^{\prime}_i$
is an independent copy of
![]() $x_i$
. Let
$x_i$
. Let
![]() $\delta,\lambda \geq 0$
be such that
$\delta,\lambda \geq 0$
be such that
![]() $\min_{i\in[n]}(1-\mathcal{L}(\tilde{x}_i,\delta)) = \lambda$
. Then, for every
$\min_{i\in[n]}(1-\mathcal{L}(\tilde{x}_i,\delta)) = \lambda$
. Then, for every
![]() $M \geq \max_{i \in [\ell]}\|A_{i}\|_{\text{HS}}$
and
$M \geq \max_{i \in [\ell]}\|A_{i}\|_{\text{HS}}$
and
![]() $\varepsilon \in (0,1)$
,
$\varepsilon \in (0,1)$
,
 \begin{equation*}\mathcal{L}\left(\sum_{i=1}^{n}x_ia_i, M\delta\right) \leq \inf_{(b_1,\dots,b_\ell)\in\mathcal{B}}\prod_{i=1}^{\ell}\left(\frac{CM}{\sqrt{\varepsilon b_i\lambda}\|A_{i}\|_{\text{HS}}}\right)^{\frac{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}{b_i}},\end{equation*}
\begin{equation*}\mathcal{L}\left(\sum_{i=1}^{n}x_ia_i, M\delta\right) \leq \inf_{(b_1,\dots,b_\ell)\in\mathcal{B}}\prod_{i=1}^{\ell}\left(\frac{CM}{\sqrt{\varepsilon b_i\lambda}\|A_{i}\|_{\text{HS}}}\right)^{\frac{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}{b_i}},\end{equation*}
where
![]() $r_s(A_i)$
denotes the stable rank of
$r_s(A_i)$
denotes the stable rank of
![]() $A_i$
, C is an absolute constant, and
$A_i$
, C is an absolute constant, and
![]() $\mathcal{B} = \{(b_1,\dots,b_\ell)\in (4\cdot\mathbb{N})^\ell \,:\, b_1^{-1}+\dots + b_\ell^{-1} = 1\}$
.
$\mathcal{B} = \{(b_1,\dots,b_\ell)\in (4\cdot\mathbb{N})^\ell \,:\, b_1^{-1}+\dots + b_\ell^{-1} = 1\}$
.
Proof. As before, we begin by rewriting the random vector
![]() $\sum_{i=1}^{n}x_{i}a_{i}$
as
$\sum_{i=1}^{n}x_{i}a_{i}$
as
![]() $\sum_{i=1}^{\ell}A_{i}Y_{i}$
. From Proposition 2.7, it follows that for any
$\sum_{i=1}^{\ell}A_{i}Y_{i}$
. From Proposition 2.7, it follows that for any
![]() $(b_{1},\dots,b_{\ell})\in\mathcal{B}$
,
$(b_{1},\dots,b_{\ell})\in\mathcal{B}$
,
 \begin{eqnarray*}\mathcal{L}\left(\sum_{i=1}^{n}x_{i}a_{i},M\delta\right) & = & \mathcal{L}\left(\sum_{i=1}^{\ell}A_{i}Y_{i},M\delta\right)\\ & \leq & 2^{d}\prod_{i=1}^{\ell}\mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M\delta\right)^{\frac{1}{b_{i}}}.\end{eqnarray*}
\begin{eqnarray*}\mathcal{L}\left(\sum_{i=1}^{n}x_{i}a_{i},M\delta\right) & = & \mathcal{L}\left(\sum_{i=1}^{\ell}A_{i}Y_{i},M\delta\right)\\ & \leq & 2^{d}\prod_{i=1}^{\ell}\mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M\delta\right)^{\frac{1}{b_{i}}}.\end{eqnarray*}
Next, since
![]() $1-\mathcal{L}(\tilde{x}_{i},\delta)\geq\lambda$
for all
$1-\mathcal{L}(\tilde{x}_{i},\delta)\geq\lambda$
for all
![]() $i\in[n]$
, it follows from Theorem 2.3 that
$i\in[n]$
, it follows from Theorem 2.3 that
where C is an absolute constant. In particular, all of the (independent) coordinates of the random vector
![]() $\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}$
have
$\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}$
have
![]() $\delta$
-Lévy concentrqseation function bounded by
$\delta$
-Lévy concentrqseation function bounded by
![]() $C/\sqrt{b_i\lambda}$
. Since
$C/\sqrt{b_i\lambda}$
. Since
![]() $M \geq \max_{i \in [\ell]}\|A_{i}\|_{\text{HS}}$
, we may write
$M \geq \max_{i \in [\ell]}\|A_{i}\|_{\text{HS}}$
, we may write
![]() $M = M_i \|A_{i}\|_{\text{HS}}$
for some
$M = M_i \|A_{i}\|_{\text{HS}}$
for some
![]() $M_i \geq 1$
. Hence, it follows from Theorem 2.5 that
$M_i \geq 1$
. Hence, it follows from Theorem 2.5 that
 \begin{align*}\mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M\delta\right)&= \mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M_i\|A_i\|_{\text{HS}}\delta\right)\\&\leq \left(\frac{CM_i}{\sqrt{\varepsilon b_i\lambda}}\right)^{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}\\&=\left(\frac{CM}{\sqrt{\varepsilon b_i\lambda}\|A_{i}\|_{\text{HS}}}\right)^{\lceil(1-\varepsilon)r_{s}(A_i)\rceil},\end{align*}
\begin{align*}\mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M\delta\right)&= \mathcal{L}\left(A_{i}\left(\tilde{Y}_{i}^{(1)}+\dots+\tilde{Y}_{i}^{(b_{i}/2)}\right),4M_i\|A_i\|_{\text{HS}}\delta\right)\\&\leq \left(\frac{CM_i}{\sqrt{\varepsilon b_i\lambda}}\right)^{\lceil(1-\varepsilon)r_{s}(A_i)\rceil}\\&=\left(\frac{CM}{\sqrt{\varepsilon b_i\lambda}\|A_{i}\|_{\text{HS}}}\right)^{\lceil(1-\varepsilon)r_{s}(A_i)\rceil},\end{align*}
where C is an absolute constant. Substituting this in the first inequality completes the proof.
Remark. When the
![]() $x_i$
’s are origin symmetric random variables, we may use Section 2.3 instead of Proposition 2.7 to obtain a similar conclusion – with the infimum now over the larger set
$x_i$
’s are origin symmetric random variables, we may use Section 2.3 instead of Proposition 2.7 to obtain a similar conclusion – with the infimum now over the larger set
![]() $\mathcal{B}'=\{(b_1,\dots,b_\ell)\in (2\cdot\mathbb{N})^{\ell}\colon b_1^{-1}+\dots+b_\ell^{-1}=1\}$
– under the assumption that
$\mathcal{B}'=\{(b_1,\dots,b_\ell)\in (2\cdot\mathbb{N})^{\ell}\colon b_1^{-1}+\dots+b_\ell^{-1}=1\}$
– under the assumption that
![]() $\min_{i\in[n]}(1-\mathcal{L}(x_i,\delta))=\lambda$
. In particular, if
$\min_{i\in[n]}(1-\mathcal{L}(x_i,\delta))=\lambda$
. In particular, if
![]() $\ell$
is even, then taking
$\ell$
is even, then taking
![]() $b_1=\dots=b_\ell = \ell$
gives Theorem 1.12.
$b_1=\dots=b_\ell = \ell$
gives Theorem 1.12.
3.2. Proof of Theorem 1.2
As in Section 1.1.1, let
![]() $H_{k,n}$
denote a
$H_{k,n}$
denote a
![]() $k\times n$
matrix with all its entries in
$k\times n$
matrix with all its entries in
![]() $\{\pm 1\}$
and all of whose rows are orthogonal. For convenience of notation, we isolate the following notion.
$\{\pm 1\}$
and all of whose rows are orthogonal. For convenience of notation, we isolate the following notion.
Definition 3.3. For any
![]() $r,\ell \in \mathbb{N}$
, a matrix M is said to admit an
$r,\ell \in \mathbb{N}$
, a matrix M is said to admit an
![]() $(r,\ell)$
-rank partition if there exists a decomposition of the columns of M into
$(r,\ell)$
-rank partition if there exists a decomposition of the columns of M into
![]() $\ell$
disjoint subsets, each of which corresponds to a submatrix of rank at least r.
$\ell$
disjoint subsets, each of which corresponds to a submatrix of rank at least r.
Note that the existence of an
![]() $(r,\ell)$
-rank partition is a uniform version of the condition appearing in Theorem 1.10. The next proposition shows that any
$(r,\ell)$
-rank partition is a uniform version of the condition appearing in Theorem 1.10. The next proposition shows that any
![]() $H_{k,n}$
admits an
$H_{k,n}$
admits an
![]() $(r,\ell)$
-rank partition with r and
$(r,\ell)$
-rank partition with r and
![]() $\ell$
sufficiently large.
$\ell$
sufficiently large.
Proposition 3.4. Let
![]() $r,\ell \in \mathbb{N}$
such that
$r,\ell \in \mathbb{N}$
such that
![]() $2\leq \ell, r \leq k \leq n/2$
,
$2\leq \ell, r \leq k \leq n/2$
,
![]() $2k \leq r\ell$
, and
$2k \leq r\ell$
, and
![]() $(e^{2}\ell)^{k}<(n/r)^{k-r}$
. Then,
$(e^{2}\ell)^{k}<(n/r)^{k-r}$
. Then,
![]() $H_{k,n}$
admits an
$H_{k,n}$
admits an
![]() $(r,\ell)$
-rank partition.
$(r,\ell)$
-rank partition.
Proof. The proof proceeds in two steps – first, we show that
![]() $H_{k,n}$
contains many non-zero
$H_{k,n}$
contains many non-zero
![]() $k\times k$
minors, and second, we apply a simple greedy procedure to these non-zero minors to produce an
$k\times k$
minors, and second, we apply a simple greedy procedure to these non-zero minors to produce an
![]() $(r,\ell)$
-rank partition for the desired values of r and
$(r,\ell)$
-rank partition for the desired values of r and
![]() $\ell$
.
$\ell$
.
The first step follows easily from the classical Cauchy–Binet formula (see, e.g., [Reference Aigner, Ziegler, Hofmann and ErdosAZHE10]), which asserts that:
where
![]() $\mathcal{M}_k$
denotes the set of all
$\mathcal{M}_k$
denotes the set of all
![]() $k\times k$
submatrices of
$k\times k$
submatrices of
![]() $H_{k,n}$
. In our case,
$H_{k,n}$
. In our case,
![]() $H_{k,n}H_{k,n}^{T} = n\text{Id}_{k}$
, so that
$H_{k,n}H_{k,n}^{T} = n\text{Id}_{k}$
, so that
![]() $\det(H_{k,n}H_{k,n}^{T}) = n^{k}$
. Moreover, since each
$\det(H_{k,n}H_{k,n}^{T}) = n^{k}$
. Moreover, since each
![]() $A \in \mathcal{M}_k$
is a
$A \in \mathcal{M}_k$
is a
![]() $k\times k$
$k\times k$
![]() $\{\pm 1\}$
-valued matrix,
$\{\pm 1\}$
-valued matrix,
![]() $\det(A)^{2} \leq k^{k}$
(with equality attained if and only if A is itself a Hadamard matrix). Hence, it follows from the Cauchy–Binet formula that
$\det(A)^{2} \leq k^{k}$
(with equality attained if and only if A is itself a Hadamard matrix). Hence, it follows from the Cauchy–Binet formula that
![]() $H_{n,k}$
has at least
$H_{n,k}$
has at least
![]() $(n/k)^{k}$
non-zero minors.
$(n/k)^{k}$
non-zero minors.
Next, we use these non-zero minors to construct an
![]() $(r,\ell)$
-rank partition in
$(r,\ell)$
-rank partition in
![]() $\ell$
steps as follows: In Step 1, choose r columns of an arbitrary non-zero minor – such a minor is guaranteed to exist by the discussion above. Let
$\ell$
steps as follows: In Step 1, choose r columns of an arbitrary non-zero minor – such a minor is guaranteed to exist by the discussion above. Let
![]() $\mathcal{C}_K$
denote the union of the columns chosen by the end of Step K, for any
$\mathcal{C}_K$
denote the union of the columns chosen by the end of Step K, for any
![]() $1\leq K \leq \ell -1$
. In Step
$1\leq K \leq \ell -1$
. In Step
![]() $K+1$
, we choose r linearly independent columns which are disjoint from
$K+1$
, we choose r linearly independent columns which are disjoint from
![]() $\mathcal{C}_K$
. Then, the
$\mathcal{C}_K$
. Then, the
![]() $\ell$
collections of r columns chosen at different steps give an
$\ell$
collections of r columns chosen at different steps give an
![]() $(r,\ell)$
-rank partition of
$(r,\ell)$
-rank partition of
![]() $H_{k,n}$
.
$H_{k,n}$
.
Therefore, to complete the proof, it only remains to show that for each
![]() $1\leq K\leq \ell-1$
, there is a choice of r linearly independent columns which are disjoint from
$1\leq K\leq \ell-1$
, there is a choice of r linearly independent columns which are disjoint from
![]() $\mathcal{C}_K$
. Since
$\mathcal{C}_K$
. Since
![]() $|\mathcal{C}_K|=rK$
, this is in turn implied by the stronger statement that for any collection
$|\mathcal{C}_K|=rK$
, this is in turn implied by the stronger statement that for any collection
![]() $\mathcal{C}$
of at most
$\mathcal{C}$
of at most
![]() $r\ell$
columns, there is a choice of r linearly independent columns which are disjoint from
$r\ell$
columns, there is a choice of r linearly independent columns which are disjoint from
![]() $\mathcal{C}$
. In order to see this, we note that the number of
$\mathcal{C}$
. In order to see this, we note that the number of
![]() $k\times k$
submatrices of
$k\times k$
submatrices of
![]() $H_{k,n}$
which have at least
$H_{k,n}$
which have at least
![]() $k-r$
columns contained in
$k-r$
columns contained in
![]() $\mathcal{C}$
is at most:
$\mathcal{C}$
is at most:
 \begin{eqnarray*}\sum_{s=0}^{r}{\bigg(\begin{array}{c}r\ell\\[-3pt] k-s\end{array}\bigg)}{\bigg(\begin{array}{c}n\\[-3pt] s\end{array}\bigg)} & \leq & {\bigg(\begin{array}{c}r\ell\\[-3pt] k\end{array}\bigg)}\sum_{s=0}^{r}{\bigg(\begin{array}{c}n\\[-3pt] s\end{array}\bigg)}\\ & \leq & \left(\frac{er\ell}{k}\right)^{k}\left(\frac{en}{r}\right)^{r}\\ & < & \left(\frac{n}{k}\right)^{k},\end{eqnarray*}
\begin{eqnarray*}\sum_{s=0}^{r}{\bigg(\begin{array}{c}r\ell\\[-3pt] k-s\end{array}\bigg)}{\bigg(\begin{array}{c}n\\[-3pt] s\end{array}\bigg)} & \leq & {\bigg(\begin{array}{c}r\ell\\[-3pt] k\end{array}\bigg)}\sum_{s=0}^{r}{\bigg(\begin{array}{c}n\\[-3pt] s\end{array}\bigg)}\\ & \leq & \left(\frac{er\ell}{k}\right)^{k}\left(\frac{en}{r}\right)^{r}\\ & < & \left(\frac{n}{k}\right)^{k},\end{eqnarray*}
where the first inequality uses
![]() $2k\leq r\ell$
, the second inequality uses
$2k\leq r\ell$
, the second inequality uses
![]() $2r \leq n$
, and the final inequality follows by assumption. Since there are at least
$2r \leq n$
, and the final inequality follows by assumption. Since there are at least
![]() $(n/k)^{k}$
non-zero minors of
$(n/k)^{k}$
non-zero minors of
![]() $H_{k,n}$
, it follows that there exists a
$H_{k,n}$
, it follows that there exists a
![]() $k\times k$
submatrix
$k\times k$
submatrix
![]() $A_{K+1}$
of
$A_{K+1}$
of
![]() $H_{n,k}$
of full rank which shares at most
$H_{n,k}$
of full rank which shares at most
![]() $k-r$
columns with
$k-r$
columns with
![]() $\mathcal{C}_K$
. In particular,
$\mathcal{C}_K$
. In particular,
![]() $A_{K+1}$
contains r linearly independent columns which are disjoint from
$A_{K+1}$
contains r linearly independent columns which are disjoint from
![]() $\mathcal{C}_K$
, as desired.
$\mathcal{C}_K$
, as desired.
Given the discussion in Section 1.1.1, the previous proposition essentially completes the proof of Theorem 1.2.
Proof of Theorem 1.2. We claim that there exist absolute constants
![]() $0<c_1<c_2 <1/2$
such that for all n sufficiently large and
$0<c_1<c_2 <1/2$
such that for all n sufficiently large and
![]() $k\in [c_1n,c_2n]$
, the number of solutions
$k\in [c_1n,c_2n]$
, the number of solutions
![]() $x\in \{\pm 1\}^{n}$
to
$x\in \{\pm 1\}^{n}$
to
![]() $H_{k,n}x = 0$
is at most
$H_{k,n}x = 0$
is at most
![]() $2^{n-(3k/2)}$
. Indeed, for all
$2^{n-(3k/2)}$
. Indeed, for all
![]() $100\leq k \leq n/2000$
, it is easy to check that the assumptions of Proposition 3.4 are satisfied for
$100\leq k \leq n/2000$
, it is easy to check that the assumptions of Proposition 3.4 are satisfied for
![]() $r=\lfloor k/2\rfloor$
and
$r=\lfloor k/2\rfloor$
and
![]() $\ell = \lfloor\sqrt{n/ke^{4}}\rfloor \geq 5$
. Hence, it follows from Proposition 3.4 that for all
$\ell = \lfloor\sqrt{n/ke^{4}}\rfloor \geq 5$
. Hence, it follows from Proposition 3.4 that for all
![]() $100\leq k \leq n/2000$
,
$100\leq k \leq n/2000$
,
![]() $H_{k,n}$
admits an
$H_{k,n}$
admits an
![]() $(r,\ell)$
-rank partition with the specified values of r and
$(r,\ell)$
-rank partition with the specified values of r and
![]() $\ell$
.
$\ell$
.
Therefore, by Theorem 1.10, it follows that there exists an absolute constant
![]() $C > 0$
such that for all n sufficiently large and
$C > 0$
such that for all n sufficiently large and
![]() $100\leq k \leq n/(10000C)^2$
, the number of solutions
$100\leq k \leq n/(10000C)^2$
, the number of solutions
![]() $x\in \{\pm 1\}^{n}$
to
$x\in \{\pm 1\}^{n}$
to
![]() $H_{k,n}x = 0$
is at most
$H_{k,n}x = 0$
is at most
 \begin{align*} 2^{n}\cdot \left(\frac{C}{\ell}\right)^{r/2} &\leq 2^{n}\cdot \left(\frac{1}{1000}\right)^{k/5} \leq 2^{n}3^{-k}\\ &\leq 2^{n - (3/2)k},\end{align*}
\begin{align*} 2^{n}\cdot \left(\frac{C}{\ell}\right)^{r/2} &\leq 2^{n}\cdot \left(\frac{1}{1000}\right)^{k/5} \leq 2^{n}3^{-k}\\ &\leq 2^{n - (3/2)k},\end{align*}
which proves the claim with
![]() $c_2 = n/(10000C)^2$
and
$c_2 = n/(10000C)^2$
and
![]() $c_1 = c_2/2$
(say).
$c_1 = c_2/2$
(say).
Finally, given this claim, we have from (1.1) that for all n sufficiently large,
 \begin{align*} H(n) &\leq \prod_{i=0}^{n-1}2^{n-i}\prod_{k=c_1 n}^{c_2 n}2^{-k/2}\\ &\leq 2^{\binom{n+1}{2}}2^{-\frac{(c_2^2 - c_1^2)n^2}{4}}\\ &\leq 2^{\binom{n+1}{2}}2^{-\frac{c_2^2 n^2}{16}},\end{align*}
\begin{align*} H(n) &\leq \prod_{i=0}^{n-1}2^{n-i}\prod_{k=c_1 n}^{c_2 n}2^{-k/2}\\ &\leq 2^{\binom{n+1}{2}}2^{-\frac{(c_2^2 - c_1^2)n^2}{4}}\\ &\leq 2^{\binom{n+1}{2}}2^{-\frac{c_2^2 n^2}{16}},\end{align*}
which completes the proof.
Remark. For our problem of providing an upper bound on the number of Hadamard matrices, we could have used the somewhat simpler Proposition 3.6 (see below) instead of Proposition 3.4; this proposition shows that there are very few
![]() $H_{k,n}$
which do not admit an
$H_{k,n}$
which do not admit an
![]() $(r,\ell)$
-rank partition for sufficiently large
$(r,\ell)$
-rank partition for sufficiently large
![]() $r,\ell$
. However, we used Proposition 3.4 to show that it is easy to find such a rank partition even for a given
$r,\ell$
. However, we used Proposition 3.4 to show that it is easy to find such a rank partition even for a given
![]() $k\times n$
system of linear equations A – indeed, the proof of Proposition 3.4 goes through as long as
$k\times n$
system of linear equations A – indeed, the proof of Proposition 3.4 goes through as long as
![]() $\det(AA^T)$
is ‘large’ (which is indeed the case for random or ‘pseudorandom’ A), and all
$\det(AA^T)$
is ‘large’ (which is indeed the case for random or ‘pseudorandom’ A), and all
![]() $k\times k$
minors of A are uniformly bounded (which is guaranteed in settings where A has restricted entries, as in our case).
$k\times k$
minors of A are uniformly bounded (which is guaranteed in settings where A has restricted entries, as in our case).
3.3. Proof of Theorem 1.15
In this section, we show how to obtain a non-trivial upper bound on the number of
![]() $\{\pm 1\}$
-valued normal matrices using our general framework. As mentioned in the introduction, this bound by itself is not stronger than the one obtained by Deneanu and Vu [Reference Deneanu and VuDV19]; however, it can be used in their proof in a modular fashion to obtain an improvement over their bound, thereby proving Theorem 1.15. As the proof of Deneanu and Vu is quite technical, we defer the details of this second step to Appendix A.
$\{\pm 1\}$
-valued normal matrices using our general framework. As mentioned in the introduction, this bound by itself is not stronger than the one obtained by Deneanu and Vu [Reference Deneanu and VuDV19]; however, it can be used in their proof in a modular fashion to obtain an improvement over their bound, thereby proving Theorem 1.15. As the proof of Deneanu and Vu is quite technical, we defer the details of this second step to Appendix A.
Following Deneanu and Vu, we consider the following generalization of the notion of normality:
Definition 3.5. Let N be a fixed (but otherwise arbitrary)
![]() $n\times n$
matrix. An
$n\times n$
matrix. An
![]() $n\times n$
matrix M is said to be N-normal if and only if
$n\times n$
matrix M is said to be N-normal if and only if
For any
![]() $n\times n$
matrix N, we let
$n\times n$
matrix N, we let
![]() $\mathcal N(N)$
denote the set of all
$\mathcal N(N)$
denote the set of all
![]() $n\times n$
,
$n\times n$
,
![]() $\{\pm 1\}$
-valued matrices which are N-normal. In particular,
$\{\pm 1\}$
-valued matrices which are N-normal. In particular,
![]() $\mathcal{N}(0)$
is the set of all
$\mathcal{N}(0)$
is the set of all
![]() $n\times n$
,
$n\times n$
,
![]() $\{\pm 1\}$
-valued normal matrices. The notion of N-normality is crucial to the proof of Deneanu and Vu, which is based on an inductive argument – they show that the quantity
$\{\pm 1\}$
-valued normal matrices. The notion of N-normality is crucial to the proof of Deneanu and Vu, which is based on an inductive argument – they show that the quantity
![]() $2^{(c_{DV}+o(1))n^{2}}$
in Theorem 1.14 is actually a uniform upper bound on the size of the set
$2^{(c_{DV}+o(1))n^{2}}$
in Theorem 1.14 is actually a uniform upper bound on the size of the set
![]() $\mathcal{N}(N)$
for any N. While this general notion of normality is not required to obtain some non-trivial upper bound on the number of normal matrices, either using our framework or theirs, we will state and prove the results of this section for N-normality, since this greater generality will be essential in Appendix A.
$\mathcal{N}(N)$
for any N. While this general notion of normality is not required to obtain some non-trivial upper bound on the number of normal matrices, either using our framework or theirs, we will state and prove the results of this section for N-normality, since this greater generality will be essential in Appendix A.
We begin by introducing some notation and discussing how to profitably recast the problem of counting N-normal matrices as a problem of counting the number of solutions to an underdetermined system of linear equations. Given any matrix X, we let
![]() $r_i(X)$
and
$r_i(X)$
and
![]() $c_i(X)$
denote its
$c_i(X)$
denote its
![]() $i^{th}$
row and column, respectively. With this notation, note that for a given matrix M, being N-normal is equivalent to satisfying the following equation for all
$i^{th}$
row and column, respectively. With this notation, note that for a given matrix M, being N-normal is equivalent to satisfying the following equation for all
![]() $i,j \in [n]$
:
$i,j \in [n]$
:
In particular, writing M in block form as
 \begin{equation*}M=\left[\begin{array}{c@{\quad}c} A_k & B_k\\ C_k & D_k\end{array}\right],\end{equation*}
\begin{equation*}M=\left[\begin{array}{c@{\quad}c} A_k & B_k\\ C_k & D_k\end{array}\right],\end{equation*}
where
![]() $A_k$
is a
$A_k$
is a
![]() $k\times k$
matrix, we see that (3.1) amounts to the following equations:
$k\times k$
matrix, we see that (3.1) amounts to the following equations:
-
(i) For all
 $i,j\in[k]$
:
$i,j\in[k]$
:  \begin{equation*}r_i(A_k)r_j(A_k)^T+r_i(B_k)r_j(B_k)^T-c_i(A_k)^Tc_j(A_k)-c_i(C_k)^Tc_j(C_k)=N_{ij}.\end{equation*}
\begin{equation*}r_i(A_k)r_j(A_k)^T+r_i(B_k)r_j(B_k)^T-c_i(A_k)^Tc_j(A_k)-c_i(C_k)^Tc_j(C_k)=N_{ij}.\end{equation*}
-
(ii) For all
 $i\in[k],j\in[n-k]$
:
$i\in[k],j\in[n-k]$
:  \begin{equation*}r_i(A_k)r_j(C_k)^T+r_i(B_k)r_j(D_k)^T-c_i(A_k)^Tc_j(B_k)-c_i(C_k)^Tc_j(D_k)=N_{i,k+j}.\end{equation*}
\begin{equation*}r_i(A_k)r_j(C_k)^T+r_i(B_k)r_j(D_k)^T-c_i(A_k)^Tc_j(B_k)-c_i(C_k)^Tc_j(D_k)=N_{i,k+j}.\end{equation*}
-
(iii) For all
 $i,j\in[n-k]$
:
$i,j\in[n-k]$
:  \begin{equation*}r_i(C_k)r_j(C_k)^T+r_i(D_k)r_j(D_k)^T-c_i(B_k)^Tc_j(B_k)-c_i(D_k)^Tc_j(D_k)=N_{k+i,k+j}.\end{equation*}
\begin{equation*}r_i(C_k)r_j(C_k)^T+r_i(D_k)r_j(D_k)^T-c_i(B_k)^Tc_j(B_k)-c_i(D_k)^Tc_j(D_k)=N_{k+i,k+j}.\end{equation*}
We now rewrite this system of equations in a form that will be useful for our application. Following Deneanu and Vu, we will count the size of
![]() $\mathcal{N}(N)$
by constructing N-normal matrices in
$\mathcal{N}(N)$
by constructing N-normal matrices in
![]() $n+1$
steps and bounding the number of choices available at each step. The steps are as follows: in Step 0, we select n entries
$n+1$
steps and bounding the number of choices available at each step. The steps are as follows: in Step 0, we select n entries
![]() $d_1,\dots, d_n$
to serve as diagonal entries of the matrix M; in Step k for
$d_1,\dots, d_n$
to serve as diagonal entries of the matrix M; in Step k for
![]() $1\leq k\leq n$
, we select
$1\leq k\leq n$
, we select
![]() $2(n-k)$
entries so as to completely determine the
$2(n-k)$
entries so as to completely determine the
![]() $k^{th}$
row and the
$k^{th}$
row and the
![]() $k^{th}$
column of M – of course, these
$k^{th}$
column of M – of course, these
![]() $2(n-k)$
entries cannot be chosen arbitrarily and must satisfy some constraints coming from the choice of entries in Steps
$2(n-k)$
entries cannot be chosen arbitrarily and must satisfy some constraints coming from the choice of entries in Steps
![]() $0,\dots,k-1$
.
$0,\dots,k-1$
.
More precisely, let
![]() $M_k$
denote the structure obtained at the end of Step k. Then,
$M_k$
denote the structure obtained at the end of Step k. Then,
 \begin{equation}M_k=\left[\begin{array}{c|c}A_k & B_k\\ \hline C_k & \begin{array}{c@{\quad}c@{\quad}c}d_{k+1} & * &*\\ *&\ddots&* \\ *&*&d_n \\ \end{array} \end{array}\right],\end{equation}
\begin{equation}M_k=\left[\begin{array}{c|c}A_k & B_k\\ \hline C_k & \begin{array}{c@{\quad}c@{\quad}c}d_{k+1} & * &*\\ *&\ddots&* \\ *&*&d_n \\ \end{array} \end{array}\right],\end{equation}
where the
![]() $*$
’s denote the parts of
$*$
’s denote the parts of
![]() $D_k$
which have not been determined by the end of Step k. Observe that the matrix
$D_k$
which have not been determined by the end of Step k. Observe that the matrix
![]() $A_k$
, together with the first column of
$A_k$
, together with the first column of
![]() $B_k$
, the first row of
$B_k$
, the first row of
![]() $C_k$
, and the diagonal element
$C_k$
, and the diagonal element
![]() $d_{k+1}$
forms the matrix
$d_{k+1}$
forms the matrix
![]() $A_{k+1}$
; in particular, the matrix
$A_{k+1}$
; in particular, the matrix
![]() $A_{k+1}$
is already determined at the end of Step k. Moreover, both
$A_{k+1}$
is already determined at the end of Step k. Moreover, both
![]() $B_{k+1}$
and
$B_{k+1}$
and
![]() $C_{k+1}$
are determined at the end of Step k up to their last row and last column, respectively.
$C_{k+1}$
are determined at the end of Step k up to their last row and last column, respectively.
In Step
![]() $k+1$
, we choose
$k+1$
, we choose
![]() $r_{k+1}(B_{k+1})$
and
$r_{k+1}(B_{k+1})$
and
![]() $c_{k+1}(C_{k+1})$
. In order to make this choice in a manner such that the resulting
$c_{k+1}(C_{k+1})$
. In order to make this choice in a manner such that the resulting
![]() $M_{k+1}$
admits even a single extension to an N-normal matrix, it is necessary that for all
$M_{k+1}$
admits even a single extension to an N-normal matrix, it is necessary that for all
![]() $i\in[k]$
:
$i\in[k]$
:
Since
![]() $A_{k+1}$
is completely determined by the end of Step k, and since N is fixed, we can rewrite the above equation as: for all
$A_{k+1}$
is completely determined by the end of Step k, and since N is fixed, we can rewrite the above equation as: for all
![]() $i\in [k]$
,
$i\in [k]$
,
for some
![]() $N^{\prime}_{k+1,i}$
which is uniquely determined at the end of Step k. Let
$N^{\prime}_{k+1,i}$
which is uniquely determined at the end of Step k. Let
![]() $N^{\prime}_{k}$
be the k-dimensional column vector whose
$N^{\prime}_{k}$
be the k-dimensional column vector whose
![]() $i^{th}$
entry is given by
$i^{th}$
entry is given by
![]() $N^{\prime}_{k+1,i}$
, let
$N^{\prime}_{k+1,i}$
, let
![]() $T_{k}\,:\!=\,[U\text{ } V]$
be the
$T_{k}\,:\!=\,[U\text{ } V]$
be the
![]() $k\times 2(n-k-1)$
matrix formed by taking U to be the matrix consisting of the first k rows of
$k\times 2(n-k-1)$
matrix formed by taking U to be the matrix consisting of the first k rows of
![]() $B_{k+1}$
and
$B_{k+1}$
and
![]() $V^{T}$
to be the matrix consisting of the first k columns of
$V^{T}$
to be the matrix consisting of the first k columns of
![]() $C_{k+1}$
, and let
$C_{k+1}$
, and let
![]() $x_k$
be the
$x_k$
be the
![]() $2(n-k-1)$
-dimensional column vector given by
$2(n-k-1)$
-dimensional column vector given by
 $x_k\,:\!=\,\left[\begin{array}{c} r_{k+1}^T(B_{k+1})\\-c_{k+1}(C_{k+1}) \end{array}\right]$
. With this notation, (3.3) can be written as
$x_k\,:\!=\,\left[\begin{array}{c} r_{k+1}^T(B_{k+1})\\-c_{k+1}(C_{k+1}) \end{array}\right]$
. With this notation, (3.3) can be written as
The next proposition is the analogue of Proposition 3.4 in the present setting.
Proposition 3.6. Let
![]() $0 < \gamma < 1$
be fixed, and let M be a random
$0 < \gamma < 1$
be fixed, and let M be a random
![]() $m\times n^{\prime}$
$m\times n^{\prime}$
![]() $\{\pm 1\}$
-valued random matrix with
$\{\pm 1\}$
-valued random matrix with
![]() $m\leq n'$
. Let
$m\leq n'$
. Let
![]() $\mathcal{E}_{\gamma,\ell}$
denote the event that M does not admit a
$\mathcal{E}_{\gamma,\ell}$
denote the event that M does not admit a
![]() $(\gamma m,\ell)$
-rank partition. Then,
$(\gamma m,\ell)$
-rank partition. Then,
The proof of this proposition is based on the following lemma, which follows easily from Odlyzko’s lemma (Lemma 1.4).
Lemma 3.7. Let
![]() $0 < \gamma < 1$
be fixed, and let M be a random
$0 < \gamma < 1$
be fixed, and let M be a random
![]() $m\times m$
$m\times m$
![]() $\{\pm 1\}$
-valued random matrix. Then,
$\{\pm 1\}$
-valued random matrix. Then,
Proof. For any integer
![]() $1\leq s\leq m$
, let
$1\leq s\leq m$
, let
![]() $\mathcal{R}_s$
denote the event that
$\mathcal{R}_s$
denote the event that
![]() $rank(M)=s$
. Since
$rank(M)=s$
. Since
 \begin{equation*}\mathbb{P}[rank(M)\leq \gamma m] = \mathbb{P}\left[\bigvee_{s=1}^{m}\mathcal{R}_{s}\right]\leq \sum_{s=1}^{\gamma m}\mathbb{P}[\mathcal{R}_s],\end{equation*}
\begin{equation*}\mathbb{P}[rank(M)\leq \gamma m] = \mathbb{P}\left[\bigvee_{s=1}^{m}\mathcal{R}_{s}\right]\leq \sum_{s=1}^{\gamma m}\mathbb{P}[\mathcal{R}_s],\end{equation*}
it suffices to show that
![]() $\mathbb{P}[\mathcal{R}_s]\leq 2^{-(1-\gamma)^{2}m^{2}+O(m)} $
for all
$\mathbb{P}[\mathcal{R}_s]\leq 2^{-(1-\gamma)^{2}m^{2}+O(m)} $
for all
![]() $s\in [\gamma m]$
. To see this, note by symmetry that
$s\in [\gamma m]$
. To see this, note by symmetry that
where
![]() $\mathcal{I}_{[s]}$
is the event that the first s rows of M are linearly independent. Moreover, letting
$\mathcal{I}_{[s]}$
is the event that the first s rows of M are linearly independent. Moreover, letting
![]() $r_{[s+1,n]}(M)$
denote the set
$r_{[s+1,n]}(M)$
denote the set
![]() $\{r_{s+1}(M),\dots,r_m(M)\}$
of the last
$\{r_{s+1}(M),\dots,r_m(M)\}$
of the last
![]() $m-s$
rows of M, and
$m-s$
rows of M, and
![]() $V_s$
denote the random vector space spanned by the first s rows of M, we have:
$V_s$
denote the random vector space spanned by the first s rows of M, we have:
 \begin{eqnarray*}\mathbb{P}\left[\mathcal{R}_{s}\wedge\mathcal{I}_{[s]}\right] & \leq & \mathbb{P}\left[r_{[s+1,n]}\subseteq V_s\right]\\ & = & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}\mathbb{P}\left[r_{[s+1,n]}(M)\subseteq V_s|r_{i}(M)=v_{i},1\leq i\leq s\right]\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & = & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}\left(\prod_{j=s+1}^{m}\mathbb{P}\left[r_{j}(M)\in V_s|r_{i}(M)=v_{i},1\leq i\leq s\right]\right)\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & \leq & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}2^{(s-m)(m-s)}\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & = & 2^{-(m-s)^{2}},\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[\mathcal{R}_{s}\wedge\mathcal{I}_{[s]}\right] & \leq & \mathbb{P}\left[r_{[s+1,n]}\subseteq V_s\right]\\ & = & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}\mathbb{P}\left[r_{[s+1,n]}(M)\subseteq V_s|r_{i}(M)=v_{i},1\leq i\leq s\right]\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & = & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}\left(\prod_{j=s+1}^{m}\mathbb{P}\left[r_{j}(M)\in V_s|r_{i}(M)=v_{i},1\leq i\leq s\right]\right)\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & \leq & \sum_{v_{1},\dots,v_{s}\in\{\pm1\}^{m}}2^{(s-m)(m-s)}\mathbb{P}\left[r_{i}(M)=v_{i},1\leq i\leq s\right]\\ & = & 2^{-(m-s)^{2}},\end{eqnarray*}
where the second line follows from the law of total probability; the third line follows from the independence of the rows of the matrix M; and the fourth line follows from Odlyzko’s lemma (Lemma 1.4) along with the fact that conditioning on the values of
![]() $r_1(M),\dots,r_s(M)$
fixes
$r_1(M),\dots,r_s(M)$
fixes
![]() $V_s$
to be a subspace of dimension at most s.
$V_s$
to be a subspace of dimension at most s.
Finally, since
![]() $m-s\geq (1-\gamma)m$
and
$m-s\geq (1-\gamma)m$
and
![]() ${\bigg(\begin{array}{c}m\\[-3pt] s\end{array}\bigg)} \leq 2^{m}$
, we get the desired conclusion.
${\bigg(\begin{array}{c}m\\[-3pt] s\end{array}\bigg)} \leq 2^{m}$
, we get the desired conclusion.
Proof of Proposition 3.6. We may assume without loss of generality that
![]() $\ell m < n'$
; otherwise, the desired upper bound on
$\ell m < n'$
; otherwise, the desired upper bound on
![]() $\mathbb{P}[\mathcal{E}_{\gamma, \ell}]$
is at least
$\mathbb{P}[\mathcal{E}_{\gamma, \ell}]$
is at least
![]() $2^{O(n')}$
, which trivially holds since
$2^{O(n')}$
, which trivially holds since
![]() $2^{O(n')} \geq 1$
.
$2^{O(n')} \geq 1$
.
For each
![]() $i\in [t]$
, where
$i\in [t]$
, where
![]() $t = \lfloor n'/m\rfloor$
, let
$t = \lfloor n'/m\rfloor$
, let
![]() $A_i$
denote the
$A_i$
denote the
![]() $m\times m$
submatrix of M consisting of the columns
$m\times m$
submatrix of M consisting of the columns
![]() $c_{(i-1)m+1}(M),\dots,c_{im}(M)$
. Then,
$c_{(i-1)m+1}(M),\dots,c_{im}(M)$
. Then,
By Lemma 3.7, we have for each
![]() $i\in [t]$
that
$i\in [t]$
that
Therefore, since the entries of the different
![]() $A_i$
’s are independent, the probability of having more than
$A_i$
’s are independent, the probability of having more than
![]() $t-\ell$
indices
$t-\ell$
indices
![]() $i\in [t]$
for which
$i\in [t]$
for which
![]() $\textrm{rank}(A_i)\leq \gamma m$
is at most:
$\textrm{rank}(A_i)\leq \gamma m$
is at most:
 \begin{align*}\sum_{k=t-\ell+1}^{t}{\bigg(\begin{array}{c}t\\[-3pt] k\end{array}\bigg)}\left(2^{-(1-\gamma)^{2}m^{2}+O(m)}\right)^{k} & \leq t2^{t}2^{-(1-\gamma)^{2}m^{2}(t-\ell)+O(tm)}\\ & \leq 2^{-(1-\gamma)^{2}m^{2}t+(1-\gamma)^{2}m^{2}\ell+O(tm)}\\ & \leq 2^{-(1-\gamma)^{2}mn'+(1-\gamma)^{2}(m^{2}\ell+m^{2})+O(n')},\end{align*}
\begin{align*}\sum_{k=t-\ell+1}^{t}{\bigg(\begin{array}{c}t\\[-3pt] k\end{array}\bigg)}\left(2^{-(1-\gamma)^{2}m^{2}+O(m)}\right)^{k} & \leq t2^{t}2^{-(1-\gamma)^{2}m^{2}(t-\ell)+O(tm)}\\ & \leq 2^{-(1-\gamma)^{2}m^{2}t+(1-\gamma)^{2}m^{2}\ell+O(tm)}\\ & \leq 2^{-(1-\gamma)^{2}mn'+(1-\gamma)^{2}(m^{2}\ell+m^{2})+O(n')},\end{align*}
which completes the proof.
We need one final piece of notation. For
![]() $1\leq k \leq n$
, we define the set of k-partial matrices – denoted by
$1\leq k \leq n$
, we define the set of k-partial matrices – denoted by
![]() $\mathcal{P}_{k}$
– to be
$\mathcal{P}_{k}$
– to be
![]() $\{\pm 1, \ast\}$
-valued matrices of the form (3.2) (i.e. we require these matrices to have
$\{\pm 1, \ast\}$
-valued matrices of the form (3.2) (i.e. we require these matrices to have
![]() $\ast$
’s in exactly the same positions as in (3.2)). For any
$\ast$
’s in exactly the same positions as in (3.2)). For any
![]() $n\times n$
$n\times n$
![]() $\{\pm1\}$
-valued matrix M, let
$\{\pm1\}$
-valued matrix M, let
![]() $M_k$
denote the k-partial matrix obtained from M. For any
$M_k$
denote the k-partial matrix obtained from M. For any
![]() $1\leq k \leq n$
and any
$1\leq k \leq n$
and any
![]() $n\times n$
matrix N, we define:
$n\times n$
matrix N, we define:
In words,
![]() $\mathcal{S}_k(N)$
denotes all the possible k-partial matrices arising from N-normal matrices. The following proposition is the main result of this section.
$\mathcal{S}_k(N)$
denotes all the possible k-partial matrices arising from N-normal matrices. The following proposition is the main result of this section.
Proposition 3.8. There exist absolute constants
![]() $\beta,\delta>0$
such that for any
$\beta,\delta>0$
such that for any
![]() $n\times n$
matrix N,
$n\times n$
matrix N,
Given this proposition, it is immediate to obtain a non-trivial upper bound on the number of
![]() $\{\pm 1\}$
-valued N-normal matrices. Indeed, any N-normal matrix must be an ‘extension’ of a matrix in
$\{\pm 1\}$
-valued N-normal matrices. Indeed, any N-normal matrix must be an ‘extension’ of a matrix in
![]() $\mathcal{S}_{\beta n}(N)$
; on the other hand, any matrix in
$\mathcal{S}_{\beta n}(N)$
; on the other hand, any matrix in
![]() $\mathcal{S}_{\beta n}(N)$
can be extended to at most
$\mathcal{S}_{\beta n}(N)$
can be extended to at most
![]() $2^{(1-\beta)^2n^2}$
N-normal matrices (as
$2^{(1-\beta)^2n^2}$
N-normal matrices (as
![]() $D_{\beta n}$
is an
$D_{\beta n}$
is an
![]() $n(1-\beta)\times n(1-\beta)$
$n(1-\beta)\times n(1-\beta)$
![]() $\{\pm 1\}$
-valued matrix). Hence, the number of N-normal matrices is at most
$\{\pm 1\}$
-valued matrix). Hence, the number of N-normal matrices is at most
![]() $2^{(2\beta-\beta^2)n^2-\delta n^2+(1-\beta)^2n^2}=2^{(1-\delta)n^2+o(n^2)}$
.
$2^{(2\beta-\beta^2)n^2-\delta n^2+(1-\beta)^2n^2}=2^{(1-\delta)n^2+o(n^2)}$
.
Proof. For any m-partial matrix P and for any
![]() $1\leq k \leq m$
, let
$1\leq k \leq m$
, let
![]() $T_k(P)$
denote the
$T_k(P)$
denote the
![]() $k \times 2(n-k-1)$
matrix obtained from P as in (3.4). We will estimate the size of
$k \times 2(n-k-1)$
matrix obtained from P as in (3.4). We will estimate the size of
![]() $\mathcal{S}_{\beta n}(N)$
by considering the following two cases.
$\mathcal{S}_{\beta n}(N)$
by considering the following two cases.
First, we bound the number of partial matrices P in
![]() $\mathcal{P}_{\beta n}$
such that for some
$\mathcal{P}_{\beta n}$
such that for some
![]() $\beta n/2 \leq k \leq \beta n$
,
$\beta n/2 \leq k \leq \beta n$
,
![]() $T_{k}(P)$
does not admit a
$T_{k}(P)$
does not admit a
![]() $(\gamma k,\ell_k)$
-rank-partition, where
$(\gamma k,\ell_k)$
-rank-partition, where
![]() $\ell_k=n'/2k, n'=2(n-k-1)$
, and
$\ell_k=n'/2k, n'=2(n-k-1)$
, and
![]() $0<\gamma <1$
is some constant to be chosen later. For this, note that Proposition 3.6 shows that there are at most
$0<\gamma <1$
is some constant to be chosen later. For this, note that Proposition 3.6 shows that there are at most
choices for such a
![]() $T_k(P)$
, provided
$T_k(P)$
, provided
![]() $k < n'/4$
, which holds for (say)
$k < n'/4$
, which holds for (say)
![]() $\beta < 1/4$
. Since the remaining unknown entries of P which are not in
$\beta < 1/4$
. Since the remaining unknown entries of P which are not in
![]() $T_{k}(P)$
are
$T_{k}(P)$
are
![]() $\{\pm 1\}$
-valued, this shows that the number of
$\{\pm 1\}$
-valued, this shows that the number of
![]() $\beta n$
partial matrices satisfying this first case is bounded above by
$\beta n$
partial matrices satisfying this first case is bounded above by
for all
![]() $\beta < 1/4$
.
$\beta < 1/4$
.
Second, we bound the number of partial matrices
![]() $P \in \mathcal{S}_{\beta n}(N)$
which have the additional property that
$P \in \mathcal{S}_{\beta n}(N)$
which have the additional property that
![]() $T_k(P)$
admits a
$T_k(P)$
admits a
![]() $(\gamma k, \ell_k)$
-rank-partition for all
$(\gamma k, \ell_k)$
-rank-partition for all
![]() $\beta n/2 \leq k \leq \beta n$
. In this case, Theorem 1.10 shows that for any
$\beta n/2 \leq k \leq \beta n$
. In this case, Theorem 1.10 shows that for any
![]() $\beta n/2 \leq k \leq \beta n$
, the number of
$\beta n/2 \leq k \leq \beta n$
, the number of
![]() $\{\pm 1\}$
-valued solutions to (3.4)
$\{\pm 1\}$
-valued solutions to (3.4)
![]() $T_k(P)x_k=N'$
is at most
$T_k(P)x_k=N'$
is at most
where in the last inequality, we have used
![]() $2(n-k-1)\geq n$
for all
$2(n-k-1)\geq n$
for all
![]() $k\leq \beta n$
, which is certainly true for
$k\leq \beta n$
, which is certainly true for
![]() $\beta < 1/4$
. In other words, for a fixed
$\beta < 1/4$
. In other words, for a fixed
![]() $T_k(P)$
, there are at most
$T_k(P)$
, there are at most
![]() $2^{2(n-k-1)-\frac{\gamma k}{2}\log_{2}\frac{n}{2k}}$
ways to extend it to
$2^{2(n-k-1)-\frac{\gamma k}{2}\log_{2}\frac{n}{2k}}$
ways to extend it to
![]() $T_{k+1}(P')$
for some
$T_{k+1}(P')$
for some
![]() $P'\in \mathcal{S}_{\beta n}(N)$
. Hence, it follows that the number of matrices in
$P'\in \mathcal{S}_{\beta n}(N)$
. Hence, it follows that the number of matrices in
![]() $\mathcal{S}_{\beta n}(N)$
with this additional property (stated at the beginning of the paragraph) is at most:
$\mathcal{S}_{\beta n}(N)$
with this additional property (stated at the beginning of the paragraph) is at most:
for
![]() $\beta < 1/4$
. Combining these two cases completes the proof.
$\beta < 1/4$
. Combining these two cases completes the proof.
Remark. In particular, if we take
![]() $\gamma = 3/4$
, it follows that for
$\gamma = 3/4$
, it follows that for
![]() $\beta$
sufficiently small (say
$\beta$
sufficiently small (say
![]() $\beta \leq 2^{-10}$
), we can take
$\beta \leq 2^{-10}$
), we can take
![]() $\delta \geq \beta^{2}$
.
$\delta \geq \beta^{2}$
.
In Appendix A, we will use Proposition 3.8 along with the strategy of [Reference Deneanu and VuDV19] to prove Theorem 1.15.
Acknowledgements
V.J. would like to thank Ethan Yale Jaffe for his insightful comments. A.F. and Y.Z. would like to thank Gwen McKinley, Guy Moshkovitz and Clara Shikhelman for helpful discussions at the initial stage of this project. The authors are grateful to an anonymous referee for their careful reading of the manuscript and for suggestions which have improved the presentation.
A.F. was partially supported by NSF DMS-6935855. V.J. was partially supported by NSF CCF 1665252 and DMS-1737944 and ONR N00014-17-1-2598. Y.Z. was partially supported by NSF DMS-1362326 and DMS-1764176.
The work was done when A.F. and V.J. were both at the Massachusetts Institute of Technology.
Appendix A. Completing the proof of Theorem 1.15
We now show how to combine the strategy of Deneanu and Vu with subsec-proof-normality in order to prove Theorem 1.15. We begin with a few definitions.
Definition A.1. Let
![]() $S_n$
denote the symmetric group on n letters. For any
$S_n$
denote the symmetric group on n letters. For any
![]() $\sigma\in S_n$
and for any
$\sigma\in S_n$
and for any
![]() $n\times n$
matrix M, we define
$n\times n$
matrix M, we define
where
![]() $P_{\sigma}$
is the permutation matrix representing
$P_{\sigma}$
is the permutation matrix representing
![]() $\sigma$
. In other words,
$\sigma$
. In other words,
![]() $M_{\sigma}$
is the matrix obtained from M by permuting the row and columns according to
$M_{\sigma}$
is the matrix obtained from M by permuting the row and columns according to
![]() $\sigma$
.
$\sigma$
.
The previous definition motivates the following equivalence relation
![]() $\sim$
on the set of
$\sim$
on the set of
![]() $n\times n$
matrices: given two
$n\times n$
matrices: given two
![]() $n\times n$
matrices M and M
′, we say that
$n\times n$
matrices M and M
′, we say that
![]() $M \sim M'$
if and only if there exists
$M \sim M'$
if and only if there exists
![]() $\sigma \in S_n$
such that
$\sigma \in S_n$
such that
![]() $M' = M_\sigma$
. The next definition isolates a notion of normality which is invariant under this equivalence relation.
$M' = M_\sigma$
. The next definition isolates a notion of normality which is invariant under this equivalence relation.
Definition A.2. Let N be a fixed
![]() $n\times n$
matrix. We say that an
$n\times n$
matrix. We say that an
![]() $n\times n$
matrix M is N-normal-equivalent if and only if there exists some
$n\times n$
matrix M is N-normal-equivalent if and only if there exists some
![]() $\sigma\in S_n$
such that
$\sigma\in S_n$
such that
![]() $MM^T-M^TM=N_{\sigma}.$
$MM^T-M^TM=N_{\sigma}.$
By definition, it is clear that for any N and for any
![]() $M \sim M'$
, M is N-normal-equivalent if and only if M
′ is N-normal equivalent. On the other hand, as we will see below, one can find a permutation
$M \sim M'$
, M is N-normal-equivalent if and only if M
′ is N-normal equivalent. On the other hand, as we will see below, one can find a permutation
![]() $\rho_{M}$
for any matrix M such that for the matrix
$\rho_{M}$
for any matrix M such that for the matrix
![]() $M'\,:\!=\,M_{\rho_{M}}$
, the ranks of many of the matrices
$M'\,:\!=\,M_{\rho_{M}}$
, the ranks of many of the matrices
![]() $T_k(M'), 1\leq k\leq n$
are large, where
$T_k(M'), 1\leq k\leq n$
are large, where
![]() $T_k(M')$
denotes the matrix from (3.4). Therefore, by Odlyzko’s lemma, we will be able to obtain good upper bounds on the probability of the random matrix
$T_k(M')$
denotes the matrix from (3.4). Therefore, by Odlyzko’s lemma, we will be able to obtain good upper bounds on the probability of the random matrix
![]() $M'\,:\!=\,M_{\rho_M}$
being C-normal, for any fixed C, which then translates to an upper bound on the probability of N-normality of M as follows: for any fixed N,
$M'\,:\!=\,M_{\rho_M}$
being C-normal, for any fixed C, which then translates to an upper bound on the probability of N-normality of M as follows: for any fixed N,
 \begin{eqnarray*}\mathbb{P}\left[M\text{ is }N\text{-normal}\right] & \leq & \mathbb{P}\left[M\text{ is \ensuremath{N}-normal-equivalent}\right]\\[3pt] & = & \mathbb{P}\left[M_{\rho_{M}}\text{ is \ensuremath{N}-normal-equivalent}\right]\\[3pt] & \leq & \sum_{\sigma\in S_{n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is $N_{\sigma}$-normal}\right]\\[3pt] & \leq & n!\sup_{\sigma\in S_{n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is $N_{\sigma}$-normal}\right]\\[3pt] & \leq & 2^{o(n^{2})}\sup_{C\in\mathcal{M}_{n\times n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is \ensuremath{C}-normal}\right],\end{eqnarray*}
\begin{eqnarray*}\mathbb{P}\left[M\text{ is }N\text{-normal}\right] & \leq & \mathbb{P}\left[M\text{ is \ensuremath{N}-normal-equivalent}\right]\\[3pt] & = & \mathbb{P}\left[M_{\rho_{M}}\text{ is \ensuremath{N}-normal-equivalent}\right]\\[3pt] & \leq & \sum_{\sigma\in S_{n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is $N_{\sigma}$-normal}\right]\\[3pt] & \leq & n!\sup_{\sigma\in S_{n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is $N_{\sigma}$-normal}\right]\\[3pt] & \leq & 2^{o(n^{2})}\sup_{C\in\mathcal{M}_{n\times n}}\mathbb{P}\left[M_{\rho_{M}}\text{ is \ensuremath{C}-normal}\right],\end{eqnarray*}
where
![]() $\mathcal{M}_{n\times n}$
denotes the set of all
$\mathcal{M}_{n\times n}$
denotes the set of all
![]() $n\times n$
matrices, and we have used the fact that
$n\times n$
matrices, and we have used the fact that
![]() $n!=2^{o(n^2)}$
. Hence, it suffices to provide a good uniform upper bound on the probability that the random matrix
$n!=2^{o(n^2)}$
. Hence, it suffices to provide a good uniform upper bound on the probability that the random matrix
![]() $M_{\rho_M}$
is N-normal for any fixed N.
$M_{\rho_M}$
is N-normal for any fixed N.
To make the special property of the matrix
![]() $M_{\rho_M}$
precise, we need the following functions, defined for all integers
$M_{\rho_M}$
precise, we need the following functions, defined for all integers
![]() $1\leq s\leq t\leq n$
:
$1\leq s\leq t\leq n$
:
 \begin{equation*}R_{s,t}(i)\,:\!=\,\left\{\begin{array}{c@{\quad}c} i & \text{ if }0<i\leq s\\s &\text{ if }s<i\leq t\\s+t-i &\text{ if }t<i\leq 2n-s-t\\2n-2i & \text{ if }2n-s-t<i\leq n. \end{array}\right.\end{equation*}
\begin{equation*}R_{s,t}(i)\,:\!=\,\left\{\begin{array}{c@{\quad}c} i & \text{ if }0<i\leq s\\s &\text{ if }s<i\leq t\\s+t-i &\text{ if }t<i\leq 2n-s-t\\2n-2i & \text{ if }2n-s-t<i\leq n. \end{array}\right.\end{equation*}
The next proposition is one of the key ideas in the proof of Deneanu and Vu.
Proposition A.3 (Permutation Lemma, Lemma 3.5 in [Reference Deneanu and VuDV19]). Let M be any (fixed)
![]() $n\times n$
matrix. Then, there exist
$n\times n$
matrix. Then, there exist
![]() $s,t\in \mathbb{N}$
and
$s,t\in \mathbb{N}$
and
![]() $\rho_M\in S_n$
such that
$\rho_M\in S_n$
such that
![]() $M_{\rho_M}$
satisfies:
$M_{\rho_M}$
satisfies:
For a fixed matrix N, let
![]() $\mathcal{N}_{s,t}(N)$
denote the set of
$\mathcal{N}_{s,t}(N)$
denote the set of
![]() $\{\pm 1\}$
-valued
$\{\pm 1\}$
-valued
![]() $n\times n$
matrices M such that M is N-normal, and
$n\times n$
matrices M such that M is N-normal, and
![]() $rank(T_i(M)) = R_{s,t}(i)$
for all
$rank(T_i(M)) = R_{s,t}(i)$
for all
![]() $i\in [n]$
. Then, it follows from the previous proposition that
$i\in [n]$
. Then, it follows from the previous proposition that
![]() $M_{\rho_{M}}$
is N-normal if and only if
$M_{\rho_{M}}$
is N-normal if and only if
![]() $M_{\rho_M} \in \bigcup_{1\leq s\leq t\leq n}\mathcal{N}_{s,t}(N)$
. This, in turn, can happen only if M itself is one of the at most
$M_{\rho_M} \in \bigcup_{1\leq s\leq t\leq n}\mathcal{N}_{s,t}(N)$
. This, in turn, can happen only if M itself is one of the at most
![]() $n!\sum_{s,t}|\mathcal{N}_{s,t}(N)|$
matrices obtained by permuting the rows and columns of
$n!\sum_{s,t}|\mathcal{N}_{s,t}(N)|$
matrices obtained by permuting the rows and columns of
![]() $\mathcal{N}_{s,t}(N)$
. Hence, it suffices to provide a good upper bound on
$\mathcal{N}_{s,t}(N)$
. Hence, it suffices to provide a good upper bound on
![]() $|\mathcal{N}_{s,t}(N)|$
uniformly in N, s and t.
$|\mathcal{N}_{s,t}(N)|$
uniformly in N, s and t.
Deneanu and Vu note (Observation 3.7 in [Reference Deneanu and VuDV19]) that
![]() $\mathcal{N}_{s,t}$
is empty unless the following restrictions on s and t are met:
$\mathcal{N}_{s,t}$
is empty unless the following restrictions on s and t are met:
-
•
 $1\leq s \leq 2n/3$
, and
$1\leq s \leq 2n/3$
, and -
•
 $\frac{s}{2} < n-t < s$
.
$\frac{s}{2} < n-t < s$
.
Then, letting
and for some small fixed (but otherwise arbitrary)
![]() $\epsilon > 0$
, letting
$\epsilon > 0$
, letting
they show (Lemmas 5.1 and 5.4 in [Reference Deneanu and VuDV19]) the following:
 \begin{equation}|\mathcal{N}_{s,t}(N)|\leq2^{n^{2}}\times\begin{cases}\min\left(2^{g_{1}(n,s,t)+o(n^{2})},2^{f(\alpha,n,s,t)+o(n^{2})}\right) & s\leq\frac{n}{2}\\[6pt]\min\left(2^{g_{2}(n,k,t)+o(n^{2})},2^{f(\alpha,n,k,t)+o(n^{2})}\right) & s\geq\frac{n}{2}\end{cases},\end{equation}
\begin{equation}|\mathcal{N}_{s,t}(N)|\leq2^{n^{2}}\times\begin{cases}\min\left(2^{g_{1}(n,s,t)+o(n^{2})},2^{f(\alpha,n,s,t)+o(n^{2})}\right) & s\leq\frac{n}{2}\\[6pt]\min\left(2^{g_{2}(n,k,t)+o(n^{2})},2^{f(\alpha,n,k,t)+o(n^{2})}\right) & s\geq\frac{n}{2}\end{cases},\end{equation}
where
 \begin{eqnarray*}f(\alpha,n,s,t) & \,:\!=\, & (1-\alpha)t^{2}-s^{2}/2-n^{2}+ns\\g_{1}(n,s,t) & :\!= & t^{2}-3s^{2}+2sn+st-2nt\\g_{2}(n,s,t) & \,:\!=\, & n^{2}+s^{2}+t^{2}+st-2sn-2nt.\end{eqnarray*}
\begin{eqnarray*}f(\alpha,n,s,t) & \,:\!=\, & (1-\alpha)t^{2}-s^{2}/2-n^{2}+ns\\g_{1}(n,s,t) & :\!= & t^{2}-3s^{2}+2sn+st-2nt\\g_{2}(n,s,t) & \,:\!=\, & n^{2}+s^{2}+t^{2}+st-2sn-2nt.\end{eqnarray*}
Finally, they analyse (A.1) to obtain their bound on
![]() $\beta$
. For this, they note that since for fixed s, both
$\beta$
. For this, they note that since for fixed s, both
![]() $g_1$
and
$g_1$
and
![]() $g_2$
are decreasing functions of t while f is an increasing function of t, and the worst restrictions on
$g_2$
are decreasing functions of t while f is an increasing function of t, and the worst restrictions on
![]() $\beta$
(i.e. those requiring
$\beta$
(i.e. those requiring
![]() $\beta$
to be small) can only be obtained in one of the following six cases:
$\beta$
to be small) can only be obtained in one of the following six cases:
-
(1)
 $t = n-s$
and
$t = n-s$
and
 $s\leq n/2$
, which places the restriction
$s\leq n/2$
, which places the restriction
 $\beta \leq 0.425$
;
$\beta \leq 0.425$
; -
(2)
 $t = n-s/2$
and
$t = n-s/2$
and
 $s \leq n/2$
, which places the restriction
$s \leq n/2$
, which places the restriction
 $\beta \leq 0.307$
;
$\beta \leq 0.307$
; -
(3)
 $t = n-s/2$
and
$t = n-s/2$
and
 $s \geq n/2$
, which places the restriction
$s \geq n/2$
, which places the restriction
 $\beta \leq 0.3125$
;
$\beta \leq 0.3125$
; -
(4)
 $t=s$
and
$t=s$
and
 $s \geq n/2$
, which places the restriction
$s \geq n/2$
, which places the restriction
 $\beta \leq 0.323$
;
$\beta \leq 0.323$
; -
(5)
 $f(\alpha,n,s,t) = g_2(n,s,t)$
and
$f(\alpha,n,s,t) = g_2(n,s,t)$
and
 $s \geq n/2$
, which places the restriction
$s \geq n/2$
, which places the restriction
 $\beta \leq 0.307$
; and finally,
$\beta \leq 0.307$
; and finally, -
(6)
 $f(\alpha,n,s,t) = g_1(n,s,t)$
and
$f(\alpha,n,s,t) = g_1(n,s,t)$
and
 $s \leq n/2$
, which places the worst restriction
$s \leq n/2$
, which places the worst restriction
 $\beta \leq 0.302$
.
$\beta \leq 0.302$
.
Hence, any improvement in Case 6 translates to an overall improvement in their bound. Moreover, note that for
![]() $1\leq s\leq\frac{n}{10}$
, Case 6 only leads to the restriction
$1\leq s\leq\frac{n}{10}$
, Case 6 only leads to the restriction
![]() $\beta\leq0.7$
. Therefore, it suffices to improve Case 6 for
$\beta\leq0.7$
. Therefore, it suffices to improve Case 6 for
![]() $\frac{n}{10}\leq s\leq\frac{n}{2}$
. We will do this using Proposition 3.8.
$\frac{n}{10}\leq s\leq\frac{n}{2}$
. We will do this using Proposition 3.8.
We start by showing how to deduce the upper bound
![]() $g_{1}(n,s,t)$
, as in [Reference Deneanu and VuDV19]. For any
$g_{1}(n,s,t)$
, as in [Reference Deneanu and VuDV19]. For any
![]() $0\leq k\leq n$
, we define
$0\leq k\leq n$
, we define
where recall that
![]() $\mathcal{P}_{k}$
denotes the set of k-partial matrices, and
$\mathcal{P}_{k}$
denotes the set of k-partial matrices, and
![]() $M_{k}$
denotes the k-partial matrix associated to M. By definition, the number of ways to extend any k-partial matrix in
$M_{k}$
denotes the k-partial matrix associated to M. By definition, the number of ways to extend any k-partial matrix in
![]() $\mathcal{S}_{k,(s,t)}(N)$
to a
$\mathcal{S}_{k,(s,t)}(N)$
to a
![]() $(k+1)$
-partial matrix in
$(k+1)$
-partial matrix in
![]() $\mathcal{S}_{k+1,(s,t)}(N)$
is at most the number of
$\mathcal{S}_{k+1,(s,t)}(N)$
is at most the number of
![]() $\{\pm1\}$
-valued solutions to :
$\{\pm1\}$
-valued solutions to :
![]() $T_{k}x_{k}=N^{\prime}_{k}$
, which is at most
$T_{k}x_{k}=N^{\prime}_{k}$
, which is at most
![]() $2^{\max\{2(n-k-1)-rank(T_{k}),0\}}$
by Odlyzko’s lemma (Lemma 1.4). Hence, it follows that the total number of matrices in
$2^{\max\{2(n-k-1)-rank(T_{k}),0\}}$
by Odlyzko’s lemma (Lemma 1.4). Hence, it follows that the total number of matrices in
![]() $\mathcal{N}_{s,t}(N)$
is at most
$\mathcal{N}_{s,t}(N)$
is at most
 \begin{eqnarray*}|\mathcal{N}_{s,t}(N)| & \leq & 2^{o(n^{2})}\prod_{k=0}^{n}2^{\max\{2(n-k-1)-rank(T_{k}),0\}}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{n}2^{\max\{2(n-k)-R_{s,t}(i),0\}}\\ & = & 2^{g_{1}(n,s,t)+o(n^{2})},\end{eqnarray*}
\begin{eqnarray*}|\mathcal{N}_{s,t}(N)| & \leq & 2^{o(n^{2})}\prod_{k=0}^{n}2^{\max\{2(n-k-1)-rank(T_{k}),0\}}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{n}2^{\max\{2(n-k)-R_{s,t}(i),0\}}\\ & = & 2^{g_{1}(n,s,t)+o(n^{2})},\end{eqnarray*}
where the second equality follows from the definition of
![]() $\mathcal{N}_{s,t}(N)$
and the last equality follows by direct computation.
$\mathcal{N}_{s,t}(N)$
and the last equality follows by direct computation.
To obtain our improvement, we note that above computation may be viewed in the following two steps:
-
•
 $|\mathcal{N}_{s,t}(N)| \leq 2^{o(n^{2})}|\mathcal{S}_{\beta n,(s,t)}(N)|\prod_{k=\beta n+1}^{n}2^{\max\{2(n-k-1)-\textrm{rank}(T_{k}),0\}}$
, which is true for any
$|\mathcal{N}_{s,t}(N)| \leq 2^{o(n^{2})}|\mathcal{S}_{\beta n,(s,t)}(N)|\prod_{k=\beta n+1}^{n}2^{\max\{2(n-k-1)-\textrm{rank}(T_{k}),0\}}$
, which is true for any
 $0< \beta < 1$
$0< \beta < 1$
-
• For
 $0< \beta < 1$
such that
$0< \beta < 1$
such that
 $\beta n < s$
, In particular, by our assumption on s, we know that this holds for (say)
$\beta n < s$
, In particular, by our assumption on s, we know that this holds for (say) \begin{eqnarray*}|\mathcal{S}_{\beta n,(s,t)}(N)| & \leq & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{\max\{2(n-k-1)-\textrm{rank}(T_{k}),0\}}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{2(n-k)-\textrm{rank}(T_{k})}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{2n-3k}\\ & = & 2^{(2\beta-\beta^{2})n^{2}-\beta^{2}n^{2}/2+o(n^{2})}\end{eqnarray*}
\begin{eqnarray*}|\mathcal{S}_{\beta n,(s,t)}(N)| & \leq & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{\max\{2(n-k-1)-\textrm{rank}(T_{k}),0\}}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{2(n-k)-\textrm{rank}(T_{k})}\\ & = & 2^{o(n^{2})}\prod_{k=0}^{\beta n}2^{2n-3k}\\ & = & 2^{(2\beta-\beta^{2})n^{2}-\beta^{2}n^{2}/2+o(n^{2})}\end{eqnarray*}
 $\beta = 2^{-10}$
.
$\beta = 2^{-10}$
.
However, by Proposition 3.8 and Section 3.3, we already know that for
![]() $\beta = 2^{-10}$
,
$\beta = 2^{-10}$
,
Using this improved bound in the previous computation, we get that
![]() $|\mathcal{N}_{s,t}(N)|\leq2^{h(n,s,t)+o(n^{2})}$
, where
$|\mathcal{N}_{s,t}(N)|\leq2^{h(n,s,t)+o(n^{2})}$
, where
Hence, we have showed that Case 6 can be replaced by the following two cases:
Case 6.1
![]() $f(\alpha,n,s,t) = g_1(n,s,t)$
and
$f(\alpha,n,s,t) = g_1(n,s,t)$
and
![]() $s\leq n/10$
$s\leq n/10$
Case 6.2
![]() $f(\alpha,n,s,t) = h(n,s,t)$
and
$f(\alpha,n,s,t) = h(n,s,t)$
and
![]() $n/10 \leq s \leq n/2$
,
$n/10 \leq s \leq n/2$
,
each of which place a restriction on
![]() $\beta$
which must be larger than the constant
$\beta$
which must be larger than the constant
![]() $c_{DV}$
obtained in [Reference Deneanu and VuDV19]. This completes the proof of Theorem 1.15.
$c_{DV}$
obtained in [Reference Deneanu and VuDV19]. This completes the proof of Theorem 1.15.