Early investigation of Pólya urns considered drawing balls one at a time. In the last two decades, several authors have considered multiple drawing in each step, but mostly for schemes involving two colors. In this manuscript, we consider multiple drawing from urns of balls of multiple colors, formulating asymptotic theory for specific urn classes and addressing more applications. The class we consider is affine and tenable, built around a ‘core’ square matrix. We examine cases where the urn is irreducible and demonstrate its relationship to matrix irreducibility for its core matrix, with examples provided. An index for the drawing schema is derived from the eigenvalues of the core. We identify three regimes: small, critical, and large index. In the small-index regime, we find an asymptotic Gaussian law. In the critical-index regime, we also find an asymptotic Gaussian law, albeit with a difference in the scale factor, which involves logarithmic terms. In both of these regimes, we have explicit forms for the structure of the mean and the covariance matrix of the composition vector (both exact and asymptotic). In all three regimes we have strong laws.

We study fluctuations of the error term for the number of integer lattice points lying inside a three-dimensional Cygan–Korányi ball of large radius. We prove that the error term, suitably normalized, has a limiting value distribution which is absolutely continuous, and we provide estimates for the decay rate of the corresponding density on the real line. In addition, we establish the existence of all moments for the normalized error term, and we prove that these are given by the moments of the corresponding density.

The aim of the paper is to derive the distribution of the number of retrial of the tagged request and as a consequence to present the waiting time analysis of a finite-source M/M/1 retrial queueing system by using the method of asymptotic analysis under the condition of the unlimited growing number of sources. As a result of the investigation, it is shown that the asymptotic distribution of the number of retrials of the tagged customer in the orbit is geometric with given parameter, and the waiting time of the tagged customer has a generalized exponential distribution. For the considered retrial queuing system numerical and simulation software packages are also developed. With the help of several sample examples the accuracy and range of applicability of the asymptotic results in prelimit situation are illustrated showing the effectiveness of the proposed approximation.

We study an urn model introduced in the paper of Chen and Wei (2005), where at each discrete time step m balls are drawn at random from the urn containing colors white and black. Balls are added to the urn according to the inspected colors, generalizing the well known Pólya-Eggenberger urn model, case m = 1. We provide exact expressions for the expectation and the variance of the number of white balls after n draws, and determine the structure of higher moments. Moreover, we discuss extensions to more than two colors. Furthermore, we introduce and discuss a new urn model where the sampling of the m balls is carried out in a step-by-step fashion, and also introduce a generalized Friedman's urn model.

The conditional least-squares estimators of the variances are studied for a critical branching process with immigration that allows the offspring distributions to have infinite fourth moments. We derive different forms of limiting distributions for these estimators when the offspring distributions have regularly varying tails with index α. In particular, in the case in which 2 < α < 8/3, the normalizing factor of the estimator for the offspring variance is smaller than √n, which is different from that of Winnicki (1991).

Two methods for approximating the limiting distribution of the present value of the benefits of a portfolio of identical endowment insurance contracts are suggested. The model used assumes that both future lifetimes and interest rates are random. The first method is similar to the one presented in Parker (1994b). The second method is based on the relationship between temporary and endowment insurance contracts.

We study certain stochastic processes arising in probabilistic modelling. We discuss the limit behavior of these processes and estimate the rate of convergence to the limit.

Let be a sequence of independent and identically distributed random vectors drawn from the d-dimensional unit ball Bd and let Xn be the random polytope generated as the convex hull of a1,· ··, an. Furthermore, let Δ(Xn): = Vol (BdXn) be the volume of the part of the ball lying outside the random polytope. For uniformly distributed ai and 2 we prove that the limiting distribution of Δ(Xn)/Ε (Δ (Xn)) for n → ∞ (satisfies a 0–1 law. In particular, we show that Var for n → ∞. We provide analogous results for spherically symmetric distributions in Bd with regularly varying tail. In addition, we indicate similar results for the surface area and the number of facets of Xn.

An approximation of the distribution of the present value of the benefits of a portfolio of temporary insurance contracts is suggested for the case where the size of the portfolio tends to infinity. The model used is the one presented in Parker (1922b) and involves random interest rates and future lifetimes. Some justifications of the approximation are given. Illustrations for limiting portfolios of temporary insurance contracts are presented for an assumed Ornstein-Uhlenbeck process for the force of interest.

In this paper, we consider kth-order two-state Markov chains {Xi} with stationary transition probabilities. For k = 1, we construct in detail an upper bound for the total variation d(Sn, Y) = Σx |𝐏(Sn = x) − 𝐏(Y = x)|, where Sn = X1 + · ··+ Xn and Y is a compound Poisson random variable. We also show that, under certain conditions, d(Sn, Y) converges to 0 as n tends to ∞. For k = 2, the corresponding results are given without derivation. For general k ≧ 3, a conjecture is proposed.

This paper is concerned with the rate of convergence of certain functionals associated with a stochastic process arising in the modelling of soil erosion. Some limit theorems are derived for the total crop production Sn over a number n of years, and the rate of convergence of Sn to its limit S is discussed. Some stability assumptions are considered, and particular stable geometric infinitely divisible processes analyzed.

A wide class of multichannel queueing models appears to be useful in practice where the input stream of customers can be controlled at the moments preceding the customers' departures from the source (e.g. airports, transportation systems, inventories, tandem queues). In addition, the servicing facility can govern the intensity of the servicing process that further improves flexibility of the system. In such a multichannel queue with infinite waiting room the queueing process {Zt; t ≧ 0} is under investigation. The author obtains explicit formulas for the limiting distribution of (Zt) partly using an approach developed in previous work and based on the theory of semi-regenerative processes. Among other results the limiting distributions of the actual and virtual waiting time are derived. The input stream (which is not recurrent) is investigated, and distribution of the residual time from t to the next arrival is obtained. The author also treats a Markov chain embedded in (Zt) and gives a necessary and sufficient condition for its existence. Under this condition the invariant probability measure is derived.

Let N(t) be a birth-death process on 𝒩= {0, 1, 2, ·· ·} governed by the transition rates λn > 0 (n ≧ 0) and μn > 0 (n ≧ 1) where λn → λ > 0 and μn → μ > 0 as n → ∞ and ρ = λ/μ. Let Tmn be the first-passage time of N(t) from m to n and define It is shown that, when converges in distribution to TBP(μ,λ) as n → ∞ where TΒΡ (μ,λ) is the server busy period of an M/M/1 queueing system with arrival rate μ and service rate λ. Correspondingly T0n/E[T0n] converges to 1 with probability 1 as n →∞. Of related interest is the conditional first-passage time mTrn of N(t) from r to n given no visit to m where m < r < n. As we shall see, the conditional first-passage time of N(t) can be viewed as an ordinary first-passage time of a modified birth-death process M(t) governed by where are generated from λn and μn. Furthermore it is shown that for and while for and This enables one to establish the relation between the limiting behavior of the ordinary first-passage times and that of the conditional first-passage times.

Let 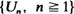be i.i.d. uniform on (0,1) random variables and define Si,n = Ui,n–1Ui–1,n–1, i = 1, · ··, n where the Ui–n–1 are the order statistics from a sample of size n – 1 and U0,n–1 =0 and Un,n–1 = 1. The Si,n are called the spacings divided by U1,· ··,Un–1. For a fixed integer l, set 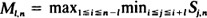. Exact and weak limit results are obtained for the Ml,n. Further we show that with probability 1 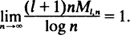This extends results of Cheng.

Let ℰ be an event governed by a homogeneous second-order two-state Markov chain. Assume the steady state has been achieved. Consider Nm the number of times that ℰ occurs in m successive trials. The limiting distribution of P(Nm = k) is obtained under the condition that mP(ℰ)=λ.

Let X1X2, · ·· be a Markov Bernoulli sequence with initial probabilities p of success and q = 1 – p of failure, and probabilities 1 – (1 – π) p, (1 – π) p in the first row and (1 – π) (1 – p), (1 – π) p + πin the second row of the transition matrix. If we define Sn = Σi=1nXi, then the limit distribution P{Sn = k} is obtained when n →∞, np →λ.

Consider an array of binary random variables distributed over an m1(n) by m2(n) rectangular lattice and let Y1(n) denote the number of pairs of variables d, units apart and both equal to 1. We show that if the binary variables are independent and identically distributed, then under certain conditions Y(n) = (Y1(n), · ··, Yr(n)) is asymptotically multivariate normal for n large and r finite. This result is extended to versions of a model which provide clustering (repulsion) alternatives to randomness and have clustering (repulsion) parameter values nearly equal to 0. Statistical applications of these results are discussed.

In this article we give limiting results for arrays {Xij (m, n) (i, j) Dmn} of binary random variables distributed as particular types of Markov random fields over m x n rectangular lattices Dmn. Under some sparseness conditions which restrict the number of Xij (m, n)'s which are equal to one we show that the random variables (l = 1, ···, r) converge to independent Poisson random variables for 0 < d1 < d2 < · ·· < dr when m→∞ nd∞. The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.

Two independent i.i.d. sequences of random variables {Un} and {Dn} generate a Markov process {Xn} by Xn = max(Xn–1 – Dn, Un), n = 1, 2, …. ‘Exchange’ is defined as the event [Un > Xn–1 – Dn]. Conditions for existence of a limiting distribution for {Xn} are established, and normalization is discussed when no limiting distribution exists. Finally the process {Xn at the k th exchange; k = l, 2, …} and the time between consecutive exchanges are considered.

A discrete-time Markov process on the interval [0, 1] is considered. Sufficient conditions for the existence of a unique stationary limiting distribution are given.